“有趣的进制”课堂教学实录与评析

【教学内容】

西南师大版《数学文化读本》四年级上册“有趣的进制”。

【教学过程】

一 小魔术引入

师：我有一个特异功能，能看到大家心里想的是什么，你们信吗？

生：不信。

师：不信？咱们现在就来试试。这里有15张扑克牌（出示红桃 A、2、3、…、K 和大王、小王），请你选一张牌但不要说出来。看着图1回答我几个问题，我就能知道你选的是哪张牌。

图1

生：第1幅有，第2幅没有，第3幅没有，第4幅有。

师：红桃9。

生：您是怎么知道的？

师：怎样？这下大家相信了吧！奇怪吗？

生：奇怪。

师：大家想知道我是怎么做到的吗？这节课我们就来揭秘。

评析：利用扑克猜数游戏引入，激起学生的好奇心理，激发学生的探究欲望和学习兴趣，学生急切地想知道：老师是怎么做到的呢？同时，让学生逐渐体会科学探索的方式。

二十进制回顾

师：（出示十进制计数器）你能在计数器上从1拨到10吗？

学生在计数器上演示：1、2、3、4、5、6、7、8、9、10。

师：为什么10可以用十位上的1个珠子表示呢？

生：满十要向前一位进1，十位上的1表示1个十。

师：计数器是按满十进1的方法进行计数的，这样的计数法叫作十进制计数法。

评析：认识二进制、十进制是一个重要的基础。因此，课始借助多媒体演示满十进1，回顾十进制计数法，为学生运用迁移规律认识二进制打好基础。

三二进制试学

师：在计数器上拨珠子你会吗？老师这里有一个计数器，（出示二进制计数器）谁愿意上来拨一拨？

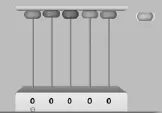
图2

1.在只有1个珠子的计数器上拨1，再拨2。

学生拨出1后，拨不出2。

师：怎么不拨了呀？在这样的计数器上能表示2吗？

生1：把计数器打开，再添上几个珠子。

师：就这个计数器，不能搞破坏。

学生表示不能。教师播放视频，演示十进制和二进制的来源和特点。

师：观看了这个视频后，在这个计数器上能拨出2吗？

生：如果是满十进1的话，在这个计数器上是拨不出2的，但如果是满二进1的话，应该可以。

生：1+1=2，满二向前一位进1。

……

2.像这样按照满二进1的原则进行计数的方法，人们把它叫作二进制计数法。

师：按照二进制计数法，2用数怎么表示？

生：10。

师：这个代表1个“十”吗？

生：不表示1个“十”，只表示1个“二”。

师：所以这里不能读十，要读一零。我们回忆一下，十进制计数法是由哪几个数字组成的？

生：1、2、3、4、5、6、7、8、9。

生：还有0，共10个数字。

师：那么二进制计数法由几个数字组成呢？

生：2个。

生：由0和1组成。

师：二进制里面能出现2吗？

生：不能，二进制里面只能出现0和1。

评析：教师特制了每档只有一个珠子的计数器，巧用学具，让学生在特制的计数器上拨出2，制造认知冲突，激发了学生的探究欲望和学习兴趣。通过动画视频让学生了解了二进制的来历及“满二进1”的计数原则，巧妙地让学生自己学习，解决问题，增强了求知欲望。

四 师生共学

师生一起用二进制表示3、4。

师：如果还是满二进1，3该怎么表示呢？

生：100。

生：11。

师：现在出现了两种不同的意见，到底哪种对呢？在计数器上拨一拨3，验证一下，并说一说你是怎么想的。

生：（边拨边说）只要在2的基础上再加1就是3了，所以是11而不是100。

生：第2档上的1个珠子表示1个“二”，第1档上的1个珠子表示1个“一”，合起来就表示3。所以用11表示3，而不能用100表示。

师：大家同意吗？

生：同意。

师：4怎么表示呢？自己先想一想，同桌之间再互相讨论一下。

生：3+1=4，第一档上加1满二就向前一位进1，变成20。因为二进制里面不能出现2，所以第二档上满二也向前一位进1，变成100，表示4。

生：还可以用竖式表示3+1=4，3是11，加1就是右起第一位1+1=2，满二进1，该位写0；第二位 1加上进上来的1，又变成2了，满二再向前一位进1，这一位写0得到100。

……

师：没有珠子记作0，1个珠子我们记作1，2就可以用10来表示……（先利用计数器演示：从1拨到4，再用竖式演示1+1=10,2+1=11,3+1=100）

评析：动手操作，师生共同用二进制计数法表示3和4，通过计数器和竖式演示，深化学生对满二进1的理解。

五 合作探究

用二进制计数法表示 5、6、7、8。

师：刚才我们一起用二进制计数法表示出2、3、4，接下来是 5、6、7、8，你能用二进制计数法表示出这些数吗？老师给每个小组准备了一个这样的计数器，大家来试一试，并用二进制计数法表示出来。

出示小组合作要求：

1.在小组长的组织下，在计数器上拨一拨；

2.在学习任务单上填一填；

3.用竖式检验一下对不对；

4.准备汇报。

……

评析：动手操作，建立丰富的表象，是学生认识二进制的重要途径。这里设计了三个层次的活动：第一个层次，师生共拨珠子表示3和4，通过计数器和竖式的演示，深化学生对“满二进1”的理解；第二个层次，学生独立拨珠子表示5、6、7、8，积累更多感性认识；第三个层次，学生在操作中思考怎样快速用二进制计数法表示。这样由扶到放的设计，让学生的探究活动变得更有成效。

六 巩固揭秘

1.练一练：用二进制计数法写出这些扑克牌的位置。（如图3）

生：第9张牌用二进制计数法表示是1001。

生：第10张牌用二进制计数法表示是1010。

……

2.让学生揭秘猜扑克游戏。

师：结合图3，看图1中的第1幅图，扣过去的扑克牌有什么特点？什么样的扑克牌扣过去了，什么样的扑克牌还在？

图3

生：个位是0的扑克牌扣过去了，个位是1的扑克牌还在。

师：我问大家在这幅图中某张扑克牌扣过去没有，其实就是让大家告诉我什么？

生：这张牌在图中位置顺序号的个位是0还是1。

师：图1中第2幅图呢？

生：这幅图的特点是从右数往左第二位是0的扑克牌扣过去了，是1的扑克牌还在。

生：在不在说明从右数往左第二位是0还是1。

生：第3幅图的特点是从右往左数第三位是0的扑克牌扣过去了，是1的扑克牌还在。

生：在不在说明从右往左数第三位是0还是1。

生：第4幅图的特点是从右往左数第四位是0的扑克牌扣过去了，是1的扑克牌还在。在不在说明从右往左数第四位是0还是1。

生：这些扑克牌的顺序号只有四位数，问我们四次，其实就是让我们把这个四位数告诉你了。

生：哇，原来是这样哦。

师：那我选一张牌，大家能猜出来吗？

生：（齐声）能。

师：第1幅没有，第2幅没有，第3幅有，第4幅有。

生：红桃Q。

评析：练习的设计，一方面让学生进行简单的十进制到二进制的转化，以及二进制的计算等基本的练习；另一方面，揭秘猜扑克游戏，使学生知道生活中处处有数学，学生学习数学的热情高涨。

七拓展延伸

1.生活中你见过二进制吗？

师：通过动画演示，我们知道计算机采用的是什么进制。

2.介绍太极八卦，感受国学的博大精深。

师：（出示八卦图）这上面有二进制吗？如果把“―”看作数字“1”，“――”看作数字“0”，那么乾卦就可以看成“111”，表示7。其他的呢？

师：古老的太极八卦图里也蕴藏着二进制。你感觉怎么样？

师：这么伟大的二进制是谁发明的呢？17世纪德国数理哲学大师莱布尼茨受八卦的阴爻“— —”和阳爻“—”启发而发明了二进制，所以中国也可以说是二进制的故乡。

3.介绍钟表里面的十二进制、六十进制。

师：其实除了这些进制，生活中还有很多进制，如八进制、十六进制、二十四进制等。

4.总结并介绍学习数学文化的目的，即启迪思维，激发灵感，应用创造。（略）

评析：通过古老的八卦与现代的钟表及二进制在现代科技生活中的广泛运用，让学生看到数学世界穿越时空的神奇与博大，感受到数学的力量，感受到数学学习的恒久魅力。