如何给小学生上一节“分形”的课
【教学内容】
西南师大版《数学文化读本》四年级下册“科克雪花”。
【教学过程】
一、提问引入,驱动探究任务
师:(板书:科克雪花)看到这个标题,你会有什么疑问?
生:为什么叫“科克雪花”?
生:和我们平时所说的雪花一样吗?
生:科克雪花有什么特点呢?
师:科克雪花是1904年由瑞典数学家科克受雪花形状的启发创造出来的,因此就以他的名字命名。
评析:学生看到“科克雪花”这个标题就会有很多疑问,先让他们说说自己的问题,一方面可激发学习兴趣,另一方面在问题驱动下教学也会更加有效。
二、探讨画法,初步感知特点
师:先来看看它是怎么创造出来的。这个图形有点儿复杂,怎么办?我们把它简化一下,先画一个等边三角形。在脑子里想象一下,“科克雪花”是怎样从三角形一步一步演变过来的?
生1:可再画一个等边三角形,进行旋转,把两个三角形叠放到一起。
生2:还可以把等边三角形的一条边进行三等分,再从中间那里画一个等边三角形。
师:好,我们用动画演示一下。(如图1)
生:接下来重复生2的步骤,重复几次就能得到“科克雪花”了。

图1
评析:将“科克雪花”画法的教学分成了三步。第一步是“简化”,通过简化,演变到学生熟悉的等边三角形;第二步是“想象画”,探讨“科克雪花”是怎样从等边三角形演变过来的,给学生充分的想象空间;第三步讨论“科克雪花”的“具体画法”,学生充分感受到了“科克雪花”是“不断重复性”的操作结果。
三、探究特征,发现变化规律
师:从左往右仔细观察图1,从第1幅到第4幅,发生了什么变化?
生:它们的边长、周长、面积都发生了变化。(教师板书)
(一)探索边数特征。
1.学生自主数。
师:先来看看边数发生了什么变化。同学们拿出学习单,数一数,填一填。(如图2)
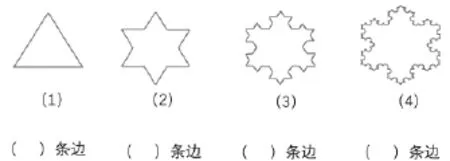
图2
2.学生汇报。(略)
3.发现规律。
生:我其实没有数,我是发现了边数之间的规律,都是乘4的关系。
师:你是怎么发现这个规律的?
(1)方法一:数一数。
生:我先数出前面几个图形的边数,再推测出第4个图形的边数是48×4=192。
(2)方法二:根据边数的变化规律。
生:三角形的每条边都变成了4条边。(教师动态演示)
生:所以第2个图形有3×4条边,第3个图形有 3×4×4 条边,第 4 个图形就有 3×4×4×4=192(条)边。
师:第10个图形有几条边呢?

师:(小结)每变化一次,边数就变为原来的4倍。
(二)探索周长特征。
1.学生自主算。
师:它的周长又会怎么变呢?假设等边三角形的边长为9,数一数,算一算。
2.学生汇报。
(1)方法一:根据边长×边数。
生:算出每条边的长度,乘上边数就可以了。
师:边数我们刚才已经研究过了,再看边长是怎么变化的。(教师动态演示,如图3)
师:我们再计算出它们的周长。

图3
(2)方法二:根据周长的变化规律。
生:前面图形的每条边都平均分成3份,到后面的图形就变成了4份,相当于每条边的长度都增加了,周长也就增加了,所以后一个图形的周长就是前一个图形周长的倍。如图4

图4
师:第10个图形的周长是多少?
师:如果一直变下去,周长会变成无限大吗?
学生思考,并进行辩论,最后得出结论:周长会变成无限大。
(三)探索面积特征。
师:一直这样变下去,它的面积会变成无限大吗?
生:会,因为面积一直在变大,最后就会变成无限大。
生:不会,因为面积增加的部分越来越小了。
学生开始争辩,教师出示原三角形的外接圆。(如图 5)

图5
生:一定会比它的外接圆面积小,面积不会变成无限大。
评析:学生在探究的过程中发现了边数、边长、周长的变化规律。其中周长的变化规律是最难理解的。大部分学生是利用边数×边长的方法,也有部分学生是利用周长的变化特征来解决的。教师追问第10个图形的边数、周长,让学生明白“科克雪花”是按照一定的规律一直变化下去的。
四、欣赏分形,感受数学之美
师:你相信有这样的曲线吗?它所围的面积是有限的,但它的周长趋于无穷大!
生:有,“科克雪花”曲线就是这样的。(教师动态演示)
师:你相信有这样的平面图形吗?它的周长趋于无穷大,但它的面积趋于零。(学生沉默)有,谢尔宾斯基三角形就是这样的。(动态演示,如图6)

图6
师:你相信有这样的立体图形吗?它的表面积趋于无穷大,而它的体积趋于零。(学生沉默)有,门格尔海绵就是这样的。(动态演示,如图7)

图7
师:这三个图形人称几何中的三大怪物,它们都是“分形”。
师:你觉得什么是“分形”?
生:重复前面的操作。
生:不管放大多少倍,都是长一样的。
生:它们的规律都是一样的。
师:下面请同学们欣赏分形图形。(出示各种动态图)分形也称为大自然的几何。
评析:通过对“几何三大怪物”的欣赏,打破学生的几何思维,最后引出像这样的图形就是 “分形”。接下来欣赏各种分形的动态图和大自然中分形的景象。让学生在欣赏中感受分形之美,感受数学之美,激发学生进一步探索、研究数学。
五、总结提升,增强数学情感
师:分形为人们从局部认识整体、从有限认识无限提供了方法。它让我们对几何的研究进入了一个新的世界,这个世界等待着同学们去探索。
【总评】
对四年级学生来说,对“科克雪花”特征的探究还存在很大的难度,也无法更进一步感受“分形”的美妙。于是这节课唐老师在六年级进行教学尝试。整节课从画“科克雪花”再到对其特征的探索,再到分形的介绍和赏析,让学生一步步感知分形。

