绳系系统轨道机动过程中的面内摆角抑制*

薛 超，谈树萍,2,刘贺龙

(1.北京控制工程研究所,北京 100090; 2.空间智能控制技术国家级重点实验室,北京 100190)



绳系系统轨道机动过程中的面内摆角抑制*

薛 超1，谈树萍1,2,刘贺龙1

(1.北京控制工程研究所,北京 100090; 2.空间智能控制技术国家级重点实验室,北京 100190)

针对绳系卫星系统轨道机动过程中面内摆角抑制问题进行控制器设计.仅考虑面内摆角子系统下，针对绳系系统的动力学模型，提出了分层迭代非线性滑模控制方法.证明控制方法设计的控制律使系统所有状态渐近稳定.通过数学仿真验证方法的有效性和优势.

绳系卫星系统;滑模控制;轨道机动

0 引 言

绳系卫星系统(tethered satellite system,TSS)在深空探测、空间碎片移除和系绳辅助航天器再入等方面应用广泛，成为国内外研究的热点[1].目前对绳系系统的研究大多集中在特定轨道下绳系系统的构型稳定及抖振抑制问题，很少涉及绳系系统的轨道机动问题，然而随着技术及工程应用研究的不断深入，利用绳系远程交会、在轨操控等问题都必须考虑绳系系统机动问题，绳系组合体拖曳离轨问题也逐渐成为研究人员的研究热点[2-10].

针对绳系系统离轨的策略问题，Liu等[2-4]针对大型空间碎片提出了由加速、平衡、旋转和返回构成的4个阶段绳系拖曳离轨方案.王道吉[5]指出静止轨道高度上绳系组合体离轨拖曳过程中转移段单纯采用重力梯度策略无法保证离轨拖曳过程的安全，进而研究了开关推力器拖曳离轨策略和组合电拖进策略，通过能量分析发现这两种策略存在很大的优化空间.Lee等[6]提出了输入成形推力机动策略，能有助于绳系系统达到仅受重力梯度影响的平稳振动状态并减少了两星碰撞的可能性.但这些研究都只是定性地研究出离轨方案，并没有点出离轨过程中系统的稳定性及其平衡点等问题.

孙亮等[7-8]进一步对绳系系统离轨系统稳定和控制性能进行研究，提出了非开普勒轨道下的绳系系统动力学模型，并对模型的平衡点及各工况下的系统稳定性进行研究，同时采用分层滑模的控制方法使绳系系统在轨道机动过程中构型稳定.Liu等[10]进一步提出了高阶滑模控制器并研究了系统状态的边界条件.然而绳系系统控制输入为系绳张力，存在张力需大于零的控制约束，在系统初值改变情况下很容易不满足控制约束.

本文基于孙亮等[7-8]提出的动力学模型设计了分层迭代非线性滑模控制方法，并详细证明控制方法的稳定性，在设计迭代过程中，对系统各个信号约束限幅，从而改善控制过程的动态特性.

1 动力学模型

拖曳离轨绳系系统，由任务星、目标星以及连接两星之间的系绳组成，可用哑铃模型来描述，如图1所示.

图1 轨道系与系统姿态关系图Fig.1 Orbital and attitude coordinate system

任务星质量为M，目标星质量为m，任务星和目标星之间的绳长为lT，则系统质心到目标星间的绳长l=lTM/(M+m)，任务星在推力大小F的作用牵引非合作目标运动，绳系系统质心O的升交点赤经、轨道倾角及轨道幅角分别为Ω、i和u.并作出如下假设：
假设1.假设任务星和目标星为刚体，并将任务星和目标星均视为质点，暂时不考虑非球形引力、气动力和太阳光压等摄动力的影响;
假设2.系绳张力大于零时系绳可视为无拉伸、无压缩和无弯曲变形的理想直杆，不考虑其质量和阻尼特性，且直杆长度可变[9].

根据欧拉-拉格朗日方程可以得出绳系系统的动力学模型为

(1)

(2)

(3)

其中，T为系绳张力大小，r为轨道矢径大小，l为系绳绳长长度，θ，φ分别为系统面内外摆角，L为轨道坐标系到地心坐标系的转换矩阵，S为星体在赤道惯性坐标系下的位置向量，所涉及的参量都由质心轨道运动所决定，矩阵L和向量S同文献[7]中给出，μ为地球引力常数.

施加在任务星上的推力加速度与系统质心运动有关，且推力方向可调节. 在任务星的牵引下，绳系系统质心受到的推力加速度大小f=F/(M+m)，其分量如图2所示.径向分量fr沿矢径方向，如图方向为正；横向分量fu在轨道平面内垂直于矢径，沿轨道幅角u增大的方向为正，副法向分量fh垂直于轨道平面，沿轨道面正方向，本文重点研究面内摆角抑制，即假设副法向分量fh已使面外摆角稳定.

图2 加速度各分量的描述图Fig.2 The components of trust acceleration

2 分层迭代非线性滑模控制律设计

绳系系统面内摆角属于典型的欠驱动控制系统.令l=(1+εl)lc,θ=θc+εθ，lc为固定的期望绳长，θc为期望的面内摆角，l,θ为实际的绳长和面内摆角，则可将系统动力学写成如下控制模型[7]：

(4)

其中，

3μr-3cos2(θc+x3)-μr-3]-

3μr-3sin(θc+x3)cos(θc+x3)-

x1∈[lmin-l0,lmax-l0]，l0,lmin,lmax分别为系绳原长，系绳最小长度及系绳最大长度，U为系绳张力.

绳系系统轨道机动过程中面内外摆角的期望值如下[7]:

(5)

将系统(4)拆分成两个子系统考虑

(6)

(7)

设计非线性滑模面如下:

(8)

(9)

其中，ci>0(i=1,2,3,4).

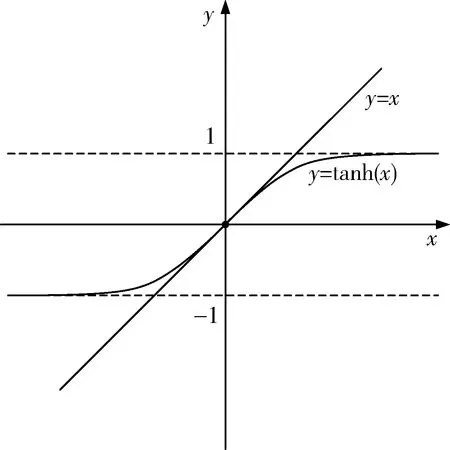
图3 非线性函数双曲正切曲线特性Fig.3 Curve characteristic of hyperbolic tangent function

(10)

结合式(6)、(8)和(10)，则控制律为

(11)

(12)

其中，假设Ueq1与Ueq2中的bi≠0(i=1,2)，定义滑模面

s=cstanh(ασ2+βσ4)

(13)

其中，α,β>0.定义Lyapunov函数

(14)

则其导数为

(15)

设计控制律

U=Ueq1+Ueq2+Usw

(16)

结合式(8)、(9)、(11)、(12)、(15)、(16)有

(17)

则可设计转换控制律

(18)

其中，λ,η>0.将(18)代入(17)有

(19)

即滑模面(13)渐近稳定，则实际分层迭代非线性滑模控制律有

U=Ueq1+Ueq2+Usw

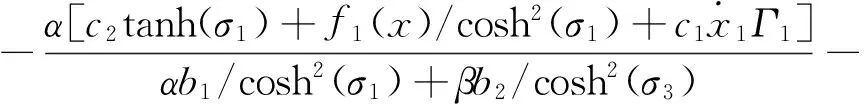
(20)

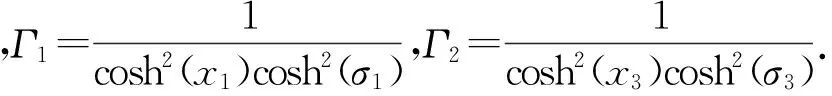
(21)

定理1.考虑单输入多输出系统(4)，设计如(13)滑模面，选取如(21)控制律，同时所涉及的控制参数均选取大于零常数，则系统(4)中所有状态都是渐近稳定的.

证明.

定义如下变量和Lyapunov函数

s1=ασ2+βσ4

(22)

(23)

则在控制律(21)下Lyapunov函数V1的导数为

=-λcss1tanh(s1)-ηs1tanh(cstanh(s1))≤0

(24)

即变量s1和Lyapunov函数V1皆渐近稳定，则有

(25)

结合式(24)、(25)及双曲正切函数特性可知

(26)

进一步有

(27)

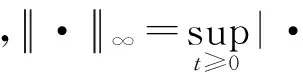
(28)

(29)

结合式(26)、(29)可得

(30)

根据连续变量s1的渐近稳定性，进一步有

(31)

由于参数α,β为定常数不影响变量s1稳定性，则可以构建如下两个不同定常参数组成的连续变量s1

s1,1=α1σ2+βσ4

(32)

s1,2=α2σ2+βσ4

(33)

其中，α1≠α2.不妨假设

(34)

则

(35)

进一步可得

(36)

式(36)可改写为

(37)

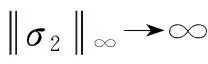
(38)

即σ2∈L2，同时

(39)

(40)

即滑模面σ2是渐近稳定的，同理滑模面σ4也是渐近稳定的.根据滑模面设计过程(8)、(9)和双曲正切函数特性可知，当滑模面σ2和σ4渐近稳定时，有

(41)

即所有状态量也同样是渐近稳定的.

3 仿真结果

绳系系统的面内运动不会激发面外运动，为了分析本文提出的面内摆角控制方法的有效性，本节对分层迭代非线性滑模控制方法和传统控制方法进行比较[7].

仿真初始轨道为圆轨道，半径为7 000 km，推力加速度的横向分量和径向分量如下：

fu=afsin(ωft),fr=afcos(ωft)

其中，af=0.01 m/s2，ωf=π/3 500.系绳长度l=20 m，面内外摆角为θ=10°,φ=1°.期望的状态为系绳绳长lc=20 m，面内摆角θc=-ωft，面外摆角φc=0°.控制参数为c1=c2=0.005,c3=c4=0.000 5,α=β=1,λ=0.1,η=0.01,cs=1.仿真采样时间为100 ms，仿真结果如图4～9所示.

从仿真结果可知，在轨道机动过程中，采用分层迭代非线性滑模控制可使绳系系统稳定.从图4～5可得，采用的分层迭代非线性滑模控制方法对面外摆角控制几乎没有影响.与传统分层滑模控制[12]和反步分层滑模控制[13]的对比如图6～8所示. 从图6 可以看出，本文提出的分层迭代非线性滑模控制及传统分层滑模控制和反步分层滑模控制都可以在20 min左右将面内摆角稳定在期望值.从图7可以看出，分层迭代非线性滑模控制较反步分层滑模控制与传统的分层滑模控制有较小的振荡幅值.反步分层滑模控制在控制初始控制律很大且过零点，传统的分层滑模初始振荡幅值为3.7 N，而分层迭代非线性滑模控制其控制初始振荡幅值很小，仅为1.5 N.反步分层滑模控制由于在每个子系统反步设计过程中引入了子系统期望状态的反步跟踪过程，引入了反步跟踪误差，而绳系系统控制律的权值b1量值较小，反步过程中子系统的误差很容易造成大的控制输出，则反步分层滑模并不适用于系绳张力有较严格约束的绳系系统.同时传统分层滑模控制由于带有符号函数，在稳定后控制律引入高频抖振现象.本文构造的分层迭代非线性滑模控制，采用双曲正切tanh(·)函数代替符号函数后，系统稳定后控制律平滑没有抖振现象.

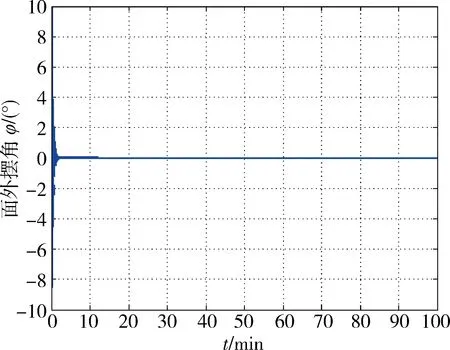
图4 面外摆角Fig.4 Out-of-plane angle φ

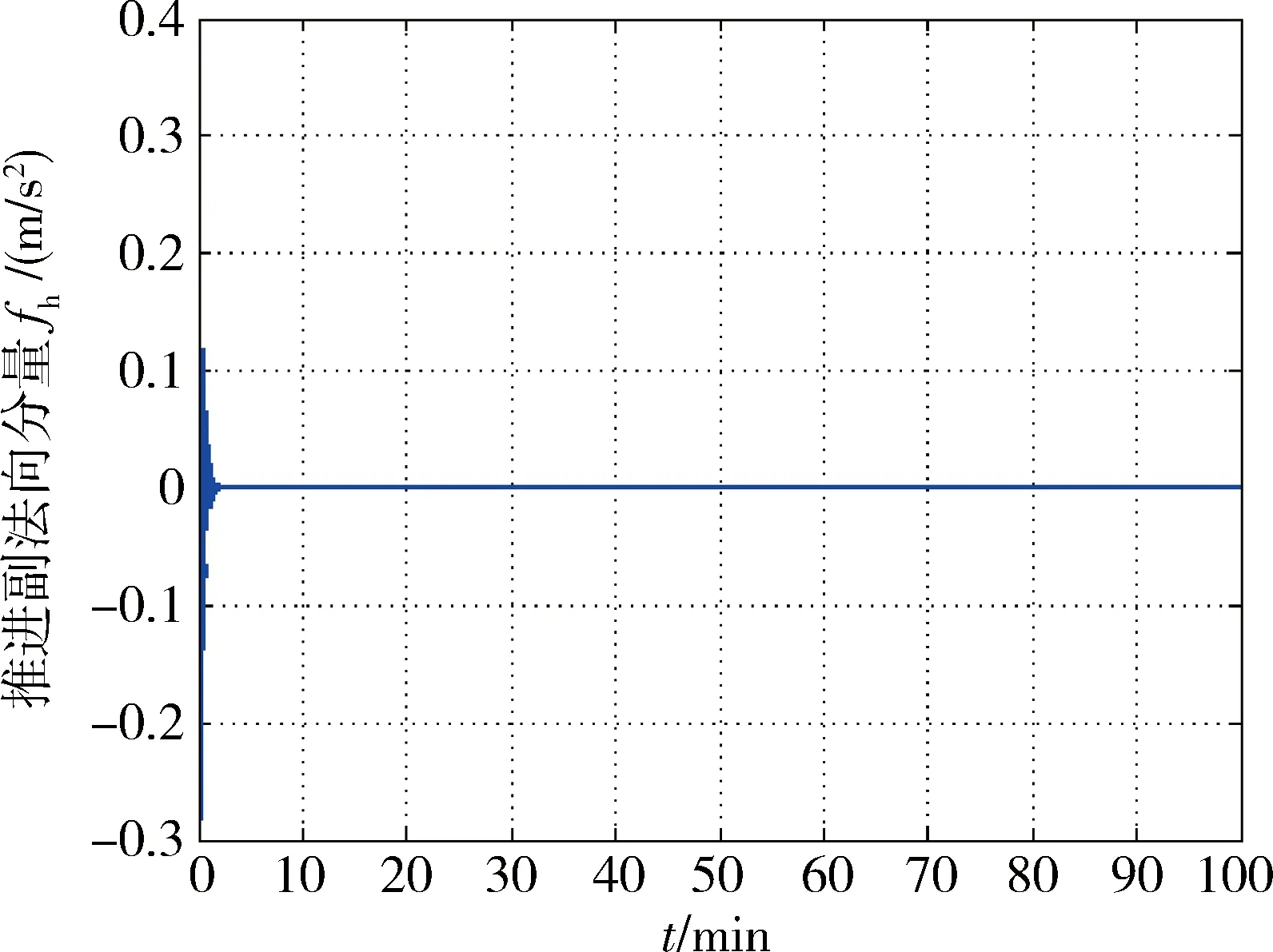
图5 推力的副法向分量Fig.5 Thebinormal component of thrust acceleration fh

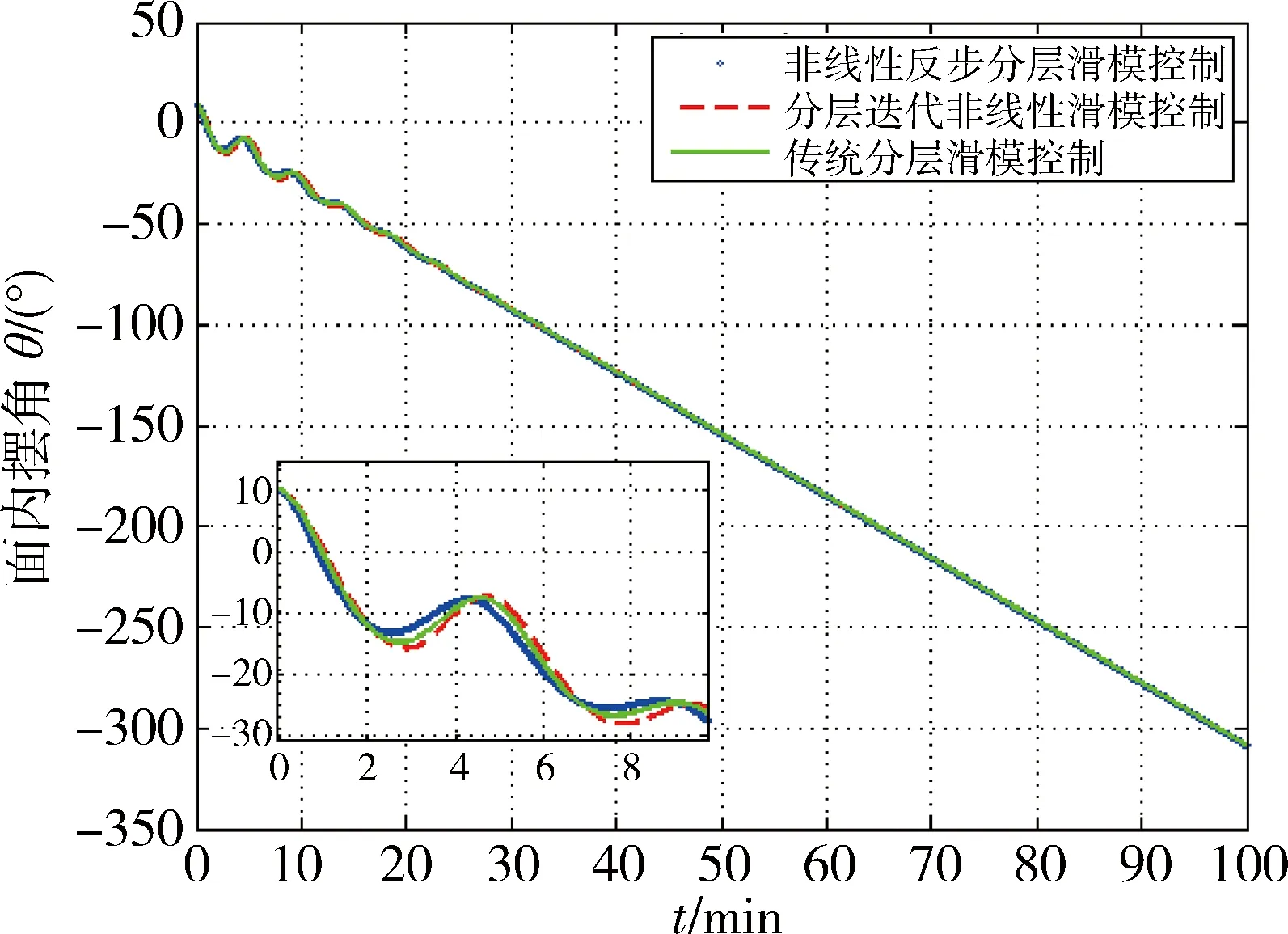
图6 面内摆角Fig.6 In-plane angle θ

从图8系绳绳长可以看出，反步分层滑模控制和传统分层滑模控制在系统稳定后，系绳绳长还存在低幅低频振荡的现象，而相比之下分层迭代非线性滑模控制的系绳绳长稳定后保持在20 m的期望值，控制效果更好.从图9可以看出，分层迭代非线性滑模控制所设计的滑模面都随时间趋于稳定，与证明结果相符.

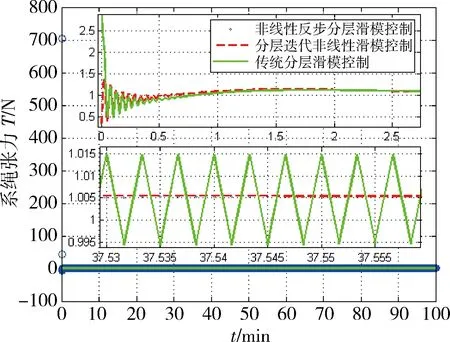
图7 系绳张力Fig.7 Tether tension T

图8 系绳绳长Fig.8 Tether length l

图9 分层迭代非线性滑模控制方法滑模面Fig.9 The sliding surface of hierarchical iteration nonlinear sliding mode control

4 结 论

本文在传统滑模控制方法的基础上，提出了分层迭代非线性滑模控制方法并证明其稳定性.通过数学仿真验证了所提方法的有效性.数学仿真结果表明分层迭代非线性滑模相比于传统分层滑模控制和反步分层滑模控制，控制过程平缓且稳定效果更好.

[1] COSMO M L,LORENZINI E C. Tethers in space handbook[M]. Washington D.C: National Aeronautics and Space Administration, 1997.

[2] 刘海涛, 杨乐平, 张青斌, 等. 地球静止轨道废弃卫星绳系拖曳离轨研究[J]. 中国科学: 技术科学, 2012, 42(7): 780-787. LIU H T, YANG L P, ZHANG Q B, et al. An investigation on tether-tugging de-orbit of defunct geostationary satellites[J]. Scientia Cinica Technology, 2012,42(7): 780-787.

[3] LIU H T, ZHANG Q B, YANG L P, et al.Dynamics of tether-tugging reorbiting with net capture[J]. Science China Technological Sciences,2014, 57(12): 2407-2417.

[4] 刘海涛, 张青斌, 杨乐平,等.绳系拖曳离轨过程中的摆动抑制策略[J]. 国防科技大学学报,2014,36(6): 164-170. LIU H T,ZHANG Q B,YANG LP,et al.Oscillation suppression strategy during tether-tugging reorbiting[J].Journal of National University of Defense Technology, 2014, 36(6): 164-170.

[5] 王道吉.空间绳网展开与离轨拖曳动力学研究[D].长沙：国防科学技术大学, 2012. WANG D J. Dynamics research of expand and tug de-orbit for space rope-net system[D].Changsha: National University of Defense Technology, 2012.

[6] JASPER L, SCHAUB H. Input shaped large thrust maneuver with a tethered debris object[J]. Acta Astronautica, 2014, 96: 128-137.

[7] 孙亮, 赵国伟, 黄海,等.面内轨道转移过程中的绳系系统摆振特性研究[J].航空学报,2012,33(7): 1245-1254. SUN L, ZHAO G W, HUANG H, et al. Analysis oflibrational and vibrational characteristics for tethered systems during orbital transfer in plane[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(7): 1245-1254.

[8] ZHAO G, SUN L, HUANG H. Thrust control of tethered satellite with a short constant tether in orbital maneuvering[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2014: 0954410014521151.

[9] CARTMELL M P, MCKENZIE D J. A review of space tether research[J]. Progress in Aerospace Sciences, 2008, 44(1): 1-21.

[10] LIU H L, HE Y Z, TAN S P, et al.Quasi-continuous high-order sliding mode based controller for tethered satellite with chemical propulsion[C]//2015 IEEE International Conference on Information and Automation. New York: IEEE, 2015: 2197-2202.

[11] 闵颖颖, 刘允刚. Barbalat 引理及其在系统稳定性分析中的应用[J]. 山东大学学报: 工学版, 2007, 37(1): 51-55. MIN Y Y, LIU Y G. Barbalat Lemma and its application in analysis of system stability[J]. Journal of Shandong University(Engineering Science), 2007, 37(1): 51-55.

[12] WANG W, LIU X D, YI J Q. Structure design of two types of sliding-mode controllers for a class of under-actuated mechanical systems[J]. IET Control Theory Application, 2007,1(1):163-712.

[13] 林壮, 段广仁, 宋申民. 水平欠驱动机械臂的反步自适应滑模控制[J]. 机器人, 2009, 31(2): 131-136. LIN Z, DUAN G R, SONG S M.Baekstepping adaptive sliding mode vontrol for horizontal underactuated manipulators[J]. Robot, 2009, 31(2): 131-136.

Librational Controller Design for a Tethered SatelliteSystem during Orbital Maneuvering

XUE Chao1, TAN Shuping1,2, LIU Helong1

(1.BeijingInstituteofControlEngineering,Beijing100090，China; 2.ScienceandTechnologyonSpaceIntelligentControlLaboratory,Beijing100190，China)

A controller is designed to restrain the in-plane libration of a tethered satellite system (TSS). To stabilize the in-plane subsystem of TSS, a hierarchical iterative nonlinear sliding mode control is proposed. The stability of the closed-loop system is also proved. The validity of the proposed algorithm is demonstrated by numerical simulation results. Moreover, the advantages of the algorithm are presented via comparing with the traditional hierarchical sliding mode control.

tethered satellite system; sliding mode control; orbital maneuvering

资助项目(61304037). 收稿日期：2017-01-29

V448

A

1674-1579(2017)02-0021-07

10.3969/j.issn.1674-1579.2017.02.004

薛 超(1993—), 男，硕士研究生，研究方向为航天器控制；谈树萍(1978—)，女，高级工程师，研究方向为航天器姿态控制理论及工程；刘贺龙(1988—)，男，博士研究生，研究方向为空间操作技术.