星载观测平台的视线测量误差分配*

丁文哲，张占月，杨 虹，朱冬骏，陈 峰

(1.装备学院 研究生管理大队，北京 101416； 2.装备学院 航天指挥系，北京 101416)



星载观测平台的视线测量误差分配*

丁文哲1，张占月2，杨 虹1，朱冬骏1，陈 峰1

(1.装备学院 研究生管理大队，北京 101416； 2.装备学院 航天指挥系，北京 101416)

面向光学卫星观测平台的视线测量精度需求，研究了一种基于区间分析理论的误差分配方法.基于先进的卫星、转台、相机结构，建立了惯性系下空间相机与目标间的视线矢量测量模型及测量误差模型.根据区间分析理论，给出了误差灵敏度的评价方法.根据星载观测平台的工作空间，得到了各项误差源在三个轴向上的全域最大灵敏度.以全域最大灵敏度为权重系数，建立了星载观测平台视线测量的误差分配模型，通过遗传算法将13项误差源的可行区间松弛致最大.Monte Carlo仿真验证了该误差分配方法的有效性，该方法也同样适用于机载、车载等观测平台的误差分配研究.

星载观测平台；视线测量误差；区间分析；误差分配

0 引 言

相比于其他探测技术而言，天基光学探测技术由于其自身所具有的独特优势，而逐渐成为目前的研究热点.近年来，对空间态势感知具有革命性意义的“space-based space surveillance(SBSS)”与“space tracking and surveillance system(STSS)”系统也在不断的发展完善自身[1-2].而星载观测平台是搭建双星光学目标监视系统的重要部分，因此分析星载观测平台的视线测量误差，并对星载观测平台进行误差分配具有重要意义.

同国外相比，国内针对天基光学探测技术的研究起步较晚，张萍等[3]首次提出了星载光学观测系统视线测量误差的概念，谢凯、盛卫东等[4-5]在其基础上考虑了更多误差源的影响，进一步研究了星载光学观测系统的视线测量误差.王卫兵等[6]将光电跟踪仪引入了星载光学观测系统，研究了观测系统对空间目标的定轨.但综合国内外来看，目前对于星载观测平台视线测量误差分配方面的研究还比较少.

鉴于此，本文以星载观测平台为研究对象[7]，对观测平台的视线测量误差分配进行了初步探究.针对由卫星本体、载荷平台、光电跟踪仪、空间相机所组成多体观测系统建立星载观测平台的视线测量误差模型，借助区间理论，定义误差灵敏度系数，计算各项误差源在三轴方向的全域灵敏度，将其作为分配权重系数，借助遗传算法将各项误差源的可行区间松弛致最大，实现星载观测平台的视线测量误差分配，最后通过Monte Carlo仿真验证本文分配方法的有效性，为实际中星载观测平台的精度设计提供了一定的参考.

1 模型搭建

1.1 成像过程分析

星载观测平台的视线测量矢量定义为空间目标与星载观测平台上CCD相机间连线在地心惯性坐标系下的单位空间矢量.

星载观测平台在进行成像探测时，通过读取目标在空间相机像素平面上的位置信息，利用坐标变换从而得到目标的相对角度信息，即一般意义上的方位角与高低角.为了更方便直观的分析星载观测平台的视线测量误差，进行误差分配，本文通过构建星载观测平台的视线测量矢量，将目标与星载观测平台间的相对角度信息从传感器坐标系扩展到 惯性空间坐标系.

针对文献[7]中所采用的观测结构，对观测矢量模型进行构建.观测卫星主体由卫星本体、载荷平台组成，通过控制载荷平台上的两轴两框架式光电跟踪仪对目标进行成像跟踪，当跟踪仪活动不能满足对目标的继续跟踪时，则调整卫星姿态，配合跟踪仪使目标重新出现在像面上，以保持继续跟踪.其中载荷平台及跟踪仪结构如图1所示.

图1 载荷平台及跟踪仪Fig.1 Loading platform and tracker

1.2 视线矢量测量模型及测量误差模型

建立星载观测平台视线矢量测量模型，涉及9个坐标系，需要经历16次坐标变换，整个转换过程如图2所示.

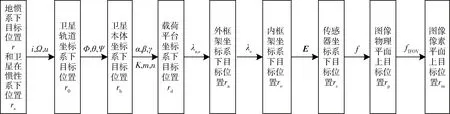
图2 成像过程Fig.2 Imaging process

图2中各变量含义如下：轨道参数(i,Ω,u)分别表示轨道倾角、升交点赤经、纬度俯角；姿态参数(φ,θ,ψ)分别表示滚转角、俯仰角、偏航角；平台参数 (α,β,γ)、(k,m,n)分别表示平台安装角与平台安装位置，框架参数λa、λe、s分别表示平台内、外框架转角及外框架安装高度；E为单位阵；f表示空间相机焦距；fIFOV为瞬时视场角.

首先进行成像变换，整个变换分为两部分：目标从地惯系到传感器坐标系的成像映射及目标从传感器坐标系到像面坐标系的成像映射.

1)地惯系到传感器坐标系的成像映射

rc=Ry(λe)Rx(λa){Rx(α)Ry(β)Rz(γ)
[Rx(φ)Ry(θ)Rz(ψ)BRz(u)Rx(i)
Rz(Ω)(r+Tlo+Tbd)]+Tda}

(1)

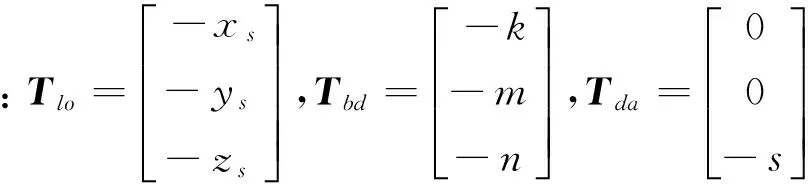
(2)传感器坐标系到像面坐标系的成像映射

(2)

(3)

rm=h(rc)

(4)

式中，[·]表示取整，h(·)表示式(4)的量化函数.

由于k,m,n,s≪|r-rs|，可以忽略星载观测平台安装位置及观测平台上外框架安装高度对单位化的影响.

将式(1)两边同时除以|r-rs|得：

vc=Ry(λe)Rx(λa)Rx(α)Ry(β)Rz(γ)Rx(φ)
Ry(θ)Rx(ψ)BRz(u)Rx(i)Rz(Ω)v

(5)

式中，vc为空间相机与目标在传感器坐标系下的单位连线矢量，v为卫星观测矢量.

式(5)取逆得卫星观测矢量：

v=Ry(λe)Rx(λa)Rx(α)Ry(β)Rz(γ)Rx(φ)
Ry(θ)Rz(ψ)BRz(u)Rx(i)Rz(Ω))-1h-1(rm)

(6)

对式(6)作一阶微分得：

dv=Du,i,ΩdAu,i,Ω+Dφ,θ,ψdAφ,θ,Ω+Dα,β,γdAα,β,γ+
Dλadλa+Dλedλe+DIFOVdrm

(7)

式(7)为星载观测平台的视线测量误差模型，其中dv=[dvx,dvy,dvz]Τ为地惯系中三轴方向的视线测量误差；dAu,i,Ω=[du,di,dΩ]Τ为轨道误差；dAφ,θ,ψ=[dφ,dθ,dψ]Τ为姿态误差；dAα,β,γ=[dα,dβ,dγ]Τ为平台振动误差；dλe、dλa为内、外框架转动误差； drm=[dxm,dym]Τ为像素平面测量误差；Du,i,Ω、Dφ,θ,ψ、Dα,β,γ、Dλa、Dλe、DIFOV是误差传递灵敏度系数矩阵，具体表达式从略.

2 误差灵敏度评价

2.1 误差灵敏度指标

区间分析，是用区间变量代替点变量进行运算的数学分支.它最初是从计算数学的误差理论研究发展起来的.根据区间分析理论，将影响星载观测平台视线测量精度的13项误差源表示为区间向量形式，进行接下来的误差分配.

将各项误差表示为：

dε=[du,di,dΩ,dφ,dθ,dψ,dα
dβ,dγ,dλe,dλa,dxm,dym]Τ

(8)

将式(7)写为区间向量形式：

[dv]=D[dε]

(9)

式中D表示误差映射矩阵.

考虑[dε]中第j项误差[dεj]对视线测量矢量误差在第i轴方向分量[dvi]的作用时，可得式(10)如下：

[dvi,j]=Di,j[dεj]

(10)

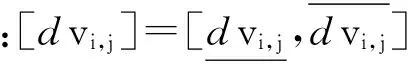
定义由[dεj]到[dvi,j]的区间扩张因子如下：

(11)

当第j项误差[dεj]对第i轴方向视线测量矢量误差[dvi,j]为正影响时，式(11)取正，反之取负.

将灵敏度定义为：

μi,j=ηi,j

(12)

由于卫星在观测过程中工作状态不断发生改变，各项误差源对最终星载观测平台视线测量矢量在三轴方向上的影响也会不断发生改变，定义[dεj]对[dvi,j]的全域最大灵敏度为：

(13)

2.2 全域最大灵敏度计算

根据观测任务，可以给出星载观测平台的工作空间，这里设观测卫星在轨道倾角、升交点赤经分别为81.223 2°、32.006 2°的轨道上运行；载荷平台在卫星上的3个安装角均为20°.观测卫星的可行工作域为：纬度幅角u∈[0，360°]，卫星姿态角φ∈[-180°，180°]，θ∈[-90°，90°]，ψ∈[0，360°]，内、外框架转角λe∈[30°，150°]，λa∈[30°，150°]，目标点成像位置xm∈[0，102 4]，ym∈[0，102 4].

以上述星载观测平台工作域所涉及的8个变量作为约束条件，将13项误差源在3个轴向上的全域最大灵敏度作为目标函数，利用遗传算法工具箱求解这39组约束方程，得13项误差源在3个轴向上的全域最大灵敏度，如表1～3所示.

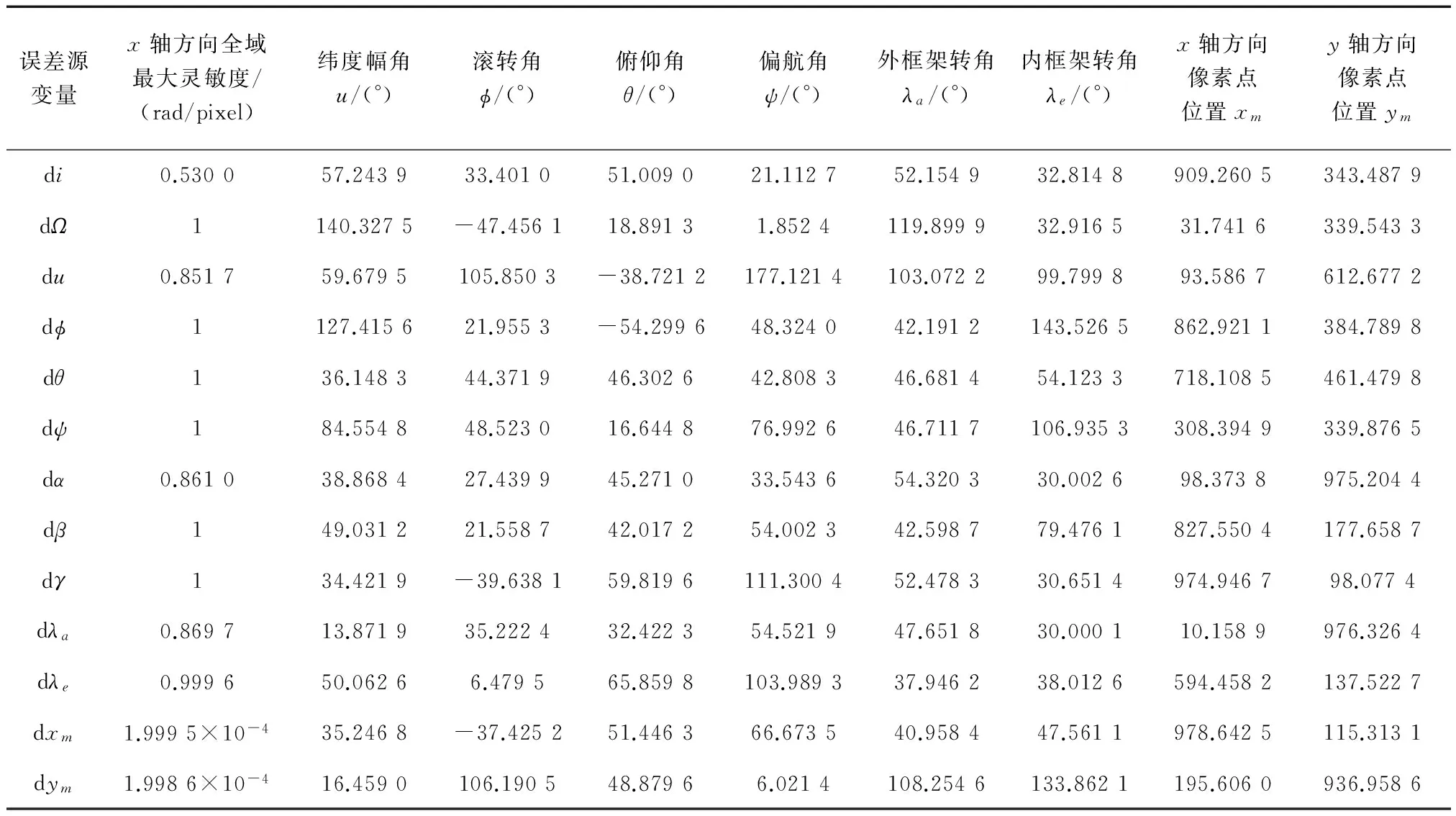
表1 误差源在x轴方向的全域最大灵敏度Tab.1 The global maximum sensitivities of error sources on the x axis

表2 误差源在y轴方向的全域最大灵敏度Tab.2 The global maximum sensitivities of error sources on the y axis

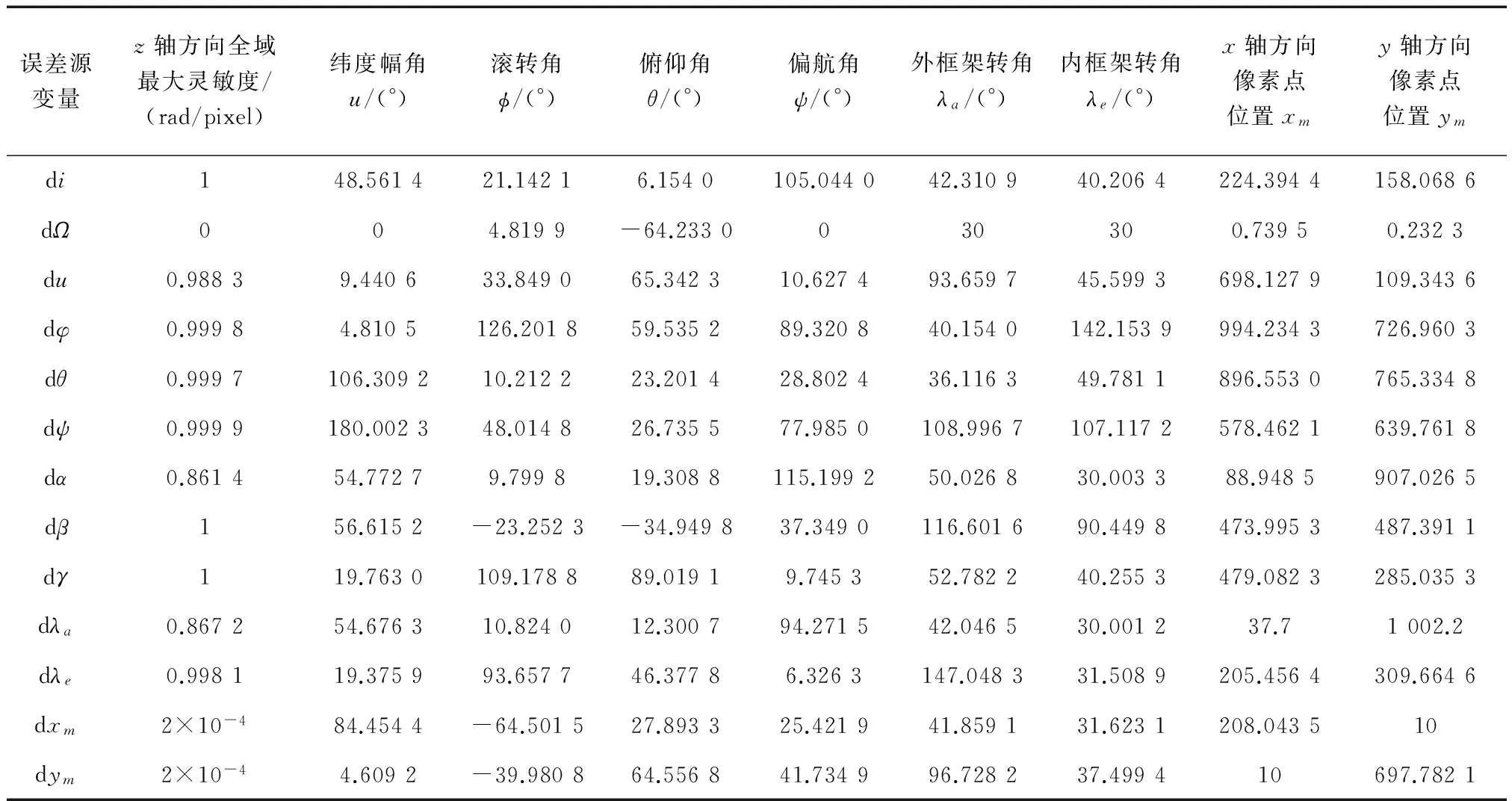
表3 误差源在z轴方向的全域最大灵敏度Tab.3 The global maximum sensitivities of error sources on the z axis

表1～3中各行数据表示当星载观测平台在所取工作状态下观测时，13项误差源在3个轴向上达到最大灵敏度.

通过表1～3，可以分析各项误差源对最终星载观测平台视线测量精度的影响.由于像素点量化误差dxm、dym的全域最大灵敏度具有量纲，不与其它误差源进行比较.

在x轴方向上，误差源dΩ、dφ、dθ、dψ、dβ、dγ、dλe对观测平台视线测量精度的影响最大，du、dα、dλa次之，di最弱.

在y轴方向上，误差源dΩ、dφ、dθ、dψ、dβ、dγ、dλe对观测平台视线测量精度的影响最大，di、dα、dλa次之，du最弱.

在z轴方向上，误差源di、du、dφ、dθ、dψ、dβ、dγ、dλe对观测平台视线测量精度的影响最大，dα、dλa次之，dΩ最弱.

在三轴方向上，像素点量化误差dxm、dym对观测平台视线测量精度的影响基本相同.

3 误差分配

3.1 分配设计

将星载观测平台投入使用之前，必须采用各种标校手段，将各项误差控制在合理范围之内，以保证最终的观测误差.

(1)将13项误差用dε1，dε2，…,dε13表示,并写为区间向量形式：

[dε]=([dε1] [dε2] … [dεk])Τ

(14)

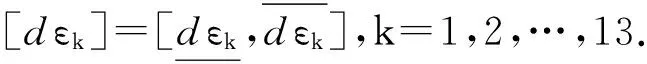
(2)假设各项误差源在可松弛区间内的调整难易均相同，将13项误差松弛至最大的可行区间，构建误差分配的目标函数如下：

(15)

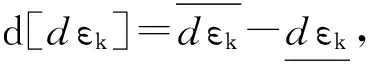
(3)实际中不可能完全消除各项误差，为方便控制各项误差，给各项误差留有一定余量，取13项误差的可行区间如下：

(16)

将星载观测平台在3个轴向上的视线测量精度均控制在300 μrad以内

(17)

(4)结合式(15)～(17)，构建误差分配模型如下：

(18)

适应度函数是由目标函数确定的用于区分群体中个体好坏的标准.利用遗传算法求解式(18)，适应度曲线如图3所示.

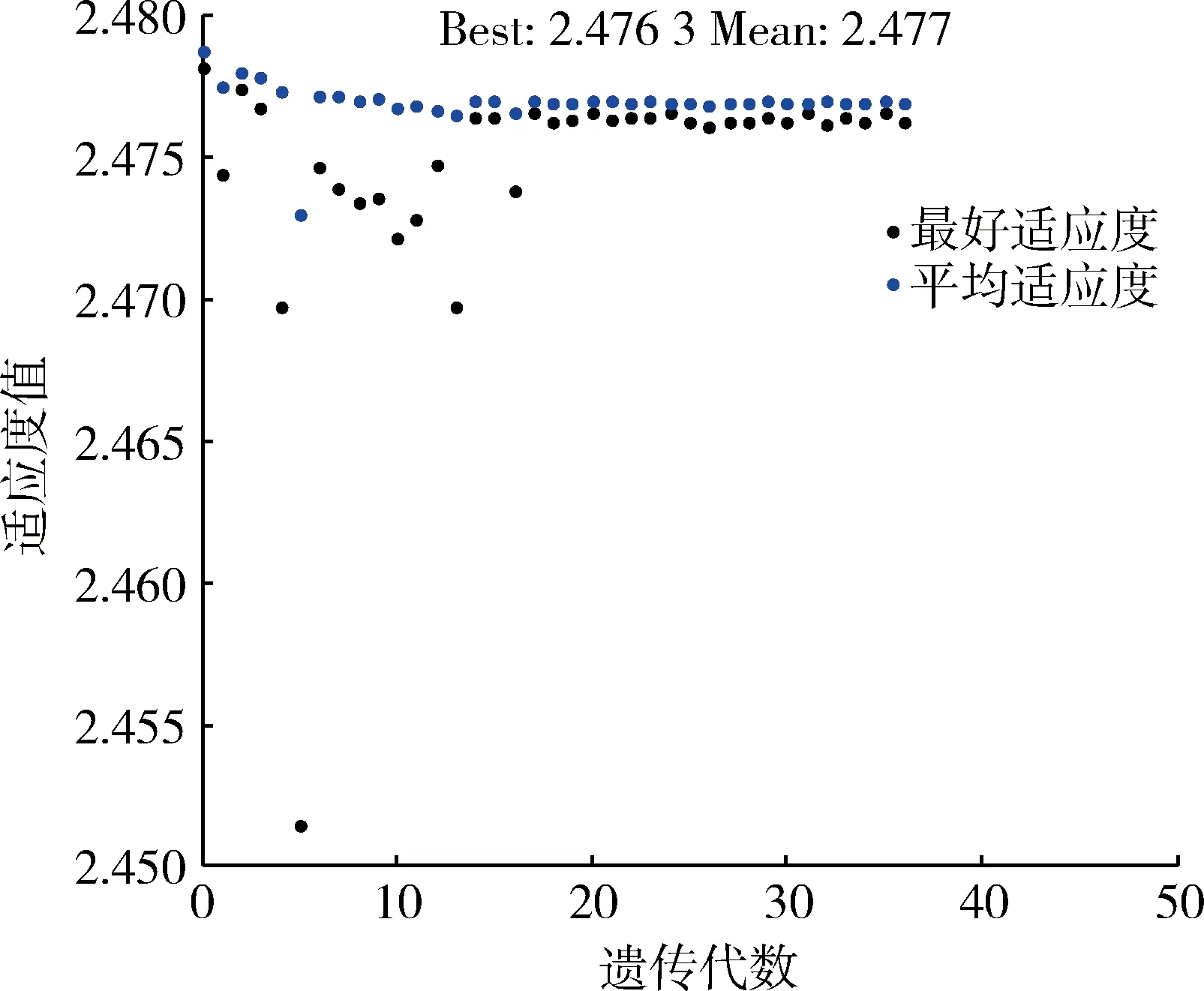
图3 适应度曲线Fig.3 Fitness curve

得到13项误差源的分配区间最优解如表4所示.

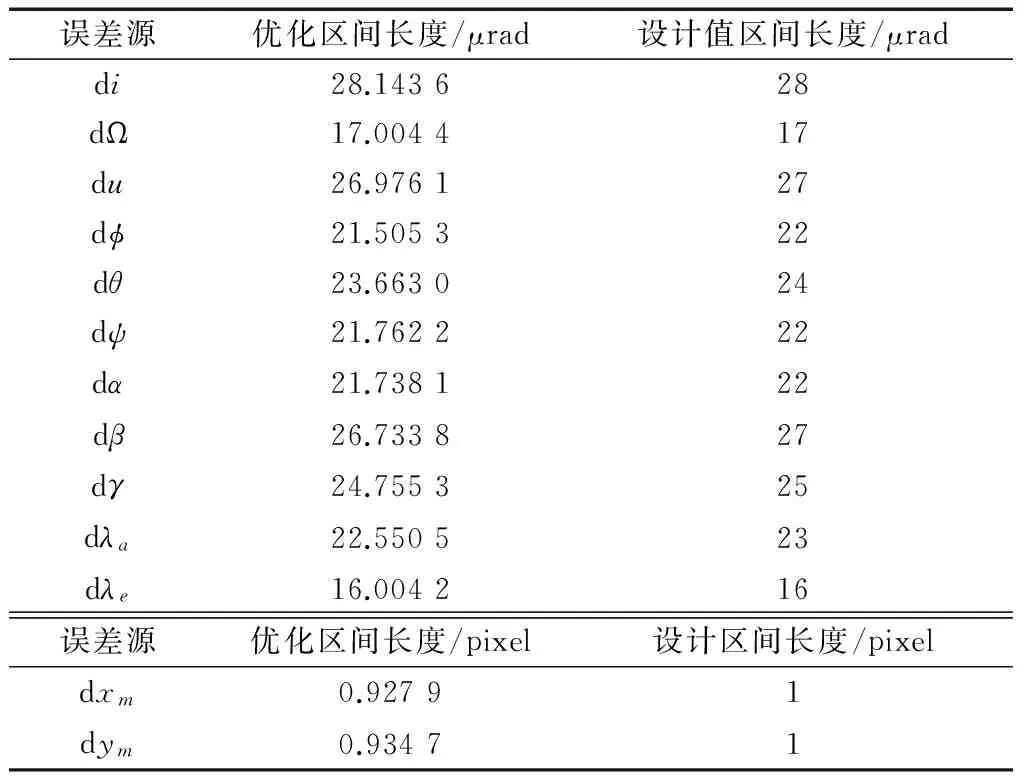
表4 优化结果Tab.4 Optimization results

3.2 Monte Carlo仿真验证

根据3.1节中所得到的误差分配结果，取13项误差在可行空间中的最大值，同时在星载观测平台的工作任务空间中，随机生成15 000个观测状态，仿真得到3个轴向上的星载观测平台视线测量误差，如图4～6所示.

从图4～6中可以看出，星载观测平台最终视线测量误差远小于所要求的300 μrad.仿真统计得到在三轴方向上，星载观测平台视线测量误差小于195 μrad的概率分别为99%、97%、99%，可知按此误差分配方案进行误差设计，可给卫星观测平台提供100 μrad的容错空间，占整个误差限定空间的33.3%，大大提高了系统观测的可靠性.由此可以验证3.1节中所设计误差区间的合理性以及本文误差分配方法的正确性.

图4 x轴误差分布Fig.4 The distribution of errors on the x axis

图5 y轴误差分布Fig.5 The distribution of errors on the y axis

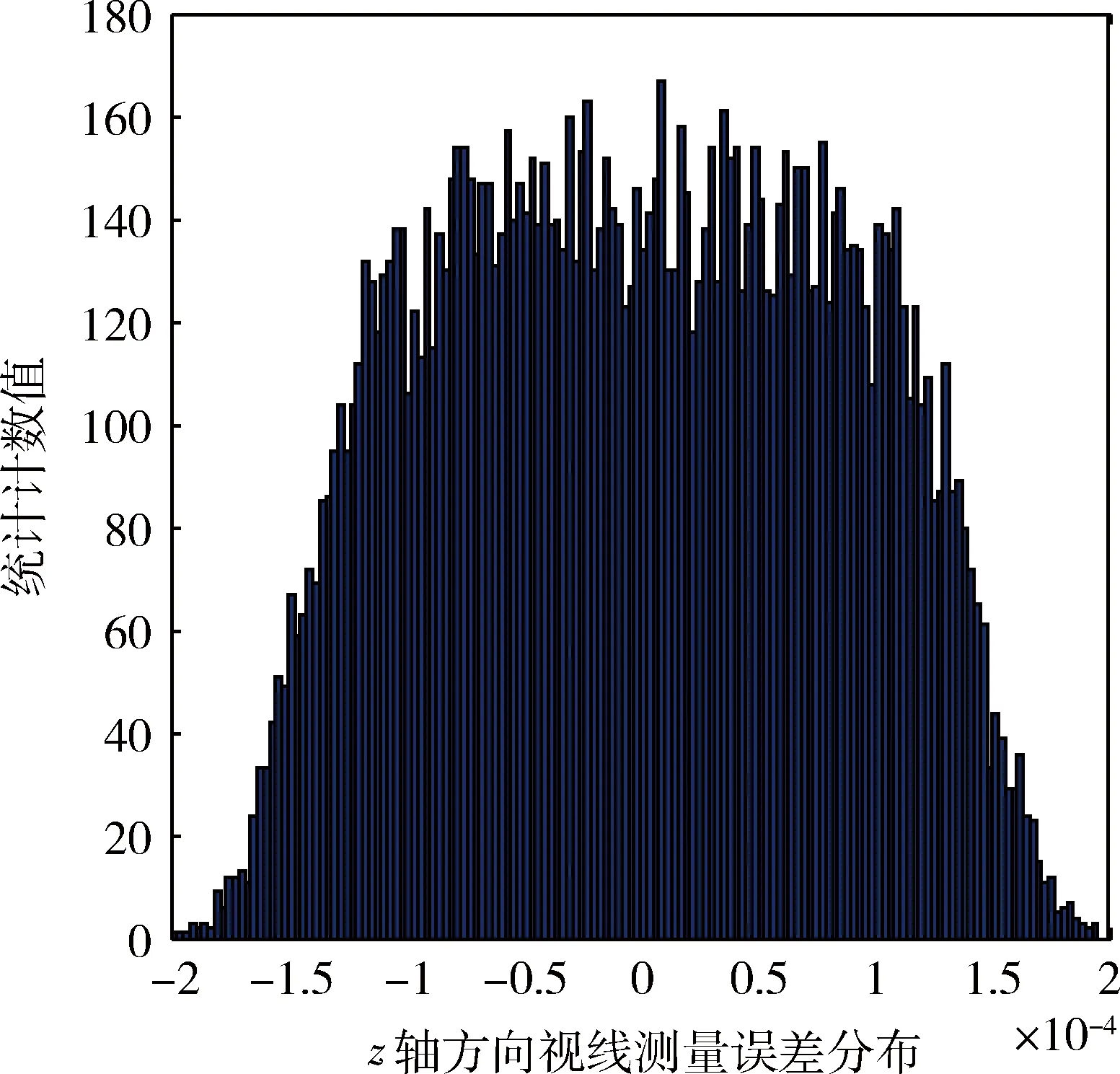
图6 z轴误差分布Fig.6 The distribution of errors on the z axis

4 结束语

面向光学卫星观测平台的视线测量精度需求，研究了一种基于区间分析理论的误差分配方法.首先根据星载观测平台的观测方式构建了观测平台的视线测量模型及测量误差模型;其次通过引入区间分析理论，仿真计算得到了平台观测过程中13项误差源在3个轴向上的全域最大灵敏度；接着以此作为分配权重，建立了星载观测平台视线测量的误差分配模型，利用遗传算法将各项误差源的可行区间松弛致最大；最后通过Monte Carlo仿真试验验证了本文误差分配方法的有效性.接下来可再结合平台设计预算、误差控制成本等因素进一步完善平台设计.

[1] TANG Y,ZHONG W N,LI S. An improved double r-iteration IOD method for GEO UCTs based on SBSS system[J]. Chinese Journal of Space Science, 2014, 34(6): 867-871.

[2] VANDENBERG A C. STSS demo satellites track two-stage interceptor in missile defense test[EB/OL]. http://www.asdnews.com/news, 2010-7-8.

[3] 张萍,易东云,吴翊,等. 空间预警系统的视线测量误差特性研究[J]. 中国空间科学技术,2004,6:51-56. ZHANG P, YI D Y, WU Y, et al. The LOS measurement error modeling of space early warning system[J]. Chinese Space Science and Technology , 2004,6:51-56.

[4] 谢恺,韩裕生,薛模根,等. 低轨红外预警星座无源定位精度分析[J]. 信号处理,2008,3:343-348. XIE K, HAN Y S, XUE M G, et al. Analysis of passive location accuracy in LEO infrared early warning constellation[J]. Signal Processing, 2008,3:343-348.

[5] 盛卫东,徐洋,周一宇,等. 天基光学传感器的视线测量误差分析[J]. 宇航学报,2011,32(1):129-135. SHENG W D，XU Y，ZHOU Y Y, et al. Analysis of LOS measurement error for space-based optical sensor[J]. Journal of Astronautics, 2011,32(1):129-135.

[6] 王卫兵,王挺峰,郭劲. 基于星载光电成像跟踪测距的空间目标定轨[J]. 光学精密工程,2015,23(2):528-539. WANG W B, WANG T F, GUO J. Orbit determination for space target based on opto-electrical imaging, tracking and ranging on satellite[J]. Optics and Precision Engineering, 2015, 23(2): 528-539.

[7] 杨虹, 张占月, 丁文哲, 等. 双星光学观测体系的目标定位误差分析[J]. 中国光学, 2016, 9(4): 452-462. YANG H, ZHANG Z Y, DING W Z, et al. Position error analysis of double satellites optical observation system. Chinese Optics, 2016, 9(4): 452-462.

[8] 田文杰． 精密卧式加工中心几何精度设计及误差补偿方法研究[D]． 天津: 天津大学机械工程学院，2014. TIAN W J. Investigation into accuracy design and error compensation of high-precision horizontal machining centers[D]．Tianjin: School of Mechanical Engineering，Tianjin University，2014．

Error Distribution of Line-of-Sight Measurement on theSatellite Borne Observation Platform

DING Wenzhe1， ZHANG Zhanyue2， YANG Hong1， ZHU Dongjun1， CHEN Feng1

(1.DepartmentofGraduateManagement，EquipmentAcademy，Beijing101416，China；2.DepartmentofSpaceCommand，EquipmentAcademy，Beijing101416，China)

Focusing on the requirement of Los measurement accuracy for the optical satellite observation platform, an error distribution method is studied based on interval analysis theory. Based on the structure of advanced satellite, turntable and camera, the line-of-sight vector measurement model and measurement error model between the space camera and the target are established. According to the interval analysis theory, the evaluation method of the error sensitivity is presented. According to the working space of satellite observation platform, the global maximum sensitivity of the error source in three-axis is get. Setting the global maximum sensitivity as weight coefficient, the error distribution model of the line-of-sight measurement of satellite borne observation platform is established. The maximum of 13 error sources is reached by genetic algorithm. Monte Carlo simulation shows that the method is effective, and the method is also applicable to the error distribution of the airborne, vehicle and other observation platforms.

satellite borne observation platform； line-of-sight measurement error； interval analysis； error distribution

收稿日期：2016-12-18

TH122

A

1674-1579(2017)02-0060-07

10.3969/j.issn.1674-1579.2017.02.010

丁文哲(1992—)，男，硕士生，研究方向为航天任务分析与设计；张占越(1974—)，男，教授，研究方向为航天作战指挥；杨 虹(1991—)，女，硕士研究生，研究方向为航天任务分析与设计；朱冬骏(1991—)，男，硕士研究生，研究方向为航天任务分析与设计.