基于J2-积分与六棱柱壳裂纹应力强度因子

刘明岳， 谢禹钧, 李 岩， 李世杰， 魏 巍

(1.辽宁石油化工大学 机械工程学院，辽宁 抚顺113001；2.中国石油天然气股份有限公司 抚顺石化分公司，辽宁 抚顺113001；3.中石化第五建设有限公司，广东 茂名525000)

基于J2-积分与六棱柱壳裂纹应力强度因子

刘明岳1， 谢禹钧1, 李 岩1， 李世杰2， 魏 巍3

(1.辽宁石油化工大学 机械工程学院，辽宁 抚顺113001；2.中国石油天然气股份有限公司 抚顺石化分公司，辽宁 抚顺113001；3.中石化第五建设有限公司，广东 茂名525000)

应力强度因子作为一个重要的断裂参量，在工程结构件断裂分析过程中起到至关重要的作用。本文基于J2-积分和材料力学中的弯曲理论，对六棱柱壳横向裂纹和加强筋六棱柱壳横向裂纹的应力强度因子进行了分析求解。给出了利用J2-积分求解复杂结构应力强度因子的一个方法。

应力强度因子；J2-积分； 六棱柱壳； 裂纹

多边棱柱壳是常见的工程结构件，其中具有环向裂纹的六棱柱壳属于典型的复杂三维裂纹结构。在断裂分析中，裂纹应力强度因子是裂尖奇异应力场应力集中程度的度量[1]，是工程结构件断裂分析的重要参量。然而，运用经典解法求复杂三维结构裂纹的应力强度因子十分困难。对于复杂的三维结构，目前的应力强度因子手册给出的公式基本上是用数值法拟合而成的。但这样的公式都是有一定使用条件限制，当使用条件发生变化时就需要做新的数值分析[1]。

本文利用J2-积分和材料力学中的弯曲理论[1-2]，得到了六棱柱壳横向裂纹应力强度因子的封闭解，给出了一种利用J2-积分求解棱柱壳结构横向裂纹应力强度因子的求解方法。

1 守恒积分

对于三维结构，由守恒律给出的Jj-积分,即[1-9]：

(1)

式中，w是应变能密度;Ti是作用于Ω外侧的面力，nj是Ω的外法线矢量;ui,j为积分路径上各点的位移矢量。对于不含孔洞的闭合曲面Ω，(1)式的积分为0。本文将利用上式在具体裂纹问题中的物理意义[3]，构

建求解应力强度因子的方程。

带有横向裂纹的六棱柱壳如图1所示。x2轴与六棱柱壳的轴线方向一致，即垂直于裂纹面,(1)式中的J2-积分为[4]：

(2)

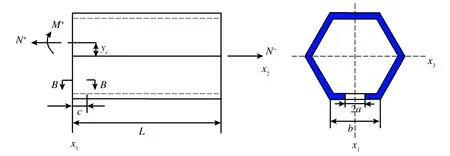
图1 拉伸载荷作用下的六棱柱壳横向裂纹管

Fig.1 Six prismatic shell tube with transverse crack under tension

如图1所示，若Ω取为裂纹面，(2)式的物理意义是裂纹面Ω沿x2方向单位移动所产生的能量释放率。当裂纹面为自由面时，对于裂尖K-控制区的裂纹Ωbb′，由积分守恒和裂纹尖端应力、位移公式可得[5]：

(3)

2 拉伸载荷作用下的六棱柱壳横向裂纹

拉伸载荷作用下六棱柱壳横向裂纹管如图1所示，六棱柱壳边长为b、厚度为t、管长为L、裂纹长度为2a。N是轴向力，yc是裂纹面中性轴位置。符号‘+’为裂纹截面，‘-’为远场非裂纹截面[6]。

2.1 基于J2-积分的裂纹面移动能量释放率

裂纹局部放大示意图如图2所示，在裂纹面Ωaa′b′b内，存在两个相同的奇异场应力，由(2)、(3)式可以得到：

(4)

(4)式的物理意义是，裂纹面Ωaa′b′b沿x2轴单位移动的能量释放率。

2.2 基于弯曲理论的能量释放率

如图3所示，若将裂纹视为由椭圆孔模型由c→0退化而成[8]，于是变截面梁的应变能为：

(5)

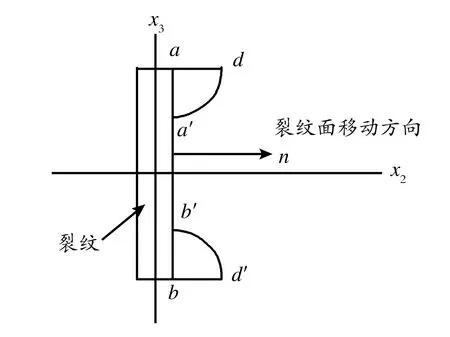
图2 裂纹周边局部放大图

Fig.2 Local wall of pipe around crack

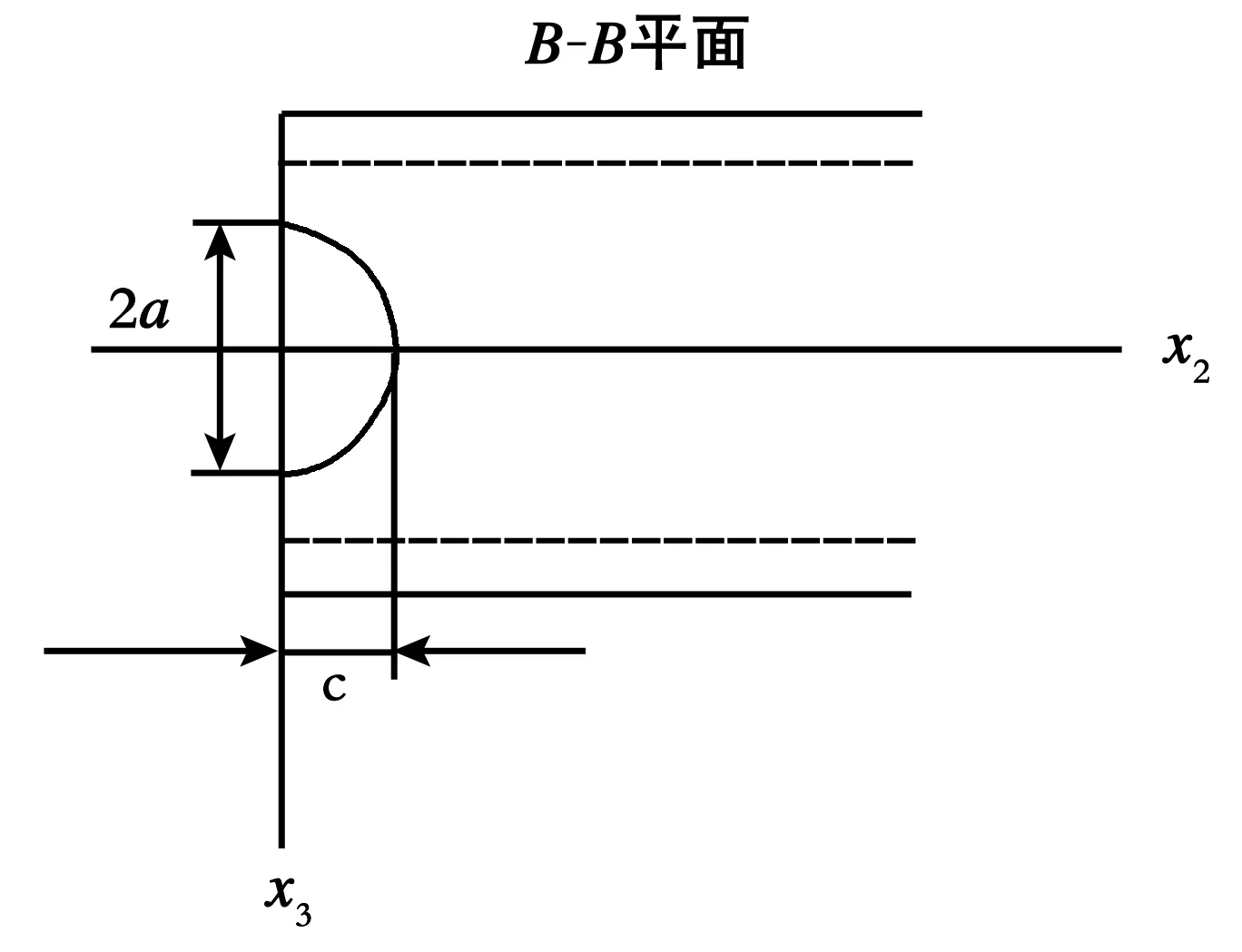
图3 当c→0时裂纹管椭圆孔模型

Fig.3 An elliptical hole model for cracked tubes

(6)

2.3 应力强度因子

式(4)与式(6)的物理意义相同[11]，得式(7)：

(7)

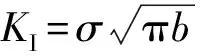
(8)

3 拉伸载荷作用下的加强筋六棱柱壳横向裂纹

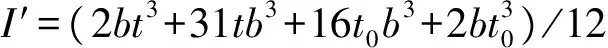
(9)

(10)

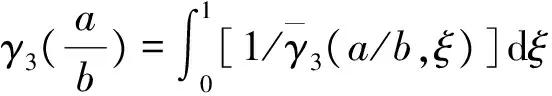
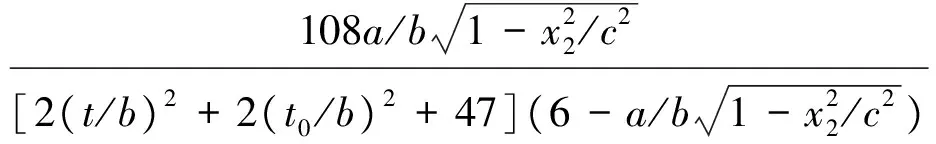
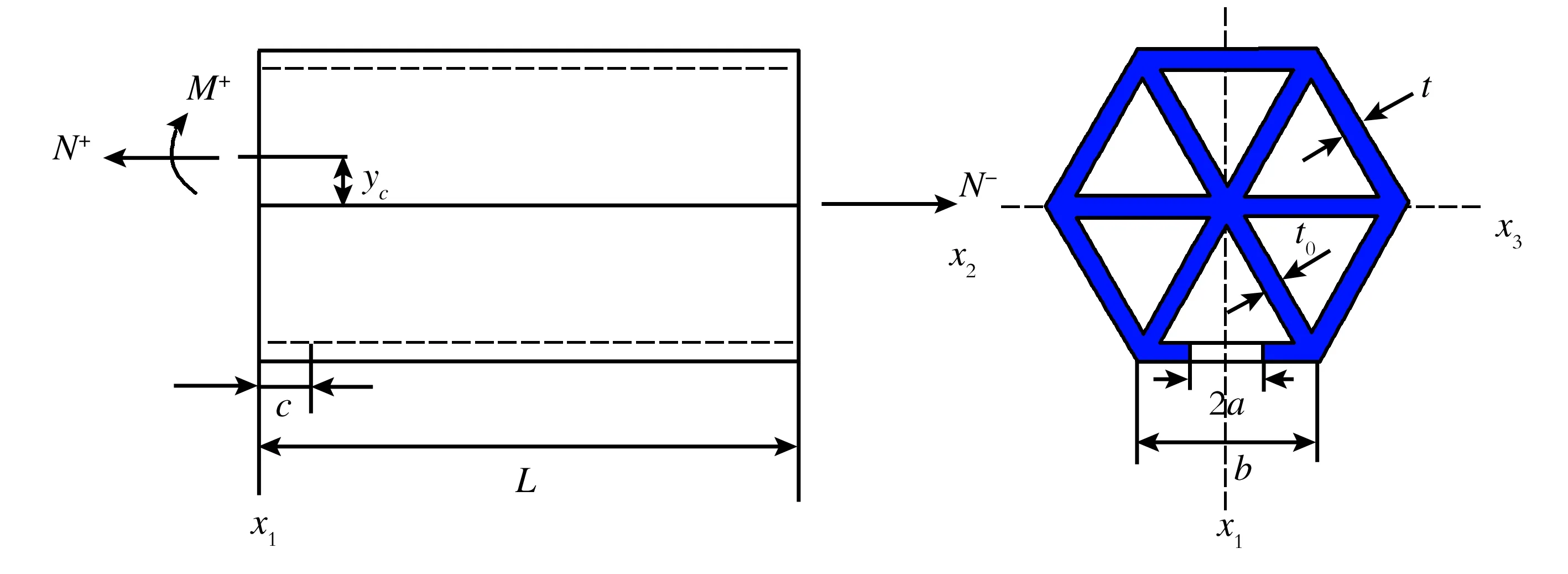
图4 拉伸载荷作用下的加强筋六棱柱壳横向裂纹管

4 算例与结果比较

数值计算采用ABAQUS 6.14有限元分析软件，结构弹性模量E=206 GPa，泊松比μ=0.3，单元类型为八结点线性六面体单元(C3D8)[13]。六棱柱壳和加强筋六棱柱壳边长为b=200 mm，壁厚和筋板厚度为t=t0=1 mm。模型及网格图见图5、图6[14]。两种方法计算得到的正则化应力强度因子结果见图7和图8。

图5 六棱柱壳有限元模型及网格

Fig.5 The finite element model and meshesof six prismatic shell tube

图6 加强筋六棱柱壳有限元模拟及网格

Fig.6 The finite element model and meshes of reinforcement

of six prismatic shell tube

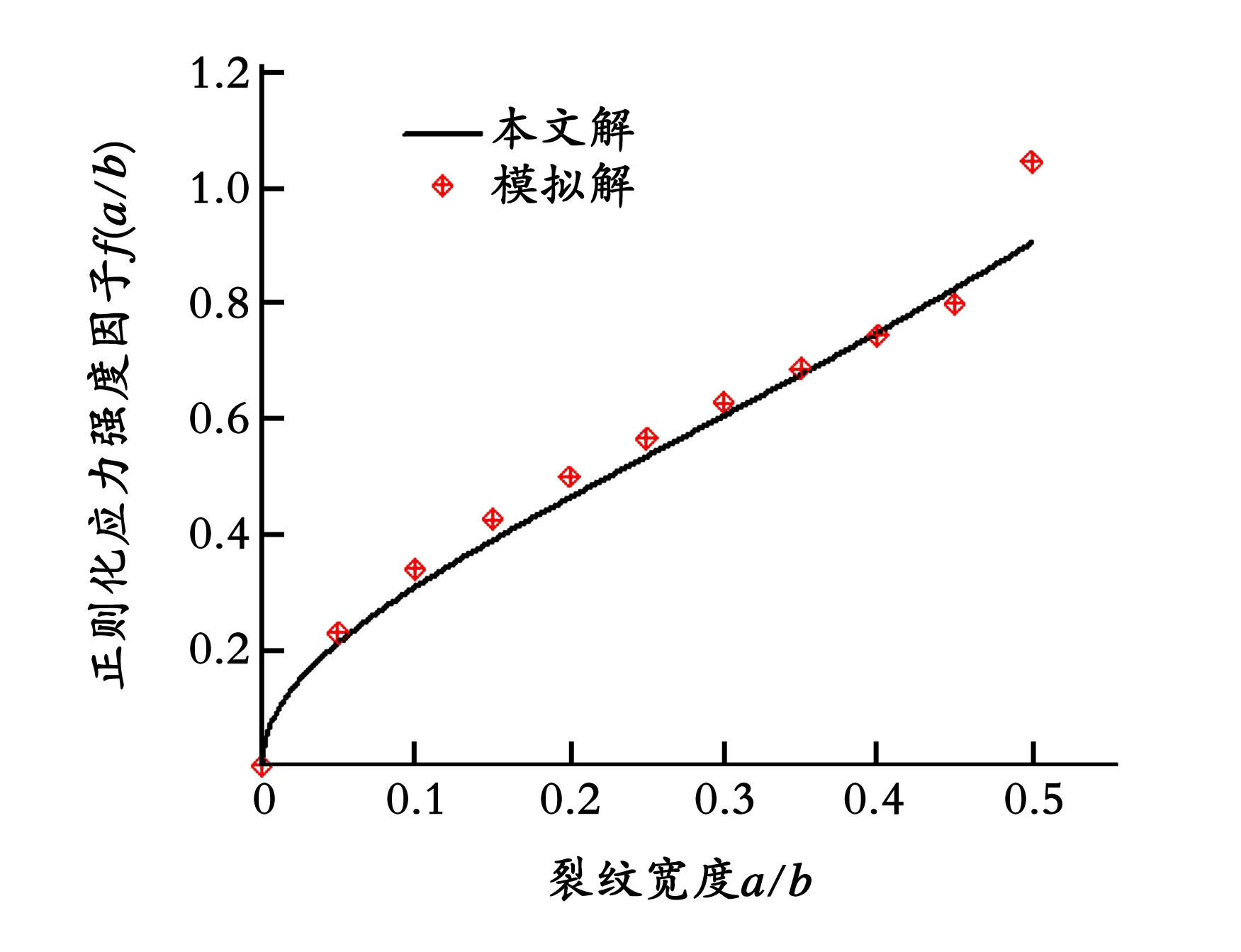
图7 六棱柱壳横向裂纹本文解与有限元解的对比

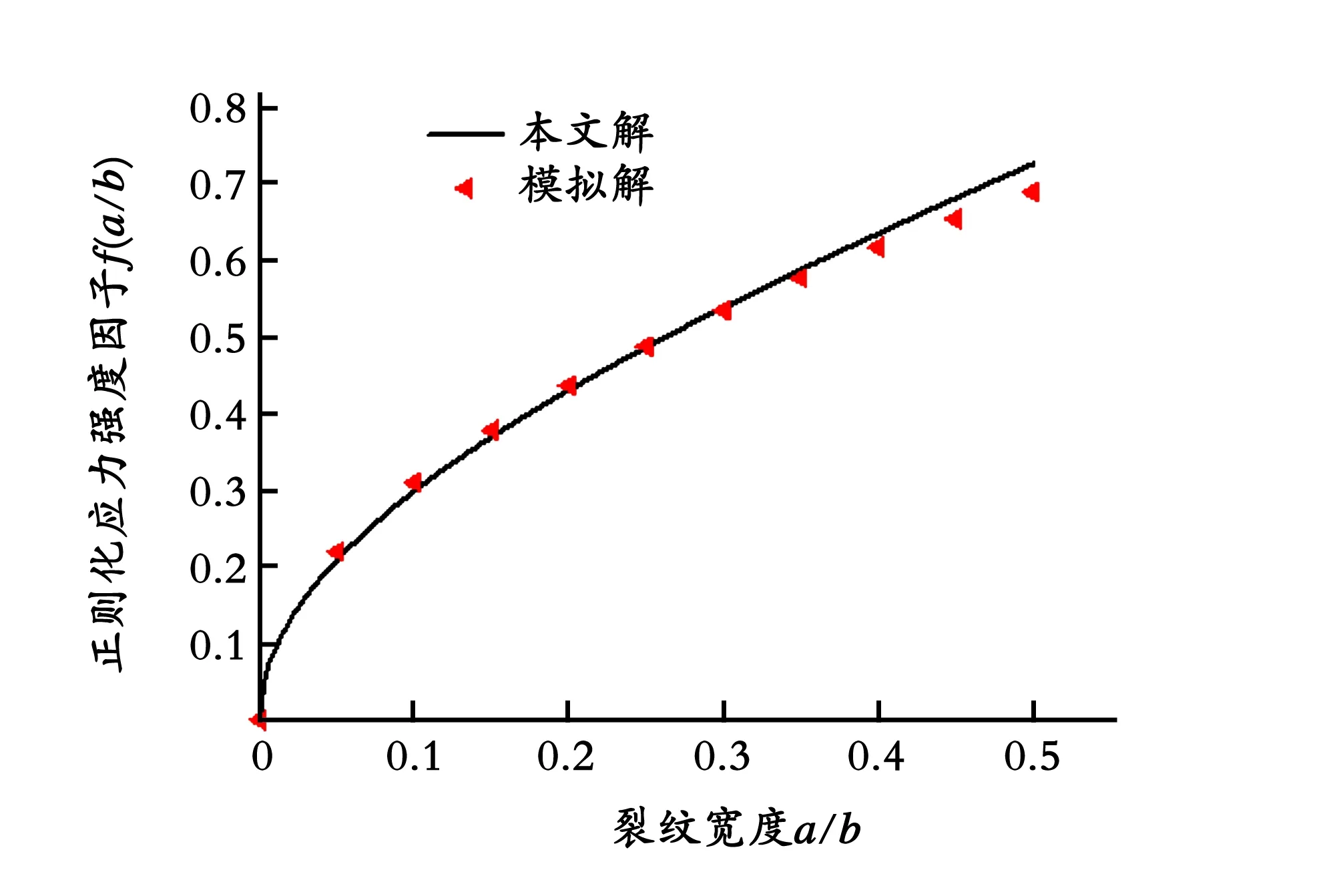
图8 加强筋六棱柱壳横向裂纹本文解与有限元解的对

当t=t0时,随着裂纹长度增加，两者正则化应力强度因子f(a/b)和应力强度因子KI也随之增加，但六棱柱壳横向裂纹的应力强度因子KI1要大于加强筋六棱柱壳横向裂纹的应力强度因子KI2，引入无量纲参数g=KI1/KI2，可以得出g>1[15]。由图7、图8的数值模拟分析结果，表明该方法具有足够的精度。

5 结论

本文基于J2-积分和材料力学中的弯曲理论，对六棱柱壳横向裂纹和加强筋六棱柱壳横向裂纹的应力强度因子进行了分析求解。给出了利用J2-积分求解复杂结构应力强度因子的一个方法。同时，以六棱柱壳为例，给出了带有加强筋和不带加强筋的薄壁裂纹管的应力强度因子的对比，证明了加强筋可以有效降低薄壁裂纹管的应力强度因子。

[1] 程靳，赵树山．断裂力学[M].北京:科学出版社，2006．

[2] 刘鸿文．材料力学[M].北京：高等教育出版社，2011.

[3] Xie Y J,Xu H,Li P N.Crack mouth widening energy-release rate and its application [J]. Theoretical and Applied Fracture Mechanics, 1998,29(3):195-203．

[4] Xie Y J．A theory on cracked pipe[J]. International Journal of Pressure Vessels and Piping, 1998,1(75):865-869．

[5] 徐芝纶．弹性力学[M].北京：高等教育出版社，2013.

[6] Xie Y J,Wang X H.Stress intensity factors for cracked triangular cross section thin-walled tubes [J].Fatigue & Fracture of Engineering Materials & Structures, 2004,27(12):1109-1117.

[7] Xie Y J，Li P N，Xu H．On KIestimates of cracked pipes using an elliptical hole model and elementary beam strength theory of cracked beams [J]．Engineering Fracture Mechanics，1998,59(3):399-402．

[8] Xie Y J,Wang X H.Application of G*-integral on cracked structural beams [J]. Journal of Constructional Steel Research，2004,60(9):1271-1290.

[9] Xie Y J,Wang X H,Lin Y C.Stress intensity factors for cracked rectangular thin-walled tubes [J]. Engineering Fracture Mechanics,2004,71:1501-1513.

[10] 张芳瑶, 陈 松, 蔡永梅, 等. 异型管扭曲环向周期裂纹应力强度因子[J]. 石油化工高等学校学报, 2014, 27(6): 93-96. Zhang Fangyao,Chen Song, Cai Yongmei,et al.Stress intensity factor for special-shaped pipes with periodic cracks[J].Journal of Petrochemical Universities, 2014, 27(6): 93-96.

[11] 谢禹钧．方形截面管横向裂纹的应力强度因子KⅠ[J]．工程力学，2004，21(6)：183-186． Xie Yujun.Stress intensity factors KIfor cracked box beams[J].Engineering Mechanics,2004,21(6):183-186.

[12] 谢禹钧,王晓华,王伟,等. 拉伸环向周期裂纹管的应力强度因子[J]. 工程力学, 2006,23(6):173-176. Xie Yujun,Wang Xiaohua,Wang Wei,et al. Stress intensity factors for circumferential periodic cracked pipes under tension[J].Engineering Mechanics,2006,23(6):173-176.

[13] 庄茁，由小川，廖剑辉，等. 基于ABAQUS的有限元分析和应用[M]. 北京：清华大学出版社，2009.

[14] 胡于进，王璋奇. 有限元分析及应用[M]. 北京：清华大学出版社，2009.

[15] 闫兴清.加强筋止裂性能研究及管件极限载荷计算[D].大连:大连理工大学, 2007.

(编辑 王亚新)

The Stress Intensity Factor of Six Prismatic CrackedShell Based onJ2-Integral

Liu Mingyue1, Xie Yujun1, Li Yan1, Li Shijie2, Wei Wei3

(1.SchoolofMechanicalEngineering,LiaoningShihuaUniversity,FushunLiaoning113001,China;2.PetroChinaFushunPetrochemicalCompany,FushunLiaoning113001,China;3.SINOPECFifthConstructionCompanyLimited,MaomingGuangdong525000,China)

As one of the important fracture parameters, stress intensity factor plays an important role in the fracture analysis of engineering structures.Based on the concept ofJ2-integral and the elementary theory of strength of materials,the stress intensity factors of the transverse crack of the six prismatic shell and the six prismatic shell with reinforcing rib are analyzed and solved. A method for solving the stress intensity factor of complex structure by usingJ2-integral method is presented.

Swess intensity facter;J2-integral; Six prismatic shell; Crack

2016-09-06

2016-11-12

国家自然科学基金项目(50771052, 50971068, 11272141)。

刘明岳(1989-)，女，硕士研究生，从事断裂力学和结构安全研究；E-mail：972464321@qq.com。

谢禹钧(1960-)，男，博士，教授，从事断裂力学、 结构完整性及失效风险等研究；E-mail:yjxie@lnpu.edu.cn。

1006-396X(2017)02-0086-05

投稿网址：http://journal.lnpu.edu.cn

TE905; O346.1

A

10.3969/j.issn.1006-396X.2017.02.016