干气密封摩擦副启停阶段摩擦特性的仿真研究
丁雪兴, 王文鼎, 金海俊, 赵海红
(兰州理工大学 石油化工学院,甘肃 兰州 730050)
干气密封摩擦副启停阶段摩擦特性的仿真研究
丁雪兴, 王文鼎, 金海俊, 赵海红
(兰州理工大学 石油化工学院,甘肃 兰州 730050)
针对干气密封非稳态下摩擦特性对密封性能的影响进行研究,考虑动、静环材料属性,微凸体之间的相互作用以及摩擦热流耦合,建立了三维粗糙实体与理想光滑刚体滑动摩擦热力耦合模型。运用ANSYS软件数值模拟了摩擦热以及应力变化规律。研究发现,粗糙表面最高接触温度随滑动时间增加呈逐步上升趋势,并且温升呈现了一定的波动性;粗糙表面的VonMises等效应力分布极其不均匀呈非线性变化;同时,还发现最大x方向应力分量σxx并未出现在最高接触微凸体上;在沿三维粗糙实体厚度方向存在一拉应力区,随着滑动时间的持续,拉应力区有一定程度扩大。从而说明两端面间的温升和波动性以热传导为主要影响因素,应力的变化是由于微凸体发生了弹塑性变形。研究成果为今后干气密封启停阶段特性研究以及参数优化奠定了基础。
干气密封; 微凸体; 滑动摩擦; 弹塑性变形; 温升; 应力
随着石油化工设备以及旋转机械不断走向极端工况(高温、高速、大振动),干气密封因自身的优势而被广泛应用。据发达国家如英、美、德等国的统计,在石油化学工业中,离心泵占全部机泵设备的85%以上,而离心泵维修工作量70%左右是处理密封失效。但是,在工程应用过程中,设备难免会发生振动以及多次停车与启动,将会对干气密封的稳定运行造成极大的伤害。干气密封启动过程中由干摩擦向气膜润滑转变,在转变过程中端面将会接触摩擦以及升温损伤动环槽面而失效。因此,干气密封启停阶段摩擦磨损的研究对其端面性能尤为重要。
近几十年来,国内外专家学者对其密封微观接触特性进行了广泛而深入的研究,并取得了不少成果。J. A. Archard[1]提出了分析多个微凸体的接触的统计模型,对密封环摩擦表面的接触摩擦性能进行了研究。J. A. Greenwood等[2-3]基于赫兹接触力学和粗糙表面的统计分析提出了G-W弹性接触模型,他们的研究指出真实接触面积、接触微凸体数和载荷均与表面轮廓高度的概率密度函数相关。A.Majumdar等[4]首先基于W-M分形函数建立了新的接触模型,即M-B弹塑性接触分形模型。
M-B模型由于包含了能够表征表面全部特征信息的分形参数,因此M-B模型更为先进,与传统的G-W模型相比,M-B模型能够定量的描述弹性接触面积、塑性接触面积与分形维数的关系。孙见君、顾伯勤和魏龙等[5-7]参照M-B分形接触模型,建立了接触式密封摩擦副端面分形模型,研究了端面形貌变化与机械密封泄漏率之间的关系。
近几年来,利用以上专家学者所提出的摩擦端面模型,使得研究转向摩擦界面温度的变化,国内外学者对此进行了大量的研究。朱维兵等[8]用ANSYS软件计算了机械密封环热变形和热应力。D. Pascovici和I. Etsion等[9-10]推导了机械密封界面处在全流体润滑状态下的温度分布计算表达式。朱孝平等[11]对双端面机械密封处在混合摩擦状态下的传热特点进行了分析,构建了密封界面温度分布的计算模型。周剑锋等[12]研究了机械密封端面摩擦热在整个传热系统(由静环、动环、端面液膜和密封介质组成)中的传递规律。高杰等[13]通过考虑热量在动、静环摩擦界面的分配,以及根据明确定义的热传导角,建立了机械密封摩擦界面在混合润滑状态与全流体润滑状况下的温度计算模型。
综上所述,国内外大量的专家学者主要是从宏观上对密封环温度进行揭示,经过对其端面摩擦磨损的研究,得出M-B及G-W等模型,这些模型被广泛应用。但是,目前研究尚未从微观的角度对温度在摩擦界面的产生及分布进行机理揭示。且大多研究都简化了微凸体的模型,忽略微凸体相互影响,未能考虑多场耦合。基于此建立了微观三维粗糙实体滑动摩擦热力耦合模型,考虑材料的弹塑性变形,微凸体之间的相互作用以及摩擦热流耦合等,并运用大型通用有限元软件ANSYS数值模拟和分析了微观三维粗糙实体滑动摩擦模型的摩擦热及应力分布。
1 模型的建立
1.1 数学模型
微尺度下,干气密封摩擦副端面都是粗糙不平的,摩擦副端面都是由高低不平的微凸体构成。客观准确地表征粗糙表面是研究干气密封启停阶段端面摩擦特性的重要条件。鉴于粗糙表面大多都具有分形特征,其表面轮廓曲线具有统计自彷射分形特征,其分形特征与尺度无关,其分形参数可以很好的描述粗糙表面的形貌信息[14]。并且已有研究表明,接触式密封摩擦端面具有分形行为,因此摩擦副端面可以用处处连续但处处不可导的W-M[15]函数表征和模拟,其表达式为:
(1)
式中,D为表面分形维数;G为特征尺度系数;γ为大于1的常数,通常取1.5;n为空间频率序数;M为曲面褶皱重叠数;φm,n为随机相位,取值范围是[0,2π];Ls为截止长度,近似取材料的原子间距;L为取样长度;最低空间频率序数nl=0;最高空间频率序数nmax=int[lg(L/Ls)/lgγ]。依据电镜测得静环[16]M106K(浸锑石墨)的特征参数如表1所示。

表1 静环特征参数
根据表1中的静环特征参数代入公式(1)中,利用Mathematica软件编程获得静环局部三维粗糙实体如图1所示。
图1所测得的粗糙实体大小为6 μm×6 μm,微凸体呈Gauss分布。

图1 三维粗糙实体模型
Fig.1 3D rough solid model
1.2 几何模型
将干气密封启停阶段的接触摩擦温升过程看作是一个具有三维分形特征的粗糙实体与一个理想光滑刚体接触摩擦来分析。将干气密封的静环看作是三维粗糙实体,动环看作是理想光滑刚体(由于动环的硬度、加工方式及表面粗糙度均优于静环,故假设动环为理想光滑刚体)。但是,由于微观粗糙表面形貌比较复杂且具有很强的随机性,尺度都处在微纳级别,因此常用的三维软件很难建立具有真实粗糙表面的实体,所以对有限元分析造成了较大的困难。应用Mathematica软件可以方便的产生三维粗糙实体,但是无法建立几何模型。为此利用在给定x、y步长的前提下,将所分析的表面利用式(1)进行离散生成Z(x,y)的坐标值,将x、y、Z(x,y)以空间坐标点云的形式输出。运用逆向软件Geomagic Studio处理点云数据生成三维粗糙实体几何模型。如图2所示(Geomagic软件具有强大的逆向功能,可以方便的处理点云数据生成较高质量的几何模型)。

图2 几何模型及有限元模型
Fig.2 Geometric model and finite element model
1.3 有限元模型
将图2导入ANSYS建立有限元模型,考虑到弹塑性及接触计算的复杂性做出如下假设:
(1) 认为滑动摩擦过程中,符合库伦定律,同时认为摩擦副的摩擦系数保持不变。
(2) 忽略材料磨损的影响,且认为动能全部转化为摩擦热而被摩擦副吸收。
(3) 三维粗糙实体(静环)、理想光滑刚体(动环)均为各向同性材料,材料的物理参数不随温度变化。
(4) 考虑摩擦热与应力耦合关系,假设粗糙实体与理想光滑刚体接触区域摩擦界面为理想热传导,即粗糙实体与理想光滑刚体接触区域界面对应点瞬时温度相等。
(5) 干气密封在启停阶段由干摩擦向气膜润滑转变,密封气体量较小,且启停阶段属于瞬态过程,温度不能及时由摩擦副传导至密封腔,因而不考虑摩擦副的对流换热以及热辐射。
第一步:在ANSYS中设置粗糙实体为弹塑性材料,设置率无关双线性等向强化模型(BISO模型)。第二步:考虑到滑动摩擦热力耦合分析,故选用SOLID226(20节点、六面体单元)耦合场单元,该单元为高阶单元,支持热-结构耦合分析,具有UX、UY、UZ、TEMP等自由度,支持材料的非线性,并且计算精度较高。第三步:将模型分配材料属性后划分网格,采用扫描方式划分网格,对网格层数进行控制,最终划分的网格如图2所示。第四步:同样为刚柔接触分析,因此需要在ANSYS软件中设置接触,所以选择CONTA174 (3D、8节点高阶四边形单元)3D面-面接触单元与TARGE170 3D目标单元。接触单元与目标单元通过相同的实常数号连接起来,面-面接触单元可用于任意形状的两个表面接触,两个面可以有不同的网格,支持大的滑动、大的应变和转动。因为接触过程存在滑动行为,所以设置标准接触行为,并设置闭合间隙、减小穿透。
1.4 位移及载荷边界条件
假设粗糙实体固定不动,理想光滑刚体沿(-x)方向滑动,如图2所示。考虑到粗糙实体的弹塑性变形,将三维粗糙实体四个侧面施加x、y方向的约束,同时将其上表面施加均布载荷p;将理想光滑刚体采用控制节点约束,约束其平动、转动自由度。
2 算例分析
2.1 材料参数
摩擦副中的粗糙实体(静环)采用M106K(浸锑石墨),理想光滑刚体(动环)采用YG8(硬质合金),粗糙实体与理想光滑刚体之间的摩擦因数取μ=0.15[17],具体材料参数见表2。
综合考虑干气密封动环从静环脱开的瞬态过程以及弹塑性、接触计算等非线性因素的复杂性,取动环滑动距离L=1 800 μm,在干气密封静环(粗糙实体)端面施加比载荷p=8 MPa,动环(理想光滑刚体)的转动速度v=3 m/s,设置初始温度为25 ℃,计算时设置两个载荷步,第一个载荷步加载均布载荷,第二个载荷步加载位移,编制ANSYS APDL命令流,采用ANSYS BATCH处理模式求解。
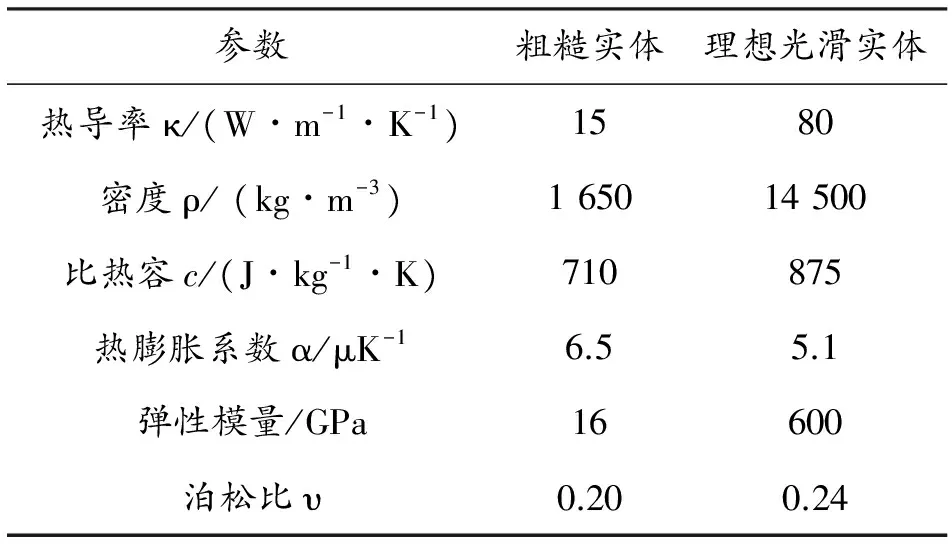
表2 摩擦副材料性能参数
2.2 分析与讨论
2.2.1 摩擦界面最高接触温度 摩擦界面最高接触温度随滑动时间变化曲线如图3所示。由图3可以看出,摩擦界面最高接触温度随滑动时间的增加呈逐步上升趋势,由25 ℃上升至65 ℃,并逐渐趋于平缓,在滑动摩擦期间最高接触温度呈现一定的波动性。

图3 摩擦界面最高接触温度随滑动时间变化曲线
Fig.3 Curve of the maximum contact temperature offriction interface with sliding time
在滑动的初始,由于摩擦副相对滑动速度从静止状态突然加速到3 m/s,使得摩擦界面最高接触温度急速上升,在t=1.5 μs时,摩擦界面的瞬时温度由初始温度25 ℃上升至45 ℃。45 ℃之后温升逐渐平缓,造成此种现象的原因为由于粗糙表面的微凸体凹凸不平、形状各异、滑动摩擦时只有极小部分的微凸体与理想光滑刚体接触,且微凸体接触区域并不连续,因而微凸体实际接触面积只占名义接触面积很小一部分,因此导致微小的外载荷就能产生较高的接触压力,而滑动摩擦所产生的热量大部分积聚于微凸体接触区域;在t=1.5 μs以后热传导逐渐发挥作用,使得积聚于微凸体的摩擦热向粗糙实体内部传递,从而导致微凸体最高接触温度有小幅度波动;在t=1.7 μs以后热传导作用越发明显,温升的波动性逐渐增加。但是,随着滑动摩擦时间的持续,热量逐渐在微凸体上产生、累积、传递,使得微凸体温度缓慢升高。同时,由于热传导作用使得微凸体周围温度有所升高,导致微凸体区域及粗糙实体内部温度上升梯度减小,因此最高接触温度的波动性逐渐平缓。从而推断出摩擦界面最高接触温升发生在初始阶段,随后缓慢增加。
2.2.2 粗糙表面VonMises应力场分布 粗糙表面VonMises等效应力分布如图4所示。由图4可以看出,粗糙表面的VonMises等效应力分布极其不均匀呈非线性变化规律,导致这种分布形态的原因是:粗糙表面不同微凸体其形状、大小均不同,所承受的载荷亦不同,与理想刚体接触时发生的弹塑性变形不同,以及温升膨胀等诸多因素的影响。因此使得接触微凸体VonMises等效应力分布呈非线性,微凸体接触区域中心至微凸体边缘区域VonMises等效应力值逐渐减小,同时微凸体接触区域中心VonMises等效应力值远大于微凸体接触边缘区域VonMises等效应力值。
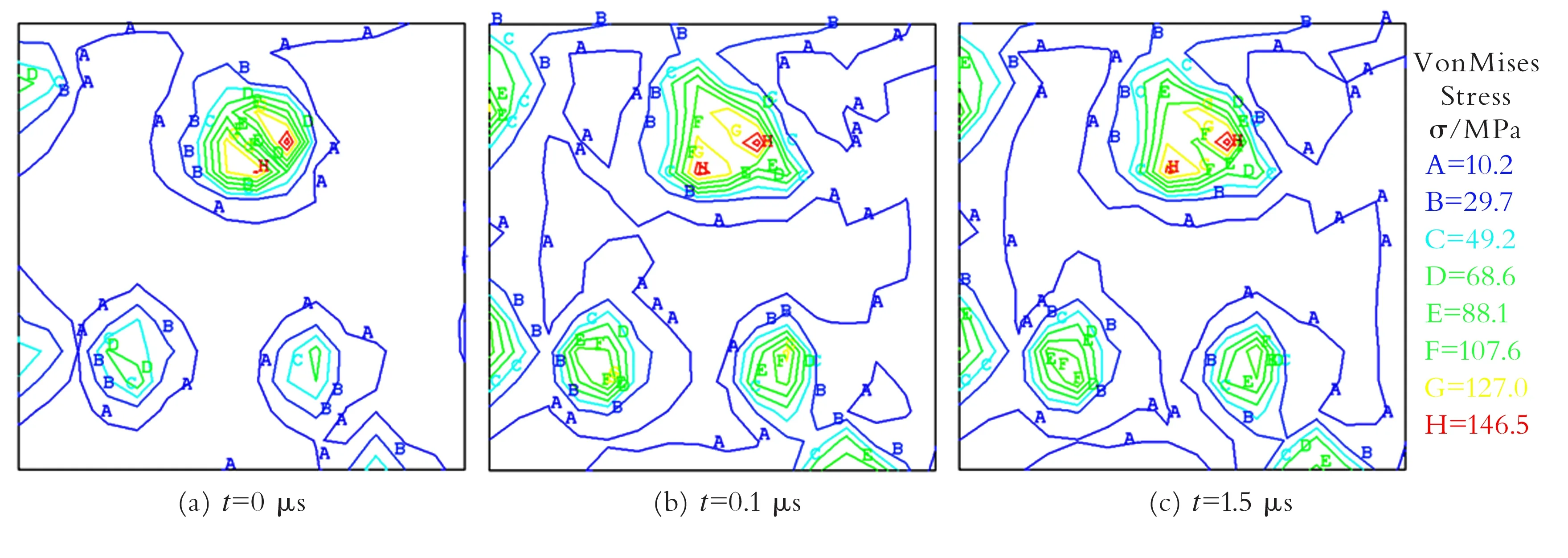
图4 不同时刻粗糙表面VonMises等效应力等值线
Fig.4 Contour plot of VonMises equivalent stress of rough surfaces with different time
加载结束,在理想刚体滑动的一瞬间(t=0.1 μs),粗糙表面微凸体接触区域VonMises等效应力值增大了,这是由粗糙表面微凸体发生了弹塑性变形、热应力及摩擦界面的剪切所导致。在滑动时间t=1.5 μs时,粗糙表面微凸体接触区域VonMises等效应力值有所降低,这是因为粗糙表面微凸体接触区域的温度急速升高,微凸体接触区域发生了膨胀,使得较小微凸体相互作用变成较大的微凸体,导致微凸体接触面积增大,此时加载已结束,外载荷保持不变,因此微凸体接触区域VonMises等效应力值下降,从而可以推断出理想刚体滑动瞬间粗糙表面微凸体接触区域快速升温时,粗糙表面微凸体接触区域VonMises等效应力值变化较大。
2.2.3 微凸体接触区域x方向应力分量σxx随粗糙实体厚度变化曲线 粗糙实体与理想光滑刚体发生相对位移时,微凸体周围的应力分布纷繁复杂,其数值大小及分布形态对整个摩擦过程影响巨大,尤其是沿着滑动方向的应力对裂纹的萌生及扩展起着重要作用。
在整个滑动摩擦模拟的过程中发现最大x方向的应力σxx并未出现在最高接触微凸体(节点656)上,而是出现在最高接触微凸体后方离光滑表面5.1 μm的节点349上,其x方向应力值大约为23 MPa。因此以节点349作剖面图,做出最大x方向应力σxx随三维粗糙实体厚度(z轴方向)的变化曲线图,如图5所示。图5中t=0 μs,t=0.1 μs及t=1.5 μs分别表示加载结束后开始滑动前、滑动的一瞬间以及快速升温后的不同滑动时刻。

图5 不同滑动时刻三粗糙实体x方向应力分量σxx随厚度变化曲线
Fig.5 Variation of three-dimensional rough solid with thicknessdirectionσxxconsidering different sliding time
由图5可以看出,三维粗糙实体从粗糙表面到光滑表面,随着三维粗糙实体厚度的增加,x方向最大应力σxx从压应力逐渐变为拉应力,最后变为压应
力。但在整体变化过程中,大部分属于压应力,且数值波动不大,从而也验证了滑动摩擦区域中存在拉应力区[18-19]。
微凸体在外载荷的作用下,发生弹塑性变形,在微凸体受载逐渐被压平的过程中,同时伴随着微凸体向四周膨胀。因此微凸体接触区域显示为压应力。由于三维粗糙实体不同厚度材料的弹塑性变形量不同,从而使得x方向应力分量σxx很快由压应力变为拉应力。在加载结束的,理想光滑刚体尚未滑动的时刻(t=0 μs),同样由于上述原因,拉应力区域大约位于距三维粗糙实体粗糙表面0.5 ~1.6 μm。在理想光滑刚体滑动的瞬间(t=0.1 μs)以及接触微凸体区域快速升温(t=1.5 μs)导致微凸体接触面积以及微凸体接触数量均发生明显变化,从而使得这一拉应力区域厚度有所增加,拉应力区域σxx值增大。由此可以推断出,理想光滑刚体滑过三维粗糙实体时,粗糙实体最大x方向应力分量σxx位于粗糙实体后方距光滑表面一定距离处,此时粗糙实体这一区域将遭受循环拉-压应力作用,若这一区域材料存在缺陷,则滑动摩擦过后此区域可能造成裂纹的萌生。
3 结 论
(1) 粗糙表面微凸体接触区域的VonMises等效应力分布极其不均匀,呈非线性变化,微凸体接触区域中心至微凸体边缘区域的VonMises等效应力值逐渐递减,并且微凸体接触区域中心VonMises等效应力值远大于边缘区域VonMises等效应力值。这是由于粗糙表面不同微凸体其形状、大小均不同,所受的载荷亦不同,与理想光滑刚体接触时发生的弹塑性变形不同以及温升等诸多因素。
(2) 在整个滑动摩擦模拟的过程中发现最大x向的应力σxx并未出现在最高接触微凸体上,而是出现在微凸体后方一定深度处。表明当理想光滑刚体滑过三维粗糙实体粗糙表面时,粗糙实体最大x方向应力位于接触微凸体之后的粗糙实体光滑表面下方。导致这种现象原因为三维粗糙实体厚度方向材料弹塑性变形不同。
(3) 根据文中的研究结果可以推断出:若动静环材料存在缺陷,必然在两端面滑动摩擦的过程中造成裂纹的萌生,严重时破坏动静环的工作状态。
(4) 由于本文并未考虑密封气体对摩擦热的影响,基于此,今后研究工作将密封气体对摩擦温升的影响这一不稳定的流场考虑进去。
[1] Archard J A. Elastic deformation and the laws of friction [J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1957,243(1223):190-205.
[2] Greenwood J A, Trip J H. The elastic contact of rough spheres[J]. Journal of Applied Mechanics, 1967,34(1):153-159.
[3] Greenwood J A, Williamson P. Contact of nominally flat surfaces[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,1966, 295 (1442):300-319.
[4] Majumadr A, Bhushan B. Fractal model of elastic-plastic contact between rough surfaces[J]. ASME Journal of Tribology, 1991, 113(1):1-11.
[5] 孙见君,顾伯勤,魏龙.基于分形理论的接触式机械密封泄漏模型[J].化工学报,2006,57(7):1626-1631. Sun Jianjun, Gu Boqin, Wei Long. Leakage model of contacting mechanical seal based on fractal geometry theory[J]. Journal of Chemical Industry and Engineering(China), 2006,57(7):1626-1630.
[6] 魏龙,顾伯勤,冯秀,等.机械密封摩擦副端面接触分形模型[J].化工学报,2009, 60(10):2543-2548. Wei Long, Gu Boqin, Feng Xiu, et al. Contact fractal model for friction faces of mechanical seals[J]. Journal of Chemical Industry and Engineering(China), 2009, 60(10):2543-2548.
[7] 魏龙,刘其和,张鹏高.基于分形理论的滑动摩擦表面接触力学模型[J].机械工程学报,2012, 48(17):106-113. Wei Long, Liu Qihe, Zhang Penggao. Sliding friction surface contact mechanics model based on fractal theory[J]. Journal of Mechanical Engineering, 2012, 48(17):106-113.
[8] 朱维兵,王和顺,徐昌学,等.机械密封热变形研究进展[J].机械设计与制造,2011(12):267-268. Zhu Weibing, Wang Heshun, Xu Changxue, et al. Researching progress in thermal deformation of mechanical seal[J]. Machinery Design and Manufacture, 2011(12): 267-268.
[9] Pascovici D, Etsion I. A thermo-hydrodynamic analysis of a mechanical face seal[J]. Journal of Tribology, 1992,114(4): 639-645.
[10] Etsion I, Groper M. The accuracy of analytical solution for the temperature distribution in mechanical face seals[C]// 14th International Conference on Fluid Sealing. Firenze, Italy:[s.n.].1994: 341-350.
[11] 朱孝平,汪久根,周桂如.机械密封端面温度简化计算模型[J].流体机械,1995, 23(9):31-36. Zhu Xiaoping, Wang Jiugen, Zhou Guiru.Simplifed calculation model of mechanical seal end face temperature[J]. Fluid Machinery, 1995, 23(9): 31-36.
[12] 周剑锋,顾伯勤.机械密封环的传热特性分析[J].机械工程学报,2006, 42(9):201-206. Zhou Jianfeng, Gu Boqin. Heat-transfer character analysis of rings of mechanical seal[J]. Journal of Mechanical Engineering, 2006,42(9): 201-206.
[13] 高杰,宋鹏云,马方波,等.机械密封端面温度近似解析计算的新方法[J].润滑与密封,2012,37(4):48-52. Gao Jie, Song Pengyun, Ma Fangbo, et al. A new approximate analytical method for calculating the face temperature of mechanical seals[J]. Lubrication Engineering, 2012,37(4): 48-52.
[14] 葛世荣,朱华.摩擦学的分形[M].北京:机械工业出版社,2005.
[15] 姬翠翠,朱华.粗糙表面分形接触模型的研究进展[J].润滑与密封.2011,36(9):114-119. Ji Cuicui, Zhu Hua. Research progress on M-B fractal contact model[J]. Lubrication Engineering, 2011,36(9): 114-119.
[16] 丁雪兴,严如奇,俞树荣,等.接触式机械密封摩擦端面接触状态的仿真分析[J].兰州理工大学学报,2015,41(3):45-48. Ding Xuexing, Yan Ruqi, Yu Shurong, et al. Simulation and analysis of contact state of friction end-face in contacting mechanical seals[J]. Journal of Lanzhou University of Technology, 2015,41(3): 45-48.
[17] 顾永权.机械密封的摩擦系数与工况参数[J]. 石油大学学报(自然科学版),1991,15(3): 71-83. Gu Yongquan. Friction coefficient of mechanical seal and working parameters[J]. Journal of Petroleum University(Natural Science Edition), 1991,15(3): 71-83.
[18] 李建明.磨损金属学[M].北京:冶金工业出版社,1990.
[19] 邵荷生,曲敬信,许小椂,等.摩擦磨损[M].北京:煤炭工业出版社,1992.
(编辑 王亚新)
A Numerical Simulation Study of Frictional Characteristics of Seal Faceson the Starting and Stopping Process of a Dry Gas Seal
Ding Xuexing, Wang Wending, Jin Haijun, Zhao Haihong
(SchoolofPetrochemicalEngineering,LanzhouUniversityofTechnology,LanzhouGansu730050,China)
The starting and stopping processes play an important role in reduce friction and abrasion of a spiral groove dry gas seal. Thus, the startup and shutoff of the seal is investigated by a numerical approach. The computational procedure based on the material properties of rotational and stationary rings, interaction of micro asperity, and frictional heat-flow coupling is implemented to build a three-dimensional thermo-mechanical coupling model considering sliding friction within rough-rigid body. And then, the ANSYS software is used to simulate the friction heat and the stress variation of rough-rigid body based on the characteristics of nonlinear multiphysics. The results are presented, and it shows that the maximum contact temperature value of the roughened surface increases with increase in the sliding time and presents a little fluctuation, and the distribution of VonMises equivalent stress is extremely non-uniform and non-linear. What’s more, the stress component of maximumx-direction(σxx) isn’t appeared in the region of highest contact asperity. The results reveal that a tensile stress is existed along the thickness direction of three-dimensional rough solid and the region of tensile stress is enlarged slightly with the sliding time. According to above results, it can be shown that increase in temperature and fluctuation are attributed to thermal conduction caused, the change of stress is due to the elastic-plastic deformation of asperities. These results illustrate the potential of numerical simulation in prediction the temperature and stress of seal faces during the starting and stopping process and may help in the design and optimization of spiral groove dry gas seal.
Dry gas seal; Asperity; Sliding friction; Elastic-plastic deformation; Temperature rise; Stress
2017-01-11
2017-02-03
丁雪兴(1964-),男,博士,教授,从事流体密封动力学、摩擦学研究;E-mail:xuexingding@163.com。
王文鼎(1992-),男,硕士研究生,从事摩擦学研究;E-mail:wendinglut@126.com。
1006-396X(2017)02-0091-06
投稿网址:http://journal.lnpu.edu.cn
TE964; TQ051
A
10.3969/j.issn.1006-396X.2017.02.017

