一种单输入输出系统可控发射结果的仿真方法

沈 昊， 陈 良

1. 宝钢不锈钢股份有限公司 上海 200431 2. 上海宝信软件股份有限公司 上海 201203

1 问题的产生

在单输入输出系统的工业应用中，人们常常遇到这样的情况： 对于输入端的时序序列是完全可控的，但对于输出端能输出什么样的时序序列却不能马上知晓。为了得到符合预定要求的输出，只有通过不断假设输入、测量、调整输入，最后得到满意的输出[1]。

比如在某些声波测量的应用中，需要对发射出的脉冲波形进行特殊控制，又比如对一个复杂信号通过某个滤波器后的信号波形进行预测，都会遇到同样的问题[2]。

在一些工业应用中，需要反复进行输入试验，才能取得较好的输出效果。这样不仅浪费时间和资源，还难于总结规律。笔者提出一种单输入输出系统可控发射结果的仿真方法，如图1所示。

图1 典型单输入输出系统示意图

2 可控发射仿真依据

工业应用中的单输入输出系统大多可以简化为线性系统。在描述单输入输出线性系统的微分方程中，无论是因变量或是其导数，都不高于一次方，并且没有一项是因变量与其导数的乘积[3]。

定义系统在输入x(t)作用下输出为y(t)，记为[4]：

x(t)→y(t)

(1)

由于线性系统的齐次性与叠加性，以及物理系统的时移不变性[5]，以下关系成立：

jx(t+t0)→jy(t+t0)

(2)

式中：j为常数；t0为某给定时间。

由于工业应用中，输入输出均为数字化的呈现方式，因此将以上原理进行离散化处理[6]，以适用于工程计算。

对式(1)以某一适合频率f进行采样，即令t=n/f(n=0，1，2，3…)，得到数列X(n)、Y(n)，记为：

X(n)→Y(n)

(3)

对式(2)而言，同样成立以下关系：

jX(n+m)→jY(n+m)

(4)

式中：m为0与整数。

当j=1时，得到式(4)的特殊形式，体现了时移不变性，记为：

X(n+m)→Y(n+m)

(5)

当m=0时，得到式(4)的特殊形式，体现了线性，记为：

jX(n)→jY(n)

(6)

定义X(n)=[1,0,0,0…]为X(n)0，其输出数列Y(n)=[Y1(0)，Y1(1)，Y1(2)，Y1(3)…]为Y(n)0。根据经典控制理论，X(n)0对应的输出数列Y(n)0可类比为系统的单位脉冲响应，其拉普拉斯变换即为系统传递函数[7]。

由于X(n)输入信号总能量与X(n)数列平方和成正比[8]，X(n)0、Y(n)0的信号能量很小，在工业应用中对Y(n)0直接测量比较困难，因此常根据式(6)用jX(n)0(j为较大的值)进行测量，再根据式(6)，将输出结果除以j，得到Y(n)0。

当jX(n)0能量依然有限时，通过阶跃响应、斜坡响应的结果来做一次、二次求导得到Y(n)0，也是实际中常用的方法[9]。

不难得出，当输入序列为X(n)=[a,b,c,d…]时，基于Y(n)0，通过式(5)、式(6)得到：

Y(n)=aY(n)0+bY(n+1)0+
cY(n+2)0+dY(n+3)0…

(7)

式中：a、b、c、d为任意有理数。

3 应用实例

在上海宝钢集团不锈钢热轧轧辊超声波测量项目中，期望在超声波发射中发出一个带尖锐突出下沿的超声波信号。实际情况是，由于测量项目中的声发射器需要承受很大的功率，其频带宽度有限，难以直接形成带有高出平均值3dB以上尖锐下沿的原始波形。

由于声发射器输入端的波形是可控的，笔者根据式(6)用jX(n)0取得了jY(n)0，项目中j实际取值为255。

使用jY(n)0反求得到Y(n)0后，对数列Y(n)0数据进行归一化。数列长度150，取值范围(-255～255)，单位脉冲响应数列Y(n)0如图2所示。

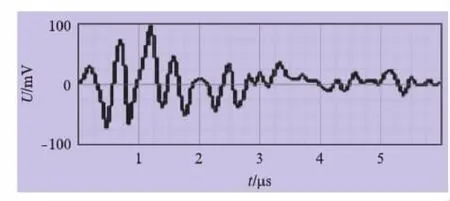
图2 声发射器输入端单位脉冲响应数列波形

以Y(n)0作为基础，依据式(7)的原理编写了一个应用程序。该应用程序可以根据式(6)提供的任意X(n)数列实时计算并显示仿真的Y(n)。

在计算机的应用程序中进行试凑，当X(n)为试凑序列X(n)1时，实时显示预测的Y(n)1如图3所示，显然满足高出平均值3dB以上尖锐下沿的需求。

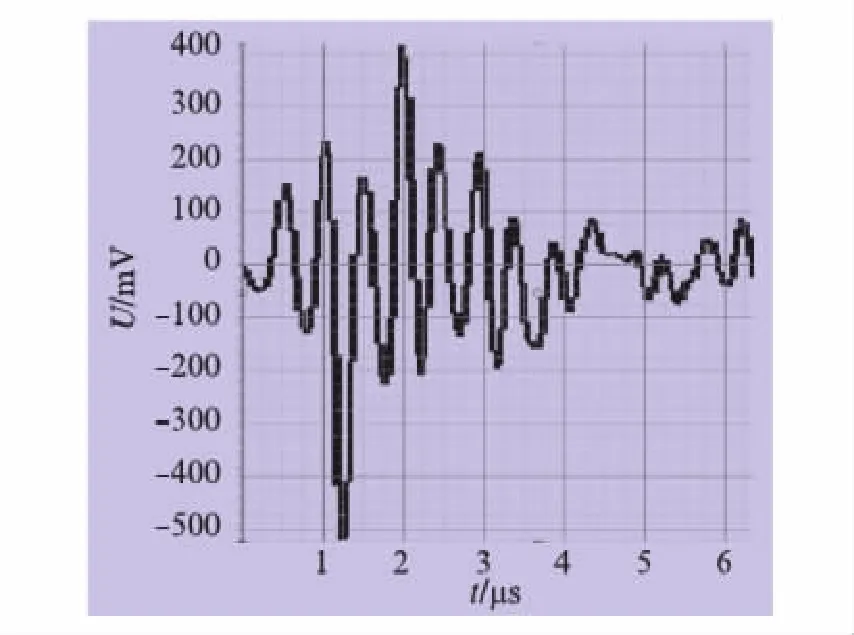
图3 试凑计算机仿真波形

在宝钢集团不锈钢热轧轧辊超声波测量项目中，将X(n)1作为实际的声发射器输入端波形，激励出的超声波信号实测如图4所示。

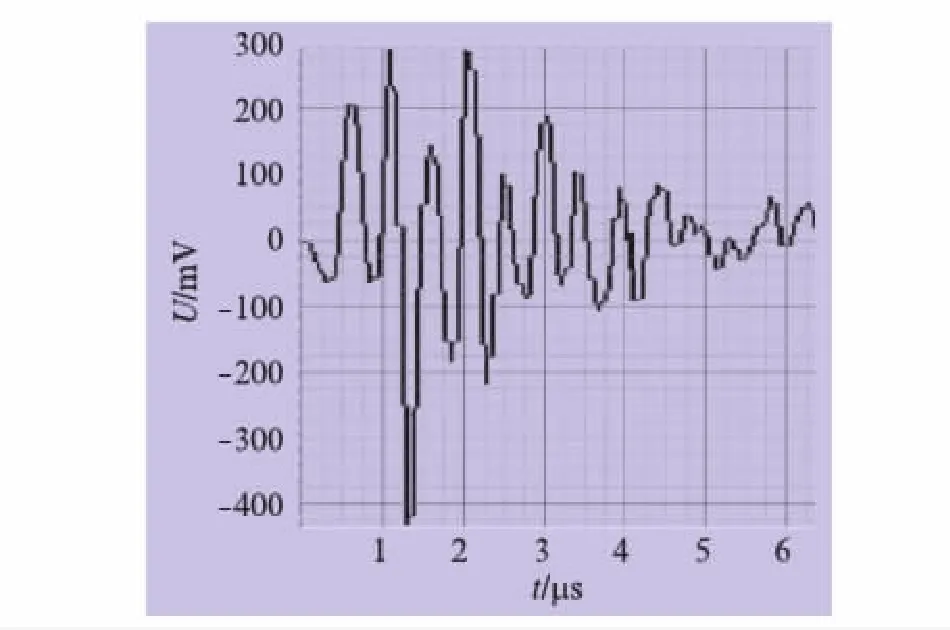
图4 实测超声波波形

比较图3和图4可以看出，预测值与实际值非常近似，部分差异是由于系统被近似为线性系统所引起的误差[10]。

4 应用延伸

通过对宝钢集团不锈钢热轧轧辊超声波测量项目的仿真结果进行对比，证明笔者所述仿真方法是正确有效的。

另一方面，根据所述方法，也可以在多输入单输出线性系统中对每个输入通道进行测量，取得每个通道的单位脉冲响应Y(n)0，然后对各个通道进行线性叠加仿真。

利用所述方法，可以避免大量试验流程，并快速得到仿真结果，节约资源。

[1] 郑大钟.线性系统理论[M].北京： 清华大学出版社，1990.

[2] 刘豹.现代控制理论[M].北京： 机械工业出版社，1983.

[3] 胡寿松.自动控制原理[M].5版.北京： 科学出版社，2007.

[4] 谢克明.现代控制理论[M].北京： 清华大学出版社，2007.

[5] 赵光宙.现代控制理论[M].北京： 机械工业出版社，2010.

[6] 谢亚军.浅析经典控制理论与现代控制理论的异同[J].科学财富，2013(5)： 136-137.

[7] 周立峰.现代控制理论的发展与应用研究[J].大自然探索，1984(3)： 29-35.

[8] 董景新，赵长德.控制工程基础[M].北京： 清华大学出版社，1992.

[9] 贺良华.现代控制理论及应用[M].武汉： 中国地质大学出版社有限责任公司，2013.

[10] 王凡，王思文，郑卫刚.现代控制理论概述及实际应用意义[J].网友世界，2012(13)： 59-61.