基于有限控制集的感应电机直接相角预测控制研究

罗小丽，陈意军，刘万太，李谟发

(1.湖南电气职业技术学院，湘潭 411101；2.湖南工程学院，湘潭 411101)

0 引 言

对于感应电机的控制策略，趋于成熟的传统控制方法有磁场定向控制(以下简称FOC)和直接转矩控制(以下简称DTC)[1-2]。但是随着数字芯片技术的发展，越来越多计算密集型的智能控制，诸如模糊控制、滑模控制和神经网络控制等得到广泛研究[3-5]。而预测控制技术由于其较之传统控制有更快的动态响应和精确的稳态性能也得到了快速发展[6-10]。

目前2种主要的预测控制方法是无差拍控制和模型预测控制(以下简称MPC)[11-18]。无差拍控制是在离散系统下通过计算来对参考量进行精确的单步长跟踪实现的，但是其对参数变化的鲁棒性较差，因为在计算中难以考虑逆变器自身的离散特性[11-12]。MPC是基于一个包含了各种对参考量跟踪判断的代价函数实现的，其基本原理是通过计算使得代价函数值最小化来输出控制开关矢量对电机进行控制。根据不同的计算过程，MPC算法分为广义预测控制(以下简称GPC)[13-14]和有限控制集模型预测控制(以下简称FCS-MPC)[15-20]。对于GPC算法，代价函数最小化是基于综合自回归滑动平均模型CARIMA实现的，包含大量计算，这显著降低了工程应用范围[13-14]。而FCS-MPC方法考虑了逆变器的离散性，代价函数最小化计算过程较GPC算法简单，因而容易实现，可行性高，解决了传统DTC算法高转矩脉动的缺点，但是较传统FOC算法效率低，尤其是轻载时，这是因为FCS-MPC算法中代价函数仅代表转矩和磁链误差。针对这个问题，文献[19]将电流限制和最大转矩电流比判据增加到了代价函数，以期提高控制效率，而文献[20]将电压最小化判据增加到了代价函数，以限制电机高速运行时的电压。但这些方法的判据都是基于磁场定向，因而需要旋转坐标变换，从而旋转角的误差将导致精度降低，而且同时需要3个判据添加到代价函数中，这将增加计算量，复杂度甚至远远超过传统的FOC算法。

本文在前述文献研究的基础上，设计了一种新型的基于有限控制集的感应电机直接相角预测控制，其将磁场定向原理嵌入到预测DTC算法中，只在代价函数中增加了一个新型旋转角控制判据，而没有使用直接的磁链控制，同时为了达到精准的控制效果，还设计了闭环预测模型。最后通过搭建试验平台对新型控制策略进行了试验验证。

1 直接相角预测控制算法

1.1 基本原理

传统的FCS-MPC控制基本原理是基于代价函数最小化。而代价函数最小化主要是基于将转矩和磁链误差最小化，具体执行即将所有的可行状态代入到代价函数中进行计算，选取使得代价函数小的最优状态输出。一般转矩和磁链的关系可描述：

(1)

式中：T为电磁转矩；λs为定子磁链矢量；Is为定子电流矢量；αs是定子电流和磁链之间的相角；p为极对数。在传统控制方法中，定子磁链被控制为恒定值，从而调节|Is|和sinαs可以达到控制转矩的目的。由于固定磁链最优时，将通过控制电流和sinαs来调节转矩，从而可能导致电流幅值达不到最优，而且另外一方面最优磁链的计算过程较为复杂。

根据上述分析，本文提出了一种新的FCS-MPC控制方案，即调节电流相位角以最大限度地减少电流幅值，同时转矩控制将自动对磁链进行优化。为了计算定子电流的相位角，将转矩方程重新写为转子磁链和定子电流的函数如下：

(2)

式中：λr为转子磁链矢量;Lr和Lm分别是转子电感和互感;αr是定子电流和转子磁链之间的相角。上式还可以在转子磁场定向坐标系下写成：

(3)

式中：λr=λrd′，转子磁链的q轴分量为0。另一方面，在转子磁场定向坐标系下的d轴转子方程：

(4)

式中：Rr为转子电阻；ωs和ωr分别是同步角频率和转子角频率。考虑到磁场定向后等式右边为0，而稳态时转子磁链的导数近似为0，故有：

Ird′=0

( (5)

从而转子磁链可通过下式计算：

λr=LmIsd′

(6)

将式(6)代入式(3)，可以得到转矩与定子电流d,q分量乘积成正比的关系式如下：

(7)

从上式中可以推导出恒定转矩下，定子电流的轨迹是一个双曲线，另一方面，定子电流幅值恒定的轨迹是一个圆，具体如图1所示，当定子电流与转子磁链之间的相位角为45°时，将生成最小电流幅值。图1即为基于直接相角预测控制的FCS-MPC算法基本矢量原理图。

图1 直接相角预测控制的基本原理图

1.2 代价函数设计

FCS-MPC算法具体的实现过程是通过遍历所有可执行状态，选择一个使代价函数最小化的状态。下式给出了新型FCS-MPC控制策略的代价函数，其是以确保转矩控制和电流最小化设计的。

(8)

2 闭环预测模型

2.1 模型推导

为了计算不同状态时的代价函数值，需要预测下一个步长的转矩和相角，这就需要建立预测模型。三相异步感应电机的数学模型方程式如下[6]：

(9)

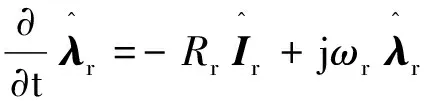
( (10)

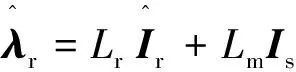
(11)

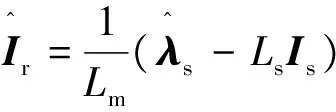
(12)

对上述方程采用欧拉方法进行离散化处理并进行推导可以得到：

(13)

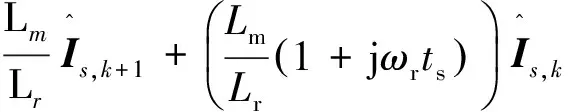
(14)

将式(12)代入式(14)可以得到：

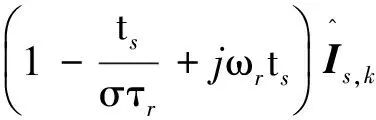
(15)

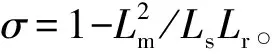
(16)

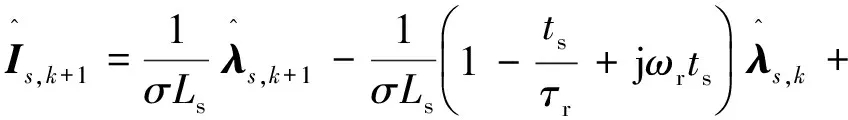
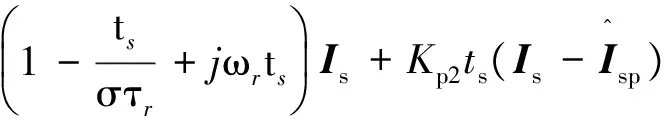
( (17)

( (18)

另一方面，磁通和电流的关系式：

(19)

由式(18)和式(19)可推导出转子磁链预测方程：

( (20)

上式表明，下个步长的转子磁链与矢量状态的选择无关，故矢量状态的选择仅仅决定了代价函数里的定子电流幅值和相角，这提高了算法的鲁棒性，即矢量状态的选择仅仅通过定子电流矢量影响转矩，具体如下：

(21)

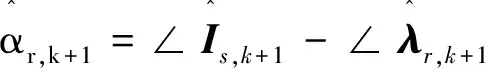
(22)

图2为闭环预测模型的框图，它描述了当前步长状态观测器估计磁链的过程。图3为新型直接相角预测控制算法的框图，可以注意到状态观测器框图与预测模型框图相似，但转矩和转子磁链估计是不需要在观测器模型中进行的，因此式(16)、式(17)应被延迟使用。图4给出了所提出的方法的具体计算流程图。

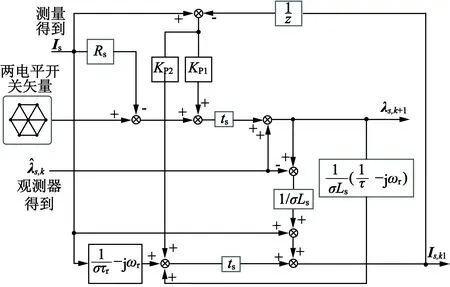
图2 闭环预测模型的框图

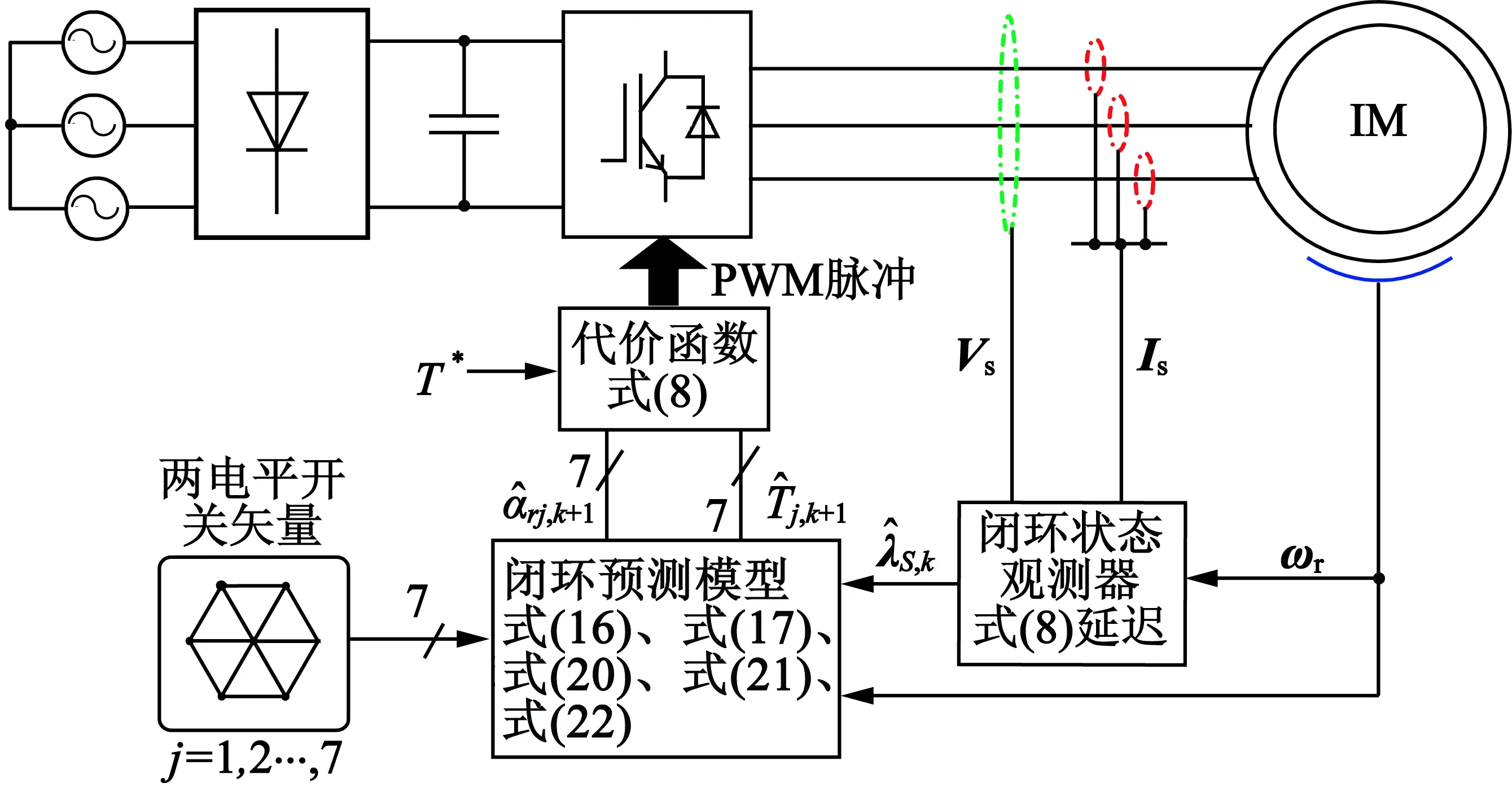
图3 直接相角预测控制示意图

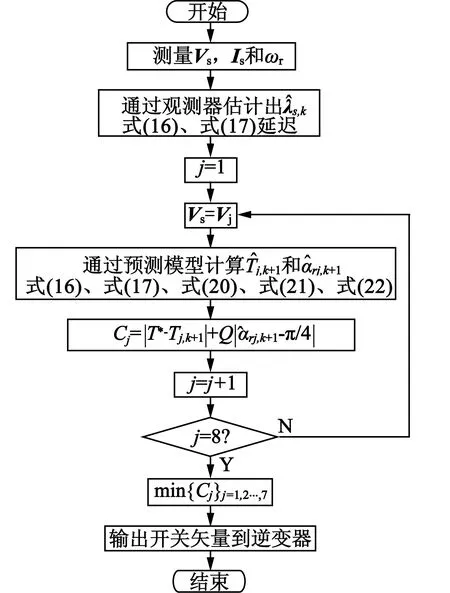
图4 新型控制策略的流程图

2.2 反馈增益设计

增加闭环预测模型的反馈设计可提高整个算法的鲁棒性，但同时也需要对反馈增益进行计算。本文针对反馈增益设计，使用了一种较简单的极点转移方法[22]。注意到速度是测量得到的，为了平衡预测模型的快速性和稳定性，将使用H-∞鲁棒性方程确定转移值ksh。式(12)、式(13)中的反馈增益是复数形式，具体：

(23)

计算增益的实部和虚部，以转移预测模型的极点，如下所示：

(24)

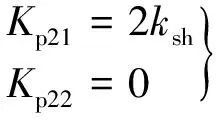
( (25)

式中：a1=(1/τr-jωr)/σLs，a2=-1/στs-1/στr+jωr。

为了确定ksh，应将闭环预测模型的离散传递函数的H∞范数最小化。

(26)

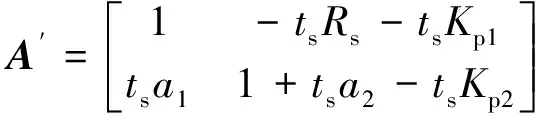
( (27)

(28)

(29)

通过解下面的方程，可以得到式(19)的次优解：

‖C(zI-A′)-1B‖

(30)

( (31)

将电机相关参数代入进行计算，考虑定转子电阻，式(30)右侧为0.084 47，因为矩阵A′取决于转速变量，因此需要在一个固定的转速下求解，通过对低速范围内计算，推导出ω=50 r/min(3%额定同步转速)是使得式(30)有解的最低速度。图5为当转移值ksh从50变化到100时的闭环传函无穷范数H∞的变化曲线，随着转移值的增加，无穷范数减小。为了避免过大的转移值减缓预测模型的计算速度，设置转移值为72。然后在离散模型中计算后的增益需要和ts=100 μs相乘。在离散时间域内闭环模型的特征值在单位圆以内，分别为0.884 3±j0.000 1和0.875 6±j0.000 1。如果采样时间增加，闭环传

图5 H无穷范数随转移值ksh变化曲线

函将降低精度，因此限制采样时间为1.607ms,以保持极点在单位圆内。

2.3 电机起动设计

由于新型控制策略没有采用直接的磁链控制，因此在电机初始起动阶段不能保持转矩为0而增加磁链，因此需要对起动过程进行预充磁设计。在预充磁过程中将相角参考值设置从45°改为0°，从前面图1中可以看出，零相位角可以在转矩为零的同时增加磁链，即预充磁，同时此过程中将不使用零状态矢量，然后当磁链达到标称值时即退出预充磁过程，以避免磁饱和，接着控制器转入到正常控制模式。具体的预充磁起动过程的代价函数：

(32)

3 试验验证

为了验证这种新型的基于有限控制集的感应电机直接相角预测控制方法，搭建了如图6所示的试验平台并开展了相关试验研究，其中控制器芯片采用TI公司的DSP28335芯片，变频器采用集成驱动模块PM15CZF120实现。主要的试验系统相关构成参数如表1所示。

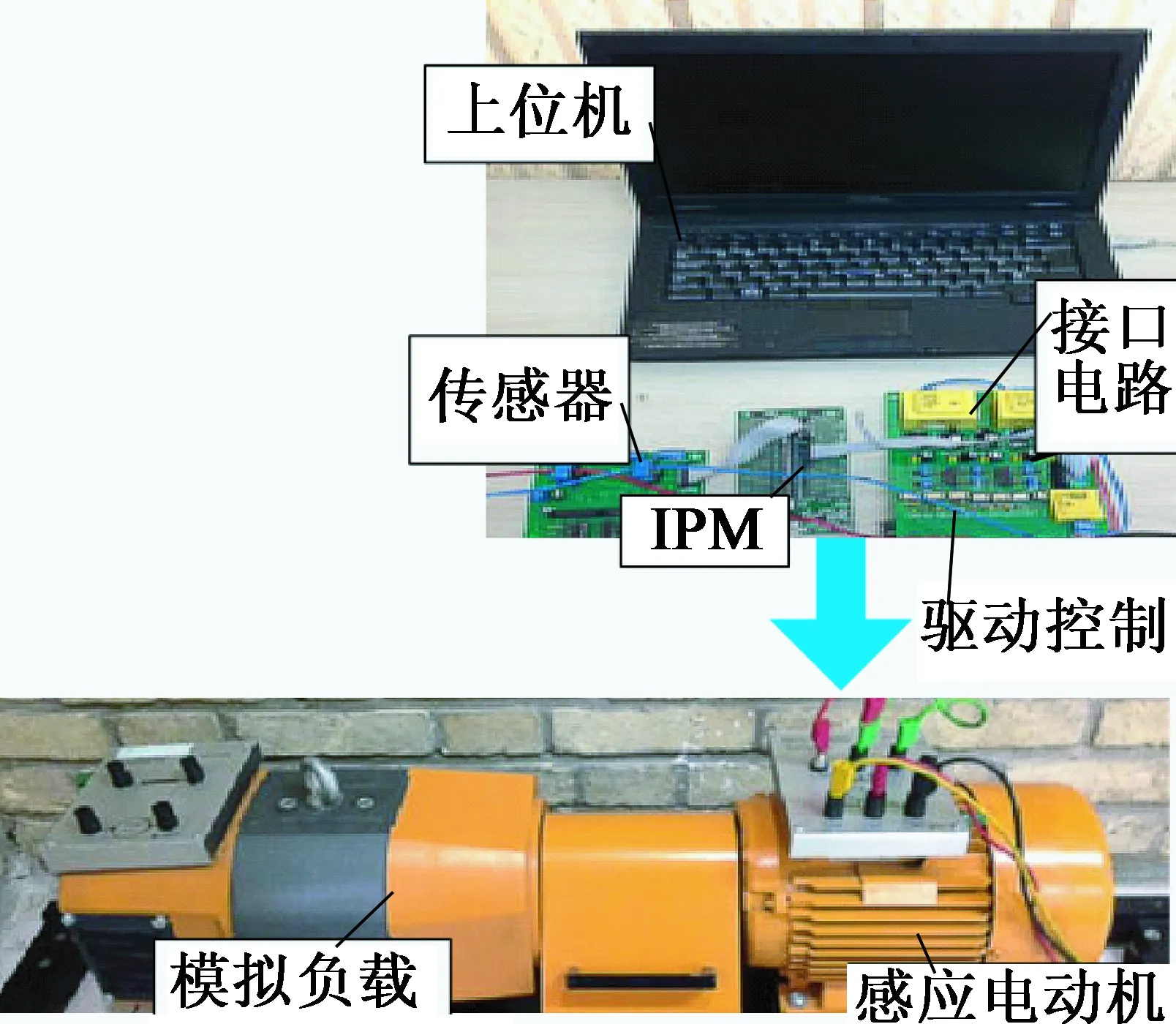
图6 试验平台构成

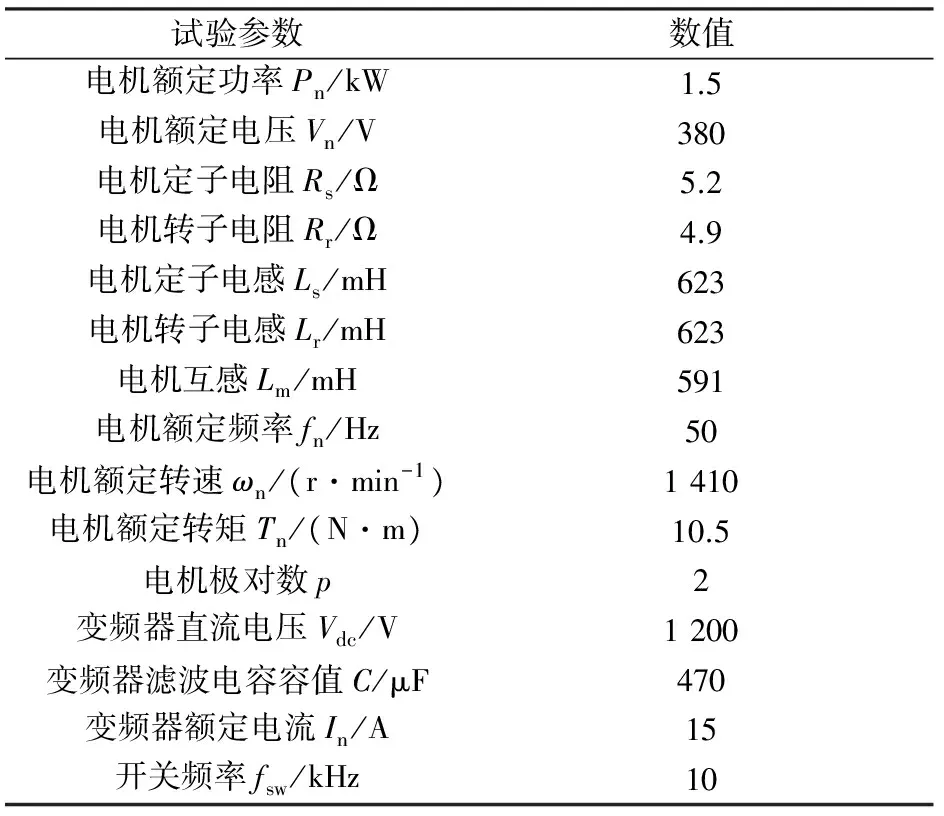
试验参数数值电机额定功率Pn/kW1．5电机额定电压Vn/V380电机定子电阻Rs/Ω5．2电机转子电阻Rr/Ω4．9电机定子电感Ls/mH623电机转子电感Lr/mH623电机互感Lm/mH591电机额定频率fn/Hz50电机额定转速ωn/(r·min-1)1410电机额定转矩Tn/(N·m)10．5电机极对数p2变频器直流电压Vdc/V1200变频器滤波电容容值C/μF470变频器额定电流In/A15开关频率fsw/kHz10

图7为在50%额定负载转矩和50%额定转速参考下的电机控制效果波形。从图7中可以看出,在起动过程中，相角保持为0°进行预充磁，此后进入到模型预测控制，相角稳定控制在45°。

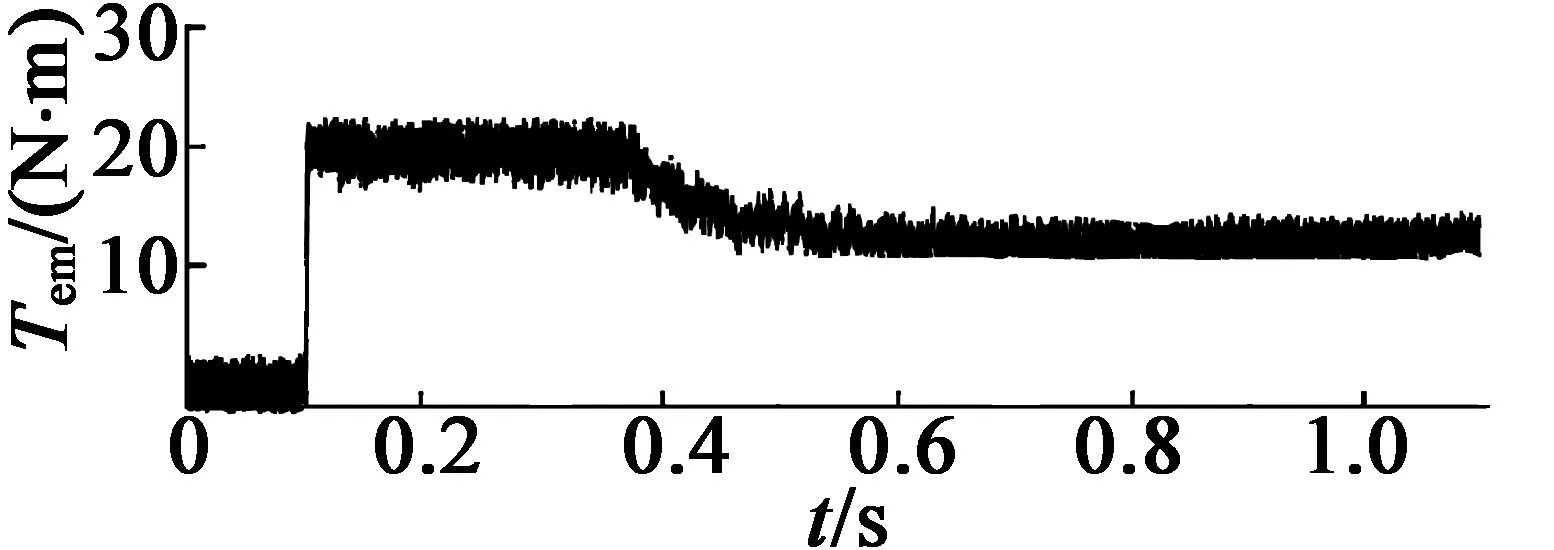
(a) 电磁转矩波形

(b) 相角波形

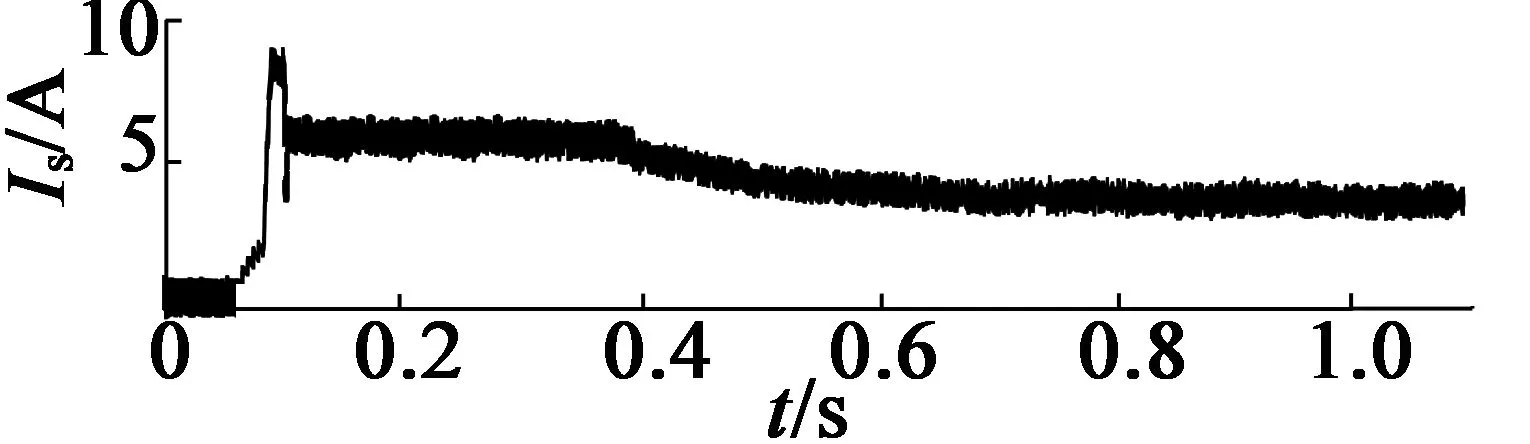
(c) 定子电流波形

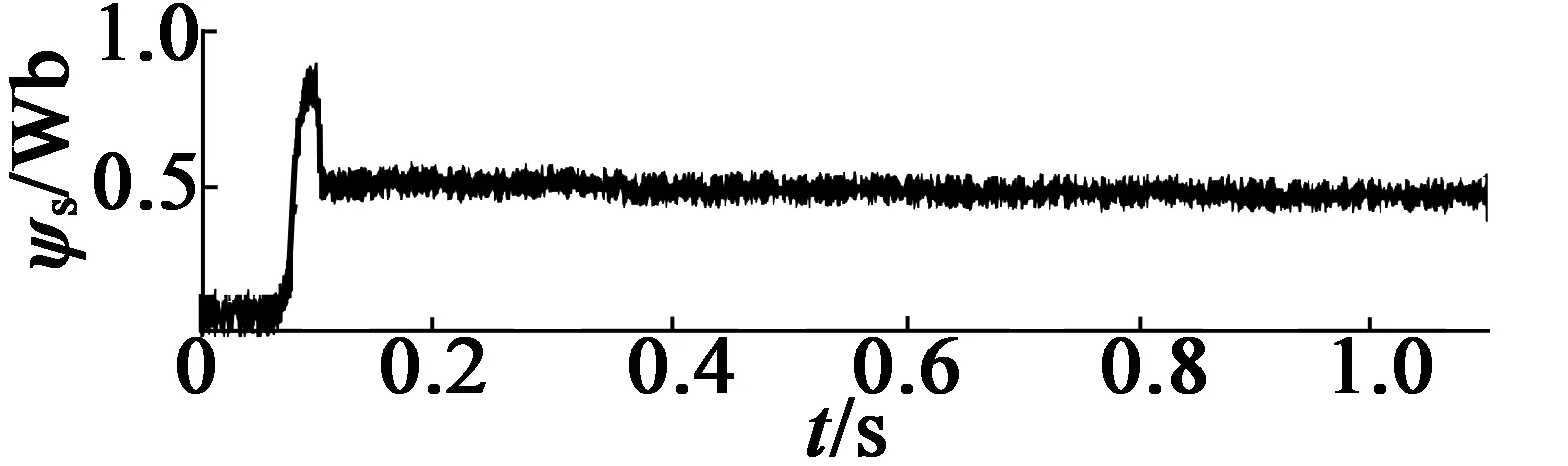
(d) 定子磁链波形

图8为电机的低速性能试验波形。此时设置负载转矩为50%额定转矩，速度设置为5%额定转速。从图8中可以看出，电机在低速时的磁链波动动态较之前高转速时明显，这是因为起动转矩需要较大磁链。

(a) 转速波形

(b) 电磁转矩波形

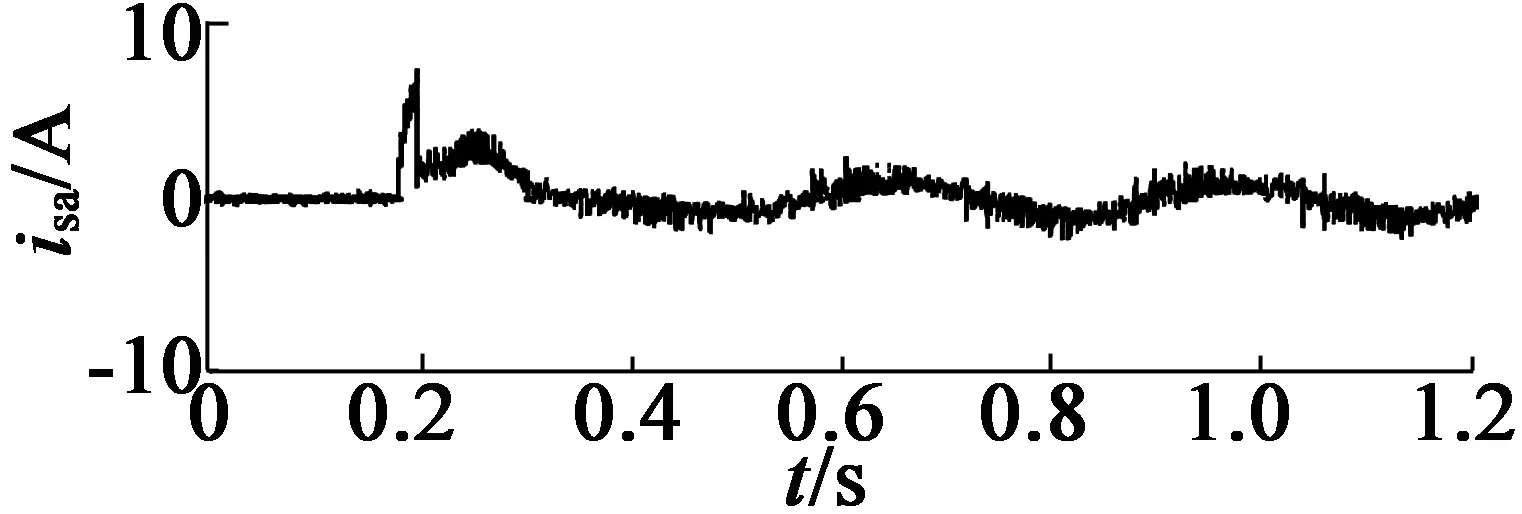
(c) 定子电流波形

(d) 定子磁链波形

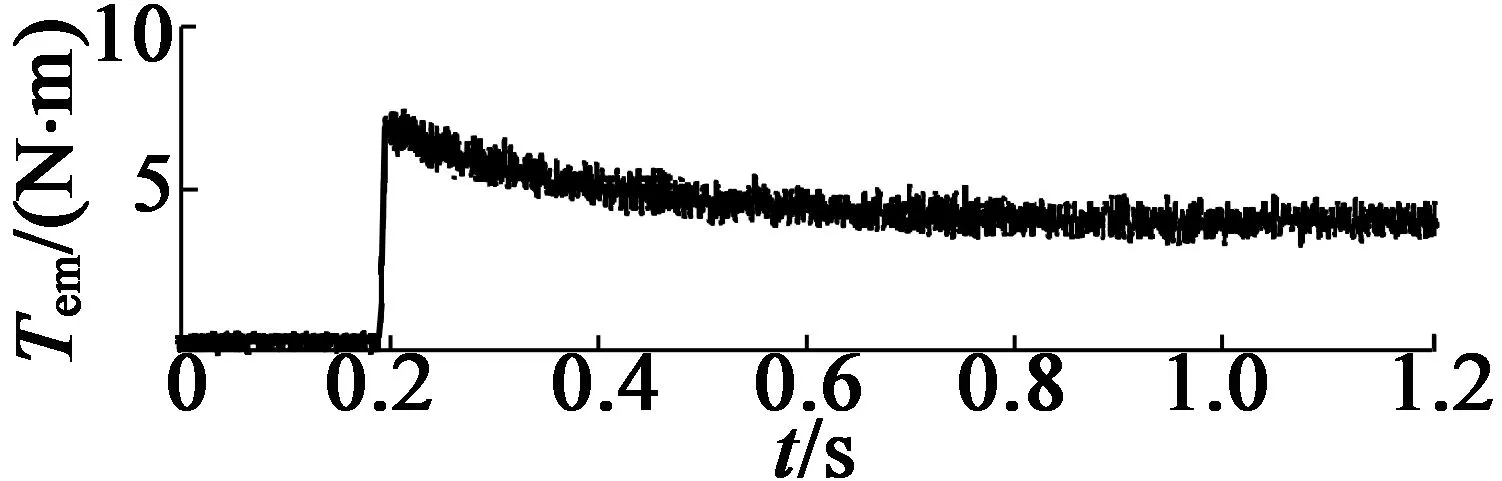
图9为电机突加负载的试验波形，如图10所示为电机的转矩阶跃控制时的试验波形。从图9中可以看到，施加到电机的负载转矩等于80%的额定转矩，因此试验验证了在新型控制作用下，电机动态响应较快，且能保持系统稳定运行。从图10可以看出,控制器的转矩跟踪响应较快，在2 ms内即可达到转矩参考值，体现了算法的优势。

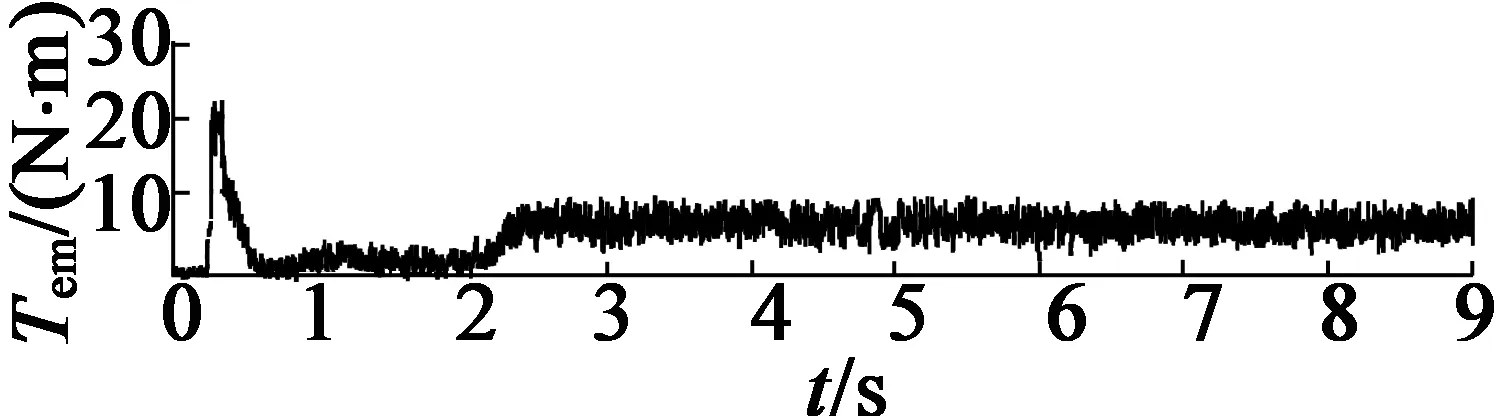
(a) 电磁转矩波形

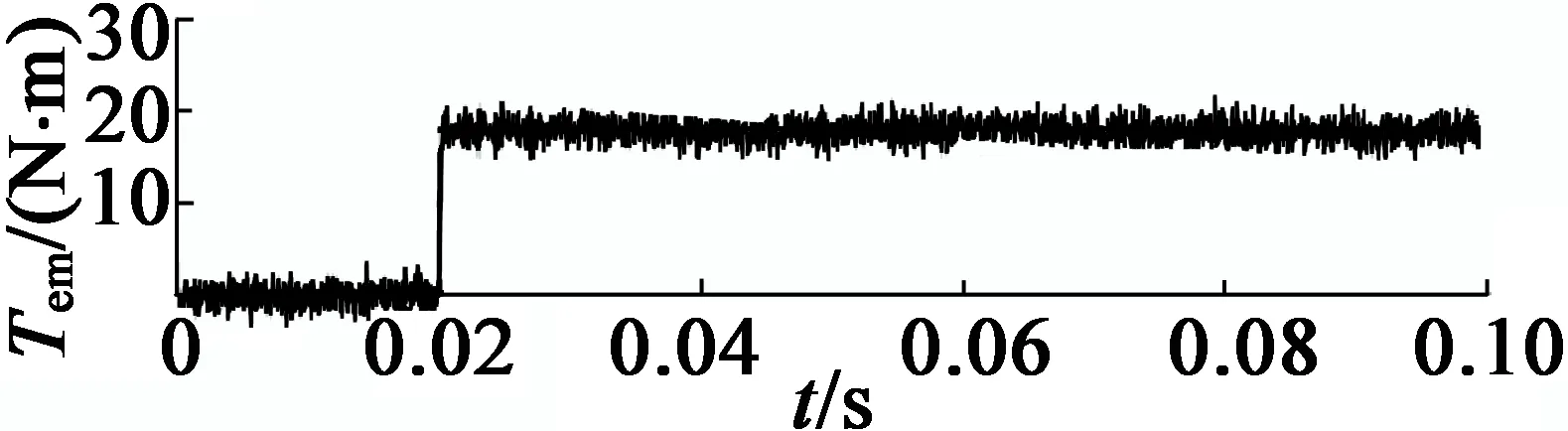
(a) 电磁转矩波形

(b) 定子电流波形

4 结 语

本文设计了一种基于有限控制集的感应电机直接相角预测控制策略，它属于计算密集型的智能控制方法，对其进行理论和试验研究后可总结:

(1)新型控制策略不直接对磁链进行控制，而是控制转矩以及定子电流和转子磁链之间的相角，将相角控制在45°后将最大限度地降低电流幅值并自动优化磁链。由于代价函数最小化计算是基于有限状态集进行的，故只需要一般性能的数字芯片即可实现，成本较低，易于工程实现。

(2)算法使用了闭环预测模型，提高了控制器的精度和鲁棒性，最后通过感应电机控制试验验证了新型控制算法的动静态性能。

[1] 周志刚．一种感应电机的解耦控制方法[J]．中国电机工程学报，2003，23(2)：121-125．

[2] 肖海峰，贺昱耀，李凯．直接转矩变结构控制的无速度传感器交流感应电机系统[J]．微特电机，2014，42(1)：63-65．

[3] 贾立辉，郑申白，张荣华．模糊PID控制的异步电机矢量调速系统仿真[J]．微特电机，2008，36(7)：47-49．

[4] 史婷娜，肖竹欣，肖有文，等．基于改进型滑模观测器的无刷直流电机无位置传感器控制[J]．中国电机工程学报，2015，35(8)：2043-2051．

[5] 梅从立，黄文涛，殷开婷，等．基于Hammerstein模型的感应电机变频器调速系统神经网络控制[J]．控制与决策，2015，30(6)：1148-1152．

[6] 齐昕，周晓敏，马祥华，等．感应电机预测控制改进算法[J]．电机与控制学报，2013，17(3)：62-69．

[7] 金辛海，张扬，杨明，等．一种感应电机预测控制的电流静差消除方法[J]．电机与控制学报，2015，19(11)：1-9．

[8] 张永昌，杨海涛．感应电机模型预测磁链控制[J]．中国电机工程学报，2015，35(3)：719-726．

[9] 刘威，甘雪，于贵，等．基于矢量控制的异步电机改进模型预测控制[J]．微特电机，2016，44(7)：66-71．

[10] 刘吉宏，徐大平，吕跃刚．双馈感应发电机转速的非线性模型预测控制[J]．电网技术，2011，35(4)：159-163．

[11] 张兴华，孙振兴，沈捷．计及逆变器电压输出限制的感应电机无差拍直接转矩控制[J]．中国电机工程学报，2012，32(21)：79-85．

[12] CORREA P,PACAS M,RODRIGUEZ J.Predictive torque control for inverter-fed induction iachines[J].IEEE Transactions on Industry Electronics,2007,54(2): 1073-1079.

[13] 张建桃，张铁民，梁莉．超声电机非线性建模和广义预测控制[J]．电机与控制学报，2011，15(6)：50-56．

[14] 刘旭东，李珂，孙静，等．基于广义预测控制和扩展状态观测器的永磁同步电机控制[J]．控制理论与应用，2015，32(12)：1613-1619．

[15] 沈坤，章兢，王坚．一种多步预测的变流器有限控制集模型预测控制算法[J]．中国电机工程学报，2012，32(33)：37-44．

[16] 杨苹，袁昊哲，许志荣，等．基于有限控制集模型预测的逆变器控制算法[J]．可再生能源，2015，33(4)：504-510．

[17] 李宁，李颖晖，韩建定，等．基于混合逻辑动态模型的三相逆变电路有限控制集模型预测控制策略[J]．电网技术，2014，38(2)：375-380．

[18] 朱晓雨，王丹，彭周华，等．三相电压型逆变器的延时补偿模型预测控制[J]．电机与控制应用，2015，42(9)：1-7．

[19] PREINDL M,BOLOGNANI S.Model Predictive Direct Speed Control with Finite Control Set of PMSM Drive Systems[J].IEEE Transactions on Power Electronics,2013,28(2):1007-1016.

[20] PREINDL M,BOLOGNANI S.Model predictive direct torque control with finite control set for PMSM drive systems,Part2:Field Weakening Operation[J].IEEE Transactions on Industry Information,2013,9(2):648-657.

[21] LASCU C,ANDREESCUDD G.Sliding-mode observer and improved integrator with DC-offset compensation for flux estimation in sensorless controlled induction motors[J].IEEE Transactions on Industry Electronics,2006,53(3):785-794.

[22] HABIBULLAH M,LU D C.A speed-sensorless FS-PTC of induction motors using extended kalman filters[J].IEEE Transactions on Industry Electronics,2015,62(11):6765-6778.