龙门式工业机器人两永磁伺服电机同步控制

董 令，李 岩，杨宏韬，刘克平

(长春工业大学,长春 130012)

0 引 言

近年来,龙门式工业机器人双电机耦合同步控制越来越多地应用在工业、农业和交通运输等行业中。由于2个永磁伺服电机之间存在速度、位置等约束，传统的PID计算繁琐求解困难，因此需要设计适当的控制器对各电机的转速进行协调控制。自从1980年Koren提出交叉耦合控制器以来[1]，又有许多研究人员将鲁棒控制[2]、滑模变结构[3]、神经网络[4]与模糊控制[5]等现代控制方法应用到多电机协调控制中，采用速度和转角(位置)双重同步多电机协调控制，取得了很好的效果。

区间矩阵方法是研究线性时变系统稳定性的重要方法之一[6]。由于双电机系统是一个多变量、强耦合、非线性时变系统，研究一种简单的提高同步性能的控制方法，保证电机在负载发生变化时仍能保持良好的同步控制性能。

本文基于区间矩阵理论将电机不确定参数进行最大值最小值估计，然后进行状态矩阵分解，并构造正定矩阵。考虑到双电机的动态性能及交叉耦合特性，将双电机的电流、速度和位置误差信号加入耦合双电机同步控制系统控制器中。设计负载转矩观测器辨识负载变化，依据负载变化调节变负载对转速的影响，根据李雅普诺夫稳定性定理验证了双电机同步系统的稳定性。

1 双电机同步数学模型建立

1.1 坐标变换

建立永磁伺服电机控制系统数学模型的坐标系通常分为2大类，一类是静止坐标系，包括三相A-B-C坐标系和α-β坐标系；另一类是旋转坐标系，常用的是两相d-q坐标系。d-q坐标系与A-B-C坐标系变换关系：

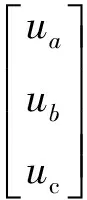
(1)

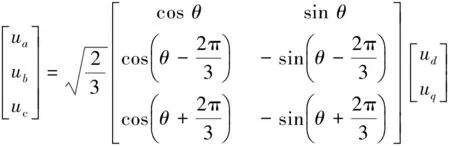
(2)

利用坐标变换关系式(1)和式(2)以及永磁同步电动机(以下简称PMSM)在A-B-C坐标系中的数学模型[7]，可以得到PMSM在d-q旋转坐标系中的数学模型：

(3)

式中:Lsd和Lsq分别表示d轴和q轴的电感;Rs是定子电阻;ψr是永磁电机的磁链;p是极对数;B是摩擦系数;J是惯性力矩;id,iq分别是d,q轴定子电流;ω是转子速度;ud,uq分别是d,q轴的电压;Tl是负载转矩。

1.2 双电机同步模型建立

龙门式工业机器人两永磁伺服电机系统可以用如图1所示的两耦合伺服电机同步控制原理图来描述[8]。该系统可分为控制器、驱动器和观测器等几部分，给定同步控制角速度ω*，控制器输出ud1,uq1和ud2,uq2分别经过驱动器作用于永磁伺服电机PMSM1和PMSM2。两电机实时的角速度反馈给控制器，同步控制系统是非线性耦合的，当负载发生变化时，角速度ω1和ω2以及各轴电流值都将发生变

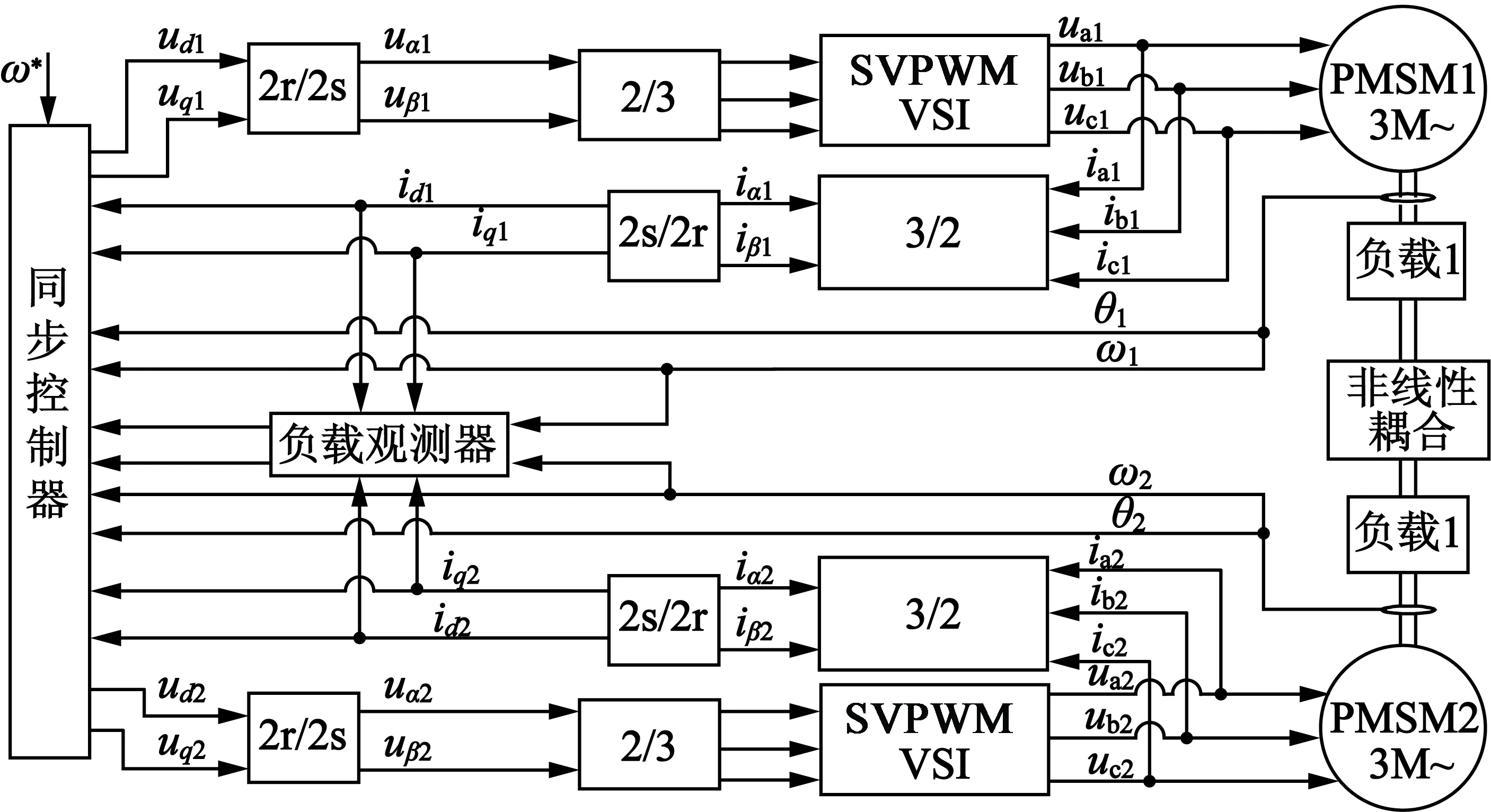
图1 两耦合伺服电机同步控制原理图

化，通过负载观测器辨识得到2个负载的变化，并反馈给控制器，控制器调整ud1,uq1和ud2,uq2各值，从而完成双电机非线性耦合同步控制。

如果转子角位置相同，这种同步是理想状态，此时两电机的耦合力是不存在的。当2个电机中的负载发生变化，这时控制2个电机速度同步是比较困难的，相互之间的影响可能会导致系统的不稳定，所以设计同步控制器是必要的。为了得到较好的控制效果，永磁伺服电机的动态模型和双电机之间的耦合关系有必要考虑。作用在转子和定子上的耦合力直接影响同步速度，2个电机的耦合是多变量非线性的，根据单个电机的模型可以得出双电机模型的表达式[8-9]：

(4)

式中:Lsdi和Lsqi分别表示d轴和q轴的电机i的电感;Rsi是电机i的电阻;ψri是电机i的磁链;p1i是电机i的极对数;Βi是电机i的摩擦系数;Ji是电机i的惯性力矩;idi和iqi分别是d,q轴电机i的定子电流;ωi是电机i的转子速度;θi是电机i的转子角速度;udi和uqi分别是d轴和q轴电机i的电压;Tli是电机i的负载转矩;f1(θ1-θ2)和f2(θ1-θ2)分别是作用在电机1和电机2上的耦合力，而且是非线性的。

实际应用中，通常作如下假设：

(5)

2 2台耦合伺服电机同步控制器设计

为了保持2台耦合伺服电机的同步运行，需要设计一个同步控制器，令：

(6)

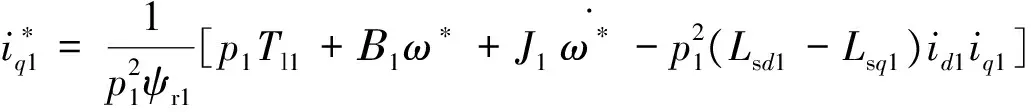
(7)

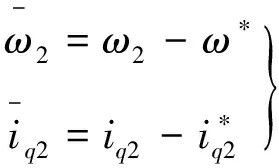
(8)

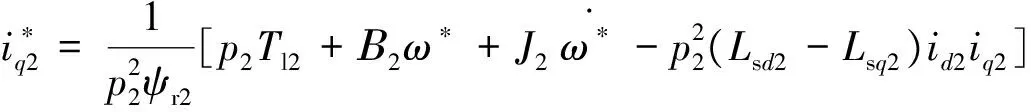
(9)

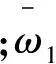
(10)

式中:uffd1,uffd2分别是电机1和电机2的d轴正反馈信号;uffq1,uffq2分别是电机1和电机2的q轴正反馈信号;ufbd1,ufbd2分别是电机1和电机2的d轴负反馈信号;ufbq1,ufbq2分别是电机1和电机2的q轴负反馈信号。令 :

(11)

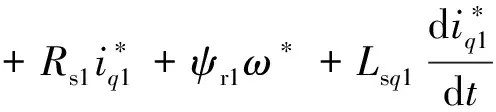
(12)

(13)

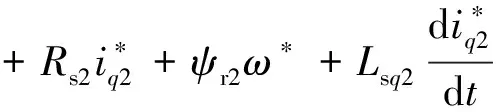
(14)

令:

(15)

ufb=[ui]4×1=[ufbd1ufbq1ufbd2ufbq2]T

(16)

uff=[uffd1uffq1uffd2uffq2]T

(17)

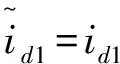
控制输入：

U=Uff+Ufb=[ud1uq1ud2uq2]T

(18)

根据以上公式，可以表述成状态方程的形式：

(19)

(20)

(21)

(22)

根据实际工程实验,有如下不等式成立：

(23)

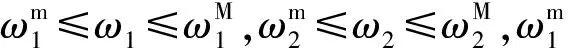
Δ*={Δ∈Rn2×n2|Δ=diag{χ11…χ1n…χn1χnnn}},(|χij|≤1,i,j=1,…,n)。

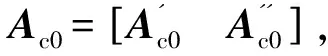
(24)

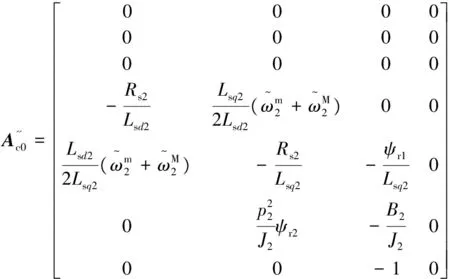
(25)

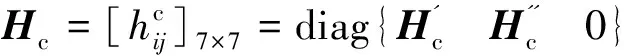
(26)

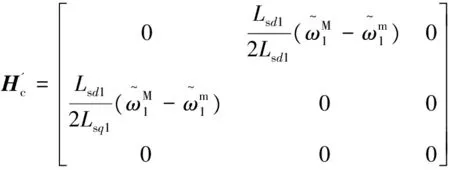
(27)

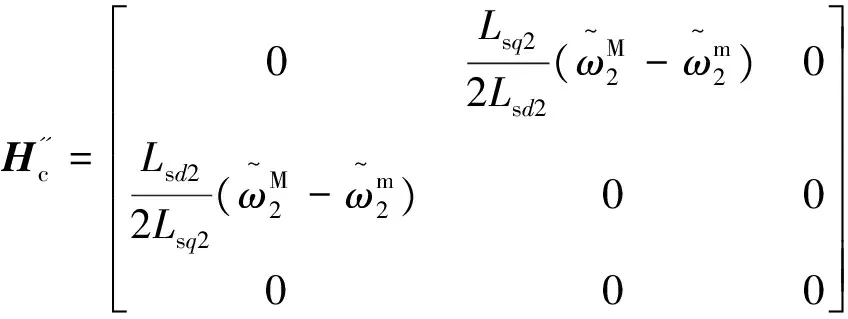
(28)

(29)

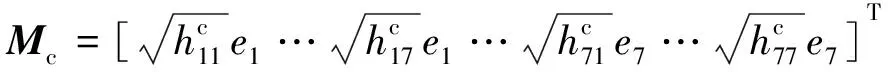
(30)

(31)

式中：α=ATc0Pc1+Pc1Ac0+KTcBTPc1+Pc1BKc+εMTcMc+L。

控制输入U=Uff+KcXc，则有Ufb=Kcc，状态方程式(19)可以写成下式：

(32)

选择李雅普诺夫函数：

Vc1=XTcPc1Xc

(33)

c(ATc0Pc1+Pc1Ac0+KTcBTPc1+Pc1BKc+

AXTcPc1GcAf1(θ1-θ2)

(34)

让：

Zc=[XTcfT1(θ1-θ2)]T

(35)

根据式(23)，式(34)可以写成如下不等式：

(36)

(37)

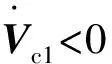
(1)s(x)<0；

根据等价不等式(3)，可得Qc1<0,可以写成式(31)。根据李雅普诺夫函数，可知系统是稳定的。

3 负载转矩观测器模型建立

控制系统式(32)稳定的前提是电机1和电机2的负载转矩是已知的，但是实际电机运行时，电机的负载转矩是未知的，所以，需要设计负载转矩观测器。通常情况下负载转矩是常数或者变化速度很慢，因此有下式：

(38)

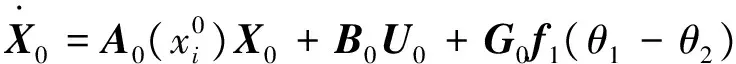
(39)

Y=C0X0

(40)

式中:

Y=[id1iq1ω1id2iq2ω2]T

负载转矩可以被表示：

(41)

( (42)

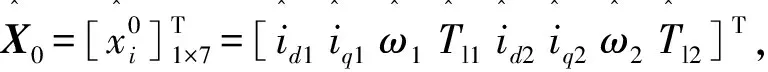
Ufb=KcXc=[ui]4×1

Kc=[kij]4×7

ki7(θ1-θ2)

ufbd1=χ11+χ12

ufbd2=χ31+χ32

ufbq2=χ41+χ42

其中:

χ11和χ21是电机1的自反馈，χ32和χ42是电机2的自反馈，χ12,χ22,χ31和χ41是双电机交叉耦合信号。从表达式可以看出，交叉耦合信号包括电流信号、速度误差信号和位置误差信号。如果增强交叉反馈信号，那么同步性能和动态性能将会得到提高。把ufbd1表达式做如下处理：

改写为：

k17(θ1-θ2)

4 实验研究及结果分析

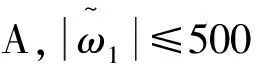
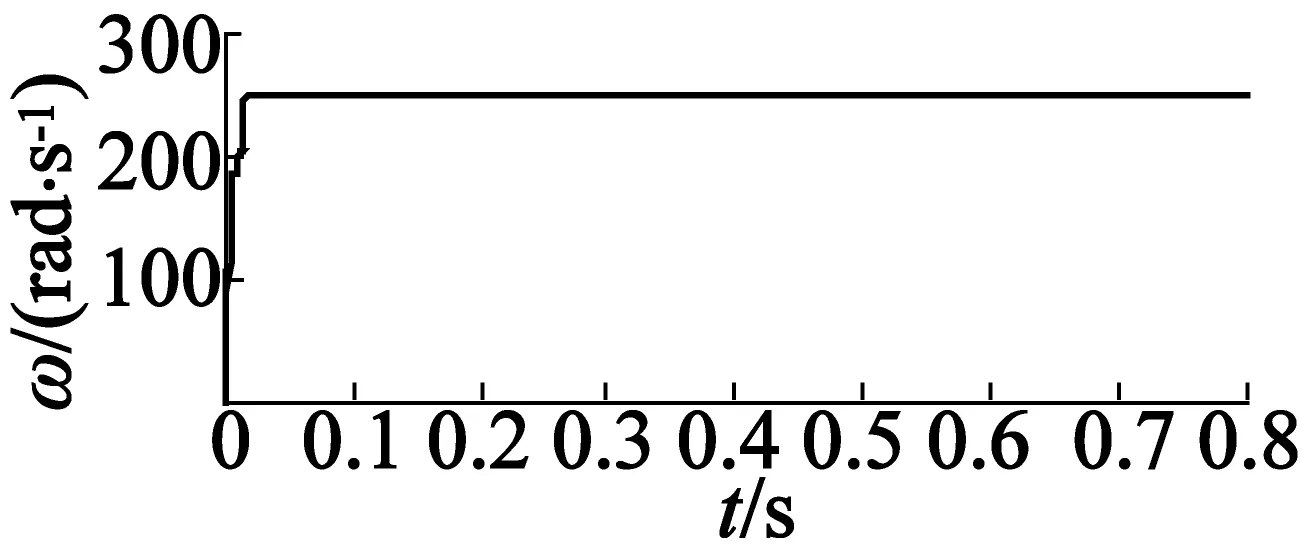
图2 电机1转速变化曲线

图3 电机2转速变化曲线

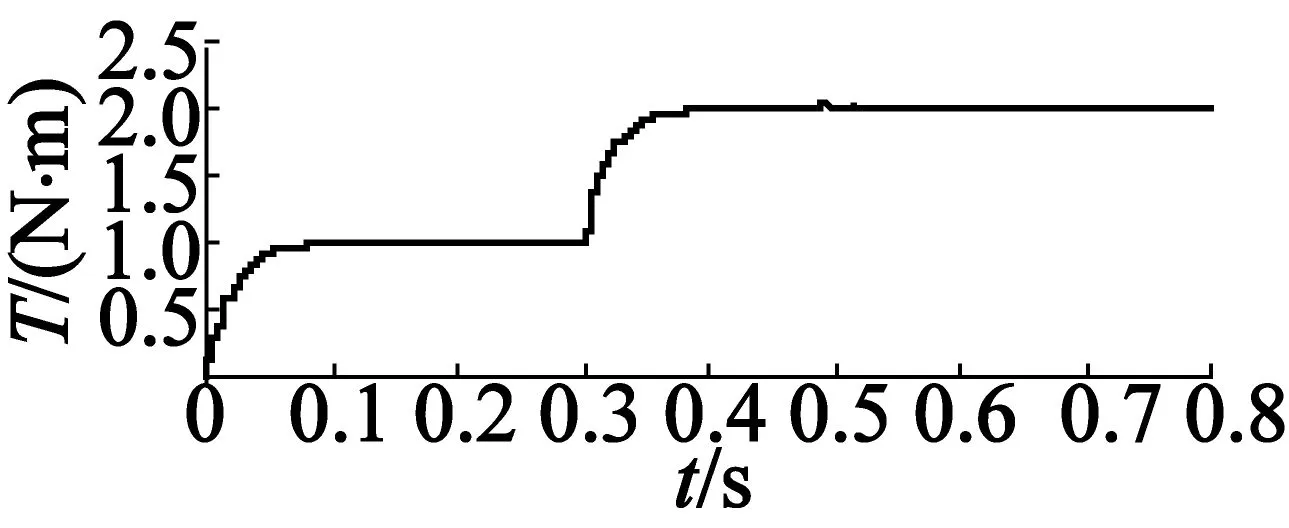
图4 电机1转矩变化曲线

图5 电机2转矩变化曲线

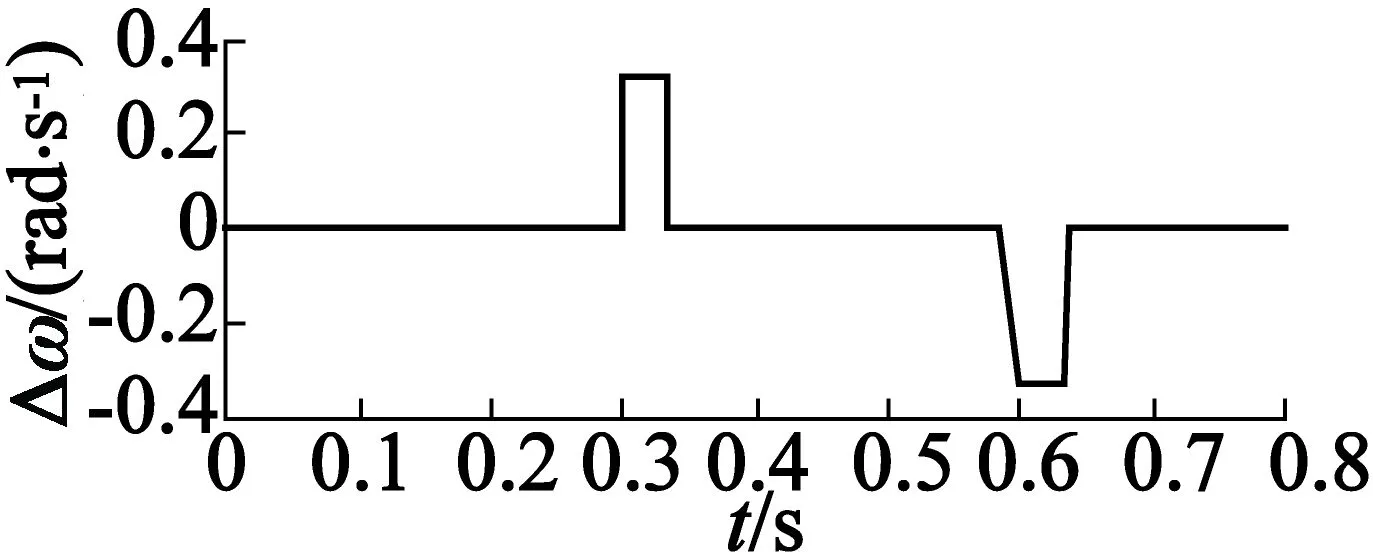
图6 双电机同步速度差变化曲线

为了验证本文提出的龙门式工业机器人控制器的同步精度，本文基于KUKA龙门式工业机器人平台进行了实际实验研究。两永磁伺服电机的给定转速为250 r/min，带动负载300 kg物体同步转动，通过在线监控得到实验结果，如图7、图8所示。从图中可以看出，控制器实时调整两电机编码器的输出值，保持两电机同步状态。为得到同步系统的控制精度，在检测画面上选取任意2个时刻t1和t2，采集2组编码器输出值和2组转速值进行分析，可以得到表1和表2。可以看出，误差在0.3 r/min左右。

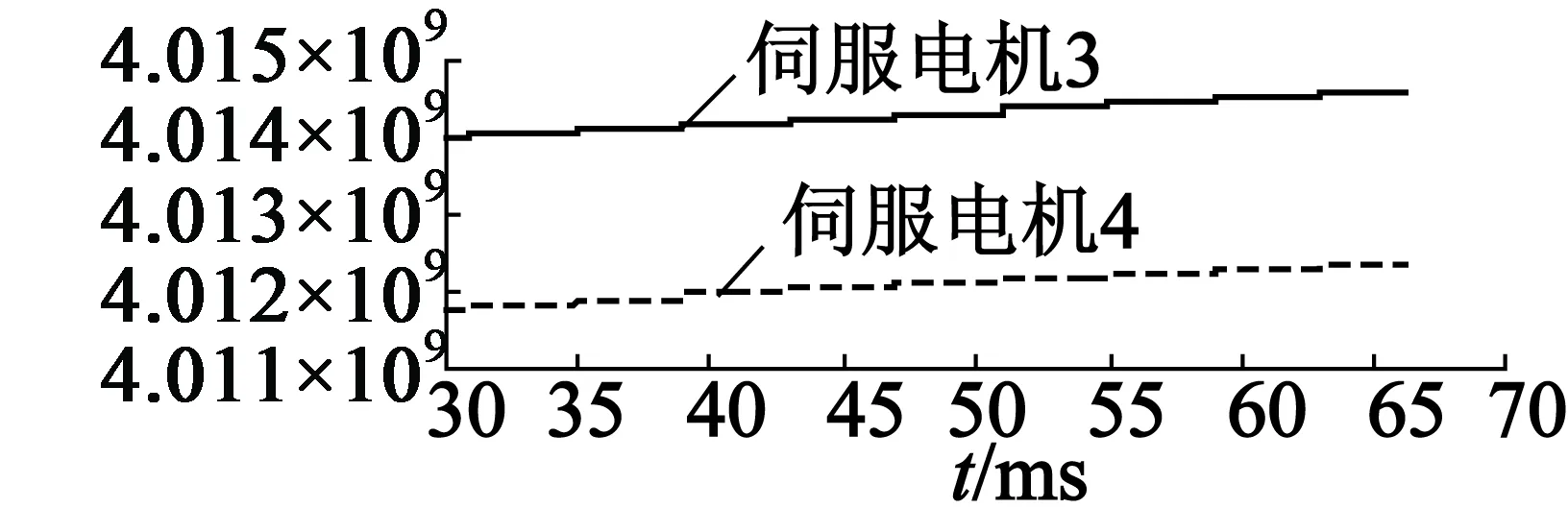
图7 编码器位置输出值变化曲线

图8 同步转速变化曲线

编码器Y(t1)Y(t2)SERVO-03401417300401438300SERVO-04401417100401438000ΔY200300

表2 t1和t2时刻双电机同步转速

5 结 语

为了解决龙门式工业机器人多变量、非线性、强耦合双电机的复杂同步控制问题，本文提出了基于区间矩阵及李雅普诺夫稳定性理论的双电机同步控制方法。首先，为得到良好的监测效果，设计了负载转矩观测器，将负载力矩值反馈至控制器，调节编码器的输出。实验结果显示，负载转矩观测器可以有效地辨识负载力矩，反映负载力矩的变化情况。其次，采用PID积分的思想，增强耦合作用强度，进而调节同步转速值。最后，通过仿真实验验证了控制器的合理性和有效性，基于实验室龙门式工业机器人控制平台进行实验验证，得到良好的控制效果，提高了双电机控制系统的同步性能。

[1] 卢金铎,刘锦波.双电机传动机械系统的同步控制[J].科技创新导报，2014,12(19)：398-400.

[2] 苏春华,刘思峰,葛世龙.具有分布时滞的随机区间系统的鲁棒镇定[J].系统工程与电子技术，2009,31(10)：2464-2468.

[3] WANG Junxiao,LI Shihua,YANG Jun.Intergral terminal sliding mode control for permanent magnet synchronous motor position servo system[C]//32nd Chinese Control Conference,IEEE,2013:4408-4412.

[4] 沈翠凤,顾光旭.复杂交流多电机系统的研究[J].微特电机，2012,40(8)：34-36

[5] FEBIN D J L,SUBBIAH V.A novel fuzzy logic based robust speed controller for permanent magnet synchronous motor servo drive[C]//2009 Region 10 Conference,IEEE,2009:1-4.

[6] 冯平，王尔智，朱伟,等.一种新的线性时变系统区间稳定性判别方法[J].辽宁石油大学学报，2004,24(2):49-51.

[7] 阮毅,陈伯时.电力拖动自动控制系统-运动控制系统[M].北京：机械工业出版社,2003.

[8] 李玉霞,赵万华,程瑶等.动梁式龙门机床的双驱同步控制系统建模[J].西安交通大学学报，2012,46(4)：119-124.

[9] 程瑶,梁滔,赵万华.动梁式龙门机床双轴同步系统的模型建立及不同步误差分析[J].机械工程学报,2013,49(13)：174-182.

[10] DENG Zhenhua,NIAN Xiaohong.Synchronization controller design of two coupling permanent magnet synchronous motors system with nonlinear constraints[J].ISA Transactions,2015(59):243-255.

[11] 廖晓昕,罗琦,梅正杨,等.关于区间矩阵稳定性、可控性、客观性的充要条件的注记[J].自动化学报,1998,24(6)：829-833.

[12] 刘巍.区间矩阵稳定性分析及在电机控制中的应用[J].控制理论与控制工程，2007.

[13] 郑大钟.线性系统理论[M].2版.北京：清华大学出版社，2013.

[14] 胡寿松,王源.区间矩阵系统的保低成本鲁棒容错控制[J].东南大学学报，2003,33(2)：186-189.