双层分段内嵌式永磁同步电动机的电磁转矩优化
上官璇峰,孙泽亚,王 秋,杨 帅
(1.河南理工大学,焦作 454000;2.国网新疆电力公司昌吉供电公司,新疆 昌吉 831100)
0 引 言
永磁同步电动机以其结构简单、功率密度大、效率高等优点,广泛应用于航空航天、风力发电、电动汽车等领域。然而永磁电机也受到转矩波动以及由其产生的噪声,运行不平稳等问题的困扰。为了解决这些问题,很多学者在抑制永磁电机转矩波动方面做了很多的分析和研究,其中有利用定子斜槽或转子斜极[1]的,有改变隔磁槽形状尺寸的[2-3],也有采用优化永磁体的极弧系数[4]的。其中斜极或斜槽设计增加电机加工难度的同时,也使绕组线圈漏感增加从而降低了平均转矩;而且文献[1-4]的优化过程使用解析法与有限元仿真相结合,计算分析过程较为复杂。文献[5-9]采用田口方法、响应曲面法、遗传算法等优化算法优化电机转矩,通过改变电机的结构尺寸来优化电机性能,这种方法避免了电机结构的复杂化,减少了复杂的计算,较为简便有效。但应用此类方法对双层分段内嵌式永磁电机进行优化的文章相对较少。本文选取了4个可能对电机转矩和转矩波动有关的影响因子,将田口方法、响应曲面法和遗传算法结合起来优化双层分段内嵌式永磁电机的转矩和转矩波动。仿真结果验证了该方法的正确性。
1 基于田口方法的电机结构参数优化
双层分段内嵌式永磁电机(3相8极)转子一极截面如图1所示。本文选取两层永磁体的极弧系数αp1,αp2, 永磁体埋入深度h和永磁体与永磁体槽长度之比l1/l24个参数为初选变量。初选变量数值如表1所示。若使用传统方法,对于4变量3水平的实验设计,需要有34种结果;若直接使用响应曲面法,并采用响应曲面法全因子设计方案,则需针对不同的变量组合设计25组样本进行分析,建模仿真耗费大量时间。现先采用田口方法对优化过程做简化处理。
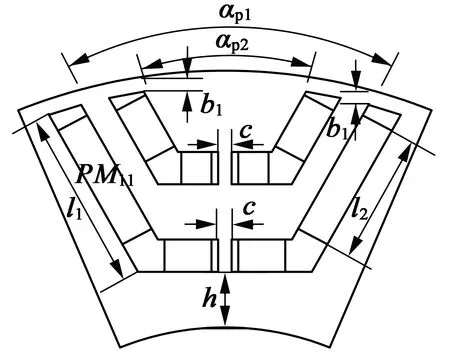
图1 多层分段内嵌式永磁电机转子一极截面图
田口方法是以概率论和数理统计作为理论基础,通过正交表来挑选试验参数和安排试验的方法。主要优点是能以较少的试验数量和实验数据得出较为理想的参数组合设计。以4变量3水平田口方法的正交表L9(34)建立实验组,只需进行9次试验,便可分析出不同参数变量改时电机性能指标的变化趋势。转子参数变量及影响因子取值如表2所示,由表2建立的试验矩阵及其转矩、转矩波动求解结果如表3所示。

表1 转子优化参数初值
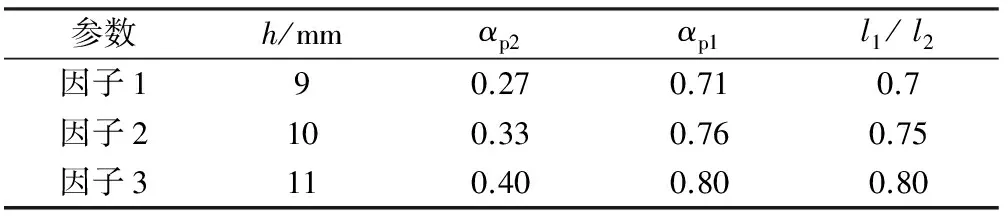
表2 转子优化参数及其影响因子取值
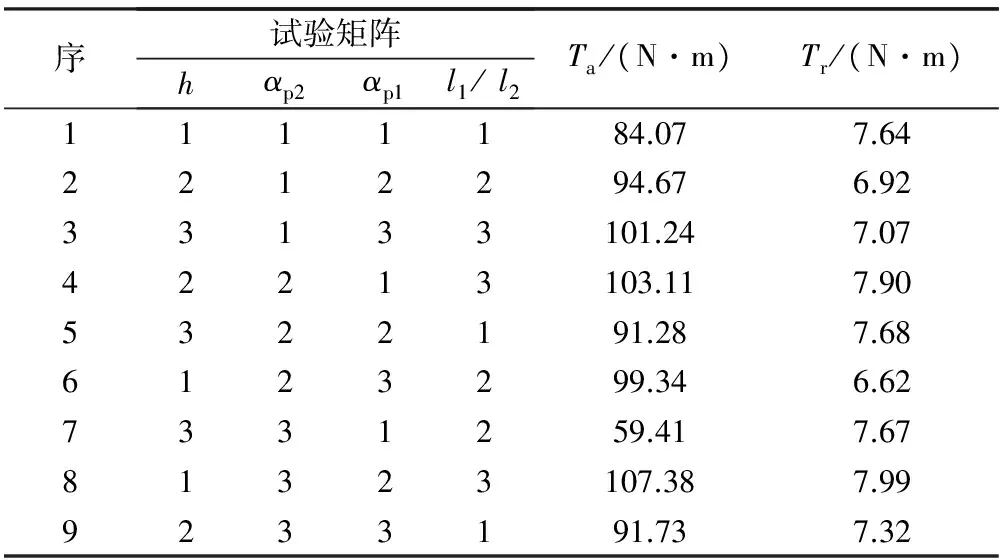
表3 试验矩阵及其有限元分析结果
由式(1)计算转矩、转矩波动的平均值,T=92.47,Tr=7.42。
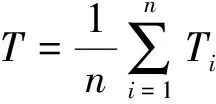
(1)
i为表3中的序,n=9。然后计算出每个参数变量在影响因子i作用下对应转矩或转矩波动的平均值。如式(2)为计算αp2在影响因子2作用下产生的转矩平均值:

(2)
式中:Ta(4),Ta(5),Ta(6)分别为表3中试验序号为4,5,6的Ta值。计算结果如表4所示。

表4 各个性能指标平均值
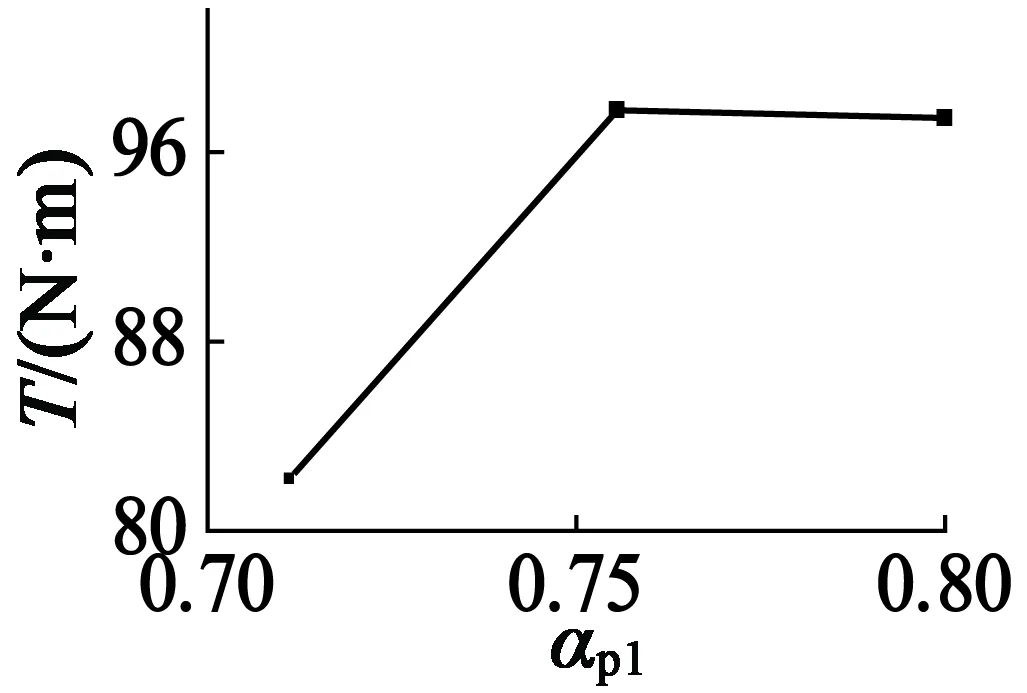
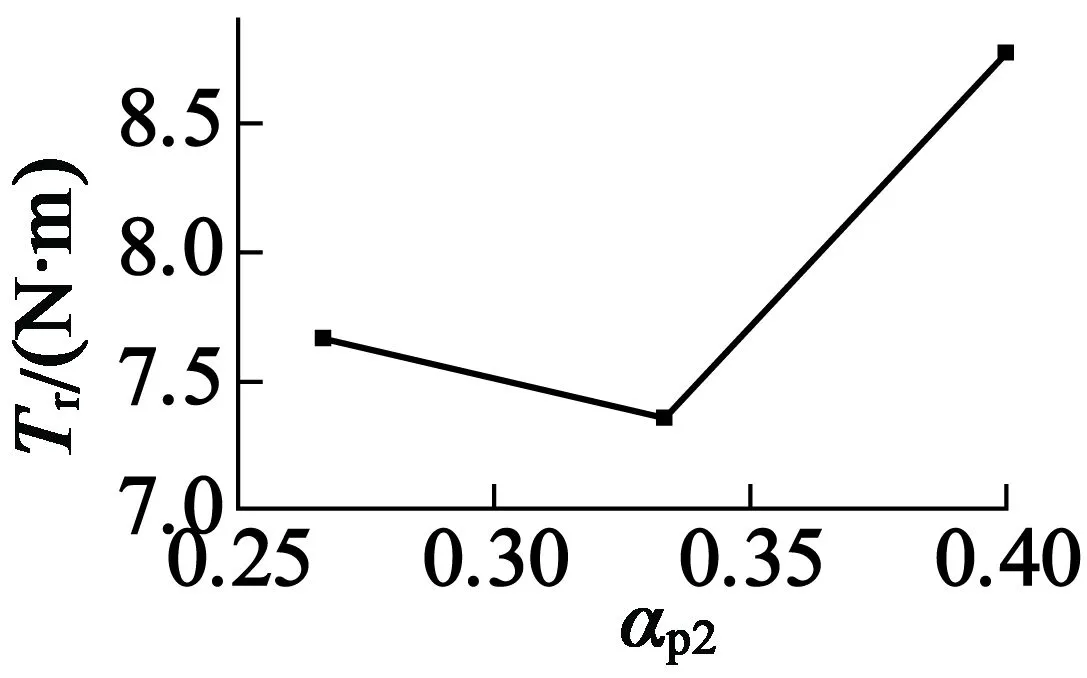
将表4中数据稍作整理即可得出各参数对电机最大转矩和转矩波动幅值的影响如图2、图3所示。由表4和图2、图3可知,随着l1/l2的增大,转矩Ta逐渐增大而转矩波动Tr逐渐减小,显然l1/l2的取值应取在该参数的取值范围上限0.8;αp2取值0.33时,电机转矩最大而转矩波动最小。对于αp1和h来说,不能从图中明显看出两参数取何值能同时满足转矩最大化和转矩波动最小化2个要求。
(a)αp1

(b)αp2

(c)l1/l2

(d)h
图2各参数对电机最大转矩的影响

(a)αp1
(b)αp2

(c)l1/l2

(d)h
图3各参数对电机转矩波动幅值的影响
电机的转矩波动Tr是一个相对值,不能单纯以转矩波动绝对值最小来进行优化,使用转矩波动百分比σ=Ta/Tr更加合适。
对于αp1和h以及σ,本文采用响应曲面法与遗传算法结合对其进行优化。
2 基于响应曲面法与遗传算法的电机结构参数优化
2.1 转矩和转矩波动响应面方程的确定
响应曲面法[10]最早由Box和Wilson提出,是一种结合了数学方法和统计分析,用来提高、改进和优化未知系统及过程的工具。
对于永磁电机来说,极弧系数αp1的改变使得相邻永磁体边端磁通密度函数畸变程度不同,永磁体埋入深度h的改变会很大程度上引起电机主磁路磁阻的改变,从而使气隙磁通密度函数产生相应变化,电机转矩也将受到影响;同时αp1,h的改变对电机电枢反应的影响也很大。较为复杂的转子拓扑结构,转子铁心各部分饱和程度的差别使得应用解析法求解响应与自变量之间关系十分困难且精度很难达到要求。本文采用响应曲面法和有限元分析相结合求解参数变量与转矩和转矩波动之间的关系。
为了保证响应面的预测精度,本文采用式(3)的二阶函数来近似建立数学模型:
式中:β为回归系数;ε为拟合误差;y为系统的响应。
有很多方法用来拟合二次响应曲面[10],中心复合表面设计(CCF)以其实验设置与操作简单,因子水平相比中心复合设计(CCD)较少,且所有试验点都不超过立方体边界的特性在实际中被广泛应用。出于理论分析的考虑[10],我们首先将原始的自变量数值进行一线性变换(代码转换),将自变量的高,低水平和中心点分别用1,-1,0来表示。则CCF的整个实验可由以下3种试验点构成:
(1)立方体点,各点坐标皆为1或-1,是实验设计中全因子实验的组成部分。如图4中C1,C2,C3,C4。
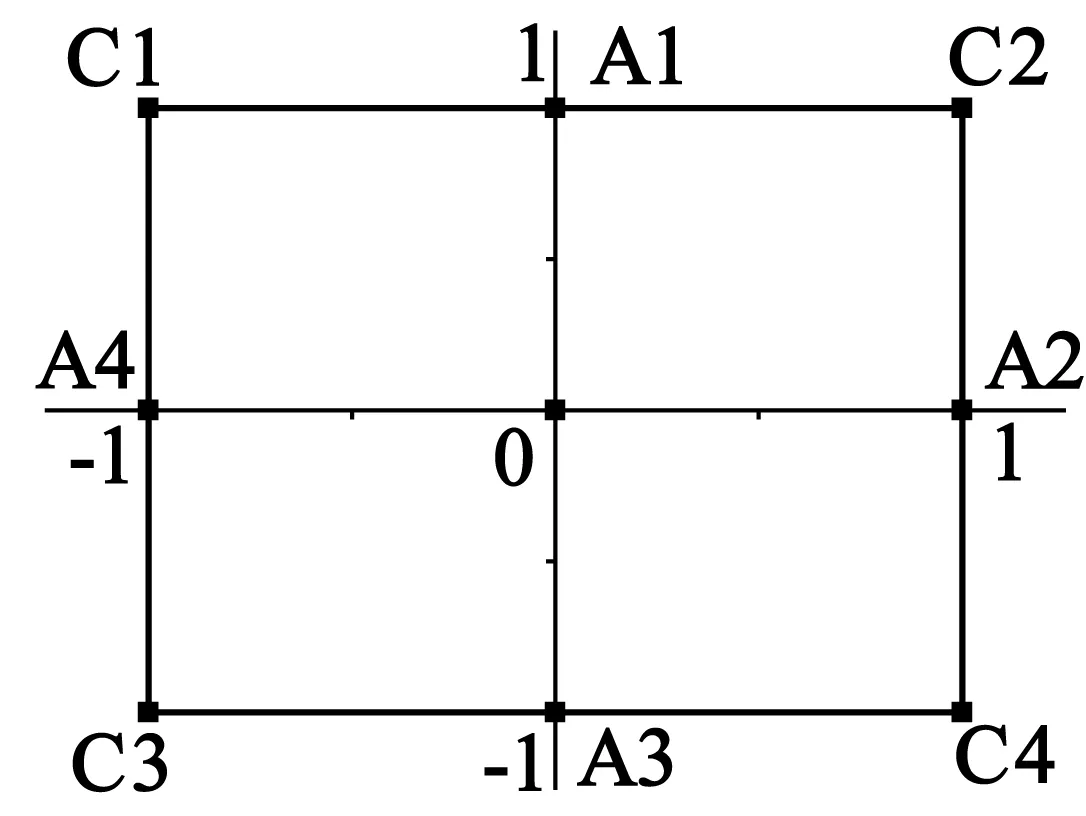
图4 二因子中心复合表面设计合成示意图
(2)轴点,一坐标为±1,另一坐标为0。如图4中A1,A2,A3,A4。
(3)中心点,坐标为(0,0)。
试验设计总试验次数由式(4)表示。
n=2k+2k+N
(4)
k为变量因子个数,本节k=2。等式右边第一项为全因子试验点数,第二项为轴点数,第三项为中心点数。
表5为图4中9个试验点的设计变量组合,由于设置中心点是为了保证整个实验区域内的预测值都有一致均匀的精度,而本实验响应结果均由有限元软件计算,预测值精度的均匀性可以保证,因此只设置了一个中心点,而在实际测量中中心点的数目应保证至少为2个点。
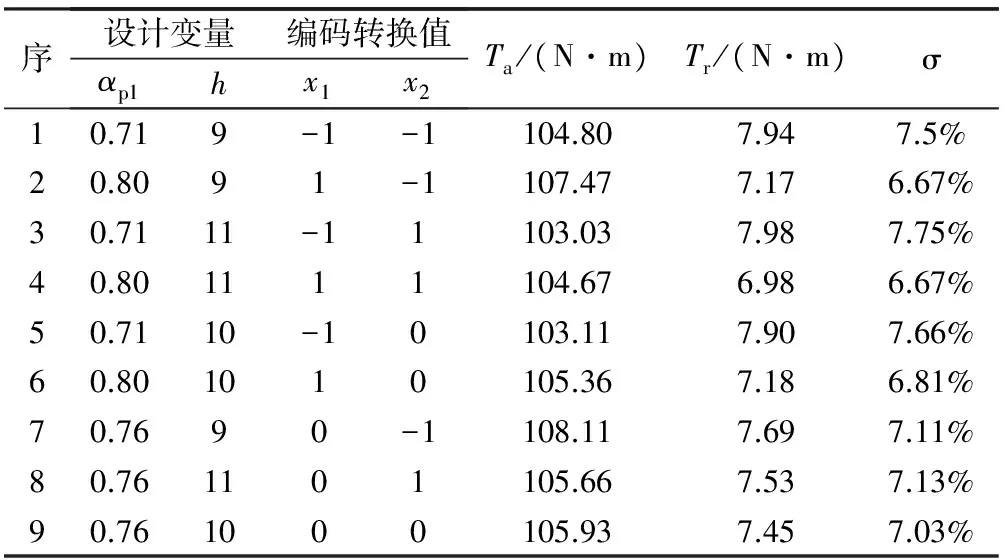
表5 CCF设计变量组合
转矩Ta和转矩波动百分比σ的响应曲面方程:
0.011 08h-0.014 06αp1·h
(6)
2.2 基于遗传算法的电机结构参数优化
本小节参照上节由响应曲面法求得的转矩和转矩波动响应面式(5)、式(6)设置适应值函数,采用遗传算法对电机的转矩Ta和转矩波动百分比σ进行全局优化,以达到增大转矩减小转矩波动的目的。
遗传算法的数学模型如下式:
(7)
式中:minF(x)是个体适应度函数,参考式(5)、式(6)给定,通过其对个体的适应度进行评价。G(xi)是种群规模控制函数,R表示个体取值范围。
优化过程中种群大小M设为100,进化终止代数T设为300,交叉概率Pc设为0.85,变异概率Pm为默认值。变量取值范围αp1取[0.71,0.82],h取[8,11]。图5为种群各代适应度函数的最佳值和平均值。求得最优解为当αp1=0.799 86,h=9.004
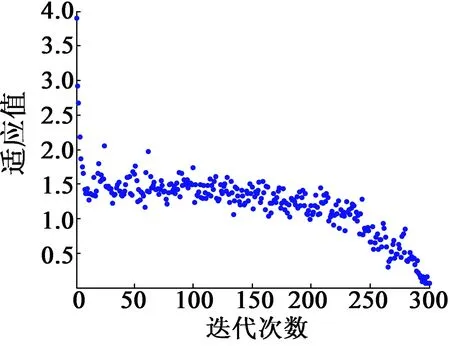
图5 各代适应度函数的最佳值和平均值
[3] GEORG K.Permanenterregte synchronmaschine.DE19851883 A[P].2000.
[4] TSURUTA T,KANEBAKO H,OTSUKI N,et al.Permanent magnet embedded motor.US,US7042127[P].2006.
[5] EVANS S A.Salient pole shoe shapes of interior permanent magnet synchronous machines[C]//XIX International Conference on Electrical Machine.IEEE,2010:1-6.
[6] FEI W,ZHU Z Q.Comparison of cogging torque reduction in permanent magnet brushless machines by conventional and herringbone skewing techniques[J].IEEE Transactions on Energy Conversion,2013,28(3):664-674.
[7] ZHU Z Q,WU L J,MOHD JAMIL M L.Influence of pole and slot number combinations on cogging torque in permanent-magnet machines with static and rotating eccentricities[J].IEEE Transactions on Industry Applications,2014,50(5):3265-3277.
[8] QIAN H,GUO H,WU Z Y,et al.Analytical solution for cogging torque in surface-mounted permanent-magnet motors with magnet imperfections and rotor eccentricity[J].IEEE Transactions on Magnetics,2014,50(8):1-15.
[9] GASPARIN L,CERNIGOJ A,MARKIC S,et al.Additional cogging torque components in permanent-magnet motors due to manufacturing imperfections[J].IEEE Transactions on Magnetics,2009,45(3):1210-1213.
[10] NAKANO M,MORITA Y,MATSUNAGA T.Reduction of cogging torque due to production tolerances of rotor by using dummy slots placed partially in axial direction[J].IEEE Transactions on Industry Applications,2015,51(6):4372-4382.
[11] COENEN I,GIET M V D,HAMEYER K.Manufacturing tolerances: estimation and prediction of cogging torque influenced by magnetization faults[J].IEEE Transactions on Magnetics,2012,48(5):1932-1936.
[12] KIM Y K,LEE J J,HONG J P,et al.Analysis of cogging torque considering tolerance of axial displacement on BLDC motor by using a stochastic simulation coupled with 3-D EMCN[J].IEEE Transactions on Magnetics,2004,40(2):1244-1247.
[13] ZHU Z Q,AZAR Z,OMBACH G.Influence of additional air gaps between stator segments on cogging torque of permanent-magnet machines having modular stators[J].IEEE Transactions on Magnetics,2012,48(6):2049-2055.
[14] DUTTA R,CHONG L,RAHMAN M F.Design and experimental verification of an 18-slot/14-pole fractional-slot concentrated winding interior permanent magnet machine[J].IEEE Transactions on Energy Conversion,2012,28(3):181-190.
[15] MIRAHKI H,MOALLEM M.Design improvement of interior permanent magnet synchronous machine for integrated starter alternator application[C]//Electric Machines & Drive Conference.IEEE,2013:382-385.

