基于等效励磁电流的同步磁阻电机磁饱和模型研究
孙鹤旭,石乐乐,董 砚,荆 锴,颜 冬
(河北工业大学,天津,300130)
0 引 言
同步磁阻电机(以下简称SynRM)其定子结构与感应电机相同,转子为凸极结构,利用磁阻转矩原理产生电磁转矩。由于转子无永磁体,具有低成本、低转矩脉动、低损耗、高转矩密度等优点,目前在机床主轴驱动、船舶等领域具有很好的应用前景[1-4]。
同步磁阻电机在实际运行中,受主磁路饱和和交叉饱和的影响,直轴电感Ld,交轴电感Lq并非定值,严重影响暂态响应和精确控制。因此,搭建考虑磁饱和的SynRM电机模型和研究磁饱和对SynRM电机参数的影响,对高品质控制具有重要的意义。文献[6]对同步磁阻电机做了大量的的实验,但是这些分析局限于理想的电机模型,其控制效果很差。文献[7]通过实际的id,iq拟合出id的优化值,对该优化值与实际值的偏差进行PI控制。在相同工况下使用该方法可以减小定子电压和电流,提高了SynRM的功率因数。文献[8]针对磁路饱和现象作了大量研究,认为Ld仅与id相关,通过曲线拟合的方法得出Ld与id的关系式,而Lq在任何工况下认为是个定值。若不考虑交叉饱和对Ld的影响,仅根据id与拟合的曲线得到Ld,会导致Ld不精确。文献[5]基于磁链搭建了考虑磁饱和的同步磁阻电机模型,并提出改进的基于磁链观测器的同步磁阻电机矢量控制算法。该模型虽然避免了对d,q轴电感的需要,但是引入了磁链观测器的误差。所提出的电压模型磁链观测器依赖于定子电阻,在实际运行中电阻值随工作环境而变化,导致磁链估算不准确,影响电机模型的准确性。
本文首先分析了磁饱和对同步磁阻电机的影响,用考虑主磁路饱和与交叉饱和的等效励磁电流搭建同步磁阻电机饱和模型。用单磁饱和参数分别表征电机受磁饱和的程度,该磁饱和参数是等效励磁电流的函数,通过曲线拟合得到磁饱和参数的表达式。该模型简单、准确,能体现电机的实际过程。
1 同步磁阻电机及其理想模型
本文所研究实验样机是自制的TLR (Transversally-laminated-rotor)转子同步磁阻电机,其定、转子截面示意图如图1所示。电机的定子结构与三相异步电动机Y160-4M的定子相同,极对数为2,定子槽36,节距为9,外径260 mm,内径170 mm。转子是由冷轧硅钢片交替叠压而成。图2为实验样机的转子加工示意图。

图1 四极实验样机定、转子截面图

图2 四极实验样机加工示意图
现有的SynRM理想模型认为气隙磁动势呈正弦规律分布;不考虑空间谐波、齿槽效应、趋肤效应;忽略频率和温度对定子电阻的影响。其中Ld,Lq为定值,在任何工况下不随电流变化。其理想数学模型:
(1)
Tem=p(Ld-Lq)idiq
(2)

2 考虑磁饱和同步磁阻电机非线性模型
同步磁阻电机在实际运行中,受磁饱和的影响d轴、q轴电感并不是定值,而随电流变化。利用Ansoft软件可得到实验样机Ld,Lq随id,iq变化的数据,可得测试曲线,如图3所示。


图3 Ld,Lq随id,iq的变化曲线
从图3中可以看出,Ld主要随id非线性变化,同时也随iq变化,Lq主要随iq非线性变化,同时也随id变化。Ld不仅受主磁路饱和的影响,同时还受交叉饱和的影响。在磁饱和情况下,磁饱和会导致Ld,Lq减小,代入电机转矩方程式(2),导致电磁转矩也减小。若Ld,Lq非定值,代入式(1)和式(2),会影响系统的暂态响应和高品质控制。因此,搭建一个准确简单的磁饱和模型很有必要。
引入等效励磁电流来考虑主磁路饱和与交叉饱和对d轴电感Ld和q轴电感Lq的影响,其等效励磁电流定义如下:

( (3)

等效励磁电流由励磁电流id和q轴电流iq共同决定,不仅考虑主磁路饱和,还考虑交叉饱和。其中主磁路饱和主要由励磁电流id引起,交叉饱和主要是iq对励磁电流id的影响。

(4)
由式(4)可知,在电机全范围运行过程中,无论电机是否受磁饱和影响,Lq/Ld为定值,即凸极系数k为定值。因此可以找到磁饱和参数Ks与等效励磁电流Im的关系,在不同电流情况下,用等效励磁电流Im来修正磁饱和参数Ks的值,利用式(4)求出在磁饱和情况下电机d,q轴的电感值。
由图3和式(4)可得实验样机磁饱和参数的变化曲线,如图4所示。利用MATLAB软件可拟合出磁饱和参数的表达式:

(5)
式(5)中参数的值在表1中给出。以实验样机为例,电机磁饱和的临界点为等效励磁电流Im=10 A,d轴电流值id=8 A。当励磁电流Im<10 A (id<8 A)时,磁饱和参数Ks(Im)=1,此时认为电机未进入磁饱和状态。当等效励磁电流Im>10 A (id>8 A),磁饱和参数Ks(Im)<1,此时认为电机进入磁饱和状态,随着等效励磁电流Im的增大,电机受磁饱和越严重,磁饱和参数Ks(Im)的值越来越小,如图4所示。

图4 实验样机d轴饱和参数变化曲线
磁饱和参数表达式中系数的值如表1所示。

表1 磁饱和参数表达式中系数取值
于是可得饱和磁链方程:
(6)

将式(6)代入式(1)可得磁饱和下同步磁阻电机的数学模型,将其改写为状态空间表达式:
(7)
磁饱和下的转矩方程:

(8)
比较式(8)和式(2)可看出,非磁饱和条件下,Ks(Im)=1,磁饱和模型的电磁转矩和理想模型的电磁转矩相同,在磁饱和条件下,Ks(Im)<1,电机的电感Ld,Lq减小,磁饱和模型的电磁转矩小于理想模型的电磁转矩,带载能力减小,只能通过增大电流提高带载能力。
3 模型仿真及实验验证
首先搭建了同步磁阻电机理想的线性模型和考虑磁饱和的非线性模型,采用感应轴恒电流控制的矢量控制对模型进行验证。其控制框图如图5所示。

图5 感应轴恒电流矢量控制框图
实验样机的具体参数如表2所示。

表2 实验样机参数表
设定运行时间为300ms,转速为1 500r/min,给定id=10A,iq的限幅值为15A,负载转矩为15N·m。图6中的(1)为理想模型的转速、d轴电流、q轴电流、定子线电流的仿真曲线,图6中的(2)为考虑磁饱和非线性模型的转速、d轴电流、q轴电流、定子线电流的仿真曲线。从图6(a)可以看出,理想模型转速响应较快,在0.08s达到额定转速,而磁饱和模型在0.18s达到额定转速,暂态过程增加了1.25倍,这是因为电机在起动过程中电流很大,进入磁饱和,严重影响转矩,导致转速响应较慢。图6(b)是d轴电流的响应曲线,理想模型和磁饱和非线性饱和模型的d轴电流最终稳定在10A。图6(c)是q轴电流的响应曲线,进入稳态后,理想模型的iq为3.65A,磁饱和非线性模型iq为6A,增大了64%。图6(d)为定子线电流波形,理想模型的定子线电流为11A,而磁饱和模型的定子线电流为12.5A,增大了13%。电机在磁饱和情况下,电感减小,导致输出转矩减小,增大电流才能带负载运行。

(a) 转速响应曲线

(b) d轴电流响应曲线

(c) q轴电流响应曲线
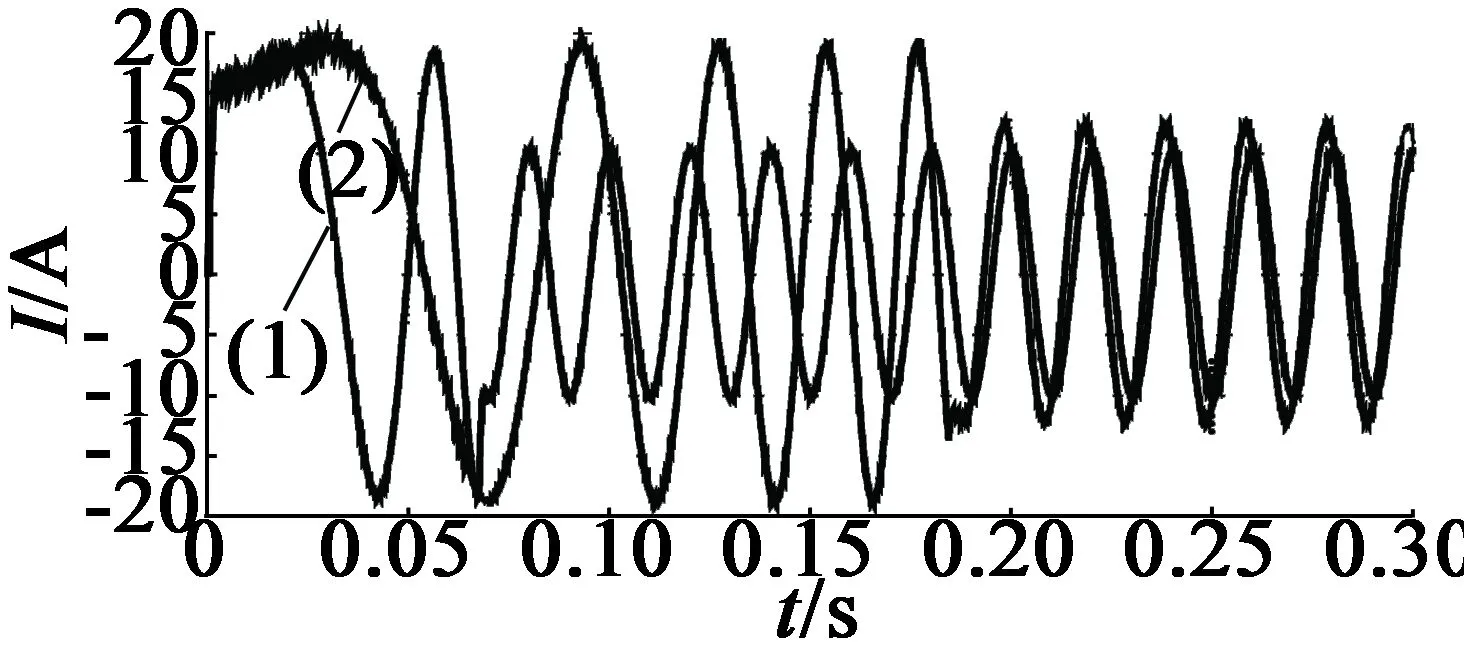
(d) 定子线电流响应曲线
另外,本文对理想模型与磁饱和模型的线电流平方和转矩的关系进行了研究。图7为线电流平方与电磁转矩的关系曲线,图7中的(1)是理想模型定子线电流平方与电磁转矩的关系曲线,图7中的(2)是磁饱和非线性模型线电流平方与电磁转矩的关系曲线,图7中的A点为饱和与非饱和的临界点,对应线电流为8A。线电流小于8A时,电机未进

图7 线电流平方与电磁转矩的关系
入磁饱和,电流幅值平方与电磁转矩呈线性,当进入磁饱和后,转矩增加缓慢,呈非线性。电流越大,磁饱和越严重,单位电流输出转矩越小。
最后搭建了感应轴恒电流矢量控制的同步磁阻电机实验平台。该控制平台主要由控制板和功率板组成。其中功率板由三相不可控整流电路、电源系统、三相电压型逆变器、电流检测电路构成。控制板以TI公司的TMS320F28335为核心芯片,其实验平台如图8所示。

图8 实验平台
实验中采用感应轴恒电流控制的矢量控制策略,d轴电流给定值为10A,使电机工作在额定转速下,记录了负载转矩为15N·m的转速、d轴电流、q轴电流、定子线电流的波形,如图9所示。实验波形由记录仪存储,然后导入MATLAB处理。从图9(a)可看出,电机起动的暂态过程为0.18s左右,与考虑磁饱和非线性模型的转速仿真波形一致。图9(b)为实验样机的d轴电流波形,选取了电机稳定后的一段波形,d轴电流稳定在10A。图9(c)为实验样机的q轴电流波形,实际值为6.1A,与考虑磁饱和非线性模型的q轴电流仿真波形一致。图9(d)为实验样机的定子线电流波形。实际的定子线电流为12.5A左右,大于理想模型的定子线电流11A,与考虑磁饱和非线性模型的定子线电流仿真波形一致。通过对比实验波形和仿真波形,磁路受电流影响较大,考虑磁饱和模型的定子电流与实验样机波形基本相同。故所搭建的考虑磁饱和非线性模型准确。

(a) 转速响应曲线

(b) d轴电流响应曲线

(c) q轴电流响应曲线

(d) 定子线电流响应曲线
4 结 语
本文针对同步磁阻电机在实际运行中磁饱和现象,首先分析了磁饱和对同步磁阻电机Ld,Lq的影响,引入等效励磁电流来考虑主磁路饱和与交叉饱和。用磁饱和参数表征电机受磁饱和的程度,该磁饱和参数是等效励磁电流的函数,通过曲线拟合得到磁饱和参数的表达式。在MATLAB/Simulink中搭建了考虑磁饱和的非线性数学模型,并搭建了SynRM控制系统硬件平台,仿真和实验验证了所提出的考虑磁饱和模型的正确性,为理论研究提供了模型参考。
[1] 王成元,夏加宽,孙宜标编著.现代电机控制技术[M].北京:机械工业出版社,2008.
[2] 夏军,黄声华,辜承林.轴向叠片各向异性转子电机及其矢量控制系统[J].中小型电机,1997(6):1-6.
[3] 吴志峤,辜承林.ALA转子电机稳定性研究[J].电机与控制学报,2003,7(3):182-186.
[4] 赵争鸣.新型同步磁阻永磁电机发展及现状[J].电工电能新技术,1998(3):22-25.
[5] 杨超,廖勇,卢权华,等.考虑磁路饱和同步磁阻电机的矢量控制[J].微电机,2013,46(11):57-61.
[6]BEZRE,LAGERQUISTR,JOVANOVICM,etal.Controlofsynchronousreluctancemachines[J].IEEETransactionsonIndustryApplications,1993, 29(6):1110-1122.
[7]MADEMLISC.Compensationofmagneticsaturationinmaximumtorquetocurrentvectorcontrolledsynchronousreluctancemotordrives[J].IEEETransactionsonEnergyConversion,2003,18(3):379-385.
[8]CAPORAL-MORALESR,PACASM.Apredictivetorquecontrolforthesynchronousreluctancemachinetakingintoaccountthemagneticcrosssaturation[J].IEEETransactionsonIndustrialElectronics,2007,54(2):1161-1167.

