基于衰减记忆卡尔曼滤波的无刷直流电机转子位置估计
詹国兵
(徐州工业职业技术学院,徐州 221140)
0 引 言
无刷直流电机(以下简称BLDCM)因其高效率、易于控制等优点被广泛使用。该电机转子为永久磁钢,定子为电枢绕组,为产生单一方向的力矩,定子永久磁钢磁场和转子电枢反应磁场必须相互垂直,要求控制系统需要明确当前转子位置。现今大部分无刷直流电机采用霍尔位置传感器,但存在成本高、尺寸大、可靠性差等问题,因此学者致力于无位置传感器的研究[1-5],如:文献[1]设计了基于粒子群优化算法的BLDCM转速PID控制系统,通过检测电机的反电动势来获得转子的位置信息,并验证了在空载和满载的情况下电机的转速、转矩响应情况。文献[5]提出了一种基于线电压的转子位置检测方法,通过获得线电压波形计算电机的反电动势,判断电机的换相点。
卡尔曼滤波作为一种最优状态估计,在转子位置信息估计中获得了广泛的应用[6-11],如:文献[6]采用扩展卡尔曼滤波的方法,通过量测电机的线电压和相电流实现电机转子位置的估计。文献[7]设计了双扩展卡尔曼滤波器(以下简称DEKF)无传感器控制方法,该方法同时对电机的状态和参数进行滤波,解决了电机参数不准确引起滤波器发散问题,但控制模型不精确依然会导致滤波器发散。文献[9]研究了基于扩展卡尔曼滤波(以下简称EKF)相位增益校正的无传感器BLDCM速度控制,针对不同转速校正了反电动的相位滞后和幅度畸变。文献[11]基于EKF并从反电动势归一化值中获取电机的转子位置信息。
BLDCM参数不易精确测量且运行时会发生变化,所建立的电机数学模型是在理论假设基础上存在误差,这导致在使用卡尔曼滤波时容易出现滤波发散、精度变差、速度变慢。衰减记忆卡尔曼滤波(以下简称MAEKF)通过弱化旧量测值权重,提高新量测值权重,虽然失去了理论上的最优,但保证了滤波器的收敛和稳定性[12-14]。本文在分析BLDCM数学模型的基础上,通过对电机的相电流进行量测,利用MAEKF实现电机的转子位置角、转速的估计,然后通过转子位置角和相电流导通关系实现电机的换相。该方法对系统的模型和参数的准确性要求较低,系统稳定性高,具有较强的鲁棒性。
1 BLDCM数学模型
无刷直流电机虽然也称为直流电机,但与直流电机有本质区别。该电机主要是由转子和定子2部分组成。其中,转子是电机旋转部分,主要由转轴、永久磁钢和磁轭等部件组成,永久磁钢在气隙中建立永磁磁场;定子主要由绕组、轴承、机盖等部分组成,工作时,绕组中通入梯形波相电流,通过换相控制,绕组在气隙中产生变化磁场。转子在一周期内产生恒定方向的力,驱动转子连续旋转。转子磁钢旋转之后,旋转的永磁磁场又反过来切割绕组线圈,并在定子绕组中产生感应电势。从BLDCM工作原理可以看出,该电机的相电流、反电动势、相电压等必定存在数学上的一一对应关系。
1.1 微分方程模型
忽略气隙不均匀性和边缘扩散现象对气隙磁感应强度的影响,BLDCM气隙磁感应强度可认为沿定子内径表面呈梯形分布。以a相绕组为例,a相绕组反电动势可表示:
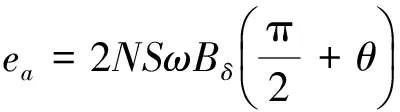
(1)
式中:N为绕组的匝数;S为绕组在定子内径表明围成的面积;ω为电机电角速度;θ为转子位置角。
BLDCM绕组相电压由电阻压降、交变电流引起的绕组自感电动势、绕组间互感电动势和绕组磁通量变化引起的感应电动势组成,a相绕组相电压可表示:
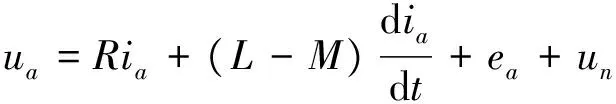
(2)
式中:R为每相绕组电阻;L为每相绕组自感;M为a相绕组与b相和c相绕组的互感;ia为a相绕组的电流;un为中性点电压。
b相,c相绕组相电压与a相类似,三相绕组的相电压可表示:

(3)
式中:ua,ub,uc为三相绕组相电压;ia,ib,ic为三相绕组电流;ea,eb,ec为三相反电动势;R为每相绕组电阻;Ls为每相绕组自感与互感差;Ls=L-M。
无刷直流电机转矩表达式可表示:
P=Teω
(4)
式中:Te为电磁转矩;ω为电机机械角速度。
电磁功率为每相反电动势与相电流的乘积之和,即:
P=eaia+ebib+ecic
(5)
代入式(5),Te可表示:
Te=(eaia+ebib+ecic)/ω
(6)
代入式(5),电磁转矩可表示:
Te=λm(Bδaia+Bδbib+Bδcic)
(7)
式中:λm=2NS;Bδa,Bδb,Bδc分别为a,b,c相绕组的气隙磁密。
电机的运动方程可表示:
(8)
式中:TL为负载转矩;J为转子转动惯量;Bv为粘滞摩擦系数。
电机的转子位置角与转速关系可表示:
(9)
1.2 无刷直流电机MAEKF状态模型
无刷直流电机MAEKF模型的状态方程可以通过式(3)、式(8)、式(9)作代数变换得到。这里选择三相电流、电机转速和转子位置角作为状态变量,得到BLDCM的MAEKF状态模型如下:
xk+1=Φkxk+Rkuk
(10)
式中:xk=[ia,ib,ic,ω,θ]T
uk=[ua,ub,uc,TL]T。
2 MAEKF无传感器控制实现
2.1 无刷直流电机MAEKF设计
无刷直流电机同其它电机一样,电机在运行时绕组电阻、电感、绕组与绕组之间的互感、磁链等参数均会因为电机运行状态的变化而发生变化,最终导致电机的数学模型产生失真。BLDCM的数学模型是在忽略涡流损耗、磁滞损耗、齿槽效应等基础上建立的,这也会导致电机模型在一定程度上的失真。因此,BLDCM无传感器控制需要对模型敏感性不高的、鲁棒性更好的滤波器。MAEKF与传统卡尔曼滤波器最大的不同之处在于引入衰减因子,降低滤波器对前期量测值的敏感程度,把重点放在最近的量测值上,降低了系统因累积误差导致的发散问题。加入衰减因子α导致卡尔曼滤波器在理论上失去了最优性,但稳定性和收敛性更好。
建立基于相电流的BLDCM状态空间方程,并离散化得:
xk+1=Φkxk+Rkuk+Gkwk
(11)
yk=Hkxk+Qkvk
(12)

参考文献[7],系统的随机扰动和量测噪声的协方差矩阵Gk和Qk:
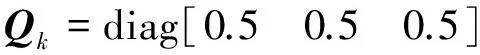
在k时刻,系统的估值方程可表示:
(13)
式中:Kk为衰减记忆卡尔曼滤波增益。该值的大小可以决定滤波器估计与真实状态之间的偏差程度,该值越大,系统的估值越接近于系统的量测值,反之越接近于系统的计算值。
卡尔曼滤波器增益的最优标准是使k时刻估计误差的方差和最小,即通过最小化E(JN)得到卡尔曼滤波器增益,这里的JN:
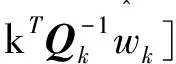
(14)

(15)
其中,代价函数的第一个α最小化当前时刻的协方差,这有利于滤波器最终收敛的状态估计值更接近于系统的新量测值;代价函数的第二个α只是为了方便数学处理,当进行最小化求值时认为常数。
改进后的卡尔曼滤波器增益:
(16)
估计误差协方差的滤波更新方程:
(17)
估计误差协方差的估值方程可表示:
Pk|k-1=α2kPk-1|k-KkHkPk-1|k
(18)
2.2 MAEKF控制结构
采用MAEKF的无位置传感器BLDCM控制方案结构如图1所示。

图1 MAEKF控制方案结构框图
该控制结构主要由转速PI控制、滞环电流控制、电机参数计算、MAEKF滤波器和BLDCM 5部分组成。通过采样三相绕组相电流(ia,ib,ic),经AD转化后计算三相绕组相电流并作为模型的输入,状态变量为三相绕组相电流、转速ω和电角度θ,并根据转子位置关系确定电机换相时刻。电角度与电机绕组和功率器件的工作关系如表1所述。

表1 电角度与电机绕组和功率器件的工作关系
2.3 仿真研究
在MATLAB/Simulink中建立基于MAEKF的BLDCM无位置传感器控制模型,该模型转速采用PI控制,电流采用滞环控制。电机起动后空载运行并在0.4 s时突加0.1 N·m的转矩负载。仿真结果如图2~图4所示。
负载转矩突变时刻电机转速、转矩和转子位置信号测量波形如图2所示。由图2可得,在负载转矩突变时电机转速突降,但在0.2 s时转速达到稳态值。电机响应时间等可通过PI控制器调节。
图3为电机在负载转矩突变时刻,三相电流ia,ib,ic与霍尔信号Ha,Hb,Hc波形图。由图3可得,负载转矩突增导致相电流幅值增大,相电流的周期变长,电流幅值增大导致电磁转矩提高实现平衡负载转矩。仿真结果表明:电机在负载转矩突变时刻能准确获取转子位置信号,电机没有出现失速、缺相运行的情况,说明该方法在电机负载转矩突变时刻仍可稳定运行。
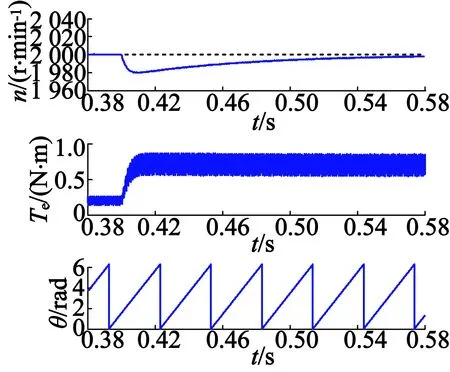
图2 负载转矩突变时刻电机转速、转矩和转子位置角波形

图3 负载转矩突变时刻相电流与霍尔信号波形
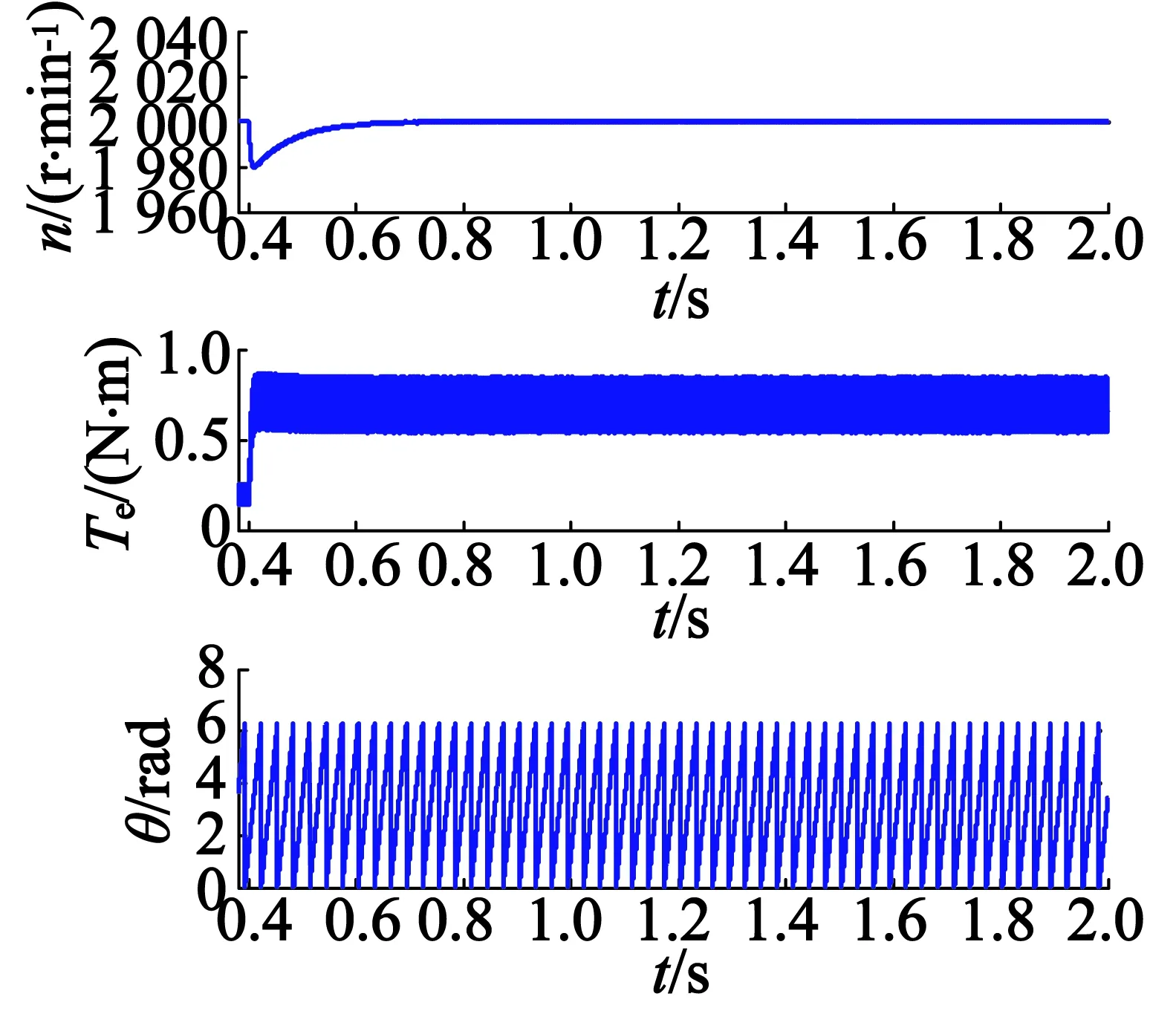
图4 带负载长时间运行的转速、转矩和转子位置角波形
在0.1 N·m的负载转矩下,电机长时间运行的转速、转矩和转子位置角关系如图4所示。负载转矩恒定时,电机的转速达到设定值,稳态误差为零;输出的电磁转矩为定值,输出的转矩纹波是由于换相时的相电流变化不连续导致的换相转矩脉动;测量的电机转子位置角变化连续。仿真结果表明了该系统在带负载长时间运行时也不会因为模型的精度问题导致系统发散。
电机在负载转矩突变和长时间带负载的过程中均没有失速的情况,转速、转矩和转子位置角输出连续,相电流与霍尔信号对应关系准确,MAEKF在负载转矩突变和恒定的工况下均能很好地估计电机转子位置,准确给出电机换相点,没有出现换相错误问题,仿真结果表明该方法具有较强的鲁棒性,验证了该方法的可靠性。
3 实验验证
以DSP处理器作为主控单元,以IGBT构成三相全桥驱动单元和一台星型连接无刷直流电机作为被控对象的实验系统平台上验证上述方法的正确性。该系统采用霍尔元件ACS758LCB将相电流转化为电压信号,转化后的电压信号经电压跟随器进行阻抗匹配后送入DSP数模转换模块,然后通过AD采样获得相电流的大小。实验样机参数:额定直流侧电压ud=24 V;额定转矩TN=0.18 N·m;额定转速nN=2 000 r/min;衰减因子α=1.036。
实验电机空载起动,自由加速到稳态后在0.4 s突加0.1 N·m的负载。实测电机的转速和负载突变时刻的相电流波形如图5、图6所示。

图5 实测电机转速波形

图6 负载转矩突变时刻的
在负载转矩突增时,相电流周期变长,相电流增大引起电磁转矩增大来平衡负载转矩;试验过程在负载转矩突变时刻没有产生转速突变和失步的现象。实验表明该方法在负载转矩突变时刻能很好地估算转子位置,实现准确换相。
电机霍尔信号和功率器件的动作关系如图7所示,从量测的波形可以看出,功率器件动作略迟滞于霍尔信号,迟滞时间非常短仅为数微秒。负载转矩突变虽然会引起转速的突降,并影响了相电流的波形,但是不会影响系统对转子位置角的估计,系统仍能准确给出换相点,实验结果验证了控制方法的可行性。

图7 电机霍尔信号和功率器件动作波形
4 结 语
本文提出了一种基于衰减卡尔曼滤波的无刷直
流电机无位置传感器控制方法,该方法通过量测电机的相电流,实现对电机转子位置角和转速的估算,经实验验证得到以下结论:
1)该方法在负载恒定、转矩突变时均能很好地给出转子位置信号,电机运行平稳,没有失速等不良现象;控制系统对电机参数摄动、模型误差等问题具有较强的鲁棒性;具有较高的可靠性和实用性。
2)该方法对电机参数、模型精度要求不高,但对参数测量准确性具有一定的要求。调试时可根据系统条件,调节衰减因子来均衡模型不精确和参数测量误差对系统的影响,实现系统最优。
[1] KIREE C,KUMPANYA D,TUNYASRIRUT S,et al.PSO-Based optimal PI(D) controller design for brushless DC motor speed control with back EMF detection[J].Journal of Electrical Engineering & Technology,2016(5):715-723.
[2] 潘积兰,余建成,刘二豪.无位置传感器无刷直流电动机位置误差分析及补偿[J].微特电机,2016,44(2):41-44.
[3] 郭子钊,佃松宜,向国菲.基于卡尔曼滤波算法的无刷直流电机直接转矩控制[J].科学技术与工程,2016,16(17):49-55.
[4] 吴耀春,韩向可.基于MCP8025的无位置传感器无刷直流电机控制系统设计[J].微特电机,2016,44(9):83-85.
[5] 殷帅,马铁华,吕彩琴.线电压确定无刷直流电动机转子位置新方法[J].微特电机,2016,44(2):37-40.
[6] TERZIC B,JADRIC M.Design and implementation of the extended Kalman filter for the speed and rotor position estimation of brushless DC motor[J].IEEE Transactions on Industrial Electronics,2002,48(6):1065-1073.
[7] 林海,严卫生,林洋,等.双扩展卡尔曼滤波的无刷直流电机无传感器控制[J].西北工业大学学报,2010,28(2):197-201.
[8] 史婷娜,张倩,夏长亮,等.基于UKF算法的无刷直流电机转子位置和速度的估计[J].天津大学学报,2008,41(3):338-343.
[9] 林益平.基于EKF相位增益校正的无传感器BLDCM速度控制[J].电气传动,2007,37(6):12-15.
[10] BRUNSBACH B J,HENNEBERGER G,Brunsbach B J,et al.Field-oriented control of an induction motor without mechanical sensors using a Kalman-Filter[J].Archiv Für Elektrotechnik,1990,73(5):325-335.
[11] 郭鸿浩,周波,刘颖,等.永磁无刷直流电机角加速度估计[J].电工技术学报,2014,29(5):93-103.
[12] 蔡佳,黄长强,井会锁,等.基于指数加权的改进衰减记忆自适应滤波算法[J].探测与控制学报,2013,35(4):21-26.
[13] 高伟,叶攀,许伟通.改进的自适应衰减卡尔曼滤波算法[J].计算机测量与控制,2016,24(8):190-192.
[14] 曲毅,刘忠,孙世言.纯方位被动目标运动分析的衰减记忆卡尔曼滤波算法[J].武汉理工大学学报(交通科学与工程版),2006,30(5):817-819.

