基于两段卡尔曼滤波的永磁同步电机磁链在线辨识

韩晓燕，刘秀敏

(中原工学院信息商务学院， 郑州 450007)

0 引 言

永磁同步电机(以下简称PMSM)近年来在机器人、电动汽车、家电等领域获得越来越广泛的应用[1]。相比于异步电机，PMSM的功率密度更大、效率更高，而且少了转差之后控制也更加简单。

无论是PMSM的无位置传感器控制、最大转矩电流比控制，还是依赖模型的其他控制算法，都需要知道准确的永磁体磁链参数ψr。近年来，许多学者致力于PMSM的在线参数辨识以提高电机的控制性能[2-5]。文献[2]采用遗传算法来估计PMSM的4个参数，包括了ψr，收获了良好的辨识结果。文献[3]采用模型参考自适应同时估计电机的4个参数，并依据Lyapunov稳定性设计了4个自适应律，但同时估计这么多参数会导致算法的收敛速度很慢，甚至无法收敛。文献[4]也是通过模型参考自适应同时辨识了R和ψr，同时，分析了逆变器的非线性产生的电压测量误差对辨识结果的影响。

文献[5-6]中以交直轴的电流和磁链为状态方程构造了四阶经典卡尔曼滤波(以下简称KF)算法，获得了磁链在d，q轴下的分量。相比于模型参考自适应等算法，卡尔曼滤波的收敛速度更快、精度更高，而且对噪声的鲁棒性也更好，但同时也由于高阶逆矩阵的求解存在运算量大的问题，进而导致硬件成本增加。针对该问题，有学者尝试将高阶卡尔曼滤波进行分解降阶处理来减少运算量，从而在形式上构造了两段卡尔曼滤波器(以下简称TSKF)[7]。为了得到和分解前的卡尔曼滤波器完全等价的两段卡尔曼滤波器形式，文献[8]在TSKF的基础上提出了最优TSKF[8]。近年来，TSKF也被应用到了电机控制中，文献[9-10]将其用于PMSM的无传感器控制，对转子的位置进行了观测。本文提出基于两段卡尔曼滤波的PMSM在线磁链辨识方法，在文献[6]的基础上用TSKF代替KF，将四阶KF分解成2个二阶KF：一个全阶KF和一个增广KF，其中增广KF的状态变量就是需要辨识的交直轴磁链。实验结果表明，采用了TSKF后，减少了运算量，同时准确获得了永磁体磁链参数。

1 电机模型的建立

假设磁路不饱和，磁场呈正弦分布，忽略铁耗，那么PMSM在d,q轴下的电压：

(1)

式中:ud,id,Ld和uq,iq,Lq分别是d,q轴的定子电压、定子电流和定子电感;R是定子电阻;ω是转子转速;ψr是转子磁链。

在PMSM的运行中，不同工况下，由于温度等因素的影响，永磁体磁链ψr的幅值和方向会发生变化，如图1所示，从而将式(1)改写：

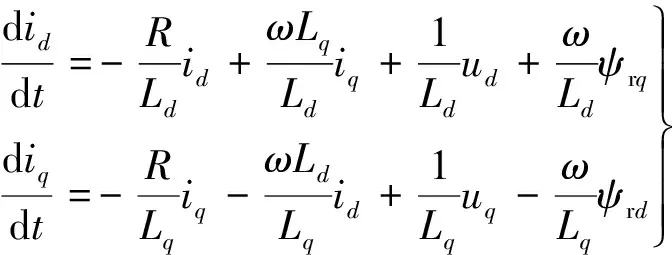
(2)

图1 PMSM磁链变化示意图

由于磁链随温度变化的速度比较缓慢，因此可认为其在一个采样周期内为恒定值，即:

(3)

将式(2)写成状态方程的形式：

(4)

若采样周期为T，则式(4)可以离散化为式(5):

(5)

2 基于卡尔曼滤波的磁链辨识

2.1 经典卡尔曼滤波

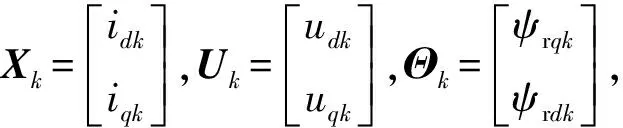
为了利用卡尔曼滤波进行磁链的在线估计，将磁链ψrd,ψrq作为状态变量加到式(5)中，可以得到四阶的卡尔曼滤波模型：

(6)

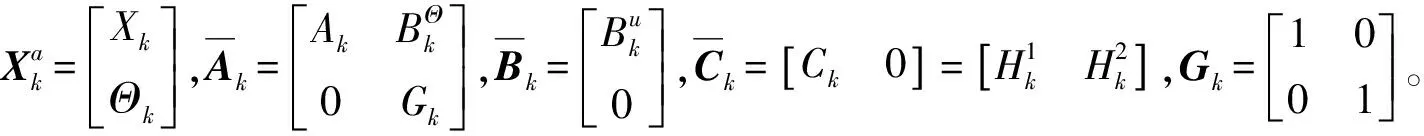
根据式(6)，可以采用经典的卡尔曼滤波进行状态变量的观测，算法如下：

(7)

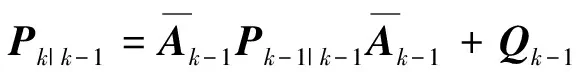
( (8)

( (9)

( (10)

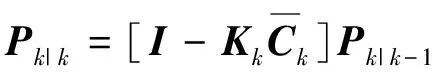
(11)

采用式(7)～式(11)的经典卡尔曼滤波算法时，状态相量为四阶，输入相量和输出相量均为二阶，此时运算量大，需要消耗较多的硬件资源。

2.2 两段卡尔曼滤波

(12)

(13)

将式(13)代入到式(7)～式(11)中，就可以得到如下的TSKF更新算法。

第一个方程组为更新状态相量的预测值：

(14)

第二个方程组为更新状态相量的最优估计：

(15)

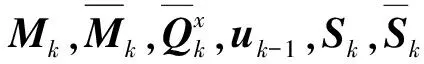
TSKF的初始估计值和初始协方差矩阵也可以由以下关系得到：

(16)

经过式(14)～式(16)的变换过程，原来的四阶卡尔曼滤波器就分解为2个二阶的卡尔曼滤波器，两者在数学上是完全等价的。但相比之下，状态相量为二阶，输入相量和输出相量均为二阶的TSKF却能在运算量上比四阶的经典卡尔曼滤波器减少很多。文献[10]指出，相比于四阶KF，二阶TSKF的乘法运算量减少了20.3%，加法运算量减少了22.5%，因此可以减少运算时间、降低硬件成本。实际应用中，由于式(14)～式(16)中有很多零矩阵，因此TSKF的运算时间要比理论上更加短。

3 实验验证

基于TSKF的PMSM磁链在线辨识框图如图2所示。电机参数如下：额定电压310 V，额定电流1.5 A，额定转速4 500 r/min，定子电阻2.7 Ω，d轴电感42 mH，q轴电感71 mH，永磁体磁链ψr=0.34 Wb。控制芯片采用TI公司的TMS320F28335，时钟频率设为150 MHz。实验结果如图3～图5所示。

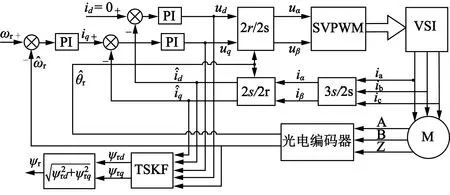
图2 基于TSKF的PMSM磁链辨识框图

(a) 转速指令

(b) 永磁体磁链辨识结果

图3不同转速下的磁链辨识实验

(a) 经典KF的运算时间

(b) TSKF的运算时间

图4KF和TSKF运算时间对比实验

图5 3 000 r/min时的电流波形

同时可以看到，辨识结果要比实际值略高，且转速越高，辨识结果越接近实际值。这是由于逆变电路的非线性导致的，转速越高，非线性的影响越小。

图4对比了经典KF算法和TSKF算法的程序运行时间。驱动器的开关频率设为5 kHz，算法运行周期为200 μs。其中经典KF算法用时89.6 μs，TSKF算法用时68.3 μs。采用TSKF能够节省23.8%的运算时间，该实验验证了TSKF算法的实用性。

4 结 语

本文针对PMSM的永磁体磁链辨识，提出一种基于两段卡尔曼滤波的在线辨识算法。首先构建了以交直轴电流和磁链为状态变量的四阶经典卡尔曼滤波器，然后利用变换矩阵将其分解为2个二阶卡尔曼滤波器，变换后的两段卡尔曼滤波器减少了运算时间，从而能够降低硬件成本。最后，实验结果验证了该算法的有效性和实用性。

[1] 王成元,夏加宽,杨俊友,等.电机现代控制技术[M].北京：机械工业出版社,2006.

[2] 肖曦,许青松,王雅婷,等.基于遗传算法的内埋式永磁同步电机参数辨识方法[J].电工技术学报,2014,29(3):21-26.

[3] 陈振锋,钟彦儒,李洁.嵌入式永磁同步电机自适应在线参数辨识[J].电机与控制学报,2010,14(4):9-13.

[4] KAN L,ZHU Z Q,QIAO Z,et al.Influence of nonideal voltage measurement on parameter estimation in permanent-magnet synchronous machines[J].IEEE Transactions on Industrial Electronics,2012,59(6):2438-2447.

[5] SHI Y C,SUN K, HUANG L P,et al.Online identification of permanent magnet flux based on extended Kalman filter for IPMSM drive with position sensorless control[J].IEEE Transactions on Industrial Electronics,2012,59(11):4169-4178.

[6] 史宇超,孙凯,马鸿雁,等.内埋式永磁同步电机永磁磁链的在线辨识[J].电工技术学报,2011,26(9):48-53.

[7] FRIEDLAND B.Treatment of bias in recursive filtering[J].IEEE Transactions on Automation Control,1969,14(4): 359-367.

[8] HSIEH C S,CHEN F C.Optimal solution of the two-stage Kalman estimator[J].IEEE Transactions on Automatic Control,1999,44(1):194-199.

[9] 易伯瑜,康龙云,陶思念,等.基于两段卡尔曼滤波器的内置式永磁电机观测器设计[J].电工技术学报,2014,29(9):110-118.

[10] 易伯瑜,康龙云,林玉健,等.基于双段卡尔曼滤波的永磁电机无传感器控制[J].华南理工大学学报 (自然科学版),2013,12(10):49-55.