初级分段永磁直线电机段间无传感器控制研究
辛忠有,李立毅,刘家曦
(哈尔滨工业大学,哈尔滨 150001)
0 引 言
长初级永磁直线电机只在初次级相互耦合的区域产生电磁推力,因此可以将初级设计成多段紧密相连的结构,段与段之间的初级绕组是断开的,只给与动子耦合的初级绕组通电,这样既能够改善长初级同时通电带来的铜耗过大问题,同时也可以使电机初级的设计模块化,简化了加工与装配的难度,在轨道交通、舰载弹射等长行程直线运动领域具有广阔的应用前景。然而由于该类电机特殊的工作环境以及行程过长,使其很难安装位置传感器,因此越来越多的学者关注初级分段电机无传感器技术的研究。
目前无传感器技术的研究主要集中在旋转电机上,有以下几种方式。一种是利用电机的凸极效应,通过注入特定频率的信号来获取电机的位置信息;另一种是利用观测器方法,从电机的电流和电压得到反电势,并利用反电势估算位置和速度。由于初级分段电机过渡区域电路不连续,动子和定子之间的耦合面积持续变化,电感、永磁体磁链等电机参数大范围变化,上述方法应用到分段电机上,需要考虑过渡区域如何进行有效的位置和速度的估算。
初级分段电机的数学模型和控制策略方面,文献[1-2]分析了分段电机过渡区域电磁参数的变化规律,并建立了多段初级电机驱动系统的变参数动态模型,文献[3-5]给出了过渡区间驱动控制算法和切换方法;无传感器控制方面,文献[5-8]研究了基于反电势状态观测器的位置估算方法,并且实现了过渡区域的平稳切换,文献[9]提出了应用于长初级直线同步电机的基于高频注入的无传感器控制方法。
本文在上述文献研究的基础上,首先给出了分段电机过渡区间电磁参数变化规律的数学模型;在段内区域应用扰动观测器实现了反电势观测,并在此基础上提出了利用双段定子的合成反电势进行段间区域位置估算的方法;然后构建了基于电机动力学方程的全阶Leunberger速度观测器,并且给出了分段电机无传感器控制系统的原理框图;最后通过仿真和实验研究,验证了所提方法的正确性和有效性。
1 段间区域电磁参数变化规律
初级分段永磁直线电机结构简图如图1所示。

图1 初级分段永磁直线电机结构简图
初级分段永磁直线电机在动子完全与某一段初级耦合(段内区域)时,其电磁方程与传统的永磁直线同步电机类似。当动子同时和两段初级耦合(段间区域)时,电机的电磁参数,主要包括同步电感、永磁体耦合磁链、反电势系数和电磁推力系数,与动子的实际位置(动子和每段定子的耦合程度)有关。因此,建立初级分段永磁直线电机的数学模型,有必要研究动子处于段间区域时,电机电磁参数随动子位置的变化关系。
为了简化分析,认为动子处于段间区域,电磁参数随动子位置近似成线性变化,即某一段定子的一项电磁参数的幅值和动子与该段定子的耦合面积成线性关系。根据图1的动、定子之间的关系,第n段定子的永磁体耦合磁链、同步电感随动子位置变化规律可表示:
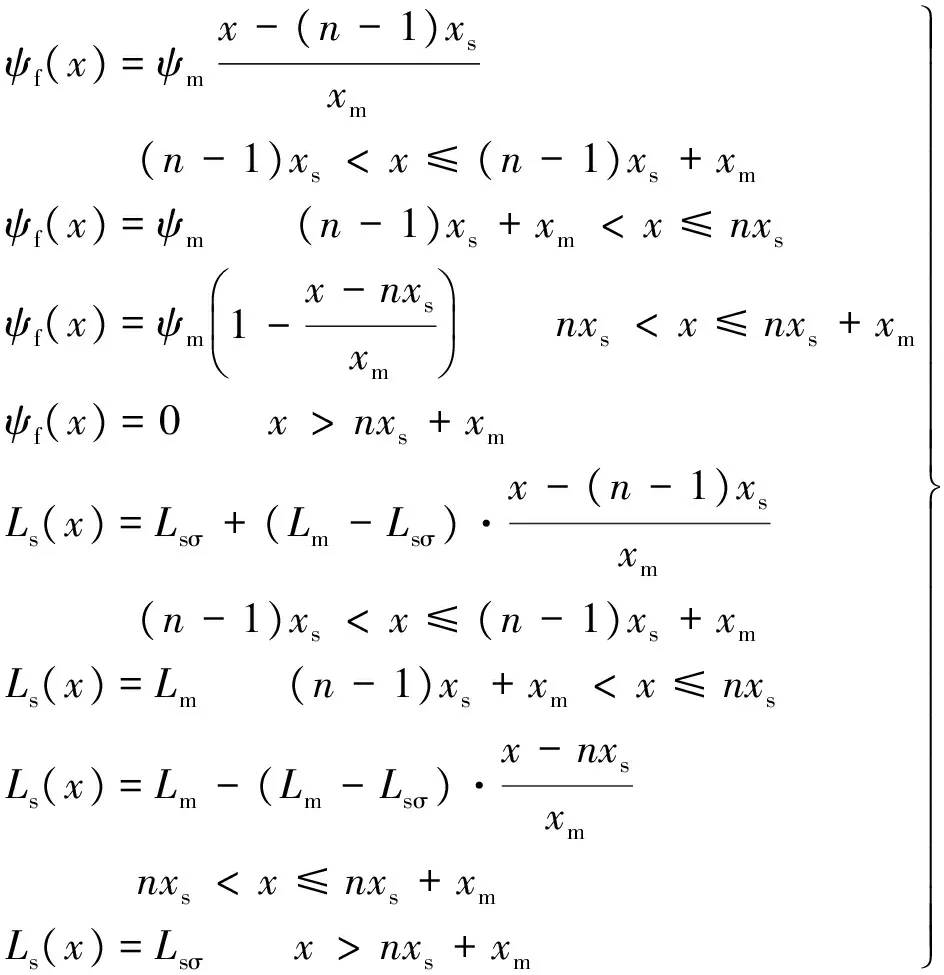
(1)
式中:n代表定子段数;x为动子和分段电机起点之间的距离;xs为单段定子的长度;xm为动子的长度;ψm,Lm为动定子完全耦合时永磁体励磁磁链和同步电感的幅值;Lsσ为动子不与定子耦合时同步电感的幅值,即漏感值。4个表达式分别表示动子进入该段定子(开始与该段定子耦合),动子完全与该段定子耦合,动子退出该段定子和动子完全退出该段定子4个过程。
以上给出了初级分段电机段间区域电磁参数的数学模型,而段间区域可结合段间电磁参数的数学表达式,直接采用普通永磁同步电机的电压方程和动力学方程。正如前文所述,初级分段电机采用分段供电方式,每段定子配有独立的驱动单元,当动子处于段内区域时,该段定子的驱动单元工作,当动子处于段间区域时,则需两段定子的驱动单元同时工作以保证段间区域合成推力与段内区域相等,使动子能够平稳过渡。初级分段电机通常采用id=0的矢量控制。
2 无传感器技术
2.1 反电势观测器
直线电机控制系统中,滑模观测器是一种常用的无传感器控制方法[9-11],但其存在抖振的问题。本文提出一种基于扰动观测器的反电势观测方法,能够有效地改进滑模观测器方法存在的非线性问题,并且易于进行角度补偿,估算位置更准确。针对分段电机段间定子电路不连续的特点,采用两个反电势观测器分别进行观测,再将各段的观测反电势相加,从合成反电势中提取出位置信息,进而估算出电机的角度。
为了建立观测器方程,应从电机的状态方程入手。若采用等幅值变换,表贴式永磁直线同步电机在α-β坐标下的电压方程:
(2)

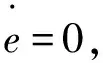
(3)
式中:A11=-(Rs/Ls)I=a11I,A12=-(1/Ls)I=a12I,B1=(1/Ls)I=b1I,I为单位阵。
建立如下的观测器:
(4)
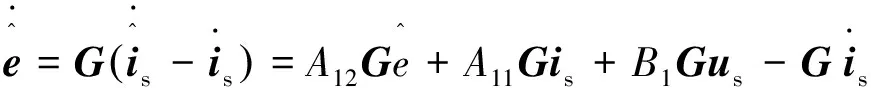
(5)
(6)

(7)
代入式(5)中,有:
(8)
式(8)为改进的反电势观测器,不含有电流的导数,更适用于实际应用场合,其原理框图如图2所示。
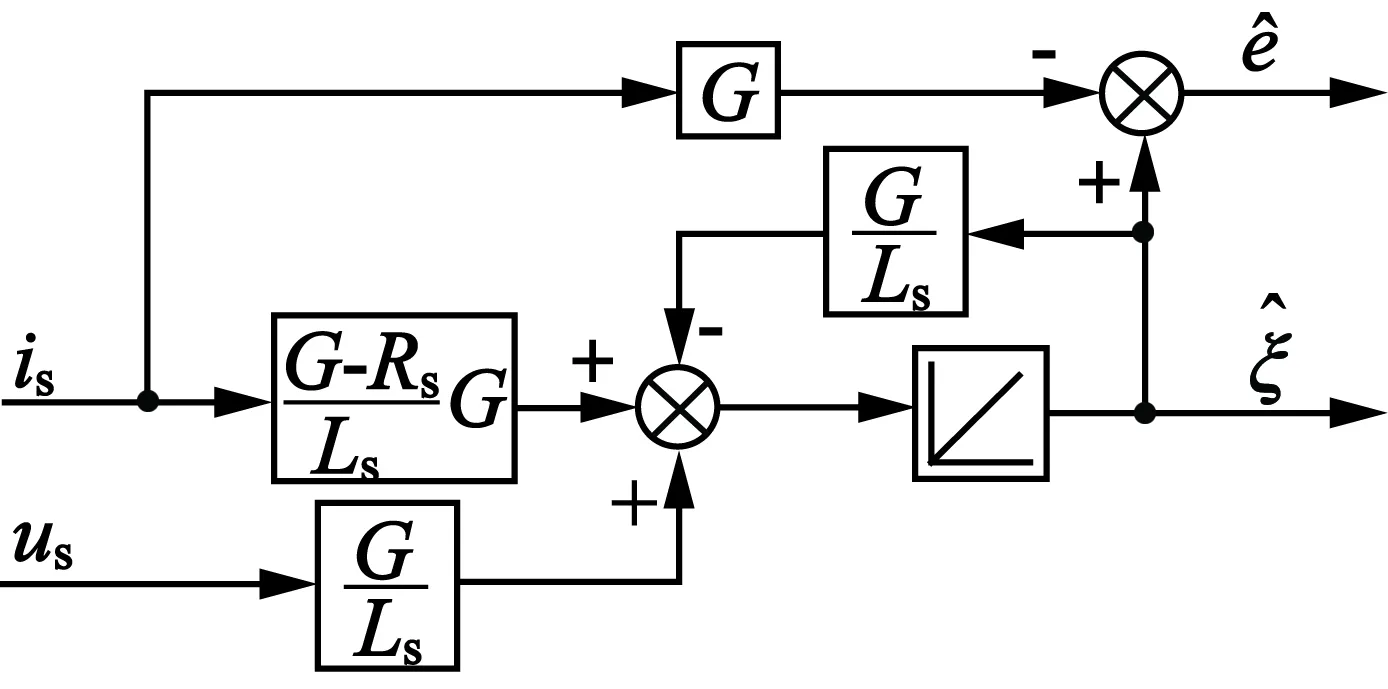
图2 扰动观测器原理框图
以上为初级分段直线电机段内区域反电势观测方法,当动子处于段间区域时,本文采用以下方案:相邻段建立各自的反电势观测器独立进行观测,并将观测反电势相加,由合成反电势估算动子位置。
从电机的角度来看,不论是处于段内区域还是段间区域,电机都要保持稳定的速度和推力向前运行,其动力学方程与动子所在的位置无关,因此可将段间区域视为一段“虚拟段[13]”,其永磁体励磁磁链和反电势为两段电机的对应值相加。“虚拟段”的合成磁链用ψf表示,ψf1和ψf2为段间区域相邻2个定子段S1和S2的永磁体磁链,因此:
ψf=ψf1+ψf2
(9)
将式(1)的过渡区间的永磁体磁链代入,可以得到S1和S2的反电势:
(10)
因此“虚拟电机”的合成反电势:
(11)
可见,合成反电势表达式与动子处于段内区域的反电势表达式:
(12)
相同,因此可以通过提取合成反电势中的角度信息进行段间位置估算。
2.2 观测器极点配置
(13)

(14)
由式(14)和式(5)可以得到实际的反电势观测误差方程:

(15)


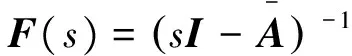
(16)
观测误差和反电势的比值(误差比率)的上界可由F(s)的无穷范数得到:
‖F(s)‖
(17)
‖F(s)‖
(18)
式(18)中,σmax[·]为矩阵的最大奇异值。从式(17)和式(18)可以得:
(19)
可以看出,误差比率的范围取决于动子的速度和观测器的极点。若令误差比率满足:
(20)
则观测器的极点配置和反馈增益:

(21)

(22)
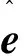

(23)
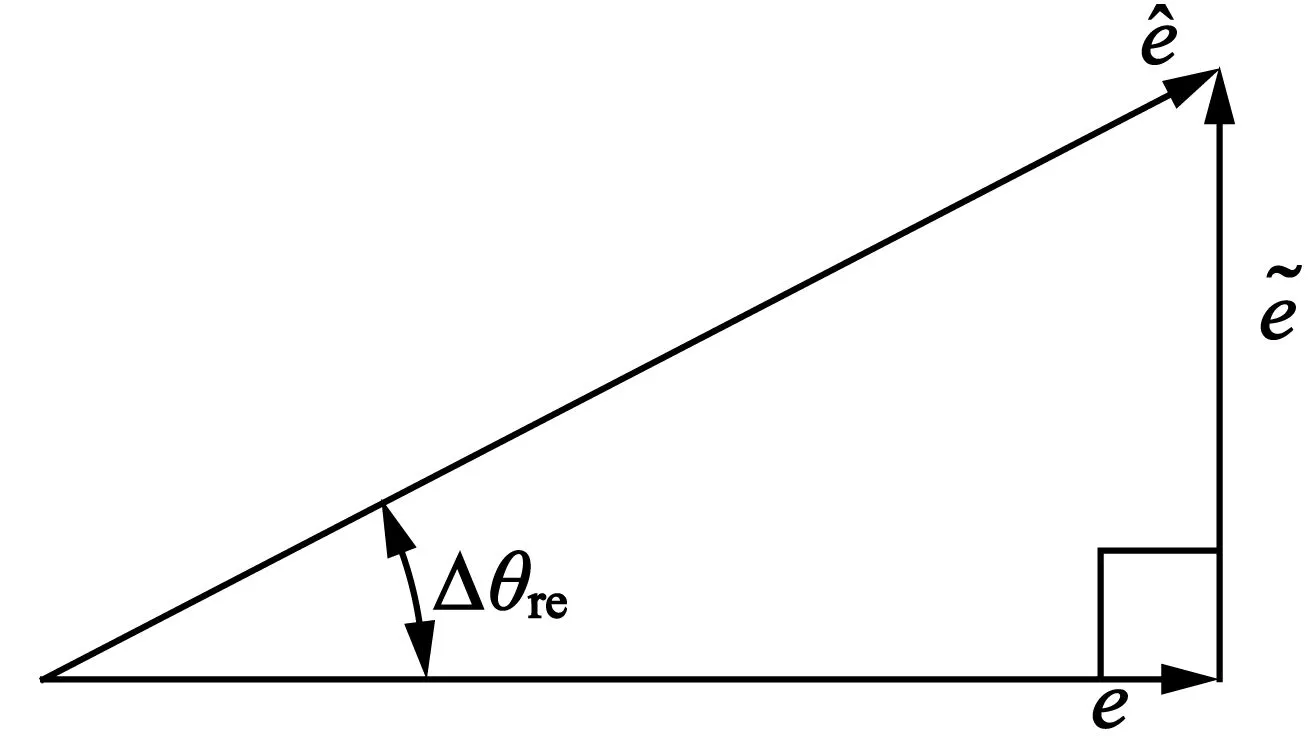
图3 观测误差矢量图
2.3 位置和速度估算
通过反电势估算动子位置和速度方法包括开环计算法[14]、自适应速度观测法[15]及锁相环法[16]等,这些方法都是基于对电机电路方程的推导或观测,对于普通的永磁直线同步电机和初级分段电机的段内区域比较适用,而且估算精度较高。但是对于分段电机的段间区域,由于两段定子之间电路是不连续的,因此用电机的电路方程来估算速度,会产生较大的波动。这种波动是反馈通道的扰动,无法通过前向通道的控制方法来消除,而且会对电机的速度闭环产生很大的影响,进而影响电机的闭环性能。
本文考虑采用基于电机动力学方程的全阶Luenberger观测器的速度观测方法,可以有效地减弱采用电路方程估算带来的速度波动;并且可以通过调整观测器的增益,配置观测器的极点,提高动态性能;观测器在观测速度的同时,可以实现对负载推力的观测,利用观测的负载推力,对参考推力(q轴电流给定)进行前馈补偿,可以提高速度环抵抗负载推力扰动的能力,从而提高系统的控制性能。
初级分段永磁直线同步电机的动力学方程:
(24)
式中:Fe为电机的电磁推力;Fl为电机负载推力;M为电机动子质量;B为与动子速度相关的摩擦系数。
如果把负载推力也视为状态变量,近似认为负载推力缓慢变化,即Fl满足式(25),则可实现对电机位置、速度和负载推力的同时观测,建立的全阶Leunberger观测器如式(26):
(25)

(26)
式中:c为反馈校正量;l1,l2和l3为反馈系数。下面讨论反馈校正量如何选取。



(28)
可见,所选取的反馈校正量为真实量和观测量的差值,全阶Leunberger观测器构建完成,其原理框图如图4所示。观测器状态方程能观,故可以任意配置极点。反馈系数l1,l2和l3可利用MATLAB中的acker( )函数来配置。
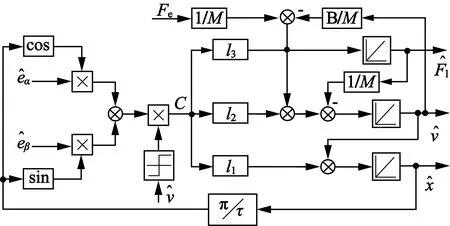
图4 全阶速度观测器原理框图
3 仿真及实验研究
图5为基于本文所提出的无传感器方法的初级绕组分段电机控制系统原理框图,据此用MATLAB/Simulink进行仿真研究,电机分成2段,参数如表1所示。

图5 初级绕组分段电机无传感器控原理框图

参数数值极对数p2极距τ/mm58.2单段定子长度xs/mm582动子长度xm/mm232.8定子电阻Rs/Ω4.8定子电感Ls/mH35漏感(动定子不耦合)Lsσ/mH28动子质量M/kg4摩擦系数B/(kg·m2s-1)0.04反电势系数K/[V·(m·s-1)-1]47.5推力系数KF/(N·A-1)142.5额定与过载推力Fe,Fm/N200,400额定与峰值电流Ie,Im/A2.5,5额定输出功率P/W400直流母线电压U/V310
仿真条件:电机速度v=2m/s,负载推力Fl=200N,母线电压为310V,逆变器开关频率20kHz。
仿真得到的定子段I的观测反电势波形如图6所示,定子段II的观测反电势波形如图7所示,合成反电势波形如图8所示。图中,0~0.18s动子处于定子段I;0.18~0.32s动子处于段间区域;0.32~0.5s动子处于定子段II。可见合成反电势和段内过程中反电势幅值和相位相同,用合成反电势获取段间位置的方案可行。
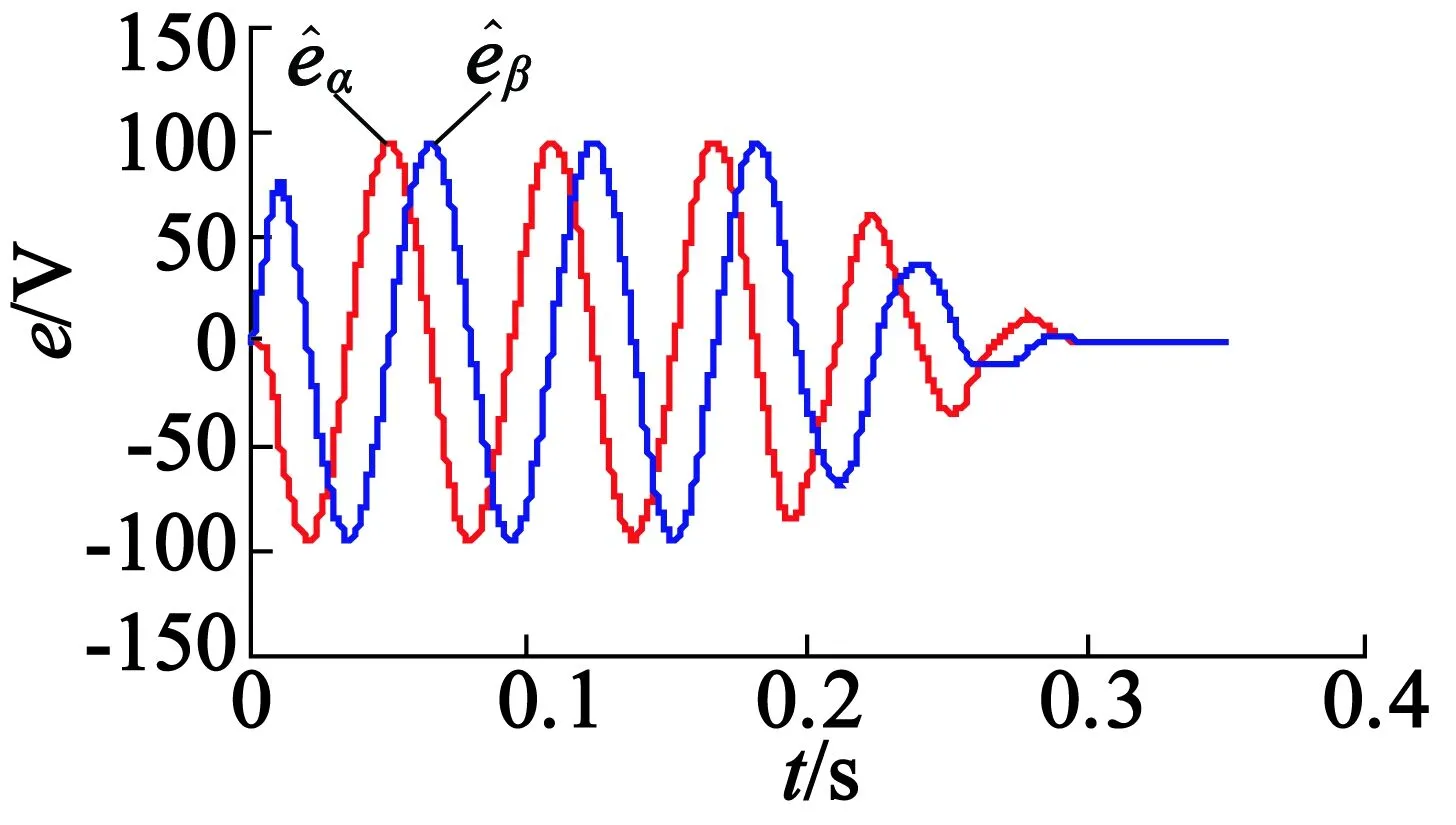
图6 定子段I的观测反电势
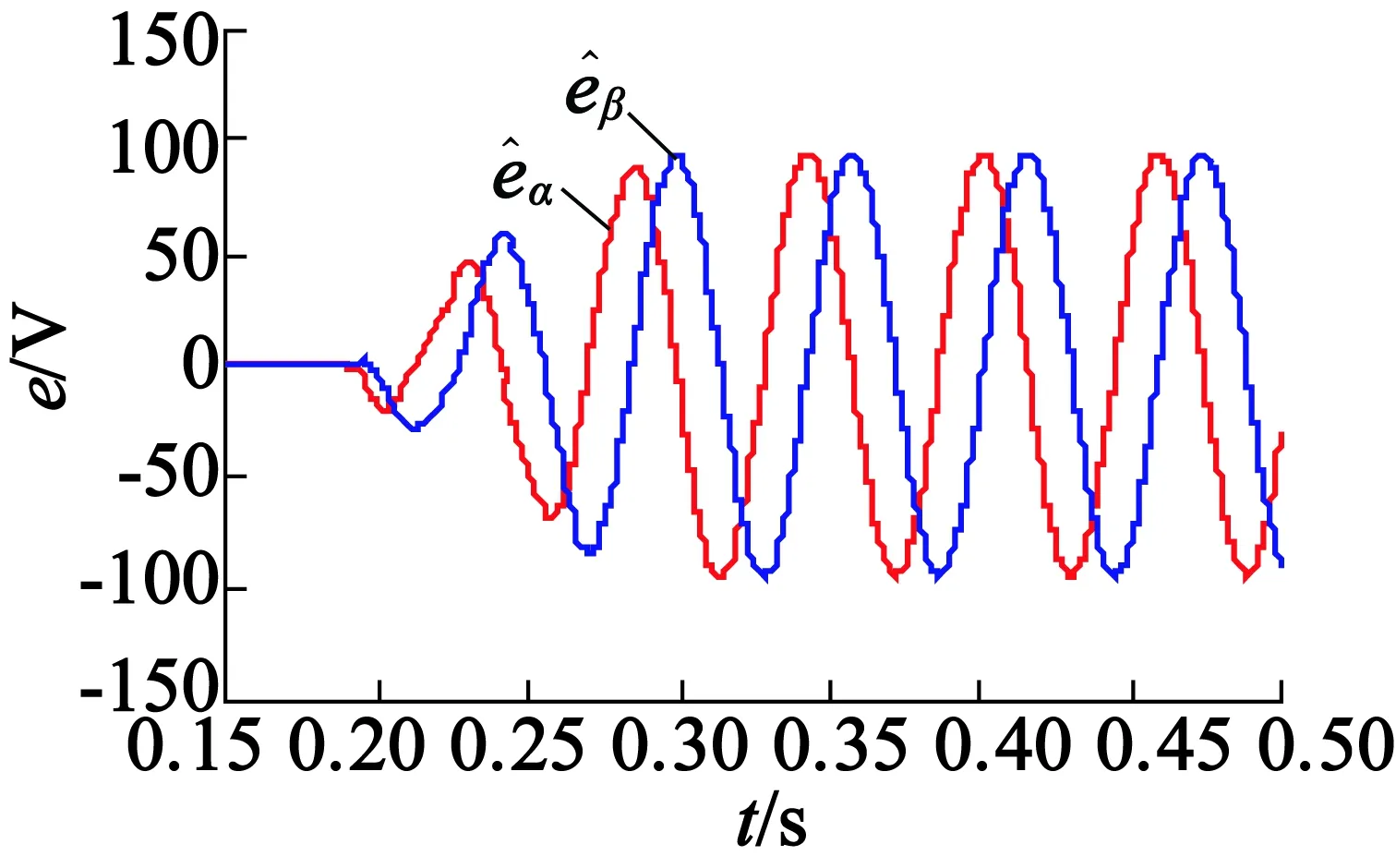
图7 定子段II的观测反电势
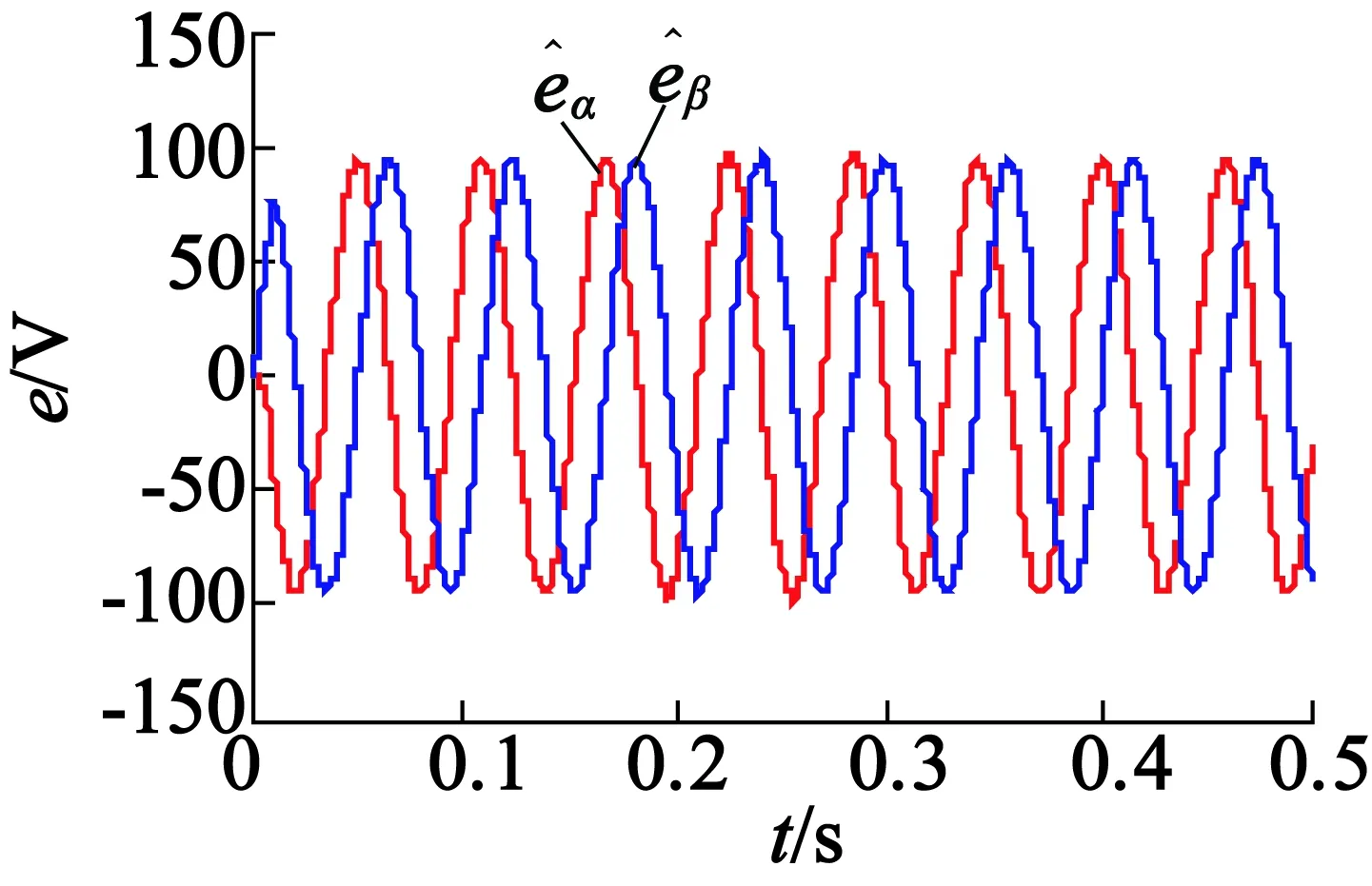
图8 两段定子合成反电势
用合成反电势进行电机位置和速度估算,电机速度指令为2m/s的阶跃响应,额定负载推力的条件下得到的真实位置θr、估算位置θg和位置估算误差Δθ如图9所示,得到的真实速度nr、估算速度ng和速度估算误差Δn如图10所示。可见,采用本文提出的无传感器算法得到的估算位置与真实位置的误差小于0.03rad,即0.56mm;估算速度与真实速度的误差在电机起动阶段较大,为0.1m/s;段内运行阶段,误差很小;段间过渡过程中,速度误差小于0.02m/s。为了更详细验证算法在段间区域的适用性,分别给出段间加速和减速情况下的仿真结果。段间区域电机速度指令为10m/s2的仿真结果如图11所示,可见段间加速过程中,速度误差有所增大,但小于0.03m/s;段间区域电机速度指令为-10m/s2的仿真结果如图12所示,可见减速过程中,速度误差为-0.03m/s,验证了无传感器方法的有效性。
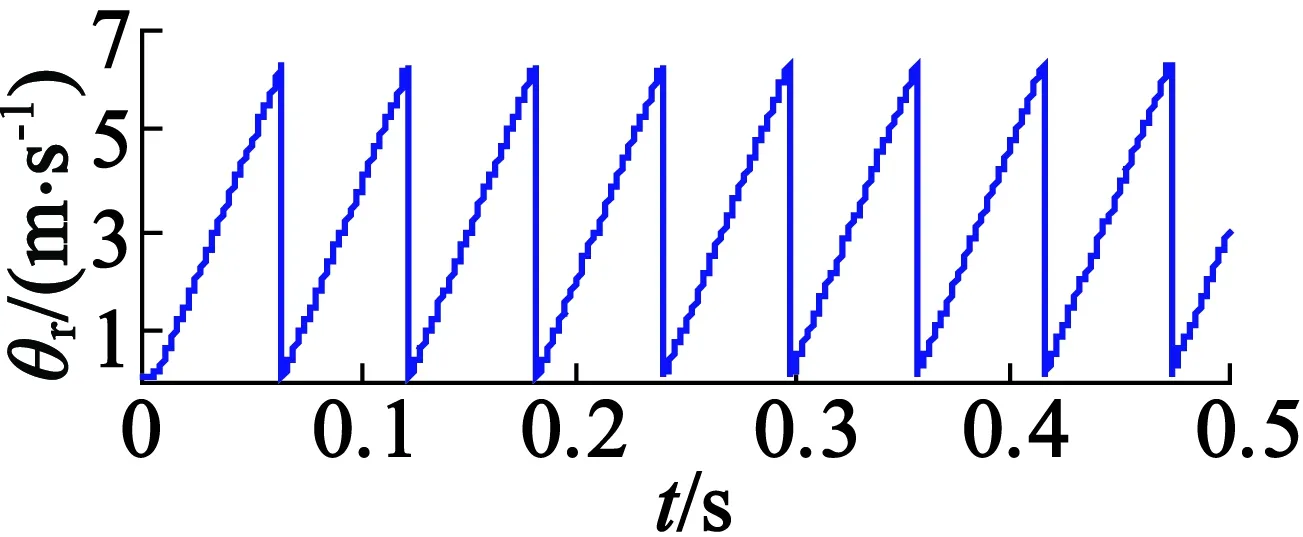

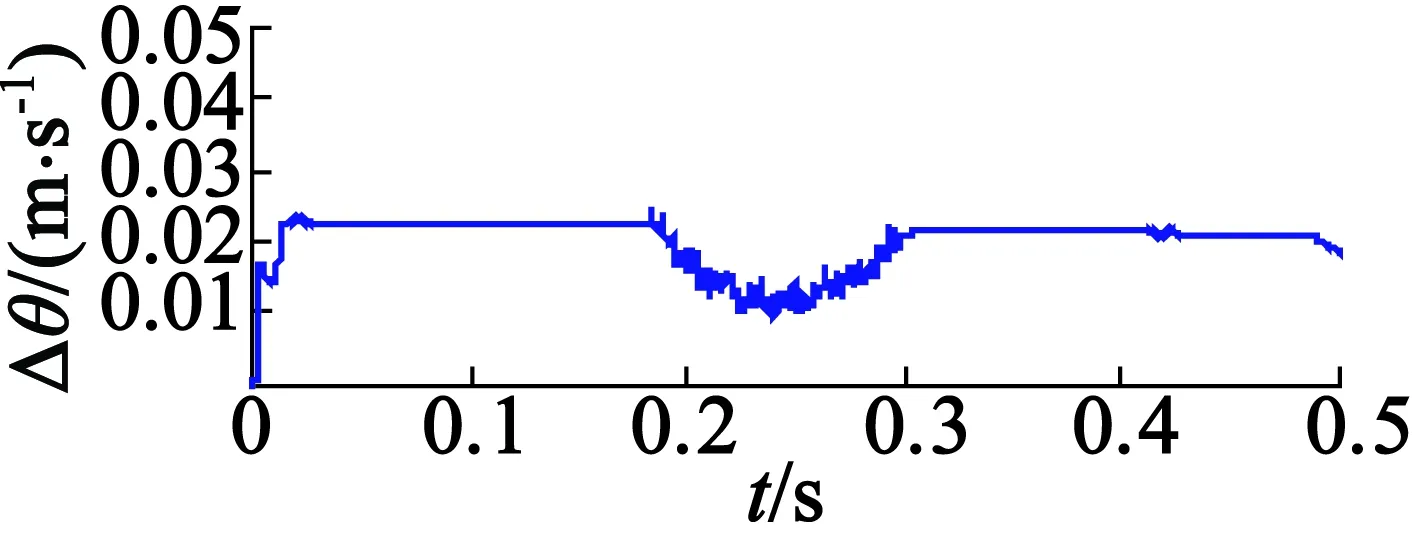
图9 真实位置、估算位置和位置估算误差

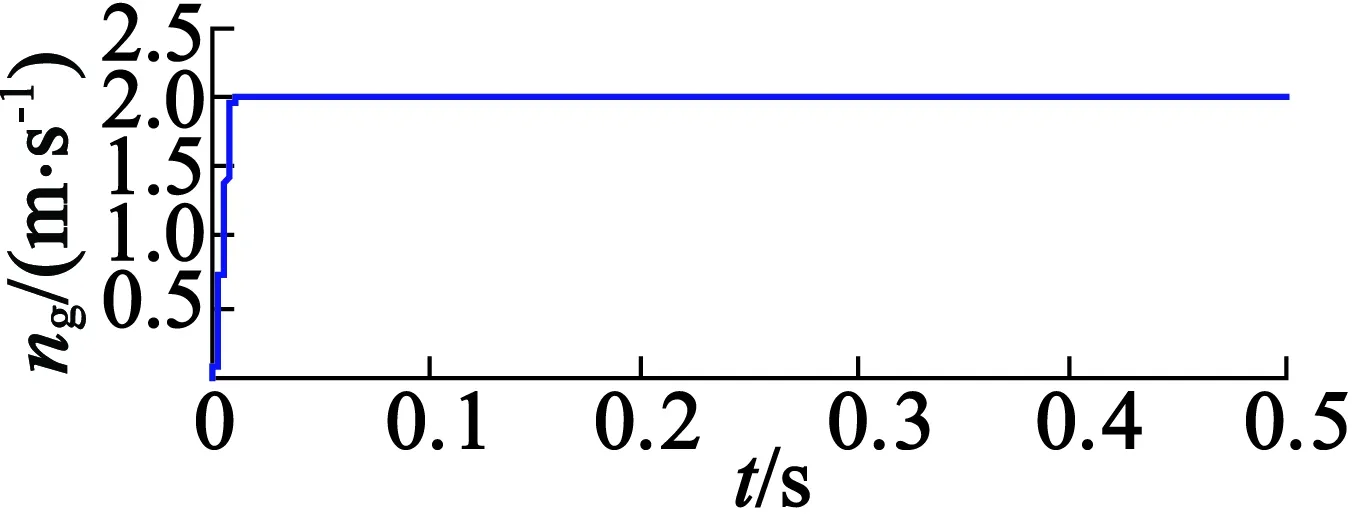
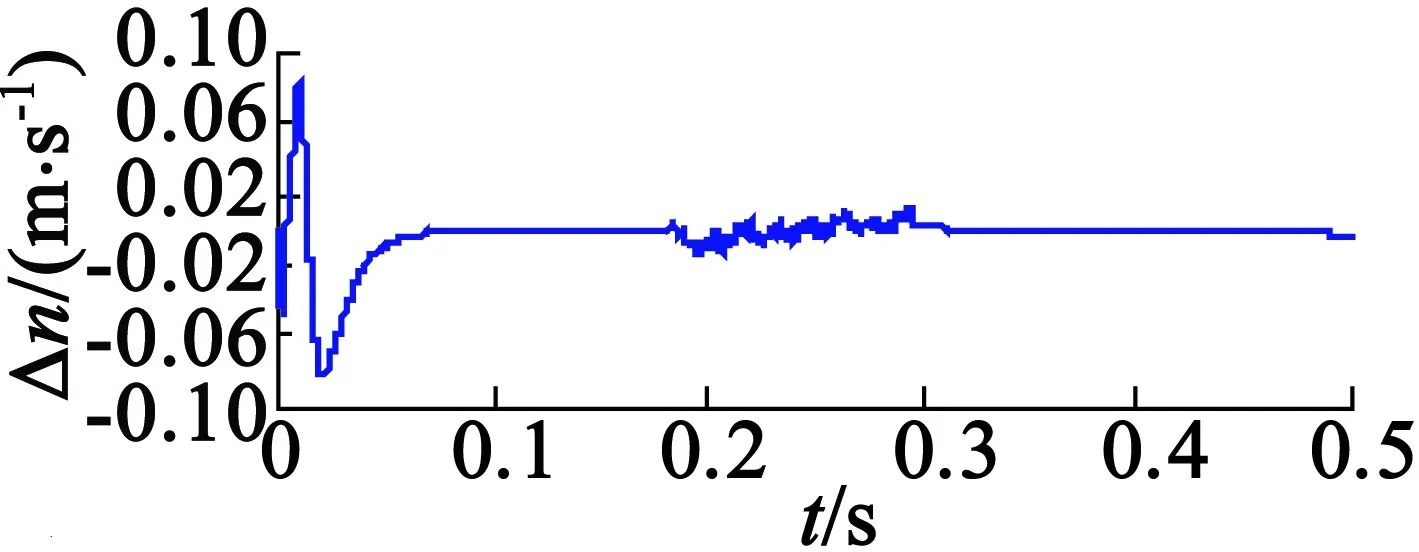
图10 匀速给定真实速度、估算速度速度估算误差

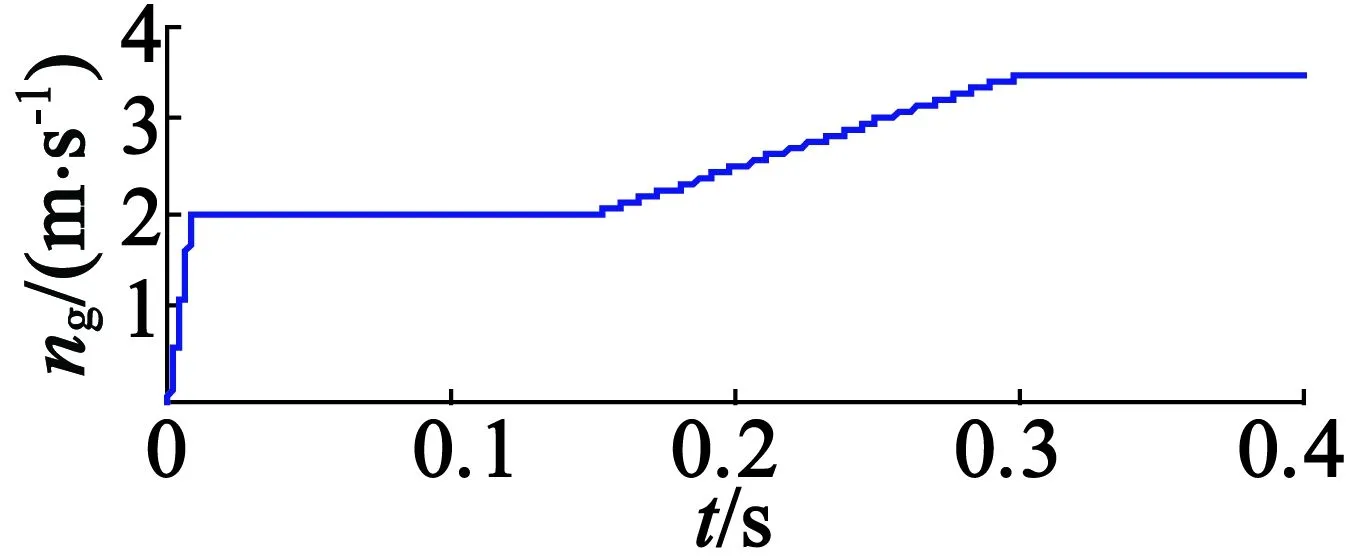
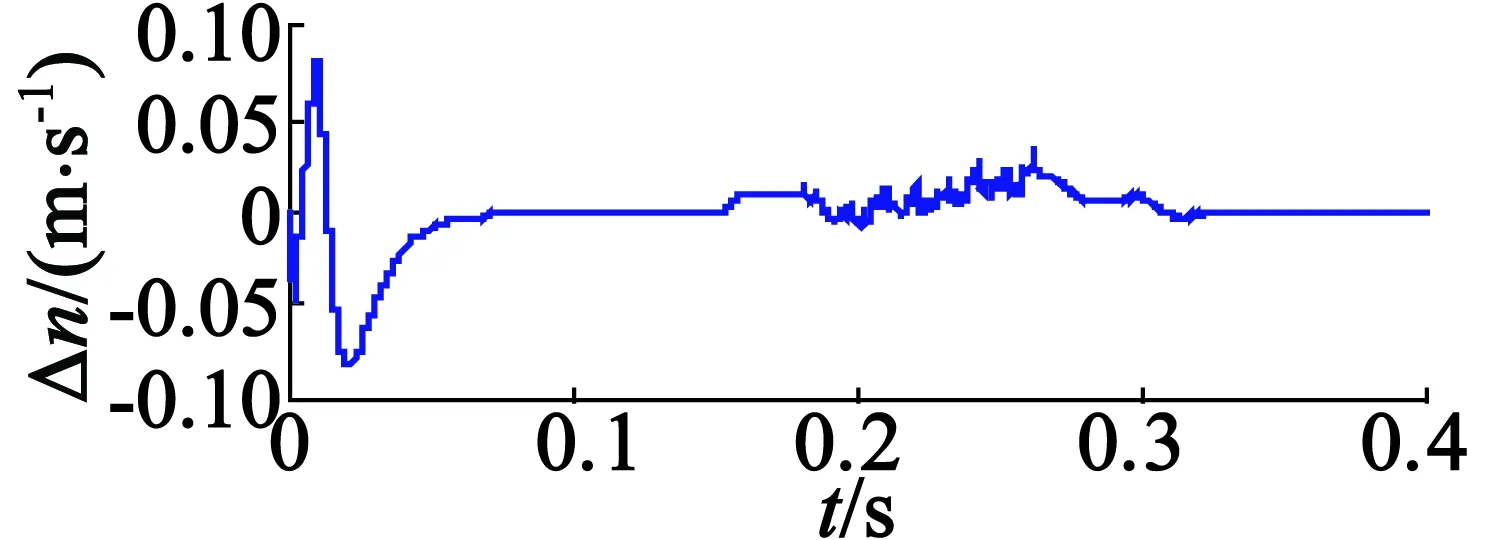
图11 加速给定真实速度、估算速度速度估算误差
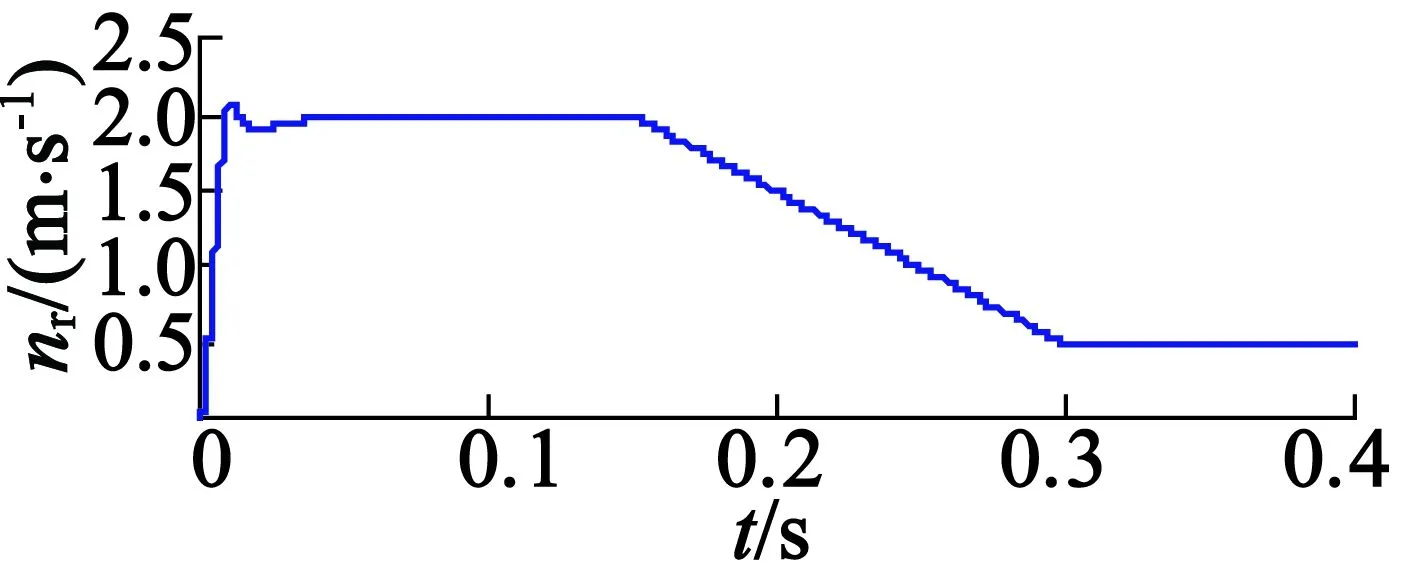
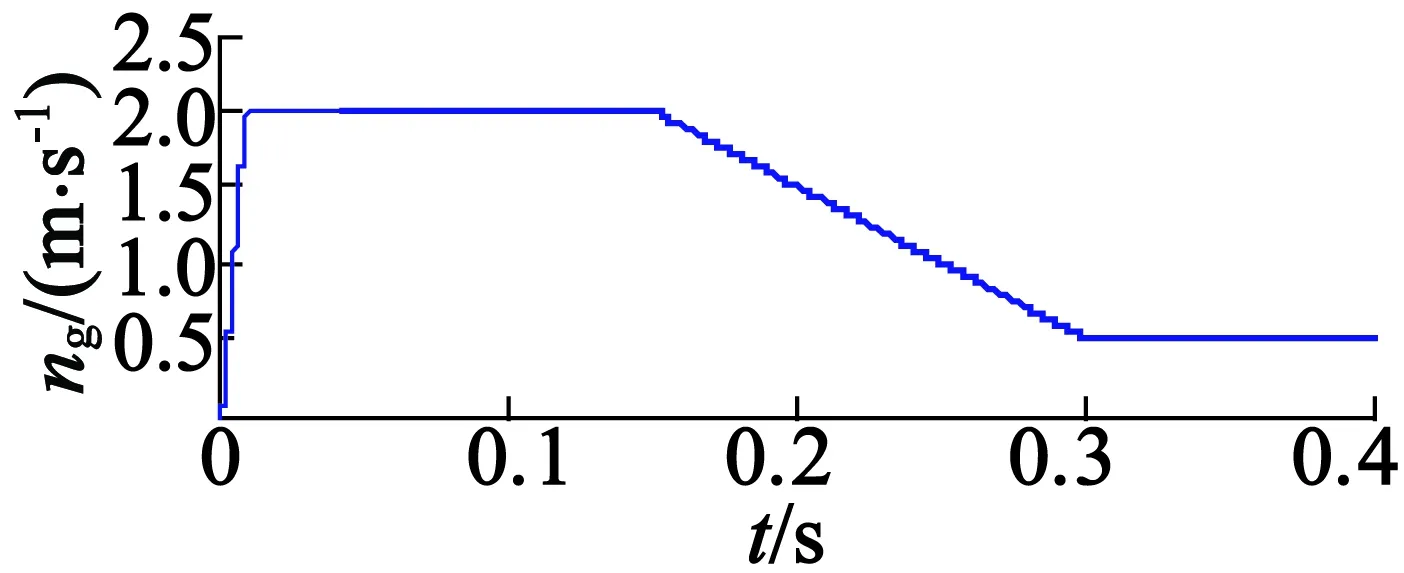

图12 减速给定真实速度、估算速度速度估算误差
为了对无传感器方法进行实验验证,搭建实验平台如图13所示,得到的实验波形包括观测反电势波形,真实和估算位置,真实和估算速度如图14~图16所示,验证了无传感器方法的有效性。

图13 实验平台实物图

图14 观测反电势波形

图15 真实位置,估算位置和位置估算误差

图16 真实速度,估算速度和速度估算误差
4 结 语
本文对初级分段永磁直线同步电机的无传感器控制问题进行了研究,提出段间区域位置和速度估算的方法。由仿真和实验结果可知,该方法有效地消除了段间位置估算存在的盲点,减弱了常规估算方法在段间区域存在的速度波动问题,提高了分段电机位置和速度的估算精度,对于分段电机具有实用性。
[1] 上官璇峰,励庆孚,袁世鹰,等.不连续定子永磁直线同步电动机运行过程分析[J].西安交通大学学报,2004,38(12):1292-1295.
[2] 上官璇峰,励庆孚,袁世鹰.多段初级永磁直线同步电动机驱动系统整体建模和仿真[J].电工技术学报,2006,21(3):52-57.
[3]SUZUKIK,Yong-JaeK,DOHMEKIH.Drivingmethodofpermanent-magnetlinearsynchronousmotorwiththestationarydiscontinuousarmatureforlong-distancetransportationsystem[J].IEEETransactionsonIndustrialElectronics,2012,59(5):2227-2235.
[4]MIHALACHIM,LEIDHOLDR,MUTSCHLERP.Lineardrivesystemforcombinedtransportationandprocessingofmaterials[C]//35thAnnualConferenceofIEEE,2009:1185-1190.
[5]MIHALACHIM,LEIDHOLDR,MUTSCHLERP.Motioncontrolforlongprimarylineardrivesusedinmaterialhandling[C]//2010 14thInternationalPowerElectronicsandMotionControlConference(EPE/PEMC),2010:94-101.
[6]LEIDHOLDR,MUTSCHLERP.Speedsensorlesscontrolofalong-statorlinearsynchronous-motorarrangedbymultiplesections[C]//31stAnnualConferenceofIEEE,2005:1395-1400.
[7]LEIDHOLDR,MUTSCHLERP.Speedsensorlesscontrolofalong-statorlinearsynchronousmotorarrangedinmultiplesegments[J].IEEETransactionsonIndustrialElectronics,2007,54(6):3246-3254.
[8]MIHALACHIM,LEIDHOLDR,MUTSCHLERP.Longprimarylineardriveformaterialhandling[C]//InternationalConferenceonElectricalMachinesandSystems,IEEE,2009:1-6.
[9]LEIDHOLDR,MUTSCHLERP.Sensorlessposition-controlmethodbasedonmagneticsalienciesforaLong-StatorLinearSynchronous-Motor[C]//32ndAnnualConferenceonIndustrialElectronics,IEEE,2006:781-786.
[10] 尚喆,赵荣祥,窦汝振.基于自适应滑模观测器的永磁同步电机无位置传感器控制研究[J].中国电机工程学报,2007,27(3):23-27.
[11] 苏健勇,杨贵杰,李铁才.PMSM扩展状态滑模观测器及转子位置和速度估算[J].电机与控制学报,2008,12(5):524-528.
[12] 鲁文其,胡育文,杜栩杨,等.永磁同步电机新型滑模观测器无传感器矢量控制调速系统[J].中国电机工程学报,2010,30(33):78-83.
[13]YOSHIDAK,TAKAMIH,FUJIIA.Smoothsectioncrossingofcontrolled-repulsivePMLSMvehiclebyDTCmethodbasedonnewconceptoffictitioussection[J].IEEETransactionsonIndustrialElectronics,2004,51(4):821-826.
[14] 李立毅,谭广军,刘家曦,等.基于Luenberger观测器的高速PMSM无传感器技术研究[J].微特电机,2013,41(4):31-34.
[15] 范蟠果,杨耕.感应电机无速度传感器控制自适应速度观测器[J].电机与控制学报,2008,12(6):621-628.
[16] 刘家曦,杨贵杰,李铁才.基于线性磁链的IPMSM位置预估算法[J].哈尔滨工业大学学报,2011,43(6):81-85.

