基于密度控制的多倍高单元详细布局算法

陈秀华

(福建船政交通职业学院 公共教学部，福建 福州 350007)

基于密度控制的多倍高单元详细布局算法

陈秀华

(福建船政交通职业学院 公共教学部，福建 福州 350007)

针对多倍高单元详细布局问题，提出了一种基于密度控制的高效多倍高单元详细布局方法。首先给出一种新的多倍高标准单元密度计算方法，接着提出一种嵌套式动态规划的高效算法用于优化详细布局中的线长和密度2个目标，采用标准的测试例子集进行测试。实验结果表明，文中所提出的算法可以在合理的运行时间里得到很好的详细布局结果。

多倍高单元;详细布局;密度控制;动态规划

0 引言

超大规模集成电路(Very Large Scale Integration，VLSI)设计中的布局一般分为3个阶段：全局布局、合法化布局和详细布局。全局布局一般是基于线长最小化目标来确定每个单元的大概位置，也可以根据布线或时延等目标来确定单元的位置。但全局布局的结果经常是重叠的，需要通过合法化来消除重叠的单元并重新确定单元的位置。详细布局通过局部移动单元位置来优化布局的质量。详细布局是VLSI设计中非常关键的一个环节，对芯片的质量有重大影响。

在当前超大规模集成电路设计中，一直只考虑单倍高的标准单元。随着技术的发展，依据不同的特征，如：时延、封装、引脚可访问性等，各种不同宽度和高度的单元被使用[1]。随着标准单元的高度变得越来越小，为满足布线特征等各种要求，电路元件设计的复杂度也不断增加。此外，为了满足面积、功率和低成本等要求，布局密度经常高达90%，几乎接近极限，详细布局就成了解决局部线路拥堵问题的关键[2]。在一个极其密集的设计中，如果不破坏局部布局，只靠合法化和详细布局插入或移动大的单元几乎是不可能的。此外，在给定的单元库中每个单元的引脚数和面积是不一样的，并且引脚数和面积大小无关，当引脚数大的单元个数过多时就会造成局部拥堵。因此在给定芯片面积的情况下，采用合适的方法同时优化线长和消除拥堵是至关重要的。

吴刚等在文献[3]中首次提出一种技术来处理双倍高单元的详细布局，使用单元分组和单元膨胀将单倍高单元转化成双倍高单元，使得在布局中只有双倍高单元。然而，这种方法无法处理多倍高单元的电源线对齐约束，也不能处理3倍高以上的单元。文献[4]则首次提出了关于位移最小化目标的多倍高合法化算法，考虑了布局中的插入点，并在位移最小化目标下试图消除重叠单元。

1 问题描述及其数学模型

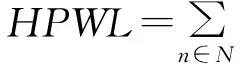
(1)

式(1)中，N表示网表(线网的集合)。

平均格子利用率(ABU)是用来评估布局密度的一种方法。ABUγ表示密度在前γ%的格子的平均值。基于密度的ABU罚定义成overflow的权重和，其方程如下：

(2)

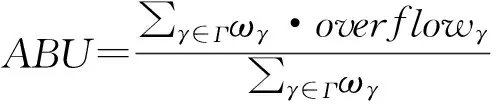
(3)

式(2)～(3)中，dt为目标利用率;ω2,ω5,ω10,ω20设为10，4，2，1。在2013年ICCAD布局竞赛中定义广义的线长包括线长密度花费，如公式(4)：

sHPWL=HPWL(1+ABU)

(4)

其中，计算ABU时只包括单元面积利用率。随着技术的发展，面积利用率已经不是计算拥堵的最佳办法。因为一些大的单元可能包含很少的引脚，而一些小的单元却可能有很多引脚连接、很多线网，所以我们提出平均引脚利用率(APU)来计算布局中的引脚分布。每个单元的引脚密度为引脚数与格子(将布局区域划分成大小相同的格子)位置的比例。一旦获得引脚密度分布，则APU罚的计算跟ABU相同。

多倍高详细布局(MrDP)问题的定义如下：

给定一个初始多倍高标准单元布局和一些固定宏块，不管该布局合不合法，为优化线长和密度而得到的一个合理的、高质量的解决方案，即sHPWL和APU最小。

2 多倍高单元详细布局算法

2.1 算法的整体框架

详细布局算法见表1。对总体布局给定布局的解决方案，首先检查该布局是否合法。如果不合法，则去除重叠执行并使多倍高单元的电源线对齐。在这一步中，首先执行链移动算法(表2)以减少单元重叠，因为初始的解决方案可能包含许多重叠导致合法化难以进行；接下来再利用文献[2]中德尔合法化来确保位移最小；然后同时优化线长和密度直至算法达到最大步或者不超过1%的单元可以移动时终止。在实验中最多允许迭代6次，在最终布局前提出嵌套式动态规划算法(表3)来优化线长。

表1 详细布局算法

表2 链移动算法

表3 嵌套式动态规划算法

2.2 链移动算法

详细布局通常是通过cell-by-cell manner 方法来优化线长，即一个单元试图与另一个单元交换或移到更好的位置，从而得到更好的线长[6-8]，该方法对单倍高详细布局十分有效。多倍高单元因占据多个行，会使更多的单元产生重叠，如果仍用此方法将导致布局失败。如果没有扰动，则至少2个单元很难再插入另一个多行高度单元，类似的情况也会发生在其他大的单元上。根据文献[9]密度的重新定义和文献[10-11]中获得的映射形式，采用允许其他单元同时移动以优化单个目标单元的策略,具体算法框架见表2。

2.3 嵌套式最短路径问题

有序多倍高布局问题通常将转化成有上下限的嵌入式最短路径问题，然后采用嵌入式动态规划算法来解决。定义最大位移量为M，则每个单元的位移值为K=2M+1。令Zij表示分裂单元Zi在第j位置；r表示在Rdr上分裂单元的个数；b表示在Rdr上行单元的个数；t表示在Rdr下行单元的个数。

有序多倍高单元布局问题中一个关键点在于：对于每个划分即子问题都是独立的，所以分裂单元的位置可以被固定下来。例如，在单元e 的位置固定下来后，划分的单元就变得独立了。如果可以固定分裂单元的位置，那么原问题就可以分解成一个个子问题。因此，将原问题转化成了嵌入式最短路径问题，其中outer-level 问题(求最短路径问题)是为了求出分裂单元的位置，inner-level是关于边的权重问题。

outer-level 最短路径算法中每个节点表示分裂单元的候选位置，本算法需要求从s到t的最短路径。在预先知道独立的性质下，可以通过求解inner-level问题计算出各边的权重。由于没有横跨矩形区域的单元，所以这2个问题相互独立。

2.4 嵌套式动态规划算法

关于优化线长和合法化的有序单倍高布局已得到较为广泛的研究[12-16]，本文采用嵌套式动态规划的算法来有效解决多倍高单元详细布局问题。表3给出了嵌套式动态规划算法的框架。通过SolveOuterLevel 函数求outer-level问题，SolveOuterLevel的核心程序是7～15行中的3个循环。每个候选位置的花费通过ComputeDPCost函数来计算。通过SolveInnerLevel函数来求解每个划分的inner-level 花费问题。在每个划分里，利用SolveInnerLevel里面的ComputeDPCost函数分别计算上下行的花费。由于inner-level 问题在理想情况下与单倍高问题相同，本文省略其中的细节。

ComputeDPCost的线长花费采用文献[5]中定义单倍高布局的花费函数计算。如果单元Ci与单元Cj在同一行，并且Cj在Ci的左边，那么假设Cj在这一行最左边的位置，并计算此时的线长花费。如果单元Ci与单元Cj在同一行，并且Cj在Ci的右边，那么假设Cj在这一行最右边的位置，并计算此时的线长花费。如果单元Ci与单元Cj不在同一行，就按它们所在的真实位置计算。这样的计算结果与单倍高布局里的HPWL等价，也与理想情况下的双倍高布局相同。

算法3的运行时间复杂度为O(M2n)，其中n表示在矩形区域里的单元的个数。考虑被r个单元划分成r+1个块，在每个块(划分)中，下行有bi个单元，上行有ti个单元。假设ComputeDPCost只需时间为常数且n远大于r。文献[17]中用来解决单倍高布局的动态规划算法只需要O(Mn)的时间复杂度。所以在SolveInnerLevel中对每个划分的计算需要O(Mbi)+O(Mti)的时间复杂度。算法3的时间复杂度为：

(5)

本文提出线长、单元密度、引脚密度的多倍高详细布局算法，主要贡献为：

1)为优化线长、单元密度、引脚密度，提出关于多倍高的链移动方法。

2)采用嵌套式动态规划高效解决有序的多倍高线长优化布局。

3)本文方法与最新的详细布局相比能提高3%的线长规模，在单元密度上提高了13.2%，在引脚密度上提高了13.3%。

3 实验结果

本文算法在主频3.4 GHz、内存32 G的Linux操作系统下用C++实现，采用文献[1]提供的ISPD05 placement benchmark测试数据(表4)进行仿真实验和验证，在HPWL、sHPWL、CPU等方面与文献[1]算法进行对比，算法实验结果比较见表5。

表4 ISPD05测试数据集[1]

表5 算法实验结果比较

在合理的运行时间内，本文所提出的算法在HPWL、sHPWL、ABU的罚和APU的罚等方面比文献[1]算法的结果均有明显提高。对于表4中的所有实例，在HPWL方面，本文算法都比文献[1]算法明显缩短，平均缩短了1.2%；在sHPWL方面，平均缩短了3.0%; ABU的罚比文献[1]平均减少了13.3%；APU的罚比文献[1]平均减少了13.2%。由此说明本文算法可获得更好的单元格密度，得到较好的详细布局结果。

4 结束语

本文提出了基于密度控制的高效多倍高单元详细布局方法,将基于嵌套式动态规划的高效算法用于优化详细布局中的线长和密度2个目标,采用标准的测试例子集进行测试。实验结果表明本文所提出的算法可以在合理的运行时间里，得到很好的详细布局结果。

[1] 徐宁，洪先龙.超大规模集成电路物理设计理论与算法[M].北京：清华大学出版社，2009:4-6.

[2] 南国芳.VLSI物理设计中关键问题求解的算法研究[D].天津：天津大学，2004.

[3] Wu G,Chu C.Detailed placement algorithm for VLSI design with double-row height standard cells[J].IEEE Trans.on CAD of Integrated Circuits and Systems,2016,35 (9):1569-1573.

[4] Chow WK,Pui CW,Young EFY.Legalization algorithm for multiple-row height standard cell design[C]//Design Automation Conference,Las Vegas,Nevada:IEEE Design Automation,2016:1-6.

[5] Kim MC，Viswanathan N,Li Z,et al.ICCAD-2013 CAD contest in placement finishing and benchmark suite[C]//International Conference on Computer-aided Design,San Jose,CA:IEEE Computer Society,2013:268-270.

[6] Chow WK,Kuang J,He X,et al.Cell density-driven detailed placement with displacement constraint[C]//International Symposium on Physical Design,Petaluma,CA:ISPD,2014:3-10.

[7] Pan M,Viswanathan N,Chu C.An efficient and effective detailed placement algorithm[C]// International Conference on Computer-aided Design,San Jose,CA:IEEE Press,2005:48-55.

[8] Popovych S,Lai HH,Wang CM,et al.Density-aware detailed placement with instant legalization[C]//Design Automation Conference,Las Vegas,Nevada:IEEE Design Automation,2014,42(2):1-6.

[9] Lin T,Chu C,Shinnerl JR,et al.POLAR:placement based on novel rough legalization and refinement[C]//International Conference on Computer-aided Design,San Jose,CA:IEEE Computer Society,2013,21(1):357-362.

[10] Kernighan BW,Lin S.An efficient heuristic procedure for partitioning graphs[J].Bell System Technical Journal,1970,49(2):291-307.

[11] Fiduccia CM,Mattheyeyes RM.A linear-time heuristic for improving network partitions[C]//Design Automation Conference,Las Vegas,Nevada:IEEE Design Automation,1982,13(5):175-181.

[12] Brenner U,Vygen J.Faster optimal single-row placement with fixed ordering[C]//Design Automation & Test in Europe Conference,2000:117-121.

[13] Taghavi T,Alpert C,Huber A,et al.New placement prediction and mitigation techniques for local routing congestion[C]//International Conference on Computer-aided Design,San Jose,CA:IEEE Press Piscataway,2010:621-624.

[14] Kahng AB,Tucker P,Zelikovsky A.Optimization of linear placements for wirelength minimization with free sites[C]//Asia and South Pacific Design Automation Conference,San Jose,CA:IEEE Press,1999:241-244.

[15] 李康.VLSI物理设计中布局及有约束的布局优化[D].成都：电子科技大学,2010.

[16] 高文超，周强，钱旭,等.应用于大规模集成电路非线性布局的二元结群算法[J].计算机辅助设计与图形学学报，2013，25(7)：1083-1088．

[17] Lin Y,Yu B,Zou Y,et al.Stitch aware detailed placement for multiple e-beam lithography[C]//Asia and South Pacific Design Automation Conference,San Jose,CA:IEEE Press,2016:186-191.

(责任编辑 吴鸿霞)

An Efficient Algorithm for Multiple-row Detailed Placement Based on Density Control

ChenXiuhua

(Department of Basic Courses，Fujian Chuanzheng Communications College，Fuzhou Fujian 350007 )

This paper proposed an efficient algorithm for multiple-row detailed placement based on density control.Firstly,a new algorithm for multiple-row height standard cell density was given,then an efficient algorithm with a nesting dynamic programming was used to optimize the line length and density of the detailed placement,the test was done by the ISPD05 placement benchmark suite.Experimental results showed that the proposed algorithm can achieve the best result of detailed placement in the reasonable running time.

multiple-row height cell;detailed placement;density control;dynamic programming

2017-01-16

福建省教育厅科技项目(项目编号：JA10284;JB07283)；福建省交通科技发展项目(项目编号：201011)。

陈秀华，副教授，硕士，研究方向：图论及其应用、优化理论与算法。

10.3969/j.issn.2095-4565.2017.02.010

O157.6

A

2095-4565(2017)02-0045-05