我国海工装备制造业上市公司效率评价研究

王 奇， 纪建悦

（中国海洋大学 经济学院，山东 青岛 266100）

引 言

海洋工程装备制造业是一种为海洋资源的开发及海洋产业的发展提供必要基础设施的产业，它属于高投入、高产出、高风险、高附加值的技术导向型的产业。当前，海洋资源、空间争夺日益激烈，海工装备制造业已逐渐成为各沿海国家及地区的战略性支柱产业[1]。

2009年，国家工信部制定的《船舶工业调整和振兴规划》，将“发展海洋工程装备”列为我国先进制造业发展的主要任务之一。同年，我国制定的《海洋工程装备科研项目指南（第一批）》确定了我国海洋工程装备发展的目标以及研发重点。2010年国务院颁布了《关于加快培育和发展战略性新兴产业的决定》，将海洋工程装备作为高端装备制造业的重要组成部分，并且明确提出了“面向海洋资源开发，大力发展海洋工程装备”，这一决定将海洋工程装备制造业列为国家战略重点支持发展对象，也推动着我国海洋工程装备制造业的发展。

随着我国“建设海洋强国”战略的不断深入，我国已在“珠三角”“长三角”以及环渤海地区形成了具有相当规模的海工装备产业集聚区，涌现了一批实力突出、竞争力强的企业。但是，中国的海洋工程装备制造业与世界先进水平相比，仍存在着一定的差距[2]。据有关数据统计，2015年中国海工装备制造业订单总额为38.2亿美元，同比减少75.5%。现阶段，我国船舶工业发展中仍然存在着许多问题：结构性产能过剩突出，高端产能不足，低端产能过剩，管理水平差距较大，效率亟待提高。在这种背景下，对我国的海洋工程装备制造的效率问题进行研究是十分必要的。

目前对于海洋工程装备制造业的研究，国外主要是见于一些产业发展报告形式。《新加坡海洋装备制造业行业研究报告》在较全面的分析海洋装备市场前景的基础上，分析新加坡重点海洋装备企业的发展所面临的环境，同时提出了新加坡在未来的海工装备的发展方向；韩国海洋装备研究所发表的《A Global Leader in Marine Equipment Research&Testing》[3]回顾了韩国海洋装备业发展的历史进程，并对海工装备产业体系的构建和运行等进行相关分析。在国内关于海洋工程装备制造业的研究主要是进行定性的分析。赵阳华[4]分析了我国海工装备制造业的发展现状并提出相关对策建议；刘全等[5]认为随着陆地资源日趋枯竭，人类生存和发展将越来越多地依赖海洋，并分析了我国海工装备业现状及发展趋势；陶永宏、陈勇[6]采用SWOT分析方法探讨我国海工装备业发展面临的内、外部环境，并提出海工装备发展的战略选择。由此可见，当前对我国海洋工程装备制造业的效率评价文献比较少。鉴于此，本文拟以我国海工装备制造业的上市公司为样本，对其经营效率进行实证研究。

1 效率评价模型的引入

对效率的评价常用的有参数方法和非参数方法，非参数方法以DEA为代表，由于非参数方法不需要考虑具体的生产函数形式及参数的分布状况，所以在效率评价中应用较多。传统的一阶段DEA有明显的缺陷，它是将所有的投入变量、产出变量以及相应的环境变量等全部纳入到规划中，估算出生产前沿边界和各决策单元效率，这一方法的主要问题在于，将环境变量统一进行规划，会使得各个决策单元可能出现异质性，从而造成所求得的效率值将会存在偏差。两阶段DEA方法，也就是在传统的一阶段DEA中引入了Tobit回归进行分析；这一方法可以分析出对效率造成影响的各因素显著水平，但是其本质上并没有剔除掉环境和随机误差对效率值造成的影响，得到的效率也并不能精确反映各个决策单元真实管理效率，因此二阶段DEA效率评价方法也是有偏的。为此Fried等[7]提出的三阶段DEA方法，也是目前对效率评价常用的方法。该方法最大的优势是能够有效的剔除外部环境因素以及包含于冗余变量中随机误差对决策单元效率的影响，进而得到的效率值能够更加真实可靠地反映实际。

利用三阶段DEA方法来评估效率的文献有很多。郭军华等[8]运用三阶段DEA（数据包络模型）对我国2008年的农业生产效率进行了实证研究；白俊红，蒋伏心[9]应用三阶段DEA方法，在控制环境因素的基础上考察了我国区域创新的效率问题；蒋萍等[10]应用三阶段DEA和超效率DEA模型对我国31个省份2008年文化产业投入产出效率进行了分析；Jonchi Shyu等[11]采用三阶段DEA方法对台湾的各银行分支机构的管理效率进行研究分析；郭亚军[12]运用三阶段DEA模型对我国2009年工业生产效率进行实证研究；华坚等[13]基于三阶段DEA的方法，评级了中国省际区域二氧化碳排放绩效；刘伟等[14]将三阶段DEA模型与Bootstrap方法相结合，在控制环境因素影响的基础上测算了中国省际高新技术产业的技术创新效率；任毅，丁黄艳等[15]通过三阶段DEA方法，主要从外部环境、省际差异和效率结构等方面对“十五”到“十二五”期间长江区域经济带工业能源效率空间差异化和发展趋势进行实证研究。

上述三阶段DEA模型能够剥离外部环境和随机误差的影响，但是在第二阶段构建SFA模型中，对于环境变量的选取存在人为因素的干扰，并且对最优的生产前沿面缺乏稳健性检验，因此，本文主要是运用杨力、王舒鸿[16]所采用的三阶段DEA方法，不仅可以消除环境因素和随机误差的影响，而且可以对有效前沿面进行稳健性检验从而剔除异常决策单元，以便对前沿面的决策单元进行重新排序和效率评价。

1.1 DEA初始阶段评价

数据包络分析是A Charnes等[17]于1978年提出的一种非参数效率评价方法，该方法是根据决策单元（Decision Making Unit，简记DMU）的投入产出数据，利用线性规划来包络出一个最佳的生产前沿面，根据每个DMU与生产前沿面的距离来确定他们的相对效率值。数据包络分析适用于对具有多指标投入与多指标产出特点的相同类型单元的相对效率进行评价，不需要任何变量之间的函数假设，也不必人为的确定决策单元的权重，避免了很多主观因素的影响。其基本的模型有CCR模型和BCC模型[18]。本文采用CCR模型。

CCR模型是以规模报酬不变为假设，采用线性规划来估计决策单元的生产前沿面，评价每一个决策单元的相对效率。

设有n个决策单元，每个决策单元有m种输入和s种输出，效率评价公式为：

式中：Xj和Yj分别为决策变量的投入和产出向量，μT和ωT分别为权重变量，利用对偶原理引入了松弛变量S-和剩余变量S+后，可得：

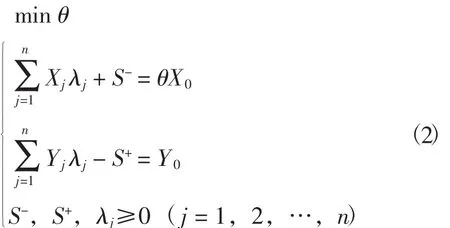
其经济意义是：

①θ=1且S+=S-=0时，称DMU为DEA有效，此时决策单元DMU同时为技术有效和规模有效；

②θ=1且S+=S-＞0时，称DMU为弱DEA有效，此时决策单元DMU不同时技术有效和规模有效；

③θ＜1，称DMU是无效的，此时决策单元既不技术有效也不规模有效；

④如果存在λj（j=1，2，…，n），有则该决策单元的规模效益不变；如果则该决策单元的规模效益递减，如果则该决策单元的规模效益递增。

1.2 DEA有效决策单元的二阶段评价

通过第一阶段的效率评价，可以确定一个由所有决策单元所形成的生产前沿面，但是这一结果并不能分离随机变量和测量误差的影响，同时决策单元的效率会受到投入和产出变量选择的影响。因此，在进行第二阶段的效率评价前，有必要进行稳健性检验。本文引入Jackknifing检验法，从而剔除在生产前沿面上的异常决策单元，使得最优前沿面上的决策单元具有同质性。借助于多目标决策的TOPSIS方法中的相关理论，引入了最优虚拟决策变量，即最少投入最多产出的决策单元，对经过稳健性检验后的有效前沿面上的决策单元进行重新评价和排序。

1.3 DEA有效决策单元的三阶段评价

通过第二阶段的DEA评价，可以得到在前沿面上管理效率相对较高的决策单元，并以此作为参照，对前沿面上的其他决策单元进行标准化处理，然后根据修正后的效率值，对各决策单元的投入冗余和产出不足进行约束，从而实现对无效决策单元调整的目的，最后将这些修正的决策单元进行规划和评价，即三阶段的DEA评价。

2 我国海工装备制造业上市公司的实证分析

2.1 数据的选取

本文选取了我国海高装备制造业上市公司的资产负债表和利润表，以2015年12月31日的数据为研究样本，对18家上市公司进行DEA综合经营效率分析。

从资产负债表和利润表中选取投入和产出变量，根据经验，所选取的指标总数不能超过决策单元的二分之一，也就是说，对18家企业进行分析，则投入和产出的指标数不能超过9个，否则会导致评价的无效。本文在选取指标时充分考虑到滞后因素和长期因素，选取时点指标；如果选取的指标具有滞后性，那么在进行DEA评价时，就会影响该企业在包络面上的位置，使得效率评价不够准确。依据这个原则，在资产负债表中，考虑到货币资金是一种流动性较强的一项指标，因此将其单独作为投入变量；长期股权投资是指通过投资取得被投资单位的股份，对衡量企业的投入具有重要的价值；固定资产净额反映了企业的账面价值情况；非流动资产合计也是衡量企业运行的重要因素，被作为投入要素。在利润表中，营业收入是衡量企业收入的重要部分，营业利润、利润总额以及净利润是企业投资者和企业参与管理者最重要的参考指标，因此作为产出指标。综上，对于投入指标，选取了货币资金、长期股权投资、固定资产净额、非流动资产合计；对于输出指标，选取了营业收入、营业利润、利润总额以及净利润（见表1）。

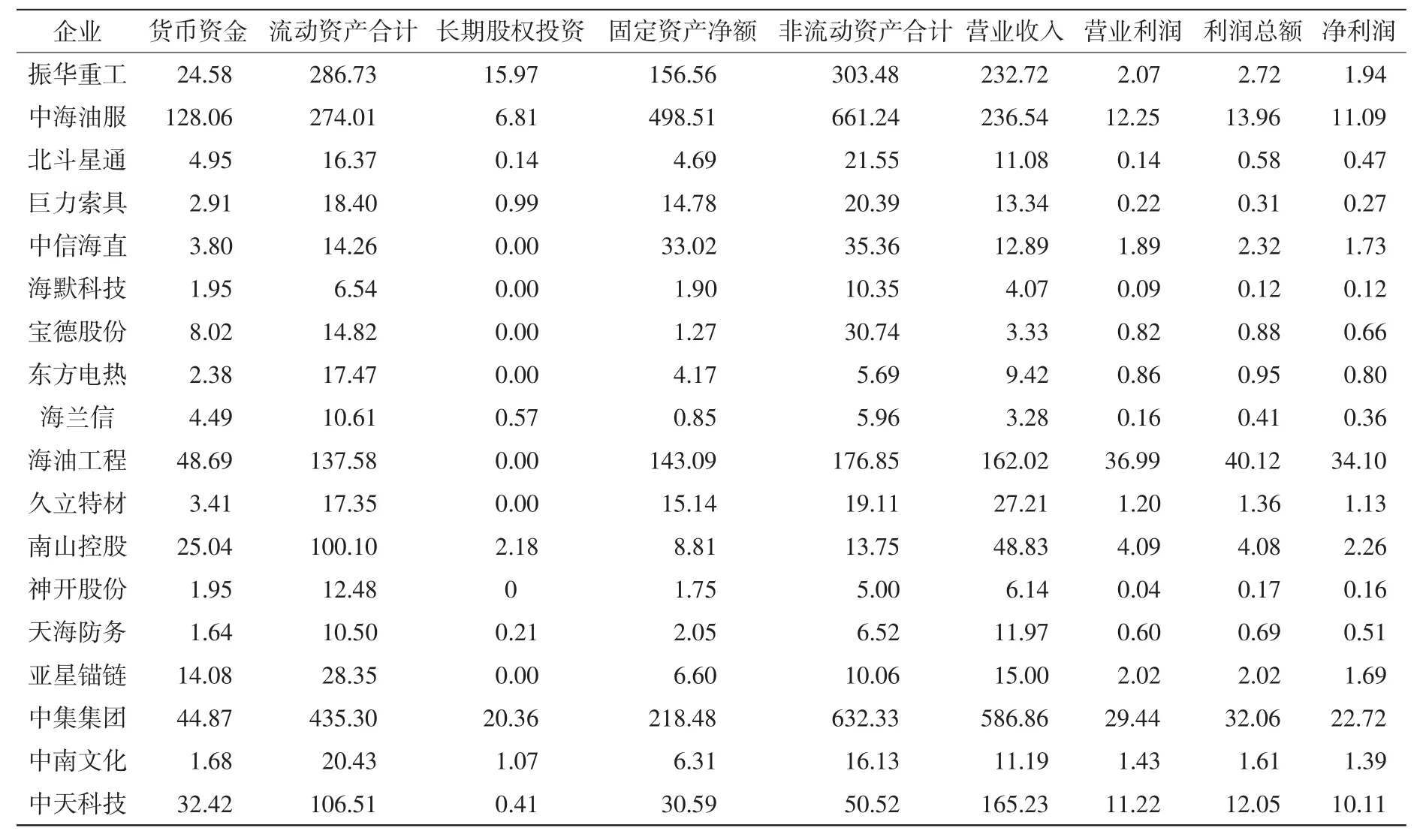
表1 18家上市公司的各项原始财务指标Tab.1 Raw financial indicators of 18 listed companies

2.2 决策单元的初始阶段评价

利用Maxdea软件分析，以投入导向型的CCR模型得到了各决策单元的效率得分和投入冗余的结果（见表2）以及产出不足结果（见表3），表中未列出到达帕累托最优的12家企业，其效率值是1，投入冗余和产出不足均为0。

从表2和表3可以看出18家上市公司中在初次DEA评价后，有12家企业的效率值为1，达到了帕累托最优或者弱帕累托最优，构成了最优效率前沿面。在无效率的6家企业中，其中最高的是海默科技，为0.873 5，而北斗星通的效率值最低，为0.437 9，足以看出我国海工装备制造业企业的发展参差不齐。

表2 决策单元的得分和投入冗余的结果Tab.2 Decision-making unit′s score and results of redundant input

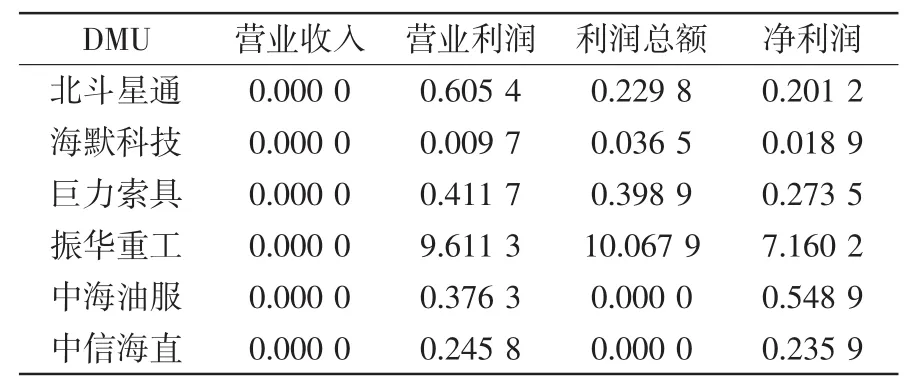
表3 产出不足的结果Tab.3 The result of insufficient output

2.3 DEA有效决策单元的第二阶段评价

有很多因素都会影响DEA结果的稳定性。尽管有12家企业已经达到了效率值为1，即处在最优的生产前沿面上，但DEA效率是相对效率，这12家企业哪家更好，或者说是否存在这样一家企业比较孤立，从整体上会大幅度地改变生产前沿面的形状，从而严重影响了评价的真实客观性。所以，应在初次DEA评价之后，进行效率评价的稳健性检验，本文引入Jackknifing检验法，其原理是将已经达到效率最优的决策单元剔除，然后再对剩余的决策单元进行评价，如果最终得到的效率值和初次得到的效率值相差不大，那么这个这个决策单元不是异常值，则继续剔除其他的决策单元，按照这个方法得到了剔除后的效率评价值（见表4），其中，由于原先在生产前沿面的决策单元在二次DEA评价后依然在生产前沿面上，所以表中不在列出；在表中的左侧是剔除的决策单元，上方是无效率的6家企业。

为了更加直观的量化异常指标的异常性，本文对上述的各个效率值之间进行相关性检测，结果见表5。

从表5中可以看出相关性系数大部分在92%以上，只有去掉中天科技时产生的波动，相关性系数在76.60%左右，因此可以判断出中天科技是异常值，应该予以剔除，才能使得评价更加具有客观性，此时剔除后的效率值如表4中最后一行所示，北斗星通和中海油服这两家家公司的效率值均有所提高。

表4 Jackknifing检验法得出的效率评价值Tab.4 The efficiency evaluation value obtained by the Jackknifing test

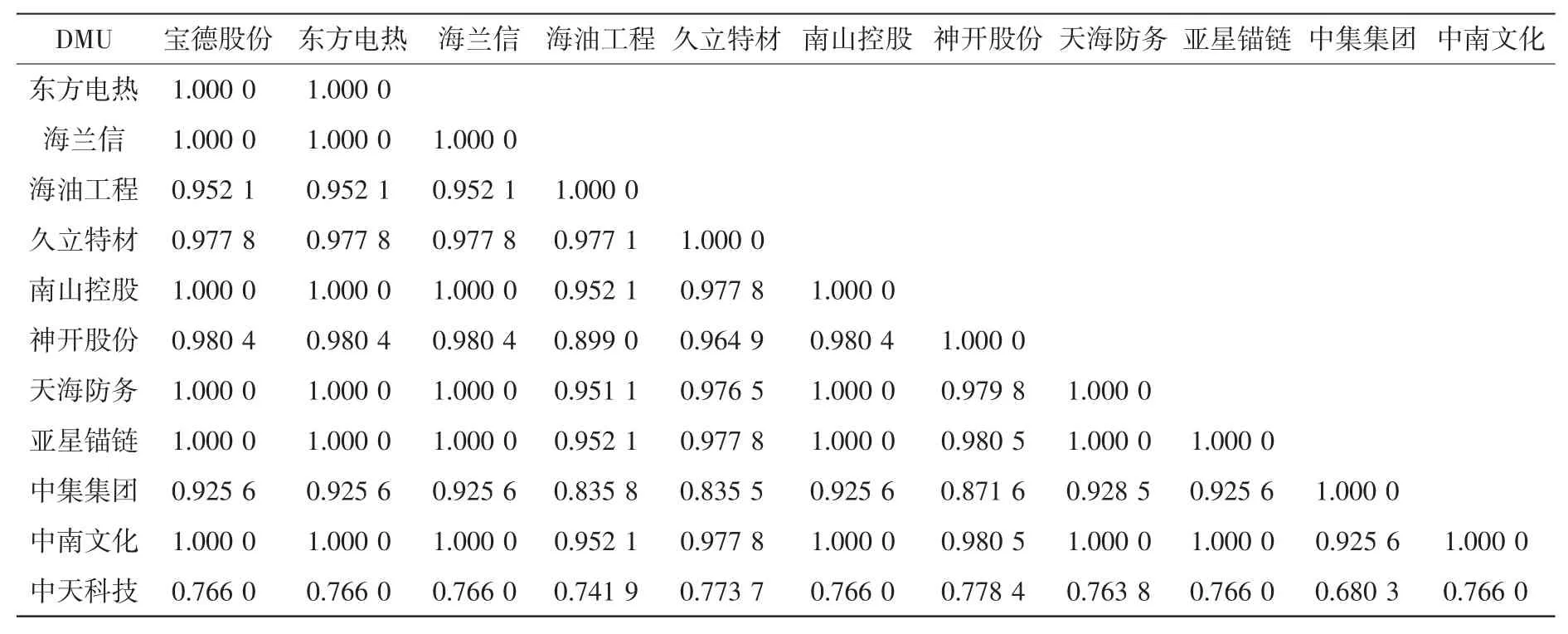
表5 相关性系数Tab.5 The correlation coefficient

上述把中天科技这一异常值剔除后，进行DEA的二阶段评价中，剩余的11家企业的相对有效性仍然具有差异性，于是在此引入最佳的虚拟决策变量，再进行二次评价。本文借鉴多目标决策方法TOPSIS中有关构造理想的虚拟决策变量的做法，选取每一个输入中的最小值作为这一理想决策变量的初始投入量，每一个产出中的最大值作为这一理想决策变量的初始产出量，来构造一个新的优势前沿面，尽管在现实中，构建的虚拟理想决策单元不一定会实现，但是其效率值为1，使得其他11家企业就变得相对无效率，以此实现对11家企业的重新排序。

由于剔除了中天科技这一决策变量，导致了决策单元数的减少，如果再继续使用原来的投入产出指标，那么DEA评价结果就会出现不稳定的情况，因此，需要进一步减少投入和产出指标。一般来说，减少指标的方法主要有主成分分析、因子分析和AHP决策方法等，本文选取的是财务数据，在分析的模型中，只考虑总量指标，那么投入指标选择的是流动资产合计、长期股权投资和固定资产净额这三个指标，产出指标选择的是营业收入和利润总额这两个指标。将11家企业和构造的最优虚拟决策变量进行DEA的二次评价，结果见表6。

从表6中可以看出，经过二阶段评价后，海油工程的效率值最高，为0.076 3；而神开股份的效率值最低，为0.008 8。那么，为了获知对这几家企业如何进行有效的管理，进行三阶段效率评价。

2.4 DEA有效决策单元的第三阶段评价

在得到二阶段评价效率值后添加一个虚拟决策变量，是为了对这11家企业进行重新排序，进而在这11家企业中找到一个相对来说最有效的企业，首先将上述最优虚拟决策单元去掉，可以知道海油工程的效率值是相对最高的。

令 θ1，θ2，…，θ11为这 11 家企业的效率值，θi是这11家企业的效率值最大值，即θi=max（θ1，θ2，…，θ11），以效率值最大值对其他企业的效率进行标准化，即令：

表6 二阶段评价后各企业的投入冗余值和产出不足值Tab.6 After the evaluation of the two stages， the enterprises′input redundancy and output deficiency are evaluated

图1 11家企业修正后的效率值Fig.1 The efficiency values of the 11 enterprises

经过标准化后，第i个决策单元的效率值为1，其他的决策单元均小于或等于1，11家企业的效率值如图1所示。

根据规划，模型如下：

式中：θ*i是修正后的效率评价值，利用修正的效率值对模型中的投入和产出值进行重新规划，对投入冗余和产出不足进行约束，以达到对无效率决策单元调整的目的。

根据上述模型，得到11家企业中无效率企业的效率值和投入冗余、产出不足值（见表7）。

表7中未列示效率值达到1的企业，只列出了未达到帕累托最优的六家企业，分别为：海兰信，久立特材，南山控股，天海防务，中集集团和中南文化。对于海兰信企业，如果长期股权投资减少0.048 7亿元并且利润总额增加0.000 4亿元时，该企业的经营效率就会大大增加，生产阶段不断向帕累托最优效率状态演进。同理，久立特材，南山控股，天海防务，中集集团和中南文化也应按着上述的规划进行，以达到帕累托最优状态。

表7 三阶段评价的投入冗余值和产出不足值Tab.7 Redundant and insufficient values for the three-stage evaluation

3 提高我国海工装备制造业效率的相关建议

通过实证分析可以发现：得出的结果比较贴近当前我国海洋工程装备制造业发展现状，引入基于DEA的三阶段效率评价模型对我国海洋工程装备制造业进行效率评价与分析也非常有必要。因此，结合我国海洋工程装备制造业的特点，从海洋工程装备制造业相关上市公司这一微观视角出发，提出以下几点相关的建议。

首先，公司应当提高和优化管理水平，注重对企业运营效率的量化评价。在本文的三阶段效率评价结果中发现，尽管部分企业的效率已经相对较高，但是相对于海油工程这一企业仍然存在着一定的进步空间。这就意味着，企业在发展过程中，应该合理吸取其他优势企业在发展和管理中的经验，具备长远发展的眼光，从而更好地促进自身的发展。此外，在企业管理过程中，借助相关的数据和模型，定期对企业效率进行定量评价是非常有必要的，以发现企业在发展过程中所存在的漏洞和不足，对自身发展状况有比较合理的认识和判断，从而更有利于企业的长远发展。

其次，应适当提高对企业发展的扶持力度，加大政策支持，促进各企业间平衡发展。正如本文研究结果所得，我国海洋工程装备制造业的相关企业之间发展水平不平衡，国家应当对相关的企业加大扶持力度，促进各企业提高其核心竞争力，从而带动我国海工装备制造业平衡、稳定、整体发展。

最后，努力提高海洋工程装备制造业企业的产出效率和企业运营效率。从第一阶段DEA效率评价中，可以发现未处在最优前沿面的企业的投入冗余量相对较高，其中部分企业如中海油服这一企业的投入冗余值相对最高，这就要求企业需要提高产出效率。首先应当强化海洋技术研发投入，提高海洋技术核心创新能力，加速科技转换效率，同时加大高素质科研人才的培养和相应资金投入；再次，需要加强对外合作与交流，积极引进国外先进技术和高端人才，支持重点企业开拓海外市场，进行国际战略投资，从而提高企业产出效率；最后，作为企业的管理层应当将视角放长远，决策的制定和执行上应合理高效，吸取优势企业的管理经验，努力提高企业的运营效率，从而促进海工装备制造业的效率提升，稳定发展。

4结语

本文以18家海工装备上市公司为研究样本，采用三阶段DEA对其进行效率评价。首先利用DEA中规模报酬不变投入导向型的CCR模型计算这18家上市公司的效率值，得出12家企业处在生产前沿面上，并利用MAXdea软件得出了每一家企业的投入冗余值和产出不足值，发现这18家企业的投入冗余值和产出不足值之间存在着很大的差距，再加上DEA所得到的效率值是相对效率值，因此，本文认为，在生产前沿面上应该存在某一家或者某几家企业处在异常状态，也就是这一异常企业会使得生产前沿面的形状发生大幅度的变动，为了剔除异常值，引入Jackknifing方法对每一决策变量进行稳健性检验，为了更加直观地发现异常值，对Jackknifing检验得出的效率值又进一步进行相关性检验，得出相关性系数表；通过相关性系数表的分析，发现只有当剔除中天科技时，其他几家企业的效率值才会发生明显的变动，所以中天科技是异常值。

在进行DEA二次评价过程中，为了找到其他11家企业的上升空间，本文借助于多目标决策的TOPSIS方法中的相关理论，引入了最佳虚拟决策变量，这一虚拟决策处在新的最优生产前沿面上，可以利用这一虚拟决策单元对其他11家企业进行全排序，得到每一家企业的进步上升空间，也就是说明企业在发展过程中不能只是单独拘泥于眼前，应该有长远的规划，借鉴其他企业的经验，使得自身处在上升阶段。

通过二阶段DEA效率评价后，得出海油工程的效率值相对最高，并以此作为最优决策单元，对其他的决策单元的投入冗余和产出不足进行修正规划，然后为了得到其他企业在经营过程中的上升路径，参照着中远航运的经营模式，引入了三阶段DEA的效率评价；从三阶段DEA效率评价的结果来看，不仅可以对每一个决策单元进行有效性的排序，还可以获得以某个最优企业为参照，每一个企业在经营中的有效的经营管理决策，可以在一定程度上克服传统的DEA评价方法的不足；同时从本文的研究可以看出，海兰信，久立特材，南山控股，天海防务，中集集团和中南文化这6家海工装备制造企业经过三阶段DEA效率评价后的效率值最高的为0.776 3，而最低的是0.511 9，这也说明了目前我国海工装备制造业中的各相关的企业发展水平很不平衡，而这种不平衡性对我国发展海洋经济的发展势必造成阻碍。

参考文献：

[1]杜利楠，栾维新，片峰.沿海省区发展海工装备制造业的潜力评价研究[J].科技管理研究，2015（9）：66-70.

[2] 赵金楼，徐鑫亮.中国海洋工程装备制造业发展问题研究[J].学习与探究，2014（4）：110-112.

[3] Korea Marine Equipment Research Institute.A Global Leader in Marine Equipment Research&testing[R].Busan:KMERI，2012.

[4] 赵阳华.培育高端装备制造产业的对策研究 [J].中国经贸导刊，2011（3）：16-18.

[5]刘全，黄炳星，王红湘.海洋工程装备产业现状发展分析[J].中国水运，2011（3）：37-39.

[6] 陶永宏，陈勇.基于SWOT分析的我国海洋工程装备业发展战略思考[J].江苏科技大学学报，2010（3）：7

[7] H O Fried ，C A K Lovell，S S Schmidt，etc.Accounting for Environmental Effects and Statistical Noise in Data Envelopment Analysis[J].Journal of Productivity Analysis，2002，17（1-2）：157-174.

[8] 郭军华，倪明，李帮义.基于三阶段DEA模型的农业生产效率研究[J].数量经济技术经济研究，2010（12）：27-38.

[9]白俊红，蒋伏心.考虑环境因素的区域创新效率研究——基于三阶段DEA方法 [J].Finance&Trade Economics，2011（11）：104-136.

[10]蒋萍，王勇.全口径中国文化产业投入产出效率研究——基于三阶段DEA模型和超效率DEA模型的分析[J].数量经济技术经济研究，2011（12）：69-81.

[11]Jonchi Shyu，Terri Chiang.Measuring the true managerial efficiency of bank branches in Taiwan:A three-stage DEA analysis[J].Expert Systems with Applications，2012（39）：11494-11502.

[12]郭亚军.基于三阶段DEA模型的工业生产效率研究[J].科研管理，2012（11）：16-23.

[13]华坚，任俊，徐敏，等.基于三阶段DEA的中国区域二氧化碳排放绩效评价研究 [J].资源科学，2013（7）：1447-1454.

[14]刘伟，李星星.中国高新技术产业技术创新效率的区域差异分析——基于三阶段DEA模型与Bootstrap方法[J].财经问题研究，2013（8）：20-28.

[15]任毅，丁黄艳，任雪.长江经济带工业能源效率空间差异化特征与发展趋势——基于三阶段DEA模型的实证研究[J].经济问题探讨，2016（3）：93-100.

[16]杨力，王舒鸿.基于DEA的煤炭上市公司效率三阶段评价[J].经济管理，2010（4）：147-152.

[17]Charnes A，Cooper W W，Rhode E.Measuring the efficiency of decision making units[J].European Journal of Operational Research，1978，6（2）：429-444.

[18]魏权龄.数据包络分析[M].北京:科学出版社，2004.