寿命服从两参数对数Laplace分布的统计分析方法研究
徐晓岭, 顾蓓青,王蓉华
(1.上海对外经贸大学 统计与信息学院,上海 201620; 2.上海师范大学 数理学院,上海 200234)
【基础理论与应用研究】
寿命服从两参数对数Laplace分布的统计分析方法研究
徐晓岭1, 顾蓓青1,王蓉华2
(1.上海对外经贸大学 统计与信息学院,上海 201620; 2.上海师范大学 数理学院,上海 200234)
首先提出了一种新的寿命分布——两参数对数Laplace分布,研究该分布的密度函数、失效率函数的图像特征以及数字特征,其次在全样本、定数截尾样本以及缺失数据场合下,分别研究了位置参数、刻度参数的点估计与区间估计问题,为满足实际工作者的需要,列出了与枢轴量对应的分位数表,最后通过一个实例说明方法的应用。
两参数对数Laplace分布;全样本;定数截尾样本;缺失数据;点估计;区间估计
称某产品的寿命T服从两参数对数Laplace分布LNL(μ,β),记为T~LNL(μ,β),其分布函数FT(t)和密度函数fT(t)分别为
其中,-∞<μ<+∞称为位置参数, β>0称为刻度参数。
若令X=lnT,则X服从位置参数μ、刻度参数β的两参数对称Laplace分布,记为X~L(μ,β),其分布函数FX(x)和密度函数fX(x)分别为
特别地,当取μ=0,此时称X服从单参数Laplace分布,记为X~L(β);而若取μ=0,β=1,此时X~L(1),称X服从标准Laplace分布。
两参数对称Laplace分布由于它与正态分布相比具有尖峰厚尾的特性而使得它在工程科学、质量控制、环境科学以金融等领域得到了广泛的应用。鉴于两参数对数Laplace分布与两参数对称Laplace分布的对数关系,所以关于两参数对数Laplace分布的统计分析可以通过分析两参数对称Laplace分布来实现。关于两参数对称Laplace分布的统计分析及应用已有许多文献作了较为深入的研究。Pedro Puig和Michael A.Stephens在文献[1]中通过4个实例研究了两参数对称Laplace分布的拟合检验问题。王振杰等[2]推导了两参数对称Laplace分布总体中位数的概率密度函数,证明了位置参数的极大似然估计是无偏的。唐林俊等[3]通过对深沪两地股票市场的股指收益率数据进行分析,发现两地股票收益率分布均呈“尖峰厚尾”的特性,为此引入两参数对称Laplace分布代替过去人们常用的正态分布去刻画收益率分布,结果显示Laplace分布比正态分布拟合效率有了明显的提高。杜红军等[4]采用两参数对称Laplace分布来刻画尖峰厚尾性,给出了金融资产的VaR和CVaR风险的计算和估计。王炳章[5]证明了两参数对称Laplace分布(原文献称其为对称指数分布)位置参数的极大似然估计为样本中位数,并证明了位置参数的极大似然估计具有无偏性与强相合性,同时还证明了刻度参数的估计也具有强相合性。徐美萍等[6]研究单参数Laplace分布的贝叶斯点估计,并用上证指数收益率数据作了实证分析。张永芳等[7]根据金融资产收益率的实际分布具有尖峰厚尾特性,引入两参数对称Laplace分布,得到了风险价值VaR和条件风险价值CVaR的计算公式,并采用沪深股市的股票进行了实证研究。赵志文等[8]研究两个单参数Laplace分布总体在数据有部分缺失的情形下参数的估计及相关假设检验问题。就目前关于两参数对称Laplace分布的统计分析而言大都涉及参数的点估计(包括极大似然估计与贝叶斯估计等),而参数的区间估计的研究却很少涉及。
1 两参数对数Laplace分布的特征性质
利用高等数学的知识容易得到如下关于两参数对数Laplace分布密度函数、失效率函数的图像特征以及数字特征:
定理:设某产品的寿命T服从两参数对数Laplace分布,T~LNL(μ,β),则T有如下特征性质:
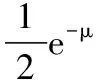
2) 失效率函数λT(t)的图像特征为:当β<1时,λT(t)在t∈(0,eμ)上严格单调增加,在t∈[eμ,+∞)上严格单调下降;当β=1时,λT(t)在t∈(0,eμ)上严格单调增加,在t∈[eμ,+∞)上严格单调下降;当β>1时,λT(t)在t∈(0,eμ)上严格单调下降,后严格单调增加,在t∈[eμ,+∞)上严格单调下降。
2 两参数对数Laplace分布全样本场合下参数的点估计与区间估计
首先,分别给出单参数Laplace分布总体和两参数对称Laplace分布总体全样本场合下参数的极大似然估计。
引理1:设总体X服从单参数Laplace分布,X~L(β),X1,X2,…,Xn是来自总体X的容量为n的一个简单随机样本,其次序统计量记为X(1),X(2),…,X(n),则参数β的极大似然估计为
引理2:设X1,X2,…,Xn是来自总体X服从两参数对称Laplace分布L(μ,β)的一个容量为n的简单随机样本,其对应的样本观察值为x1,x2,…,xn,次序统计量记为X(1),X(2),…,X(n),对应的次序观察值为x(1),x(2),…,x(n),则
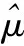
2) 刻度参数β的极大似然估计为:
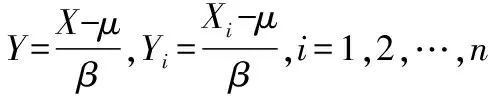
2.1 位置参数μ的区间估计
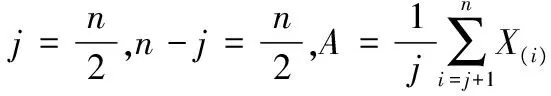
于是F(μ)是仅含有参数μ的枢轴量,又F(μ)为μ的严格单调增函数,且
由此,给定显著性水平α,枢轴量F(μ)的上侧1-α/2,α/2的分位数记为F1-α/2和Fα/2,易见参数μ的置信水平1-α的区间估计为:
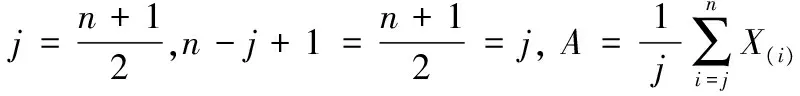
于是F(μ)是仅含有参数μ的枢轴量,又F(μ)为μ的严格单调增函数,且
由此,给定显著性水平α,枢轴量F(μ)的上侧1-α/2,α/2的分位数记为F1-α/2和Fα/2,易见参数μ的置信水平1-α的区间估计为
取样本容量n=3(1)30,通过10 000次Monte-Carlo模拟得F(μ)的0.99,0.95,0.90,0.85,0.15,0.10,0.05,0.025,0.01的上侧分位数,如表1所示。
2.2 刻度参数β的区间估计
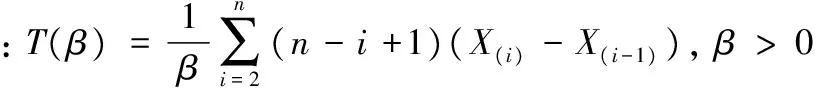
又
于是T(β)是仅含有参数β的枢轴量,又T(β)是β的严格单调减函数。
给定显著性水平α,枢轴量T(β)的上侧1-α/2,α/2的分位数分别记为T1-α/2和Tα/2,参数β的置信水平1-α的区间估计为
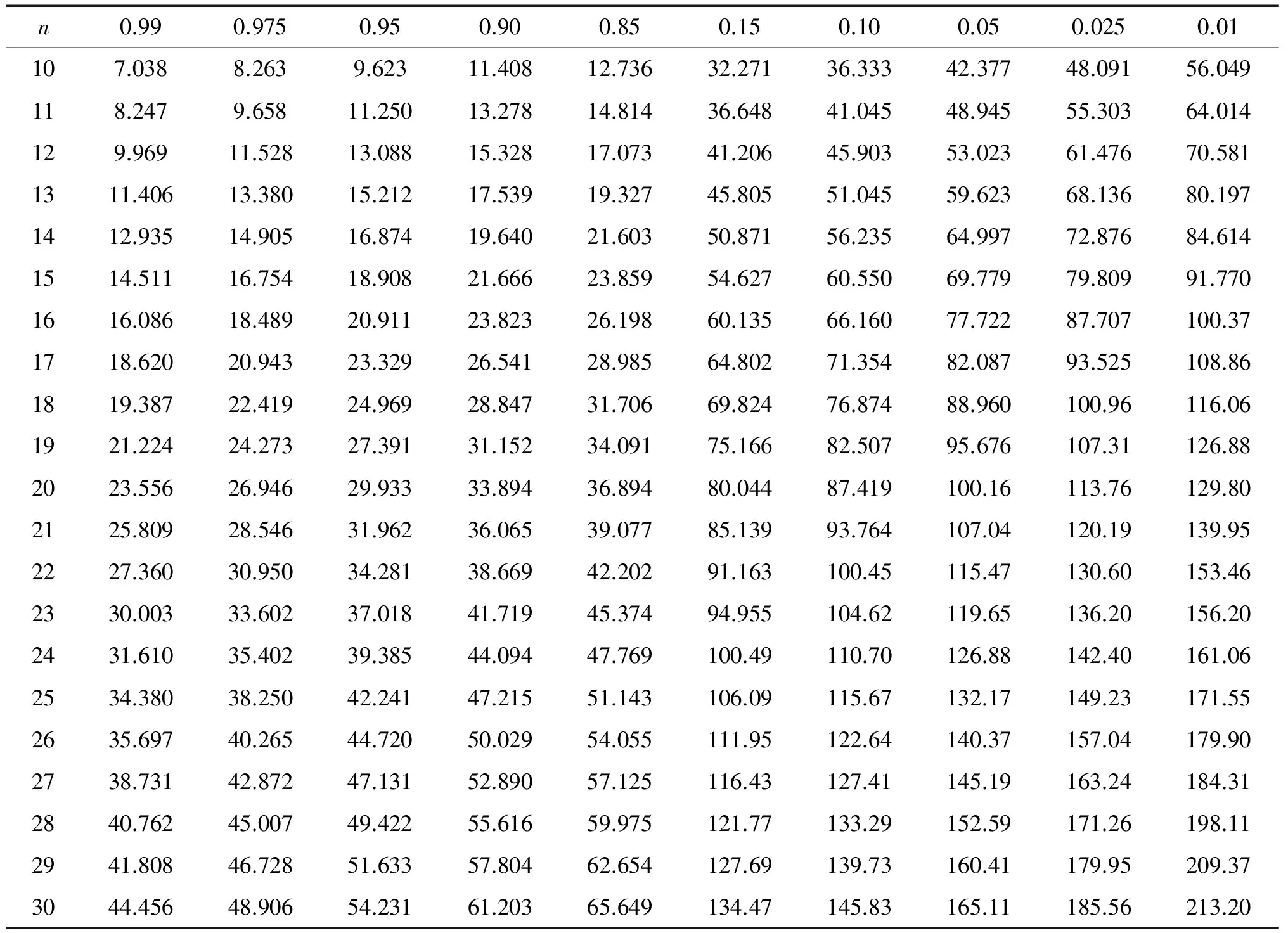
取样本容量n=3(1)30,通过10 000次Monte-Carlo模拟得T(β)的0.99,0.95,0.90,0.85,0.15,0.10,0.05,0.025,0.01的上侧分位数,如表2所示。
2.3 模拟分析
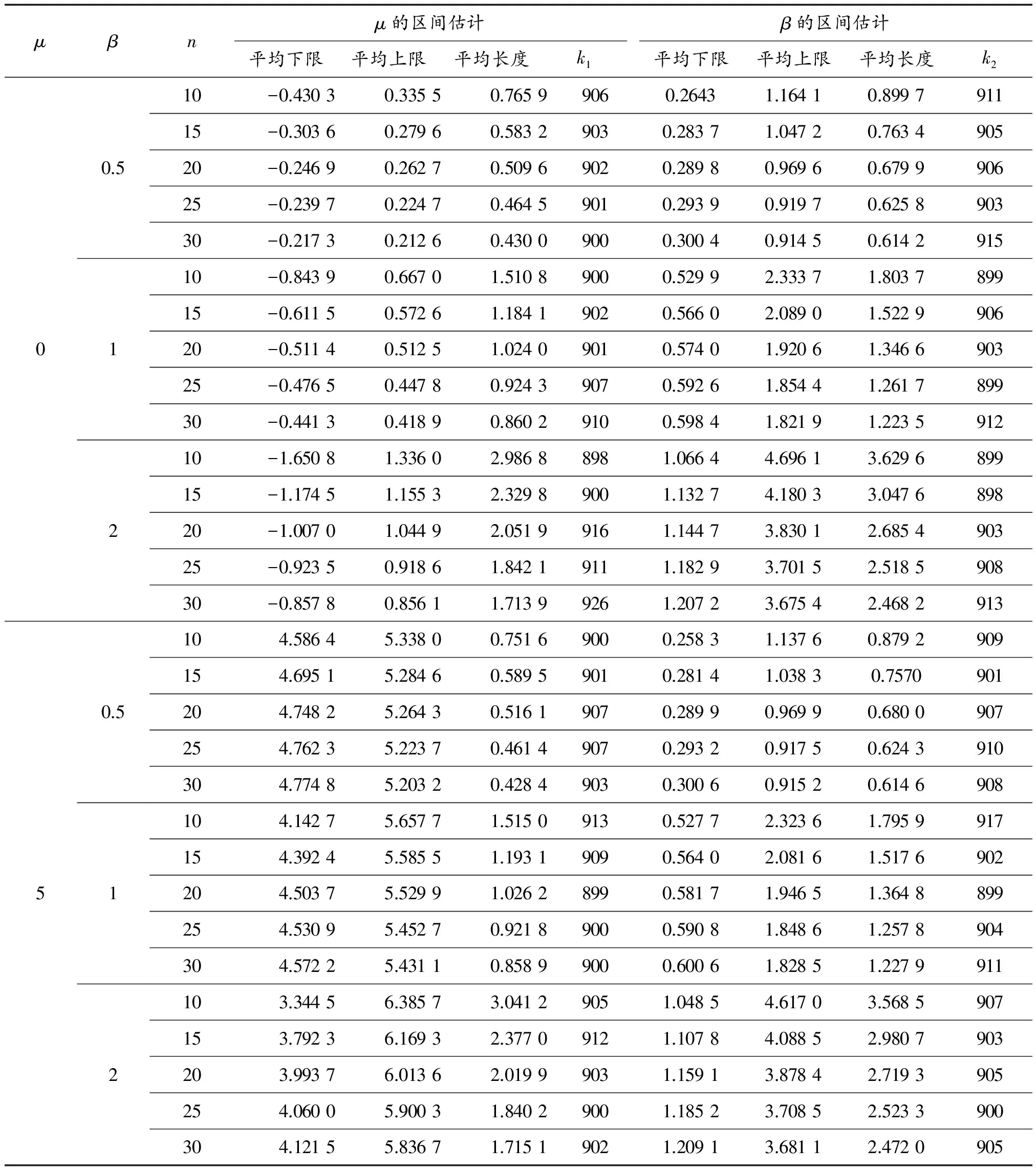
给定置信水平1-α=0.90,取样本容量n=5(5)30,参数真值取为μ=-5,0,5,β=0.5,1,2通过1 000次Monte-Carlo模拟得参数μ,β的区间估计的平均下限、平均上限和平均长度,同时统计1 000次模拟所得的区间估计包含参数真值的次数,结果如表3所示,其中k1,k2分别表示参数μ,β区间估计包含参数真值的次数。从中可以看到:
1) 固定参数真值,区间估计的长度随样本容量的增加而变小,即区间估计愈精确;
2)k1,k2的值大多在900以上,这也说明置信水平达到了0.90。
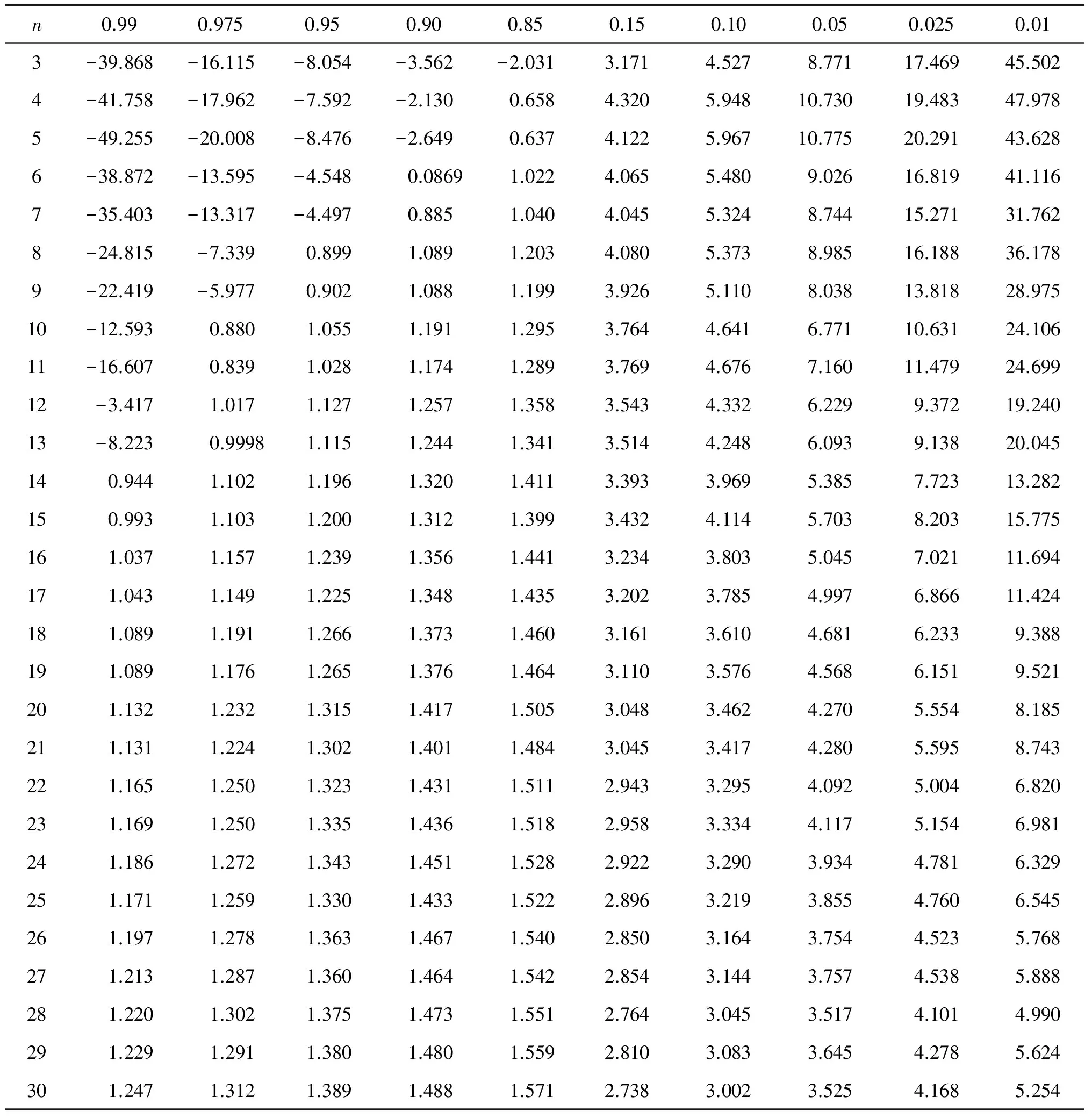
表1 枢轴量F(μ)的上侧分位数
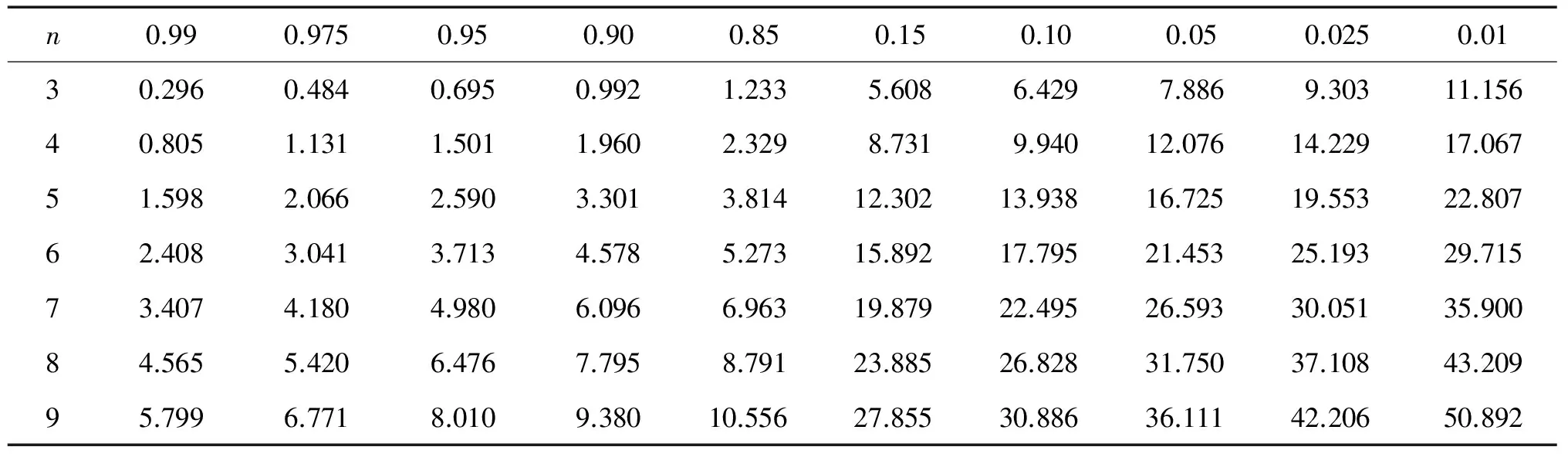
表2 枢轴量T(β)的上侧分位数
续表(表2)

表3 两参数对称Laplace分布参数μ,β区间估计的1 000次模拟
续表(表3)
μβnμ的区间估计平均下限平均上限平均长度k1β的区间估计平均下限平均上限平均长度k200.51210-0.43030.33550.76599060.26431.16410.899791115-0.30360.27960.58329030.28371.04720.763490520-0.24690.26270.50969020.28980.96960.679990625-0.23970.22470.46459010.29390.91970.625890330-0.21730.21260.43009000.30040.91450.614291510-0.84390.66701.51089000.52992.33371.803789915-0.61150.57261.18419020.56602.08901.522990620-0.51140.51251.02409010.57401.92061.346690325-0.47650.44780.92439070.59261.85441.261789930-0.44130.41890.86029100.59841.82191.223591210-1.65081.33602.98688981.06644.69613.629689915-1.17451.15532.32989001.13274.18033.047689820-1.00701.04492.05199161.14473.83012.685490325-0.92350.91861.84219111.18293.70152.518590830-0.85780.85611.71399261.20723.67542.468291350.512104.58645.33800.75169000.25831.13760.8792909154.69515.28460.58959010.28141.03830.7570901204.74825.26430.51619070.28990.96990.6800907254.76235.22370.46149070.29320.91750.6243910304.77485.20320.42849030.30060.91520.6146908104.14275.65771.51509130.52772.32361.7959917154.39245.58551.19319090.56402.08161.5176902204.50375.52991.02628990.58171.94651.3648899254.53095.45270.92189000.59081.84861.2578904304.57225.43110.85899000.60061.82851.2279911103.34456.38573.04129051.04854.61703.5685907153.79236.16932.37709121.10784.08852.9807903203.99376.01362.01999031.15913.87842.7193905254.06005.90031.84029001.18523.70852.5233900304.12155.83671.71519021.20913.68112.4720905
3 两参数对数Laplace分布定数截尾场合下参数的点估计与区间估计
设总体T服从两参数对数Laplace分布LNL(μ,β),T(1),T(2),…,T(r)是来自总体T的容量为n的前r个次序统计量。
令X=lnT,X(i)=lnT(i),i=1,2,…,r,则X~L(μ,β),而X(1),X(2),…,X(r)是来自总体X的容量为n的前r个次序统计量。
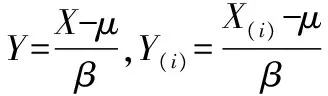
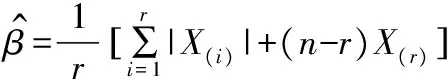
3.1 位置参数μ的点估计与区间估计
1) 当r≥[n/2]+1时,参数μ的点估计可取为
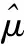
2) 当r<[n/2]+1时
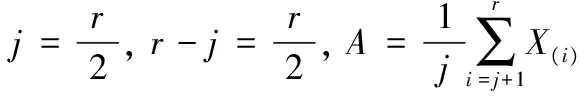
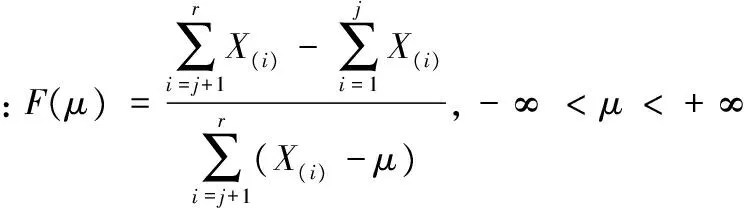
于是F(μ)是仅含有参数μ的枢轴量,又F(μ)为μ的严格单调增函数,且
则参数μ的点估计为
给定显著性水平α,枢轴量F(μ)的上侧1-α/2,α/2的分位数记为F1-α/2和Fα/2,易见参数μ的置信水平1-α的区间估计为:
值得指出的是上述所得到的参数μ的区间估计对r≥[n/2]+1也是成立的。
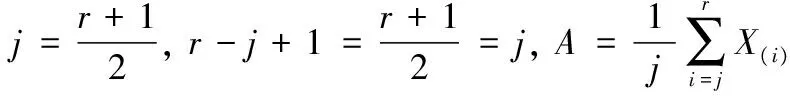
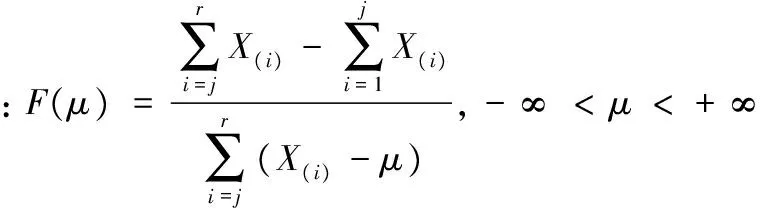
于是F(μ)是仅含有参数μ的枢轴量,又F(μ)为μ的严格单调增函数,且
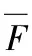
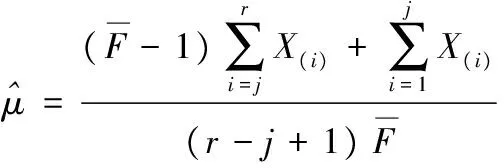
给定显著性水平α,枢轴量F(μ)的上侧1-α/2,α/2的分位数记为F1-α/2和Fα/2,易见参数μ的置信水平1-α的区间估计为
值得指出的是上述所得到的参数μ的区间估计对r≥[n/2]+1也是成立的。
3.2 刻度参数β的点估计与区间估计
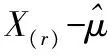
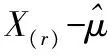
2) 构造如下仅含有参数β的枢轴量:
又
于是T(β)是仅含有参数β的枢轴量,又T(β)是β的严格单调减函数。
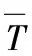
则参数β的点估计为
给定显著性水平α,枢轴量T(β)的上侧1-α/2,α/2的分位数分别记为T1-α/2和Tα/2,参数λ的置信水平1-α的区间估计为
4 两参数对数Laplace分布数据缺失场合下参数的点估计与区间估计
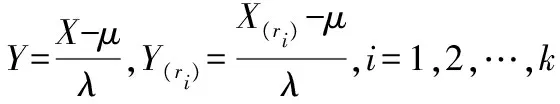
4.1 位置参数μ的点估计与区间估计
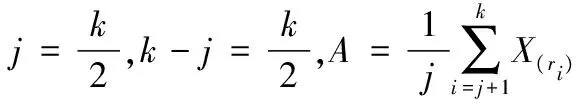
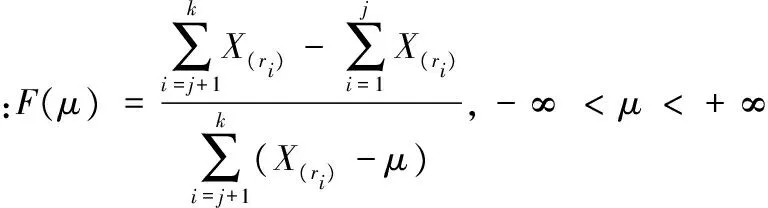
于是F(μ)是仅含有参数μ的枢轴量,又F(μ)为μ的严格单调增函数,且
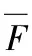
则参数μ的点估计为
给定显著性水平α,枢轴量F(μ)的上侧1-α/2,α/2的分位数记为F1-α/2和Fα/2,易见参数μ的置信水平1-α的区间估计为
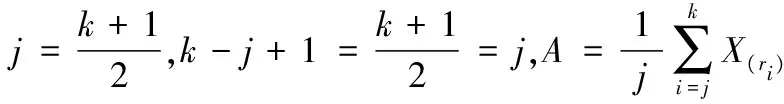

于是F(μ)是仅含有参数μ的枢轴量,又F(μ)为μ的严格单调增函数,且
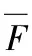
则参数μ的点估计为
给定显著性水平α,枢轴量F(μ)的上侧1-α/2,α/2的分位数记为F1-α/2和Fα/2,易见参数μ的置信水平1-α的区间估计为
4.2 刻度参数β的点估计与区间估计
又
于是T(β)是仅含有参数β的枢轴量,又T(β)是β的严格单调减函数。
则参数β的点估计为
给定显著性水平α,枢轴量T(β)的上侧1-α/2,α/2的分位数分别记为T1-α/2和Tα/2,参数β的置信水平1-α的区间估计为
5 实例分析
下面通过文献[1]中所涉及的两个服从两参数对称Laplace分布X~L(μ,β)的实例数据说明本文方法的应用。
文献[1]提供的100个纱线断裂强度数据,从小到大排序为:62,66,78,79,80,84,84,85,85,86,86,87,88,88,89,89,91,91,91,91,92,92,92,92,93,94,94,94,95,95,95,96,96,96,96,96,97,97,97,97,97,97,98,98,98,98,98,98,98,99,99,99,99,99,100,100,100,100,100,101,101,101,101,102,102,102,102,102,102,102,103,103,103,103,104,104,104,104,104,104,105,105,106,107,107,109,110,111,111,111,111,114,115,117,122,132,132,137,137,138。
1) 在全样本场合下,易见参数的极大似然估计为
利用本文方法,通过Monte-Carlo模拟当n=100时枢轴量F(μ)的上侧0.975,0.95,0.05,0.025分位数分别为:1.558 69,1.618 75,2.606 81,2.776 97,枢轴量T(β)的上侧0.975,0.95,0.05,0.025分位数分别为:272.172,291.44,679.648,758.688。于是可得参数μ的置信水平0.90,0.95的区间估计分别为:(97.460 5,101.357)和(97.064 4,101.748),而参数β的置信水平0.90,0.95的区间估计分别为:(5.505 79,12.839 7)和(4.932 2,13.748 7)
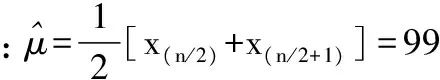
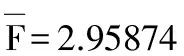
作为比较,参数μ的点估计也可取为:
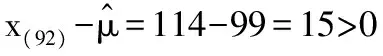
作为比较,参数β的点估计也可取为
若给定置信水平0.90,0.95,则可知参数μ的区间估计分别为:(97.036 2,100.316)和(96.692 6,100.622),而参数β的区间估计分别为:(5.380 38,12.810 3)和(4.900 16,13.601 7)。
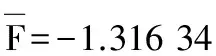
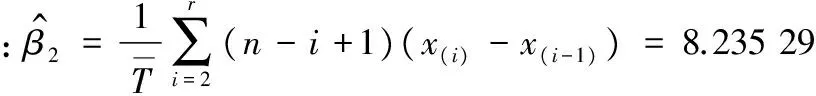
若给定置信水平0.90,0.95,则可知参数μ的区间估计分别为:(95.578 5,103.293)和(95.122,104.428),而参数β的区间估计分别为:(5.001 05,14.804 3)和(4.428 14,16.066 2)。
4) 若这100个数据仅保留15个数据:x(1),x(2),x(3),x(4),x(5),x(12),x(25),x(83),x(86),x(87),x(92),x(93),x(94),x(95),x(100),此时r1=1,r2=2,r3=3,r4=4,r5=5,r6=12,r7=25,r8=83,r9=86,r10=87,r11=92,r12=93,r13=94,r15=100,而k=15,j=8。
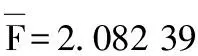
参数μ的点估计为:
参数β的点估计为:
若给定置信水平0.90,0.95,则可知参数μ的区间估计分别为:(95.527 7,103.028)和(94.796 2,103.713),而参数β的区间估计分别为:(6.173 08,11.654 7)和(5.737 09,12.277 9)。
[1] PEDRO P,MICHAEL A S.Tests of Fit for the Laplace Distribution with Applications[J].Technometrics,2000,42(4):417-424.
[2] 王振杰,欧吉坤,曲国庆.一元Laplace分布的L1-范估计的无偏性[J].武汉大学学报(信息科学版),2001,26(4):361-363.
[3] 唐林俊,杨虎.深沪股市收益率分布特征的统计分析[J].数理统计与管理,2004,23(5):1-4.
[4] 杜红军,刘小茂.拉普拉斯分布下的VaR和CVaR风险计算[J].应用数学,2006(S):225-228.
[5] 王炳章.对称指数分布的参数估计及其优良性[J].烟台大学学报,2007,20(4):250-253.
[6] 徐美萍,段景辉.Laplace分布参数估计的损失函数和风险函数的Bayes推断[J].统计与决策,2010(1):13-14.
[7] 张永芳,张全元.基于Laplace分布和CVaR的投资组合模型研究[J].重庆工商大学学报,2014,31(4):1-7.
[8] 赵志文,刘洋萍,于薇.具有部分缺失数据的两个拉普拉斯分布总体参数的估计与检验[J].吉林师范大学学报,2015(3):61-64.
[9] BAIN L J,ENGLEHART M.Interval Estimation for the Two Parameter Double Exponential Distribution[J].Technometrics,1973,15:875-887.
(责任编辑 唐定国)
Statistical Analysis Method Study of the Life with Two-Parameter Logarithmic Laplace Distribution
XU Xiao-ling1, GU Bei-qing1, WANG Rong-hua2
(1.School of Statistics and Information, Shanghai University of International Businessand Economics, Shanghai 201620, China; 2.College of Mathematics and Physics,Shanghai Normal University, Shanghai 200234, China)
A new life distribution called two-parameter logarithmic Laplace distribution was proposed. The image characteristics of density function and failure rate function as well as the numerical characteristics were studied for this distribution. Then the point estimates and interval estimates of location parameter and scale parameter were respectively researched under complete sample, type-I censored sample and missing data. To meet the needs of practitioners, we listed parts of quantile tables of pivotal quantity. Finally, one example was illustrated for the application of methods.
two-parameter logarithmic Laplace distribution; complete sample; type-I censored sample; missing data; point estimate; interval estimate
2016-11-23;
2016-12-25
国家自然科学基金资助项目(11671264)
徐晓岭 (1965—),男,博士,教授,主要从事可靠性统计研究。
10.11809/scbgxb2017.04.036
徐晓岭, 顾蓓青,王蓉华.寿命服从两参数对数Laplace分布的统计分析方法研究[J].兵器装备工程学报,2017(4):169-178.
format:XU Xiao-ling, GU Bei-qing, WANG Rong-hua.Statistical Analysis Method Study of the Life with Two-Parameter Logarithmic Laplace Distribution[J].Journal of Ordnance Equipment Engineering,2017(4):169-178.
O213
A
2096-2304(2017)04-0169-10

