大椭圆轨道卫星姿态基准坐标系与运动学研究

张大伟,程卫强

(1.上海卫星工程研究所,上海 201109; 2.上海航天技术研究院,上海 201109)



大椭圆轨道卫星姿态基准坐标系与运动学研究

张大伟1,程卫强2

(1.上海卫星工程研究所,上海 201109; 2.上海航天技术研究院,上海 201109)

针对大椭圆轨道卫星在轨运行中特殊光照条件导致的能源供给、热控设计等工程研制难点，兼顾光照时间和遥感任务，提出将基于太阳矢量与地面物点矢量的日地观测坐标系作为卫星姿态控制的基准坐标系。研究了相应的卫星姿态运动学，针对日地观测坐标系的角速度矢量在物理层面难以写出解析表达式的问题，提出一种解析计算方法，给出了算法流程，推导了日地观测坐标系相对惯性坐标系的角速度矢量在惯性坐标系中的计算公式。与数值差分法的仿真对比结果表明：该解析算法正确可行，其曲线特性和计算精度优于数值差分法。研究对卫星研制具有理论意义和应用价值。

大椭圆轨道； 闪电轨道； 姿态基准坐标系； 日地观测坐标系； 惯性坐标系； 姿态运动学； 相对角速度； 解析算法

0 引言

大椭圆轨道(HEO)是有较大偏心率的椭圆轨道，其近地点高度通常与低轨卫星相当，而远地点高度一般大于地球静止轨道(GEO)。由开普勒定律可知：具较大偏心率轨道的卫星在远地点附近的运行速度远小于近地点附近，故卫星一轨内大部分时间均运行于远地点附近的轨道段。有较大轨道倾角的HEO卫星能覆盖地球的极地地区，这样的轨道特性可用于高纬度地区的地球、通信及数据中继等空间任务，很大程度上能弥补GEO卫星不能覆盖高纬度地区的不足。为使卫星能长期保持在固定的北半球上空飞行，需HEO同时具有冻结轨道和逗留轨道的特性。冻结轨道需满足轨道近地点幅角不变，即轨道倾角为临界轨道倾角；逗留轨道需存在卫星星下点满足地理经度的逗留，即在某一时刻卫星星下点的地理经度变化率为零。闪电(Molniya)轨道是满足上述条件的一种特殊HEO，其命名源于20世纪60年代的前苏联闪电卫星，是一种采用临界轨道倾角、具有逗留轨道特性(远地点为逗留点)、轨道周期约12 h(地面轨迹2圈后回归)的HEO，其半长轴26 554.29 km，偏心率0.737 8，轨道倾角63.435°，近地点幅角270°，远地点(轨道高度约40 000 km)位于北半球高纬度地区，具有长期保持在北半球上空的“逗留”特征，1个周期内90%以上的弧段位于北半球上空，对北半球地区有很好的观测覆盖特性[1]。HEO实际应用于遥感任务时，多采用闪电轨道或与其类似的准闪电轨道，主要差别是将轨道的逗留特性这一约束条件替换为近地点轨道高度等约束条件，其对星下点轨迹的影响主要体现在远地点附近的曲线形状，本文的HEO专指上述(准)闪电轨道。

HEO卫星相对中高纬度地区具“准静止”的特点，与中高纬度地区目标有较好的星地相对关系，因此已被俄罗斯(前苏联)、美国等用于遥感及环境探测、电子侦察和天基预警等领域[2-4]。目前，对HEO卫星的研究主要有卫星在轨空间环境的影响、组网运行方式、变轨与交会、组合导航、轨道性能分析和轨迹保持策略等[5-11]。目前在卫星研制过程中普遍应用姿态基准坐标系为轨道坐标系，即Z轴指向地心，Y轴沿卫星轨道面的负法向方向，X轴与Y、Z轴符合右手法则[12]。由轨道相关分析可知：HEO升交点赤经的年变化率约53°，太阳矢量与卫星轨道面夹角的年最大变化范围为-87°～+87°，且有2次正负切换。因此，在轨道坐标系为姿态基准坐标系时，HEO卫星的能源供给、热控设计、飞行方案等设计问题将会变得复杂，对卫星的工程设计研制带来诸多困难。此外，若卫星任务需要其姿态指向地面固定的物点或区域，则卫星姿态可能会长时间保持大角度变化，这无疑将使卫星光照条件产生附加的变化，使工程设计研制更为复杂。

针对上述问题，从HEO的轨道特性与卫星任务出发，本文提出了一种基于太阳方向和地面物点的日地观测坐标系，作为HEO卫星姿态控制的新基准坐标系，并研究了在此坐标系中的卫星姿态运动学，针对运动学方程中日地观测坐标系的角速度难以写出解析表达式的问题，提出了一种星上可用的角速度解析计算方法，从而完善了新姿态基准坐标系的基础理论与工程实用性，并与数值差分方法进行了计算机仿真对比验证。

1 卫星姿态基准坐标系

由前述可知，HEO的特性将给采用传统轨道坐标系的卫星带来能源供给、热控设计、飞行方案等诸多问题。为避免这些问题，本文提出一种兼顾卫星光照条件与遥感任务的日地观测坐标系，代替传统的轨道坐标系作为新姿态基准坐标系。定义日地观测坐标系os-xsyszs：坐标系原点os与卫星质心重合；oszs轴沿卫星质心指向地面观测的物点；osxs轴位于太阳矢量rsun与oszs轴形成的平面内，沿rsun相反的方向且与oszs轴垂直；osys轴按右手法则定义。坐标系如图1所示。

由上述定义可知：日地观测坐标系可定义的前提条件为rsun与oszs轴不平行，若平行，则osxs、osys轴将无法唯一确定。在工程实际应用中，由于卫星在轨道上运行，rsun与oszs轴的平行仅发生在极短的时间内，因此当两个矢量平行时，可设定各坐标轴惯性保持。另外，由于黄赤交角约23.5°，即两个矢量的平行仅可能发生在低纬度地区(如当卫星位于赤道附近上空时，Z轴沿太阳光线方向指向地面)，而在高纬度地区的长时间工作阶段并不会发生，因此各坐标轴惯性保持的策略是合理可行的。

由日地观测坐标系定义，卫星太阳电池阵只需在本体坐标系的俯仰轴方向进行一维驱动，即可保证卫星具有良好的光照条件与能源供给，简化星上热控设计，并能使卫星本体坐标系偏航轴方向(遥感载荷对地方向)始终指向地面物点或观测区域，即保证卫星遥感任务有足够的自由度[12]。

另外，若需要遥感载荷保持对星下点进行观测，即需要卫星姿态基准坐标系的Z轴指向卫星星下点(与轨道坐标系Z轴指向星下点的目的相同)，则只需设日地观测坐标系定义中的地面物点为地心即可，即地面物点的位置矢量为零。

2 卫星姿态运动学

基于日地观测坐标系的卫星运动学方程，用姿态四元数表示为

(1)

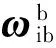
(2)

3 卫星姿态基准相对惯性坐标系的姿态角速度求解

3.1 卫星位置与速度矢量(惯性坐标系中)

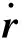
(3)

(4)

(5)

(6)

式中：μ为地心引力常数；rs为卫星的地心距，且rs=as(1-(es)2)/(1+escosfs)[13]。

3.2 太阳单位位置与速度矢量(惯性坐标系中)

(7)

式中：usun为太阳的纬度幅角，且usun=fsun+ωsun；Rx(α)，Rz(α)分别为绕x、z轴旋转α的姿态变换矩阵[12]。在惯性坐标系中，太阳单位位置矢量的角速度矢量

(8)

式中：nsun为太阳矢量的角速率，且

此处：μsun为日心引力常数。则在惯性坐标系中，太阳单位位置矢量的速度矢量满足

(9)

3.3 地面物点的位置与速度矢量(惯性坐标系中)

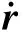
(10)

(11)

式中：Rp，Re分别为地球的极半径和赤道半径。由文献[15]，在WGS-84地固坐标系中，地面物点的单位位置矢量

(12)

则地固坐标系中地面物点的位置矢量和角速度矢量分别为

(13)

ωew=[0 0ωe]T

(14)

式中：ωe为地球自转的角速率。惯性坐标系中，地面物点的位置与速度矢量分别为

(15)

(16)

式中：Rwi为惯性坐标系至地固坐标系的姿态变换矩阵，且

(17)

此处：RPR，RNR，REP分别为岁差、章动和极移矩阵；SG为格林尼治平恒星时，且

SG=(18.697 374 6+879 000.051 336 7TT+

0.093 104(TT)2/3 600)×15×π/180

(18)

其中：TT为当前时刻的儒略世纪数[13]。

3.4 日地观测坐标系坐标轴矢量(惯性坐标系中)

由前述日地观测坐标系的定义，惯性坐标系中日地观测坐标系的各坐标轴单位矢量分别为

(19)

(20)

(21)

(22)

3.5 日地观测坐标系相对惯性坐标系的角速度矢量(惯性坐标系中)

惯性坐标系中，对日地观测坐标系的各坐标轴单位矢量求导，可得

(23)

(24)

(25)

(26)

根据文献[12]，由姿态变换矩阵的性质可知：该导数满足关系

(27)

(28)

因Rsi可逆，则有

(29)

在惯性坐标系中日地观测坐标系相对惯性坐标系的角速度

(30)

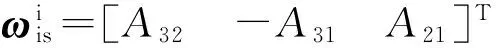
(31)

4 仿真对比验证

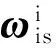
仿真中，设HEO为标准的闪电轨道(即半长轴26 554.29km、偏心率0.737 8、轨道倾角63.435°、近地点幅角270°)，卫星运行约1轨(即仿真时长12h)，卫星运行起始点为近地点(即初始时刻卫星平近点角为0°)，地面物点的经纬度分别为东经125°、北纬45°。用解析算法选取上三角元素、下三角元素、数值差分方法计算，所得日地观测坐标系的角速度分别如图3～5所示。解析算法的上、下三角元素与数值差分方法的误差分别如图6、7所示。

由仿真结果可知：

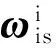
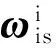
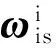
5 结束语

针对由于大椭圆轨道特殊的光照条件导致卫星能源供给、热控设计、飞行方案等复杂化，本文提出了一种基于太阳矢量和地面物点矢量的日地观测坐标系，作为大椭圆轨道卫星姿态控制的基准坐标系，在此基础上分析了卫星姿态运动学。针对运动学方程中日地观测坐标系相对惯性坐标系的角速度矢量难以写出解析表达式的问题，提出了一种解析的计算方法。为验证此种解析算法的正确性，与数值差分方法进行了仿真对比验证。仿真计算结果表明：解析算法正确可行，且较数值差分方法有更好的曲线光滑性，无尖峰与跳变问题，同时具更高的计算精度。本文提出的日地观测坐标系从基础理论上解决了大椭圆轨道特殊的光照条件带来的能源供给、热控设计、飞行方案等的复杂化问题，明显简化了大椭圆轨道卫星的研制设计过程。本文的日地观测坐标系角速度矢量的解析计算方法，从工程实际解决了基于日地观测坐标系的运动学方程的完整性问题，使卫星在轨运行时的精确姿态控制成为可能，有很强的工程实用性，对卫星研制有重要的理论意义和应用价值。虽然本文提出的日地观测坐标系与运动学中角速度的解析算法是由HEO的特点与问题引出的，但就其概念与方法来说有较好的普适性，如日地观测坐标系同样适于其它光照条件变化频繁剧烈的特殊轨道，可解决类似的工程设计复杂化问题，而运动学中角速度的解析算法同样适于各种姿态运动学中姿态基准坐标系角速度的计算问题，有较好的通用性。

[1] ILCEV S D. Highly elliptical orbits (HEO) for high latitudes and polar coverage[C]// 20th International Crimean Conference: Microwave & Telecommunication Technology. Sevastopol: [s. n.], 2010: 396-399.

[2] ASMUS V V, DYADYUCHENKO V N, NOSENKO Y I, et al. A highly elliptical orbit space system for hydrometeorological monitoring of the Arctic region[J]. Bulletin of the World Meteorological Organization， 2007, 56(4): 293-296.

[3] 张维胜, 王红兵, 李辉. 美国军用卫星现状与性能[J]. 中国航天, 2001(6): 42-44.

[4] 王震, 邓大松. 俄罗斯天基预警系统浅析[J]. 电子工程师, 2006, 32(3): 78-80.

[5] TRICHTCHENKO L D, NIKITINA L V, TRISHCHENKO A P, et al. Highly elliptical orbits for arctic observations: assessment of ionizing radiation[J]. Advances in Space Research, 2014, 54: 2398-2414.

[6] 安雪滢, 杨乐平, 张为华, 等. 大椭圆轨道航天器编队飞行相对运动分析[J]. 国防科技大学学报, 2005, 27(2): 1-5.

[7] 李化义, 张迎春, 强文义, 等. 大椭圆轨道卫星编队T-S模糊控制[J]. 宇航学报, 2007, 28(6): 1624-1627.

[8] 徐帷, 武海雷, 卢山, 等. 大椭圆轨道卫星交会高轨目标的高精度视线跟踪控制[J]. 空间控制技术与应用, 2015, 41(2): 6-11.

[9] 李璟璟, 张迎春, 郑靖, 等. 基于信息融合的大椭圆轨道卫星组合导航方法[J]. 宇航学报, 2012, 33(9): 1233-1240.

[10] 佘明生. 大椭圆轨道上空间探测卫星轨道性能分析[J]. 空间科学学报, 1998, 18(4): 348-355.

[11] 杨悦, 吴功友, 白沁园, 等. 回归大椭圆轨道卫星轨迹保持策略与仿真[J]. 科学技术与工程. 2013, 13(26): 7711-7715.

[12] 章仁为. 卫星轨道姿态动力学与控制[M]. 北京: 北京航空航天大学出版社, 2006.

[13] 刘林. 航天器轨道理论[M]. 北京: 国防工业出版社, 2000.

[14] PADEN B, PANJA R. Globally asymptotically stable ‘PD+’ controller for robot manipulators[J]. International Journal of Control, 1988, 47(6): 1697-1712.

[15] 郗晓宁, 王威. 近地航天器轨道基础[M]. 长沙: 国防科技大学出版社, 2003: 17-18.

Study on Attitude Reference Frame and Kinematics for a Highly Elliptical Orbit Satellite

ZHANG Da-wei1, CHENG Wei-qiang2

(1. Shanghai Institute of Satellite Engineering, Shanghai 201109, China;2. Shanghai Academy of Spaceflight Technology, Shanghai 201109, China)

For the purpose of resolving the difficulty engineering problems, such as energy supply and thermal control design, caused for the special sun-light condition of a highly elliptical orbit satellite, a sun-earth sensing frame based on a sun vector and a target point on earth as an attitude reference frame was proposed when both the sun-light condition and remote sensor mission were in consideration in this paper. The attitude kinematics of satellite was researched. An analytical algorithm was proposed for calculating the angle velocity vector of the sun-earth sensing frame which was difficult to be expressed as an analytical form with physical method. The algorithm flowchart was given. The equations of angular velocity vector of sun-earth sensing frame relative to inertia frame which were in inertia frame were derived for solving attitude angular velocity. The results of comparison simulation between the analytical algorithm and a numerical differential calculation showed that the analytical algorithm was valid and feasible, and had the better characteristic of angle velocity curve and computational accuracy. The research has the theory significance and the application value for satellite development.

highly elliptical orbit; Molniya orbit; attitude reference frame; sun-earth sensing frame; inertia frame; attitude kinematics; relative angle velocity; analytical algorithm

1006-1630(2017)02-0067-07

2016-06-16；

2016-08-31

张大伟(1980—)，男，博士，高级工程师，主要研究方向为卫星轨道姿态动力学与控制，卫星总体设计。

V412.41

A

10.19328/j.cnki.1006-1630.2017.02.006