GPS实时定轨误差对姿态确定的影响分析

王文妍,杨盛庆， 2,吴敬玉,彭仁军

(1.上海市空间智能控制技术重点实验室,上海 201109; 2.上海航天控制技术研究所,上海 201109;3.上海卫星工程研究所,上海201109)



GPS实时定轨误差对姿态确定的影响分析

王文妍1,杨盛庆1， 2,吴敬玉1,彭仁军3

(1.上海市空间智能控制技术重点实验室,上海 201109; 2.上海航天控制技术研究所,上海 201109;3.上海卫星工程研究所,上海201109)

对GPS实时定轨误差对卫星姿态确定的影响进行了分析。因用位置、速度确定的坐标转换矩阵无法直接给出姿态角确定误差的解析表达，基于近圆、近极轨轨道假设，根据位置、速度和开普勒轨道六要素间的转换关系，给出了小姿态角偏差条件下转换矩阵的全微分形式，进而给出了各姿态角关于各轴分量的偏导数形式，在分别分析位置和测速误差对姿态角影响的基础上，给出了综合的姿态角确定误差，推导了姿态确定误差的解析表达式。研究发现：速度矢量主要引起偏航角的误差，对俯仰和滚动方向几乎无影响；位置矢量主要引起俯仰和滚动轴的姿态角误差，对偏航角方向几乎无影响。仿真结果验证了分析的正确性，并发现GPS定轨误差引起的姿态角确定误差小于0.001°，基本可忽略。

GPS接收机； 实时定轨； 惯性系位置、速度信息； 坐标转换； 姿态角误差； 开普勒轨道要素； 近圆轨道； 近极轨轨道

0 引言

在轨进行姿态确定时，星载计算机通常需根据当前轨道信息建立轨道坐标系。一般来说，由星上软件实现的轨道预报，其位置、速度精度受算法原理的制约，实时精度较低。特别地，随着时间积累，位置、速度的偏差会达到不容忽视的量级，这些定轨误差直接反映到姿态确定上，对姿态确定精度造成较大的影响[1]。为保证星上位置、速度的实时测量精度，可用星载GPS接收机进行轨道的精确定位[2-4]。目前，在轨运行3～5年的卫星GPS接收机实时定位精度为位置精度优于50米/轴、速度精度优于0.45 m/s；新一代的GPS接收机的实时定位精度为位置精度优于10米/轴、速度精度优于0.1 m/s。

分析定轨误差对姿态确定的影响，需给出惯性系至轨道坐标系的转换矩阵及其全微分形式。对一般的椭圆轨道，用笛卡尔坐标表述的转换矩阵，非线性较强，难以给出其全微分形式中偏导数的解析表达式。近地轨道的各类气象卫星、资源卫星多采用近圆、近极轨轨轨道[5-7]。针对此类卫星，进行GPS定轨误差对姿态确定的影响分析有充分的必要性，且此类轨道动力学特性较一般椭圆轨道更易描述，为误差影响的理论分析提供了可能。目前，国内在姿态角确定误差分析领域尚未有基于姿态角全微分解析形式的理论分析方法。本文在近圆、近极轨轨道假设的基础上，根据位置、速度和开普勒轨道六要素间的转换关系，给出了小姿态角偏差条件下转换矩阵的全微分形式，进而给出了各姿态角关于各轴分量的偏导数形式，分析了GPS定轨误差对姿态角的影响，给出了姿态确定误差的解析表达式，并通过仿真进行了验证。

1 轨道动力学

1.1 轨道坐标系

由卫星轨道坐标系的定义可知：根据某时刻的位置和速度矢量，卫星轨道坐标系相对地心惯性坐标系的转换矩阵Aoi可表示为

(1)

(2)

(3)

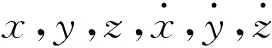
(4)

式中：

1.2 转换矩阵的全微分形式

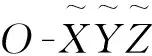
式中：C为转换矩阵间的传递系数矩阵，且

此处：φ，θ，ψ分别为滚动角、俯仰角和偏航角[9]。若转换矩阵间相差不大，则其误差可表示为

(5)

于是有

(6)

式中：E为单位阵。

(7)

式(7)右端可简记为

(8)

2 定轨误差对姿态角的影响

2.1 位置误差引起的姿态角确定误差

轨道的惯性系位置、速度与Kepler轨道要素的满足关系

(9)

(10)

式中：u为卫星轨道的纬度幅角；i为轨道倾角；Ω为升交点赤经[10-11]。

对近圆轨道，满足|r×v|≈|r||v|。Aoi关于x的偏导数、各姿态角关于x的误差满足

(11)

φx=ΔAx(2,3)Δx=[Δx/|r×v|]×

sinucosicosΩ)-(-sinusinΩ+

(12)

cosucosisinΩ]

(13)

cosucosicosΩ)-(-sinusinΩ+

cosucosicosΩ)(cosusini)]≈0

(14)

式中：

a31=cosusini

由上述误差公式可知：位置矢量在X轴上的误差Δx引起的姿态角确定误差主要影响φ，θ的误差，对ψ基本无影响。滚动角误差与误差Δx成正比，与升交点赤经的正弦成正比，与纬度幅角无关。俯仰角误差与误差Δx成正比，由于轨道倾角接近90°(近极轨轨道)，因此误差基本与升交点赤经的余弦成正比，与纬度幅角正弦成正比。

同理，可得各位置测量误差对姿态确定角的影响。结果见表1。

表1 位置测量误差对姿态确定角的影响Tab.1 Attitude errors caused by position detection

2.2 测速误差引起的姿态角确定误差

(15)

sini(-cosusinΩ-sinucosicosΩ)-

(-cosusinΩ-sinucosicosΩ)×

(-sinusini)]=0

(16)

(17)

(-sinusinΩ+cosucosicosΩ)+y(cosusini)]=

cosucosicosΩ)-(-cosusinΩ-

sinucosicosΩ)(cosusini)]≈

(18)

根据上述误差公式，可发现：位置矢量在Y轴上的误差Δy引起的姿态角确定误差主要影响滚动角和俯仰的误差，对偏航角基本无影响，滚动角误差与误差Δy成正比，与升交点赤经的余弦成正比，与纬度幅角无关，俯仰角误差与误差Δy成正比，由于轨道倾角接近90°，误差基本与升交点赤经的正弦成正比，与纬度幅角正弦成正比。

同理，可得各速度测量误差对姿态确定角的影响。结果见表2。

表2 速度测量误差对姿态确定角的影响Tab.2 Attitude errors caused by velocity detection

2.3 综合的姿态角确定误差

综上所述，GPS接收机的定轨误差导致的姿态角确定总误差最大值为

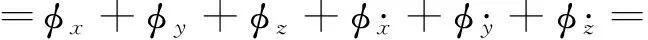
(cosi)Δz]+0+0+0

(19)

(-sinusinΩ+cosucosicosΩ)Δy-

(cosusini)Δz]+0+0+0

(20)

(21)

由式(19)～(21)可知：速度矢量基本引起偏航角的误差，对俯仰和滚动方向几乎无影响；相反，位置矢量主要引起俯仰和滚动轴的姿态角误差，对偏航角方向几乎无影响。

假设GPS的位置精度优于50m(单轴1σ)，测速精度优于0.45 m/s(单轴1σ)，取误差为随机误差，则最终得总的姿态角确定误差为：φ≈0.000 635°；θ≈0.000 63°；ψ≈0.000 48°。由此可得GPS提供的速度和位置误差引起的姿态角确定误差小于0.001°，该项误差基本可忽略。

3 仿真验证

3.1 位置误差引起的姿态角确定误差

设|r|=7 000 km，单轴位置误差1 000 m，则由该误差引起的姿态角确定误差见表3。此处：取误差大于GPS误差的目的是为通过仿真发现该误差对某些方向的影响确实几乎为0。

表3 位置测量误差影响的定量分析Tab.3 Numerical analysis of attitude errors caused by position detection

在位置误差[1 000 0 0] m，速度误差[0 0 0] m/s的条件下，仿真所得升交点赤经从0°开始，纬度幅角从0°开始，随时间变化，沿X轴方向的位置误差引起的姿态角误差的变化如图1所示。由图1可知：仿真曲线与理论分析的解析结果一致。

3.2 测速误差引起的姿态角确定误差

设|v|=7 544 m/s，单轴速度误差4.5 m/s，仿真所得由该误差引起的姿态角确定误差见表4。

在位置误差[0， 0， 0] m，速度误差[4. 5， 0， 0] m/s条件下，仿真所得纬度幅角从0°开始，随时间变化，沿X轴方向的速度误差引起的姿态角误差的变化如图2所示。由图2可知：仿真曲线与理论分析的解析结果一致。

表4 位置测量误差影响的定量分析Tab.4 Numerical analysis of attitude errors caused by velocity detection

3.3 姿态角确定综合误差

设位置误差[1 000 1 000 1 000] m，速度误差[4.5 4.5 4.5] m/s，仿真所得纬度幅角从0°开始，随时间变化，同时沿X、Y、Z轴方向的位置误差和速度误差所共同引起的姿态角确定误差的变化如图3所示。由图3可知：GPS的定轨误差引起的姿态角确定误差小于0.001°，与理论分析的解析结论基本一致。

4 结论

姿轨控系统中姿态确定算法使用的轨道信息通常由GPS实时定轨信息转换而来，分析GPS实时定轨误差对姿态确定误差的影响有重要的研究意义。针对近圆、近极轨轨道，本文给出了分析GPS定轨误差引起的姿态确定误差的理论分析方法。研究发现，由GPS定轨误差引起的姿态角确定误差表现为：位置矢量主要引起俯仰和滚动轴的姿态角确定误差，对滚动角方向几乎无影响；相反，速度矢量主要引起滚动角的误差，对俯仰和滚动方向几乎无影响。分析表明：由GPS定轨误差引起的姿态角确定误差小于0.001°，基本可忽略。本文的研究成果给出了基于GPS实现定轨信息的姿态角确定误差分析方法。由GPS定轨误差造成的姿态角偏差时姿态角确定误差的重要组成部分，本文的结论对卫星姿态确定的工程应用有实际的借鉴意义。

[1] 柳仲贵. 卫星轨道误差的相关性[J]. 飞行器测控学报, 2011, 30(5): 45-49.

[2] 方群, 王军武, 袁建平. 利用GPS系统确定小卫星姿态的一种算法[J]. 西北工业大学学报, 2003, 21(1): 14-17.

[3] 郑庆晖. 基于GPS的航天器姿态、相对姿态确定研究[D]. 长沙: 国防科学技术大学, 2003.

[4] 曹冲. GPS技术在卫星定轨和姿态确定中的应用[J]. 电波与天线, 1997, 22(4): 12-23.

[5] 孟执中, 李卿. 气象卫星的发展[J]. 上海航天, 2003, 20(2): 1-6.

[6] 孟执中. 中国的极轨气象卫星[J]. 中国工程科学, 2004, 6(10): 1-5.

[7] 杨维廉. 资源一号卫星轨道: 理论与实践[J]. 航天器工程, 2001, 10(1): 30-43.

[8] 刘林. 航天器轨道理论[M]. 北京: 国防工业出版社, 2000.

[9] 章仁为. 卫星轨道姿态动力学与控制[M]. 北京: 北京航空航天大学出版社, 1998.

[10] 杨嘉墀, 范剑峰. 航天器轨道动力学与控制[M]. 北京: 宇航出版社, 1995.

[11] 肖峰. 人造地球卫星轨道摄动理论[M]. 长沙: 国防科技大学出版社, 1997.

Analysis on Attitude Errors Caused by Real-Time Orbit Determination of GPS

WANG Wen-yan1, YANG Sheng-qing1, 2, WU Jing-yu1, PENG Ren-jun3

(1. Shanghai Key Laboratory of Aerospace Intelligent Control Technology, Shanghai 201109, China;2. Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China;3. Shanghai Institute of Satellite Engineering, Shanghai 201109, China)

The attitude errors caused by real-time orbit determination of GPS were analyzed in this paper. Because the analytical expression of attitude error could not be reached directly from position and velocity information, the full differential form of transfer matrix was given according to the relationship among position, velocity and Kepler orbit elements, which was based on assumption of near-circle and near-polar orbit. The partial derivation forms of the branch in three axes for the attitude angular were also given. Based on analyzing the effect of position errors and velocity errors on the attitude angular, the integrated determination errors of the attitude angular were obtained. The analytic expressions of the attitude errors were derived. It found that the velocity vector would bring on yaw angle error mainly and had a little effect on pitch angler and rolling angler, and the position vector would bring on pitch angler and rolling angler error mainly and had a little effect on yaw angler. The simulation results proved the correctness of the theory analysis. It is believed that the attitude error caused by real-time orbit determination of GPS is smaller than 0.001° which can be almost ignored.

GPS receiver; real-time orbit determination; position/velocity information in inertial frame; coordinate transformation; attitude error; Kepler orbit elements; near-circle orbit; near-polar orbit

1006-1630(2017)02-0144-06

2016-11-10；

2017-02-09

上海市青年科技启明星计划资助(17QB1401400)

王文妍(1975—)，女，研究员，主要研究方向为卫星轨道/姿态动力学与控制。

V482.22

A

10.19328/j.cnki.1006-1630.2017.02.016