我国股债联动的非线性特征分析

摘要：文章经过单位根检验、自回归模型的滞后阶数的确定、迟延参数的确定、非线性模型的选择和样本外预测等步骤，对我国股债的联动性进行了非线性特征分析，研究发现：沪深300指数与中证全债的联动性呈现非线性，其特征可通过LSTAR模型来刻画。

关键词：联动性 非线性 LSTAR模型

任何事物或现象的运动规律都可以描述为线性和非线性的。自然现象如此，社会经济现象也不例外，特别是在金融经济领域，许多金融时间序列的运动规律是非线性的，我国股债联动是否也是呈非线性关系，对这一问题的研究有利于深化对股债联动理论的认识，有利于投资者根据股债联动特征调整最优投资组合以获取最大收益，也有利于监管者完善监管政策以促进我国股票和债券市场进一步发展。

一、文献综述

赵春艳和南士敬（2011）对我国通货膨胀率以其滞后一阶为转换变量建立了LSTAR模型，结果显示该模型的拟合效果很好，这表明我国低通货膨胀与高通货膨胀之间存在明显的非线性转换特征。沈春华、许涤龙和路芸（2013）采用LSTR模型对我国通货膨胀率的非线性特征和动态波动路径进行了实证研究，结果显示：我国通货膨胀率呈现出明显的非线性特征，且经常在三区制间快速转移。通货膨胀率的转移速度较快，这在很大程度上表明我国货币政策的灵敏性、有效性和稳健性。谢朝华等（2010）对上海股市的分形与混沌特性的研究揭示了我国股市的非线性本质，在制定股市发展政策时应该以非线性观为指导。王成勇和艾春荣（2010）运用STAR模型理论对我国1979年第1季度至2009年第3季度的季度GDP增长率的研究表明我国GDP呈非线性运动。王晓燕和李美洲（2012）基于误差修正模型基础上的两机制门限协模型分析我国中期和长期国债收益率，结果发现我国中期和长期国债收益率存在非线性调整过程。目前还未见研究我国股债之间的联动非线性特征文献的报道，因此，本文的研究有利于填补这一空白。

二、平滑转换自回归（STAR）模型

（一）基本模型

三、实证分析

（一）数据选取

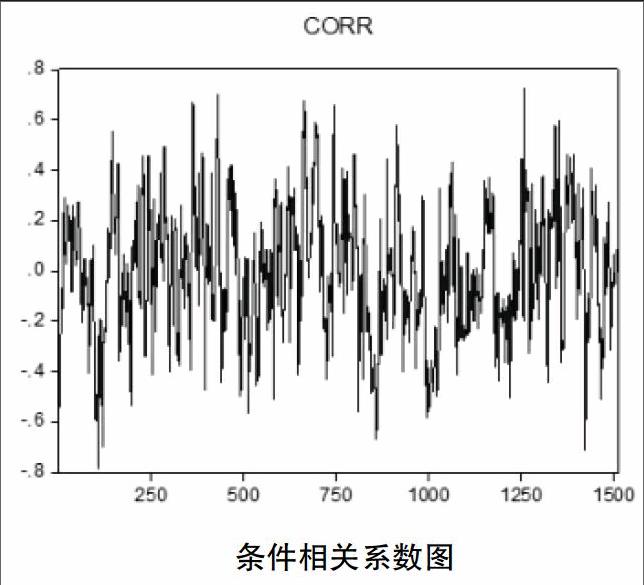
此处所用的数据为基于t分布的DCC-MVGARCH（1，1）模型计算出的沪深300指数与中证全债指数的动态条件相关系数。由于篇幅所限，不列出具体过程，只将图形和基本统计量描述出来，如下图所示。

本文将全流通时代——2008年4月17日到2016年9月30日分为两个区间，第一个区间是2008年4月17日—2014年6月30日，共1 506个数据；第二个区间是2014年7月1日—2016年9月30日，共608个数据。第一个区间的数据用来建立非线性平滑转换自回归模型，第二个区间的数据用来做样本外的预测，以评价平滑转换自回归模型的拟合效果。

首先将动态条件相关系数corr进行Fisher转换，这种转换可以将处于[-1，1]范围变化的动态条件相关系数转化为处于（-∞，+∞）之间的数值，使之充满整个数轴。并且转换之后的费雪动态条件相关系数具有渐进的标准正态分布性质。费雪转换的公式如下：

FC=0.5Ln（（1+corr）/（1-corr））（5）

转换后的费雪动态条件相关系数的描述性统计如表1所示。

（二）单位根检验

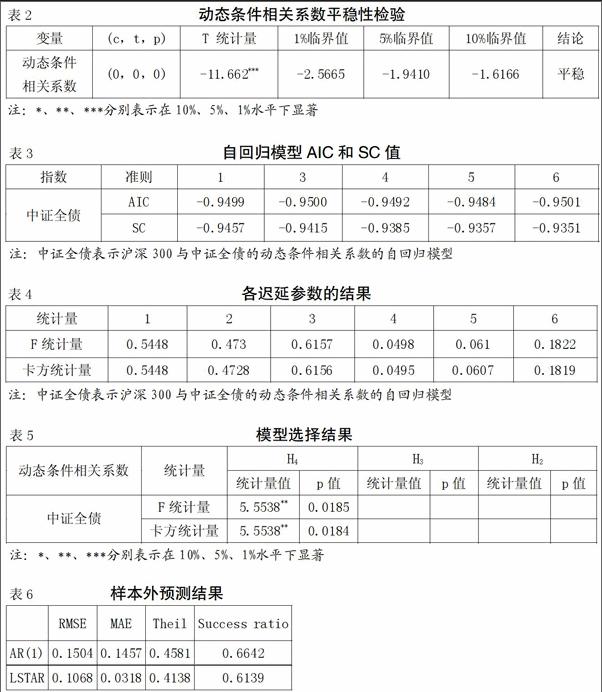
本节仍然采用常用的ADF方法对各个市场的费雪动态条件相关系数进行平稳性检验，结果如下页表2。

从表2可看出，动态条件相关系数都是平稳序列。

（三）滞后阶数的确定

本部分对各个市场的动态条件相关系数建立自回归模型，根据AIC和SC值最小的原则来确定最优的滞后阶数，结果如表3所示。

从表3可看出，对于中证全债的动态条件相关系数，AIC和SC值在1阶自回归时达到最小。

（四）迟延参数的确定

根据本节所阐述的方法，本部分对[1，8]之间的各个迟延参数进行了辅助回归，同时进行了线性检验，结果如表4所示。

从表4可看出，对于中证全债，在5%显著性水平下，只有当迟延参数为4时，F统计量和卡方统计量所对应的P值最小。

（五）非线性模型的选择

在确定了最优的迟延参数后，便可利用前述方法对动态条件相关系数序列做三阶泰勒展开，拟合出辅助回归方程，利用LM方法对原假设进行检验，从而对各个市场的动态条件相关系数在LSTAR和ESTAR模型之间进行选择，检验结果如表5所示。

从表5可知，对于沪深300和中证全债的动态条件相关系数所建立的模型，根据F统计量值和卡方统计量的值及其相应的p值，在显著性水平为5%下，H4被拒绝，因此应该选择LSTAR模型。

（六）样本外预测

如前所述，本部分采用2014年7月1日—2016年9月30日共608个数据进行样本外的预测，以比较自回归模型和平滑转换自回归模型的拟合效果。我们用平均绝对误差（MAE）、均方误差平方根（RMSE）、Theil不相等系数和成功率（SR）这四个指标来评价模型的优劣，Theil不相等系数是RMSE的標量不变版本，其值处于0到1之间，0意味着完全的拟合。成功率是动态条件相关系数符号预测准确所占的比例；RMSE和MAE被用于非线性模型间和非线性与线性模型间的比较。结果如表6所示。

从表6的各项结果可知，非线性模型比自回归模型的预测效果更好，这进一步说明了我国股债动态条件相关系数是非线性的。

四、结论

本文经过单位根检验、自回归模型的滞后阶数的确定、迟延参数的确定、非线性模型的选择和样本外预测等步骤，对我国股债的联动性进行了非线性特征分析，研究发现：沪深300指数与中证全债的联动性呈现非线性，其特征可通过LSTAR模型来刻画。

参考文献：

[1]王俊，孔令夷.非线性时间序列分析STAR模型及其在经济学中的应用[J].数量经济技术经济研究，2006，（1）.

[2]沈春华，许涤龙，路芸.我国通货膨胀率动态波动路径研究——基于LSTR2模型的实证分析[J].华东经济管理，2013，（1）.

[3]谢赤，戴克维，刘潭秋.基于STAR模型的人民币实际汇率行为的描述[J].金融研究，2005，（5）.

[4]张秋莉，杨超，门明.国际碳市场与能源市场动态相依关系研究与启示——基于DCC-MVGARCH模型[J].经济评论，2012，（5）.

[5]赵春艳，韩敏.我国货币供应量与通货膨胀的非线性关系研究——基于LSTR模型的分析[J].财政研究，2014，（6）.

[6]苏非，沈永皎.中国股票市场非线性动态系统风险研究[J].金融经济学研究，2013，28（1）.

[7]谢朝华等.中国股票市场分形与混沌特征：1994-2008[J].系统工程，2010，28（6）.

[8]王成勇，艾春荣.中国经济周期阶段的非线性平滑转换[J].经济研究，2010，（3）.

[9]王晓燕，李美洲.中期和长期国债收益率的非线性协和关系及动态调整[J].金融市场，2012，（2）.

作者简介：

罗荣华，男，北京印刷学院经济管理学院，金融学博士，讲师；研究方向：证券与公司治理。