DNA超分子水凝胶的粗粒化建模与模拟∗

王曦1)2) 黎明1) 叶方富2)1) 周昕1)

1)(中国科学院大学物理科学学院,北京 100049)

2)(中国科学院物理研究所,北京 100190)

1 引 言

超分子水凝胶是一种利用超分子相互作用如氢键、疏水作用等进行交联,形成空间网络的高分子聚合物[1,2].近年来,双链DNA分子因如下原因成为颇受关注的水凝胶材料:较强的机械强度、良好的生物相容、容易通过序列设计对凝胶结构进行调控、DNA链之间的碱基互补配对具有足够的强度和可逆性.纯DNA水凝胶[3−5]和DNA桥接形成的各种凝胶[6,7]成为近年来凝胶领域的重要课题.

迄今为止,文献中已经报道了多种DNA水凝胶[8,9].但对其结构与性能的关系,特别是对凝胶网络的分子化学结构、分子链性质、拓扑孔洞结构、交联密度与强度等结构参数及其与凝胶宏观力学性质之间的关系的了解还十分缺乏,主要是缺少对相应体系的理论建模和实验测量的比较研究[10].因此,构建DNA水凝胶的微观模型并计算模拟其分子结构和宏观性质的功能关系,对理解和设计DNA超分子水凝胶具有重要意义.

DNA水凝胶的宏观性质主要依赖于其分子链段层次的结构与相互作用,其原子尺度的细节及水环境的影响在建立微观模型时需要合理地近似和简化.一般来说,对于DNA分子及其组成的材料,依据系统的大小及特征时间尺度,可采用不同的策略进行建模和模拟[11].当体系大小仅为百碱基对(base pair,bp)量级、所关注的过程在微秒量级及以下时(例如DNA分子自身的形变),可使用全原子模拟[12];当体系大小为千bp、时间尺度为百微秒量级(例如DNA分子与其他生物分子的相互作用),可使用保留一定细节的粗粒化模型,如MARTINI力场下的DNA模型[13];当体系大小超过万bp、时间尺度为亚毫秒及以上量级,则需要使用粗粒化程度更高的模型[14].通常模型中保留的分子细节越多,得到的结果越真实,但所需计算量也越大.对DNA水凝胶等由DNA分子模块组装而成的结构,一般需要忽略大部分DNA分子结构细节,仅保留DNA分子模块的形貌和模块间的相互作用等特征以构建模型,进而计算模拟这些微观特征与组装结构及性能的关系.

本文以文献[15]报道的一种纯DNA自组装水凝胶为例,建立粗粒化模型,模拟研究该DNA水凝胶的分子模块、相互作用等微观特征与凝胶形成、结构及性质的关系,得到了与实验半定量或定性相符的结果.这个工作不仅有助于理解与优化设计该类DNA水凝胶,也为更普遍地构建合理有效的粗粒化模型以研究各种DNA组装体提供了经验.

2 模型与方法

2.1 组装模块的粗粒化模型

目前,Liu等[15,16]设计了可自组装的模块化纯DNA水凝胶.该水凝胶通过预先设计序列的DNA形成小型多分支分子模块,进而使这些分子模块之间通过其末端碱基间的互补配对,自发组装形成空间网络结构.此类水凝胶可以快速自组装,热响应性和酶响应性良好,机械强度较大,在细胞培养、生物学3D打印等领域具有良好的应用前景.我们以此为例,建立粗粒化模型,模拟其微观结构与性能的关系.

该DNA水凝胶由具有三条分支的Y形分子(Y-scaffold)和线状的连接子(linker)构成[15].如图1所示,Y形分子三条臂均为双链DNA,每条臂的末端均有一段单链DNA(ssDNA)作为黏性末端.连接子为线状双链DNA(长约32 bp),两端各有一段ssDNA作为黏性末端.Y形分子和连接子的末端ssDNA序列互补,两者可以自发进行碱基互补配对,形成黏性连接.实验中典型的参数是Y形分子每条双链DNA臂长14 bp,连接子双链DNA长约32 bp,所有ssDNA黏性末端长约8 bp.

由于该DNA水凝胶形成与构象改变对应的较大时间尺度(百微秒毫秒)与空间尺度(亚微米微米),常用的DNA粗粒化模型[17]保留细节较多,导致计算量过大而不适用.为此,我们建立了一个粗粒化程度极高的模型.考虑到Y形分子的分支和连接子的双链DNA段的长度远小于双链DNA的驻留长度(约为50 nm,150 bp),我们将其处理为硬杆.考虑到水凝胶网络的主要相互作用为黏性末端间的连接,我们仅保留这些DNA分子的黏性末端作为粗粒化粒子,其间有相互作用.水凝胶中的水分子被处理为隐性溶剂.最后得到的粗粒化模型如图1所示.

Y形分子粗粒化为由三个粒子(记为A)通过弹簧连接组成的等边三角形,边长为6σ.Y形分子本身可能具有一定程度的形变(例如,三条臂之间夹角的相对变化),这可以近似描述为三角形边长的弹性伸缩.连接子粗粒化为两个粒子(记为B)连接成线状分子,考虑到DNA链的伸缩较小,可视为由硬杆或硬弹簧连接,键长为10σ.键长数值参考实验中的设置,做了较小的近似.σ约为4 bp,更多粗粒化参数设置见后文.

图1 (网刊彩色)粗粒化模型示意图Fig.1.(color online)Schematics of the coarse-grained model

我们分别模拟了粗粒化粒子间键连接为硬弹簧键和硬杆的情况,其中弹簧键的弹性系数为k=0.5ε/σ2,ε为能量参数.模拟表明这两种情况对于感兴趣的物理量,给出的结果基本一致(见附录图A1),因此下文中我们只展示弹簧键的结果.

组成Y形分子的单个粗粒化粒子A,其质量为Y分子单臂质量,约18对碱基质量;组成连接子的单个粗粒化粒子B,其质量为连接子的一半质量,约20对碱基质量.考虑到系统为过阻尼,惯性效应较小,可将A,B分子质量视为相等,均设为m0.

2.2 粗粒化粒子之间的相互作用势

粗粒化粒子为ssDNA构成的黏性末端,粒子间的相互作用为碱基互补配对,具有如下性质:1)不同类型的黏性末端相互吸引配对,同一种黏性末端之间不相互吸引配对;2)一个黏性末端不能同时与多个黏性末端配对,即饱和性.

我们使用Lennard-Jones(LJ)势能[18]作为粗粒化粒子之间的相互作用,对于相互作用的粒子其势能函数为

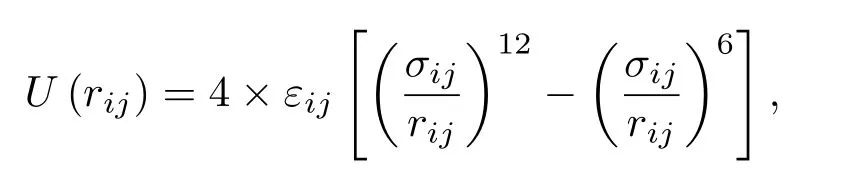
其中,rij为i粒子和j粒子间距,超过截断半径的分子间相互作用力忽略不计;εij和σij表示粒子间的作用势能量和距离参数.粗粒化粒子A,B之间的相互作用势的能量为ε,距离参数为σ,截断距离为2.5σ.这个势能可以在一定程度上模拟两种黏性末端之间的配对和断开.但是,现有的模型难以满足黏性末端的饱和性,需要通过势能设计来实现.

此处的饱和性问题等价于一个A类粒子的力程范围内不能有两个B类粒子同时处于稳态(反之亦然),如图2中的插图所示.

图2 A粒子与其两侧对称分布的两个B粒子组成的三体系统的总势能曲线,本图表明两个B粒子的过饱和态几乎不会出现,插图为A粒子附近两个B粒子处于过饱和状态时的示意图Fig.2.Total potential energy of the three-body system consisting of an A particle and two B particles which are placed symmetrically around A.This graph indicates that the over-saturated state can hardly occur.Small f i gure shows schematics of two B particles simultaneously interacting with an A particle and forming an over-saturated state.

为了实现饱和性,我们引入了同种粒子间的LJ排斥势,通过较大范围的排斥使得同种粒子难以同时存在于一个较小的区域.排斥势也同时实现了同种黏性末端不相互吸引配对的特性.此处我们设置同种粒子之间相互作用势的能量为ε,距离参数为4σ,截断距离为势能极小值点,约为4.49σ,同时将势能函数进行向上平移修正,使其在截断点处的势能为0.

假设该三体系统能够处于稳态,则根据对称性,两个B粒子与A粒子距离相等.总势能为

UBB为排斥势,随rBB增大而减小,则θ=180°时Utotal最小,此时Utotal随rAB的分布曲线如图2所示,极小值点能量约为−0.03ε.而模拟中的最低温度为0.04T0=0.04ε/kB,此时热涨落能量大于稳态势阱深度.因此,在模拟温度范围内(T=0.04T0—0.30T0),该三体态非常不稳定,极易受热涨落破坏.经统计,在实际模拟过程中,过饱和的键占整个系统的比例小于0.01%,如附录图A2所示,证明我们的模型在饱和性方面是非常有效的.

2.3 粗粒化参数的真实单位对应

粗粒化模型的长度单位σ、质量单位m0等基本来源于实验中的DNA参数,为了模型的简化进行了部分微调.

粗粒化温度单位由能量标定,即T0=ε/kB.例如文献[15]实验中使用的标准8 bp长度黏性末端,根据其DNA序列,由Santalucia近邻热力学参数[19],可以近似估计300 K温度(即室温Tr)下黏性末端配对的自由能ε约为10kBTr—16kBTr,实际数值受浓度、离子环境等因素影响而波动.即对应于此8 bp黏性末端,其真实温度300 K对应于粗粒化温度T=0.06T00.1T0.模型参数及其赋值列于表1.

表1 模型参数及其赋值Table 1.List of the model parameters and their values.

所有分子动力学模拟都采用LAMMPS软件通过粗粒化力场进行模拟.模拟过程主要使用Langevin动力学[20].模拟体系采用周期性边界条件,主要采用边长为100σ的立方体盒子,部分模拟使用八倍、十六倍等体积的盒子.Y形分子与连接子数量比例为1:1.5以保持两者黏性末端总数量相等,从而达到较高的配对效率,该比例与实验相符[15].粗粒化粒子数从900至14400不等,由系统大小和粒子数密度决定,粗粒化系统粒子数密度与实验中的真实浓度对比见表2.模拟温度范围为0.04T0—0.30T0.模拟步长为0.005t,温度阻尼系数为0.5t.单个模拟轨道时长为1亿步至10亿步.

表2 粒子数密度与真实Y形分子浓度对比(密度单位:个/(100σ)3)Table 2.Correspondence between the concentration of the coarse-grained particles and the concentration of Y-scaffold blocks used in experiments.

3 结果与讨论

3.1 二维体系

二维情况下的模拟对于了解体系结构与性质具有一定参考价值.我们模拟了边长为400σ的正方形二维盒子,粒子数为2880.

模拟发现,在多个温度模拟下,二维水凝胶体系呈现出两种不同的状态.如附录图A3所示,低温态(T=0.06)粒子分布不均匀,出现粒子聚集和较大空隙,处于聚集态;高温态(T=0.20)粒子分布较均匀,处于液态.

图3 (网刊彩色)平均势能与Y分子平均配对数随温度的变化Fig.3.(color online)Average potential energy and pair number per Y-scaffold at different temperatures.

为了更精确地描述该系统的凝胶化程度,我们引入Y分子的平均配对数作为序参量以描述系统的交联度.Y分子含三个黏性末端,其最高配对数为三,而连接子与Y分子的总黏性末端数相等,因此Y分子平均配对数越接近三,系统交联度越高,其凝胶化程度越高.

低温聚集态和高温液态对应的势能曲线和Y分子平均配对数曲线如图3所示.随着温度上升,体系的平均势能上升,Y分子平均配对数下降.

3.2 三维体系

如图4所示,与二维情况类似,粗粒化模拟体系在低温(T≤0.06T0)下形成多孔海绵状结构,几乎所有分子都处于交联网络中.

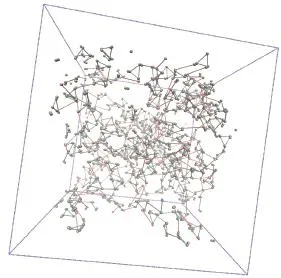
图4 (网刊彩色)三维水凝胶体系模拟结构图Fig.4.(color online)Structure of simulated threedimensional hydrogel system.

3.2.1 势能与交联密度

如图5所示,随着温度上升,体系的平均势能上升,平均配对数下降,且低温下近饱和,这与二维体系一致.说明系统存在两个可能的状态,低温下凝胶化程度高,高温下程度低.升降温曲线的重合表明系统随温度的转变没有通常结晶与熔化过程中的热滞现象.

为了考察上述结果是否依赖于模拟体系的大小,我们对密度同样为200µM的不同体积的系统进行了模拟,得到其平均配对数如图6所示.可以看出,不同体积下平均配对数曲线基本重合,没有显示出有限尺度效应,说明我们的模拟结果的确可以反映出宏观体系的特征.

图5 (网刊彩色)势能与平均配对数曲线与温度的关系Fig.5.(color online)Average potential energy and pair number per Y-scaffold at different temperatures.

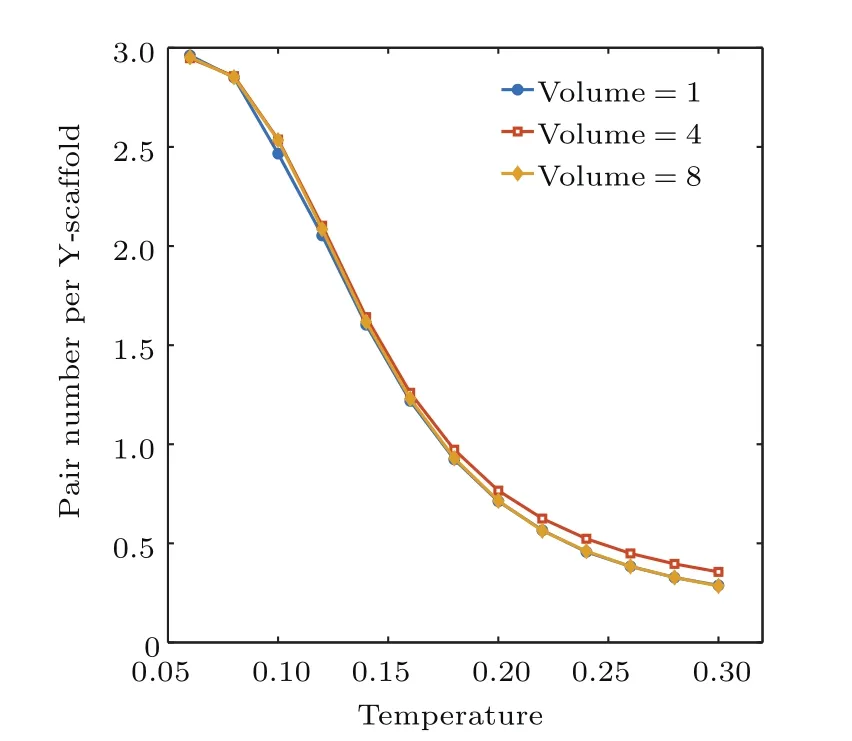
图6 (网刊彩色)相同密度、不同体积的系统中平均配对数与温度的关系Fig.6.(color online)Pair number per Y-scaffold of systems with different sizes and the same density.

3.2.2 扩散行为

为了进一步描述系统在两种状态下的性质,我们考察了粗粒化粒子扩散行为的转变.均方位移(msd)是描述系统扩散性质的物理量.其定义为

一般msd满足:

通常α＜1对应于次扩散(sub-diffusion),α＞1对应于超扩散(super-diffusion),而α=1对应于正常扩散.

我们对不同温度下系统的msd进行计算,并在双对数坐标下进行拟合,拟合得到直线斜率即为α.拟合时主要取msd曲线后半段,粒子扩散达到稳态的区域,大致为后50%的数据点,在双对数坐标下对应于大约t＞105之后的曲线.双对数坐标下的msd曲线如图7所示.

图7 (网刊彩色)系统msd随时间变化的曲线(双对数坐标),图中两条虚线斜率为1Fig.7.(color online)The mean squared displacement of the system as a function of time t under different temperatures(in double logarithmic coordinates).The slope of each dashed line is 1.

从图7可以看到,高温(T≥0.10T0)下系统的msd曲线基本平行,斜率接近1,说明此时为常规扩散,表明系统为液态;低温(T≤0.06T0)下系统的msd曲线拟合直线斜率明显小于1,表明系统处于凝胶态,扩散受到限制.

3.2.3 Voronoi单胞与局域密度分布

为了进一步研究这个粗粒化系统的微观结构,我们以粗粒化粒子的位置为种子点计算了该系统的Voronoi单胞的体积分布.Voronoi图是一种基于距离的空间划分方法[21,22],该方法将空间划分为若干区域,使得每个区域内的点距其种子点的距离比其他种子点更近,每个区域为一个Voronoi单胞.Voronoi单胞的体积大小反映了种子点的局域密度分布.

如图8所示,随着温度下降,Voronoi单胞体积分布曲线的峰左移且升高.同时,在平均体积线右侧(V=1100—2000位置),分布曲线升高.这表明在低温下,系统中大量粒子集中于高密度态,同时还有相当一部分粒子处于低密度态,形成了海绵状结构.而高温下体积分布趋于平均线,大体积单胞也较少.表明高温下系统结构较为平均,接近液态.

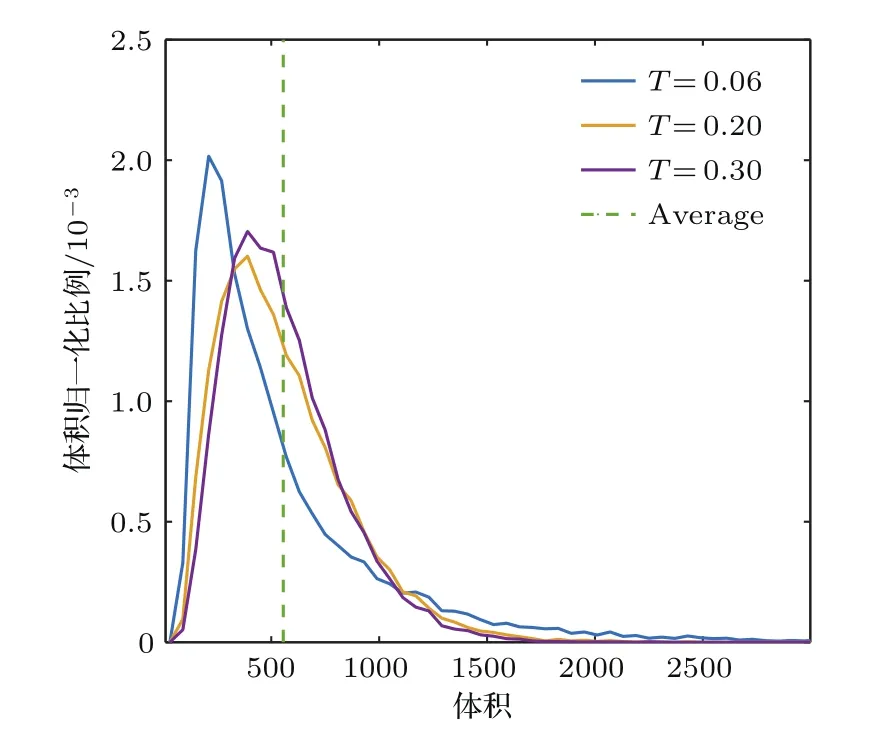
图8 (网刊彩色)Voronoi单胞体积分布(归一化)Fig.8.(color online)Volume distribution of Voronoi cells

Voronoi单胞体积也可以用于描述凝胶中的孔洞尺寸,可以大致预测凝胶中的孔洞体积约为10000σ3—100000σ3(对应于实际尺寸约为30000—300000 nm3),将来或可与实验测出的数值进行半定量对比验证.

3.2.4 密度的影响

为了与实验[15]进行对比,我们也研究了粒子密度对体系凝胶化程度的影响.在实验中,DNA水凝胶模块的浓度增加会使体系储能模量增大,对应着凝胶化程度的增加.

图9 (网刊彩色)不同模块密度下平均配对数随温度的变化Fig.9.(color online)Pair number per Y-scaffold at different temperatures for systems with different densities.

我们的模拟结果如图9所示,平均配对数与密度成正相关.相同温度下,高密度系统其交联程度更高,更容易凝胶化.温度足够低时,四条曲线基本归于一点,系统的平均配对数基本饱和.这与实验结果相符合.

3.3 微流变与力学性质

为了进一步研究系统的流变学性质,我们使用微流变学[23,24]方法对该系统进行研究.微流变学方法通过在系统中加入少量示踪粒子,探测示踪粒子的msd等参量,进而得到系统的一些性质.

此处我们使用的示踪粒子为单个粗粒化粒子B,即组成连接子的粗粒化粒子.分别在不同的温度和不同大小的拉力下进行了模拟.

3.3.1 不同温度下的被动微流变

被动微流变[25]中,对于示踪粒子不施加外力.对于不同温度下的系统进行多组模拟(每个条件下100条轨道),并对示踪粒子进行了轨道平均.最终求出粒子的msd与时间的关系,如图10所示.此外,我们仍按照前述方法,取后50%(即t＞105的稳态区域)的数据点进行拟合,求出各线性区对应的指数α,得到其随温度的变化,如图10中的插图所示.

图10 (网刊彩色)示踪粒子的msd随时间变化(双对数坐标),图中两条虚线斜率为1,插图为指数α与温度的关系Fig.10.(color online)The mean squared displacement of the tracer as a function of time.The slope of each dashed line is 1.Small f i gure shows α for different temperatures

从图10可以看到T≤0.08T0时曲线斜率α小于1,为次扩散,系统处于凝胶态;T≥0.10T0时,曲线斜率α在1附近,为常规扩散,系统处于液态.这表明系统的凝胶液态转变温度在0.06T0—0.10T0之间,与上文系统整体msd的结果大致符合.

3.3.2 不同拉力下的主动微流变

主动微流变[26]中,对于示踪粒子施加外力以观察其轨迹.示踪粒子在拉力方向上的msd为

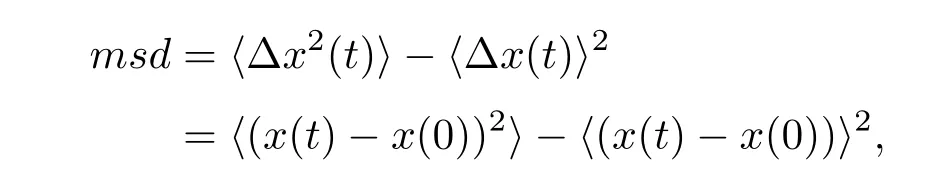
其中〈Δx2(t)〉=〈(x(t)−x(0))〉2为通常定义中的msd,表征粒子的扩散作用.但是此处的Δx(t)不仅包含粒子扩散,还包含拉力导致的相对t=0时的粒子移动.为了去除这一影响,需进行一个修正,减去〈Δx(t)〉2=〈(x(t)−x(0))〉2这一由外力拖拽造成的粒子偏移.

我们在示踪粒子上加上一个x方向的牵引力,计算其牵引方向的msd,以探究其在非平衡状态下的力学性质.此处我们先对每条轨道进行了窗口平均计算得出各自的msd,再进行轨道平均,得到如图11所示的双对数坐标下的msd.由图11可以发现,在较长的关联时间下,随着外力的增加,msd曲线表现出超线性行为.对长关联时间下的区域即msd的后半段(t＞103.5)进行拟合,得到扩散指数α随温度的变化如图11中的插图所示.

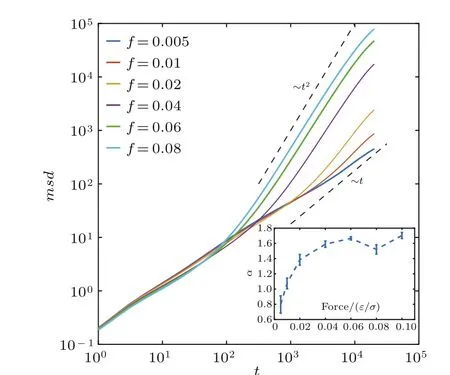
图11 (网刊彩色)示踪粒子在力方向上的msd随时间变化(双对数坐标),插图为指数α与外力的关系Fig.11.(color online)The mean squared displacement in the force direction of the tracer as a function of time.Small f i gure shows α for different forces.

由图11可以看到,F≤ 0.005ε/σ时,α ＜1,示踪粒子近似表现为扩散行为;F≥0.02ε/σ时,α＞1,示踪粒子表现为超扩散.这表明示踪粒子的外力增加到一个值(0.02ε/σ)时,会很快由扩散行为变为近似匀速运动.外力导致的示踪粒子扩散超扩散转变的临界力在0.005ε/σ—0.02ε/σ之间.

3.4 与实验的半定量对比

本文的粗粒化模型预言体系发生“凝胶-液态”转变的温度区间大致为

在黏性末端长度变化范围较小的情况下,该模型对应的水凝胶的转变温度正比于黏性末端结合能.因此我们可以根据黏性末端的DNA序列预测水凝胶真实的“凝胶-溶液态”转变温度.

例如,对于文献[15]实验中采用的标准8 bp黏性末端,其结合能约为10kBTr—16kBTr,粗粒化温度0.06T0—0.10T0对应的真实温度约为300 K.而根据文献[15]图2(d)的结果,该DNA水凝胶的凝胶溶液态转变温度在25—50°C范围,即298—323 K内.模拟与实验基本符合.

文献[15]的图3比较了多组黏性末端的转变温度,表明黏性末端结合能越高,其转变温度越高.这与我们的结论一致.

转变温度与黏性末端结合能的关系可以对DNA水凝胶序列设计提供一定的指导.例如,对于模型对应的长度范围内的DNA水凝胶,为了使其在300 K下成胶,其结合能不能低于10kBTr—12.5kBTr.

另外,根据我们的模拟,DNA水凝胶浓度越高,则相同温度下其交联程度越高,凝胶化程度越大.在文献[15]图S2中,水凝胶储能模量随浓度增加而增大,同样表明凝胶化程度与浓度成正相关.本文模拟与实验在定性上一致.

根据凝胶-液态转变温度范围,我们可以推测出该DNA水凝胶成胶的交联度条件大致为Y分子平均配对数大于2.7,即90%以上的黏性末端处于配对交联状态.因此对于不同浓度下的水凝胶,可以通过交联度预测其成胶温度.这将来或可与实验测出的数值进行半定量对比验证.

4 结 论

我们设计了一种适用于DNA水凝胶的粗粒化模型,并针对一种DNA水凝胶进行了分子动力学模拟验证.该模型对凝胶分子模块进行了极大的简化以减少计算量,并通过LJ排斥势的设计实现了DNA配对的饱和性.

针对该DNA水凝胶的模拟结果发现,该系统在不同温度下存在较均匀的液体态和海绵状的凝胶态两种状态.两种状态间随温度改变发生连续转变,且转变受密度因素影响.我们深入研究了两种状态下系统的结构和扩散性质,并做出了结构上的预测.此外,通过微流变方法进一步得出系统的两态转变温度约为0.06ε/kB—0.10ε/kB,并与文献[15]中的一些结果进行对照,两者基本一致.这一转变温度与黏性末端结合能的关系,可以对DNA水凝胶的设计和转变温度控制提供一定的指导.

另外,我们也预测该水凝胶成胶条件为黏性末端配对交联比例大致超过90%.外力引起的粒子扩散超扩散转变的临界力范围为0.005ε/σ—0.02ε/σ.

基于该粗粒化模型进行模拟的结果与合作组的实验结果基本相符,证明此模型对DNA水凝胶的模拟较为合理.对于更多类型的DNA水凝胶,或使用DNA链作为连接基团的胶体系统,该模型由于其计算量小又满足饱和性等优势,在模拟上具有潜在的应用前景.

附录A

A1弹簧键和硬杆的对比

在模拟中,弹簧键使用谐振势,为

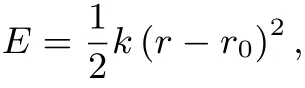
其中r0为平衡位置距离,k为弹性系数.对于线状连接子,弹簧键对应的是线状双链DNA的伸缩与弯曲造成的黏性末端之间距离的变化.本文所研究的双链DNA长度远小于其驻留长度,其伸缩和弯曲较小,可视为硬杆,故而连接子使用弹性系数较大的弹簧键,弹性系数k=0.5ε/σ2.对于Y形分子,弹簧键(键长为6σ)对应的是Y分子自身形变造成的黏性末端间的距离变化,主要来源为三条刚性臂间夹角在120°附近的较小变化.因此,同一个Y分子中的两个A粒子之间的距离应该小于Y分子臂长的两倍(约6.93σ),而且不会过于靠近.实际上,在我们的模型中,为了满足黏性末端相互作用的饱和性,在组成Y分子的粗粒化粒子A之间具有较长距离的排斥势(作用范围4.49σ),这实际使得同一个Y分子中的两个A粒子之间的距离也通常大于这个排斥势范围.因此弹簧键长变化范围约为4.49σ—6.93σ,实际效果接近硬弹簧,因此我们采用较大的弹性系数,弹性系数k=0.5ε/σ2.

对于分子键为硬杆的模型,在Lammps软件模拟中,为了实现键长不变,需要通过shake算法[27]对键长进行约束.该算法通过每一步对原子施加附加约束力,通过迭代计算使键长重置为平衡长度.

我们在弹簧和硬杆两种模型下分别进行了模拟,得到在(100σ)3大小,总粒子数为1800的NVT系统中,Y分子平均配对数随温度分布曲线,为了进行对比,我们同时模拟了Y分子的弹簧键分别为硬弹簧(k=0.5ε/σ2)和软弹簧(k=0.05ε/σ2)时的情况作为参考,模拟结果如图A1所示.

图A1 (网刊彩色)分子键为硬弹簧(k=0.5)、软弹簧(k=0.05)和硬杆三种情况下Y分子平均配对数与温度的关系(误差棒为标准误差)Fig.A1.(color online)Pair number per Y-scaffold at different temperatures,simulated by hard spring model(k=0.5),soft spring model(k=0.05)or stiffstick model

可以看到,硬杆和硬弹簧两种分子键下,Y分子平均配对数基本重合,这表明硬弹簧和硬杆在系统交联度等结构方面的影响基本相同.软弹簧在低温下Y分子平均配对数小于另外两种模型.在实际模拟中,也多次出现弹簧键长过长的情况,偏离了实际系统.可以认为弹性系数较小的软弹簧模型不适合当前DNA水凝胶系统,因此只采用硬弹簧和硬杆的结果.

A2过饱和概率统计

我们统计了系统在多个温度下过饱和配对数占单种黏性末端总数的比例,每个温度下统计2000帧,平均后得到过饱和比例如图A2所示.

可以看到,在模拟的温度范围内,过饱和比例均小于0.01%.考虑到我们模拟的系统最大粒子数只有一万至二万,大部分模拟中粒子数不足一万,可以认为我们的模型基本满足了DNA链配对的饱和性.

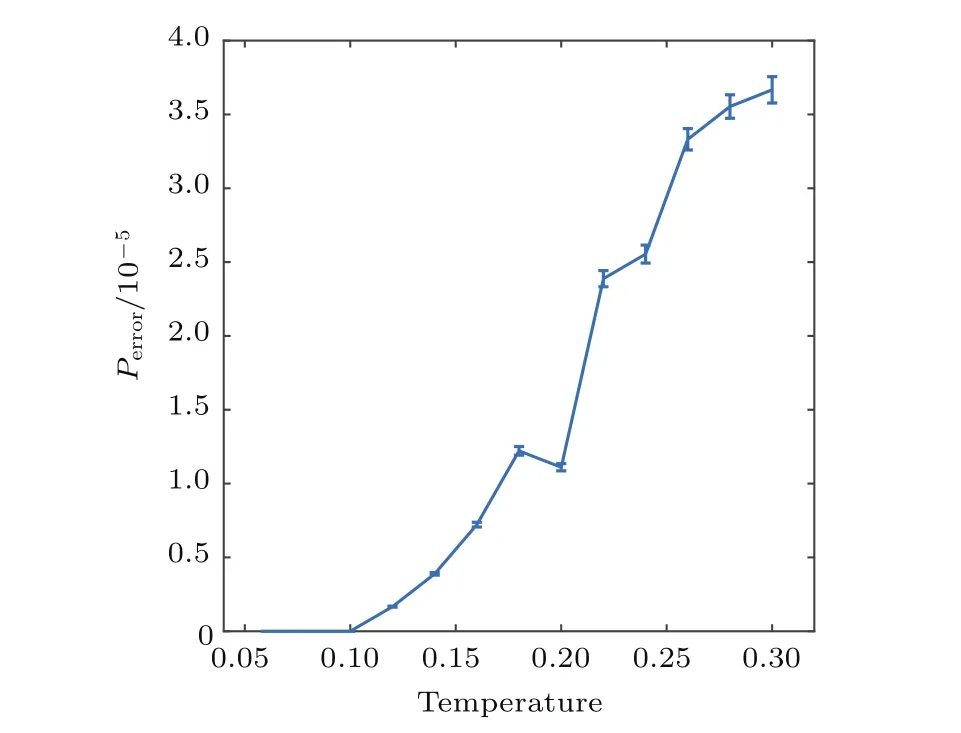
图A2 不同温度下的过饱和比例(误差棒为标准误差)Fig.A2.The ratio of over-saturated pairs at different temperatures.

A3二维系统低温与高温态构象

模拟得到的二维系统构象如图A3所示,可以看到低温下大多数分子都处于连接状态,且单个Y分子所连接的连接子数目大多为2或3,出现分子聚集,系统形成密度不均匀的分布.高温下,存在大量Y分子其相连的连接子数目小于2,系统形成密度较均匀的分布.

因为模型中不考虑DNA链的排斥体积,二维情况下可能存在少量键交叠的现象,而在三维情况下基本不会发生交叠.本文主要研究三维体系,因此不进一步考虑键交叠的影响.

[1]Foster J A,Steed J W 2010Angew.Chem.Int.Ed.49 6718

[2]Yu G,Yan X,Han C,Huang F 2013Chem.Soc.Rev.42 6697

[3]Topuz F,Okay O 2008Macromolecules41 8847

[4]Morán M C,Miguel M G,Lindman B 2010Soft Matter6 3143

[5]Um S H,Lee J B,Park N,Kwon S Y,Umbach C C,Luo D 2006Nat.Mater.5 797

[6]Angioletti-Uberti S,Mognetti B M,Frenkel D 2016PCCP18 6373

[7]Li C,Faulkner-Jones A,Dun A R,Jin J,Chen P,Xing Y,Yang Z,Li Z,Shu W,Liu D,Duncan R R 2015Angew.Chem.Int.Ed.54 3957

[8]Amiya T,Tanaka T 1987Macromolecules20 1162

[9]Topuz F,Okay O 2009Biomacromolecules10 2652

[10]Starr F W,Sciortino F 2006J.Phys.:Condens.Mater.18 L347

[11]Dans P D,Walther J,Gómez H,Orozco M 2016Curr.Opin.Struct.Biol.37 29

[12]Weiner S J,Kollman P A,Nguyen D T,Case D A 1986J.Comput.Chem.7 230

[13]Uusitalo J J,Ingólfsson H I,Akhshi P,Tieleman D P,Marrink S J 2015J.Chem.Theory Comput.11 3932

[14]Collepardo-Guevara R,Schlick T 2014Proc.Natl.Acad.Sci.USA111 8061

[15]Xing Y,Cheng E,Yang Y,Chen P,Zhang T,Sun Y,Yang Z,Liu D 2011Adv.Mater.23 1117

[16]Cheng E,Xing Y,Chen P,Yang Y,Sun Y,Zhou D,Xu L,Fan Q,Liu D 2009Angew.Chem.121 7796

[17]Ouldridge T E,Louis A A,Doye J P K 2010Phys.Rev.Lett.104 178101

[18]Lennard-Jones J E 1931Proc.Phys.Soc.43 461

[19]SantaLucia J 1998Proc.Natl.Acad.Sci.USA95 1460

[20]Schneider T,Stoll E 1978Phys.Rev.B17 1302

[21]Okabe A 1992Spatial Tessellations(New York:John Wiley&Sons)pp362–363

[22]Aurenhammer F 1991ACM Comput.Surv.23 345

[23]Winter D,Horbach J 2013J.Chem.Phys.138 12A512

[24]Mason T G,Weitz D 1995Phys.Rev.Lett.74 1250

[25]Mizuno D,Head D A 2008Macromolecules41 7194

[26]Choi S Q,Steltenkamp S,Zasadzinski J A,Squires T M 2011Nat.Commun.2 312

[27]Ryckaert J P,Ciccotti G,Berendsen H J C 1977J.Comput.Phys.23 327