大气损耗对量子干涉雷达的影响机理∗

2017-04-26 09:21王书任益充饶瑞中苗锡奎

物理学报 2017年15期

关键词：光场损耗分辨率

王书任益充饶瑞中苗锡奎

1)(中国科学院安徽光学精密机械研究所,中国科学院大气成分与光学重点实验室,合肥 230031)

2)(中国科学技术大学,合肥 230026)

3)(光电对抗测试评估技术重点实验室,洛阳 471003)

1 引言

雷达是用于远距离目标探测及测距的传感设备,通过发射电磁波并接收目标反射的回波信号来探测目标距离、速度、形状等,在军事领域有着非常广泛的应用.随着雷达技术的进步,雷达系统从单纯利用信号的强度信息演化为对信号频率和相位信息的综合利用,有效提升了雷达的抗干扰、抗杂波能力;电子干扰技术的进一步发展以及隐身战机的出现,对现有的雷达体系提出了进一步的挑战;传统雷达受限于经典的电磁理论,其在提高灵敏度探测隐身目标,提高成像分辨率、抗电磁干扰等方面均遇到难以突破的瓶颈,已无法满足日益苛刻的军事和国防需求[1].为应对隐身战机和电子干扰技术的挑战、突破经典电磁理论下雷达灵敏度、分辨率极限,须引入量子理论以彻底打破经典电磁理论的桎梏[2];量子雷达将量子光学和量子信息技术引入雷达探测领域,从量子角度对接收机噪声、散粒噪声等给予全新的解释,并以此为基础从调制载体和检测处理等方面入手,全面提升雷达性能[3].利用量子态的信号以及光量子测量技术,量子雷达具有传统雷达难以比拟的优势.

1)超灵敏度:基于量子原理和全新检测手段的量子雷达能够降低噪声并利用量子关联特性从噪声中检测出微弱的信号,因此量子雷达能够突破标准量子极限(散粒噪声极限),具有超灵敏度特性[4].

2)超分辨率:量子雷达的目标探测分辨率能够突破经典的瑞利衍射极限O(λ),最高可分辨率可提高N倍达到O(λ/N)级别,故量子雷达能够在不改变信号波长的情况下通过调节信号强度来提高分辨率[5].

3)散射截面:量子雷达可使用少数光子甚至单光子作为信号对目标进行探测,研究表明目标物体的单光子散射截面大于其经典散射截面,即使用量子雷达时目标的散射截面更大[6].

4)功耗与体积:量子雷达的超分辨率使得其无需通过增大接收口径、合成孔径等方案来提高分辨率,超灵敏优势意味着其在较低功耗下即可实现相对较高的信噪比,因此量子雷达在功耗和体积上拥有经典雷达无法比拟的优势.

鉴于以上诸多优点,未来量子雷达将在军事领域、工程测绘、空间探测、空天对抗等有着重要的应用:如量子雷达凭借超分辨率、超灵敏度等优势能够用于探测隐身目标、雷达成像、抗干扰欺骗等,还可用于探测近地空间中高速运行的陨石或卫星碎片等;未来装备量子雷达的战机能够在数千公里外发现、锁定地方目标,并利用配备的导弹对敌发起攻击,这将大大削弱航空母舰作为空中打击平台的地位,并彻底改变未来的空战模式;此外,量子雷达的研发需要雷达波段的激光光源及相应频段的探测器等,这些技术在其他领域如量子通信、量子计算等均有着非常重要的作用.

量子雷达的理论和原理性论证起步较早,Bakut在1966年首先讨论雷达系统中使用量子信号的可行性[7];随后在二十世纪七八十年代,量子最优接收机的研究相继展开,建立了量子测量与估计理论(quantum detection and estimation theory)[8],并不断涌现出突破标准量子极限的进展.进入二十世纪九十年代后,Jehle和Hudson[9]着手研究雷达系统中的量子探测问题,并催生了量子测距、量子同步、量子传感和量子成像等诸多新兴研究领域.

21世纪初,中国、俄罗斯等先后开展了隐身战机的研发,尤其我国对J20和J31隐身战机的研发,促使美国投入资源研发量子雷达.美国防部高级研究计划局(DAPRA)先后启动量子传感(Quantum Sennsor Program,2007)、量子激光雷达(Quantum Lidar,2007)、单光子信息技术(Information in a Photon,2009)等项目,标志着量子雷达研究领域的正式形成.以麻省理工大学、西北大学、德州大学、雷神BBN公司、哈里斯公司等研究团队为代表的研究人员针对量子雷达的具体实现提出了多种方案,主要可分为干涉式量子雷达(interferometric quantum radar)、接收端量子增强雷达(quantum enhanced lidar)、量子照明(quantum illumination)三种方案[10−12].这三种不同类型的量子雷达方案有着不同的特点:

1)量子照明雷达结构简单,其灵敏度可达到海森伯极限O(1/N),但其不具备超分辨率特点,且需知道目标的大致距离方可进行符合测量,故必须与其他雷达配合使用,这就大大局限了其应用范围[13,14];此外,为达到更高的灵敏度需要使用粒子数N更大的纠缠态,然而这种纠缠态的实验室产生也比较困难,因此量子照明雷达的初步实现难度较小,但进一步的提升相对困难[15];

2)量子增强雷达发射端与普通激光雷达完全相同,其仅在接收端采用了量子增强技术,故该方案能够通过对激光雷达的改装实现,且在雷达测距、激光成像等方面都有着重要的应用,但其对雷达分辨率、灵敏度等性能的提升存在很大的限制[10,11,16,17];

3)干涉式量子雷达结构相对复杂,但其具备超灵敏度、超分辨率的双重优势,例如采用纠缠相干态、压缩态光源时,其灵敏度可突破标准量子极限达到O(λ)级别的海森伯极限,其分辨率最高可达O(λ/N)级别;此外,干涉式量子雷达的光源调制、干涉方案、信号检测等都有着众多的设计方案,例如其既可采用Fock态、纠缠态、相干纠缠态、压缩态、M&M′态等非经典光源,亦可采用相干态光源;干涉式量子雷达的测距原理是基于对回波信号的相位检测,故其拥有其他方案所没有的超分辨率优势[18−20].

未来成熟的、实用化的量子雷达将采用雷达频段的激光光源,此时采用干涉式方案的量子雷达在分辨率上就拥有着其他方案无可比拟的优势(目前的量子雷达在原理验证阶段多采用常见激光波段如780,1550 nm等,此时激光波长λ非常短,即使在衍射极限下其分辨率可达微米量级,此时作为测距的精度已足够.但若采用厘米波、分米波、米波频段的光源,则干涉式量子雷达的O(λ/N)级别的超分辨率优势非常明显).本文选择干涉式量子雷达作为研究重点,首先针对其进行建模,给出干涉式量子雷达的物理模型;随后对采用相干态光源时的雷达性能及大气损耗的影响等展开进一步的研究.本文第2部分介绍量子干涉雷达的基本结构并引入相应的算符以及Su(2)李群,用于描述光场通过分束器及其相移过程等;第3部分建立干涉式量子雷达的量子模型,并对光场的演化等进行计算;第4部分介绍相位检测的原理并采用宇称算符Π=eiπa†a作为检测方案;第5部分详细分析大气损耗对干涉式量子雷达分辨率、灵敏度的影响,并提出了改进的方法等;第6部分是对本文的总结及未来进一步的工作展望等.

2 量子干涉雷达结构及物理模型

图1为采用相干态光源的量子干涉雷达结构示意图,其中CRS为相干激光光源,QHD为信号探测系统.激光信号在发射端CRS处由分束器变为两束,其中一束留在本地作为参考光(图中用红色示意),另一束则作为探测光发射出去用于对目标区域的扫描(图中用蓝色示意).由于两束光的光程不同,会产生一定的相位差,随后将接受到的探测光与参考光在分束器上重新干涉,并用量子光学的方法对其进行相干检测即可测得此相位差,从而能够探测得到目标的距离信息.从图1可以看出,干涉式量子雷达的核心干涉结构类似于马赫-曾德尔干涉仪(Mach-Zehnder interferometric,MZI),因此能够利用MZI模型对其进行描述.

图1 (网刊彩色)相干态光源的双模量子干涉雷达模型Fig.1.(color online)The physical model of two-mode interferometric quantum radar with coherent-states sources.

文献[21,22]指出干涉仪具有Su(2)或Su(1,1)的李群结构,并给出了相应的幺正算符用于描述光场在干涉仪中的演化过程;分束器(beam splitter,BS)是干涉仪中的重要部件,首先应考虑分束器所对应的幺正算符,其原理如图2所示.

图2中左侧Ain,Bin分别代表输入光场,右侧Aout,Bout为输出光场,输入和输出光场的湮灭算符分别表示为ain,bin与aout,bout,它们之间一般有如下关系:

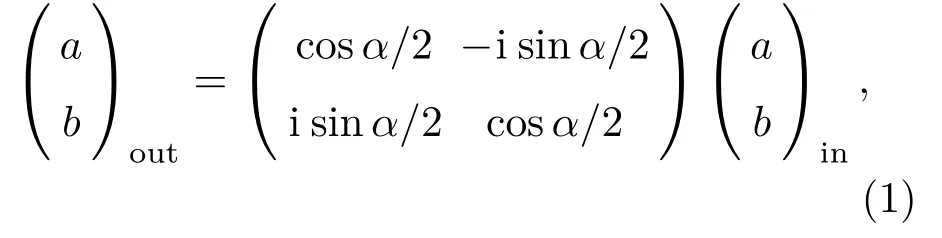
其中cos2α/2,sin2α/2分别代表分束器的反射率和透射率.注意到(1)式代表转动变换,而所有转动变换都可用Su(2)群来描述,故依据文献[21,23]针对双模光场a和b定义如下算符:

容易验证幺正算符U(α)=exp{−iαJx}满足(1)式所代表的变换,即

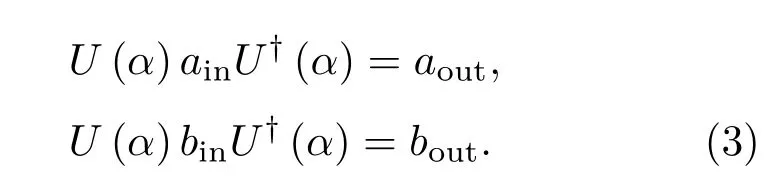
因此光场量子态|ψin〉经过分束器后则变为

若忽略分束器反射和透射引起的相差,则光通过分束器后的光场算符变换关系为

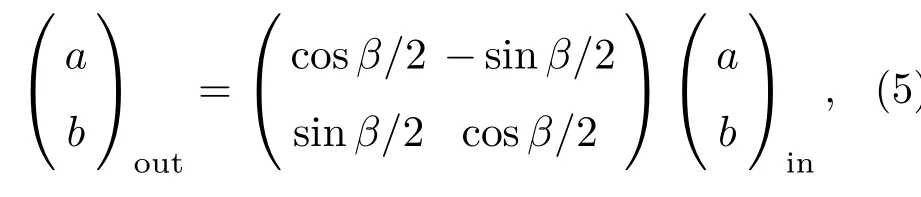
此时描述上述变换的幺正算符为

Jx,Jy可描述分束器变换,Jz可用于描述光场的相移,即幺正算符Uz=ei(γ2−γ1)Jz可描述如下变换:

综上所述,Ux,Uy可代表不同类型的分束器所产生的幺正变换,而Uz则可描述光场在传输过程中出现相移的过程,这三个幺正算符将会被应用于对量子雷达的模型分析中.

图2 (网刊彩色)分束器的分光模型Fig.2.(color online)The physical model of beam splitter.

3 量子干涉雷达目标探测原理

由图1量子干涉雷达的结构示意图,可以看出量子干涉雷达的核心干涉部件为MZI,因此可利用MZI模型对量子干涉雷达的目标探测原理进行深入分析.基于相干态的量子干涉雷达的物理模型如图3所示.

图3 (网刊彩色)量子干涉雷达的MZI模型示意图Fig.3.(color online)The diagram of the MZI model of quantum interferometric radar.

图3 中BS1/BS2代表50:50的分束器,从左侧Ain端输入相干态|α〉,Bin端输入真空态|0〉光场,在BS1上产生干涉,而后将其中上面一路光作为探测光用于扫描目标区域,下面一路光留在本地作为参考光;由于参考光与探测光的光程差不同,两者间产生大小为φ的相位差;在传输过程中,参考光与探测光均有一定程度的损耗,τA,τB分别代表两束光的衰减系数;随后反射回来的探测光与参考光在分束器BS2上再次干涉后,在Aout端或Bout端对信号进行检测即可得到关于相位φ的信息,进而可测得到目标的距离.

需要指出的是,量子干涉雷达在真实的目标探测过程中,其探测光和参考光的光程差可能高达几百公里,当光程差远大于激光的相干长度时,BS2处参考光与探测光的干涉效率极低,使得无法进行目标探测;此外,量子干涉雷达系统一般使用脉冲信号对远程目标进行探测,通过脉冲信号的往返时间推算得到目标距离,而后通过相位估计可得到更加精确的目标距离.然而当参考光与目标光光程差过大时,会导致两束光在不同时间到达分束器BS2.为解决此问题,无论是量子照射雷达还是量子干涉雷达都需要对参考光加装延迟线,即延时光纤,如图1中左下角所示的延迟线,延时光纤能够增大参考光的光程并减小两束光的光程差,从而解决时间延迟问题.本小节主要研究量子干涉雷达的探测原理及性能分析,延时线的作用主要在于保证参考光与探测光的探测效率,故在图3中无需再额外考虑两束光之间的时间延迟问题.

若左侧双模输入光场A,B密度算符为ρin,则在II处双模光场经过分束器BS1与相移φ后,密度算符变为

随后ρ2经过大气通道的衰减后变为ρ3,此衰减过程可用耗散通道的主方程来描述[22,24]:

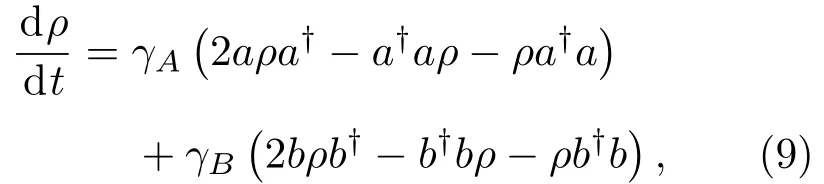
式中γA,γB分别代表A,B的自发辐射速率;类似(9)式的单模光场的耗散主方程已被各种方法求解[22−25].我们进一步将单模光场耗散主方程的Kraus算符解推广到双模光场情况(文献[25]中求解了单模光场的情况,而本文进一步考虑了双模光场的情况,由于A,B两模光场之间并无相互作用,所以只需要将文献[25]中的单模Kraus求解进行扩充即可求得双模情况下的解,例如若=,则A,B间无相互作用时ρAB(t)=KB†0j(t)):

式中τϵ=γϵtϵ为衰减系数,Mϵ=1−e−2τϵ. 将经过分束器BS1后的光场密度算符ρ2作为初态代入(10)式即可求得经过损耗通道后的密度算符ρ3,尔后A,B两束光经过分束器BS2后再次干涉,此时光场密度算符ρout为

利用上述MZI模型(8)及(11)式,可针对任意输入光场ρin给出相应的输出光场ρout,其输入-输出关系为

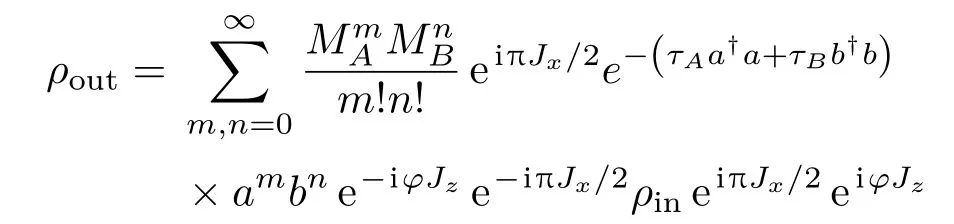
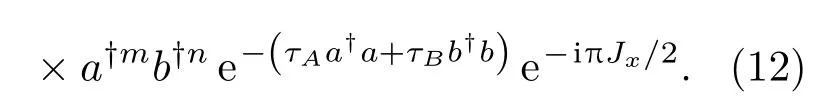
(12)式中所示的输入-输出关系是普适的,即该式可用于描述基于Fock态、Fock纠缠态、压缩态等各种光场的量子干涉雷达模型.目前仅考虑相干态的情况:若A,B两模分别为相干态|α〉与真空态|0〉时,初态光场的密度算符为

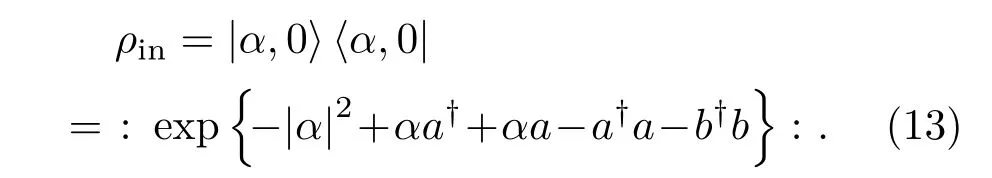
根据(13)式计算可知,ρin经过MZI后输出光场密度算符ρout为

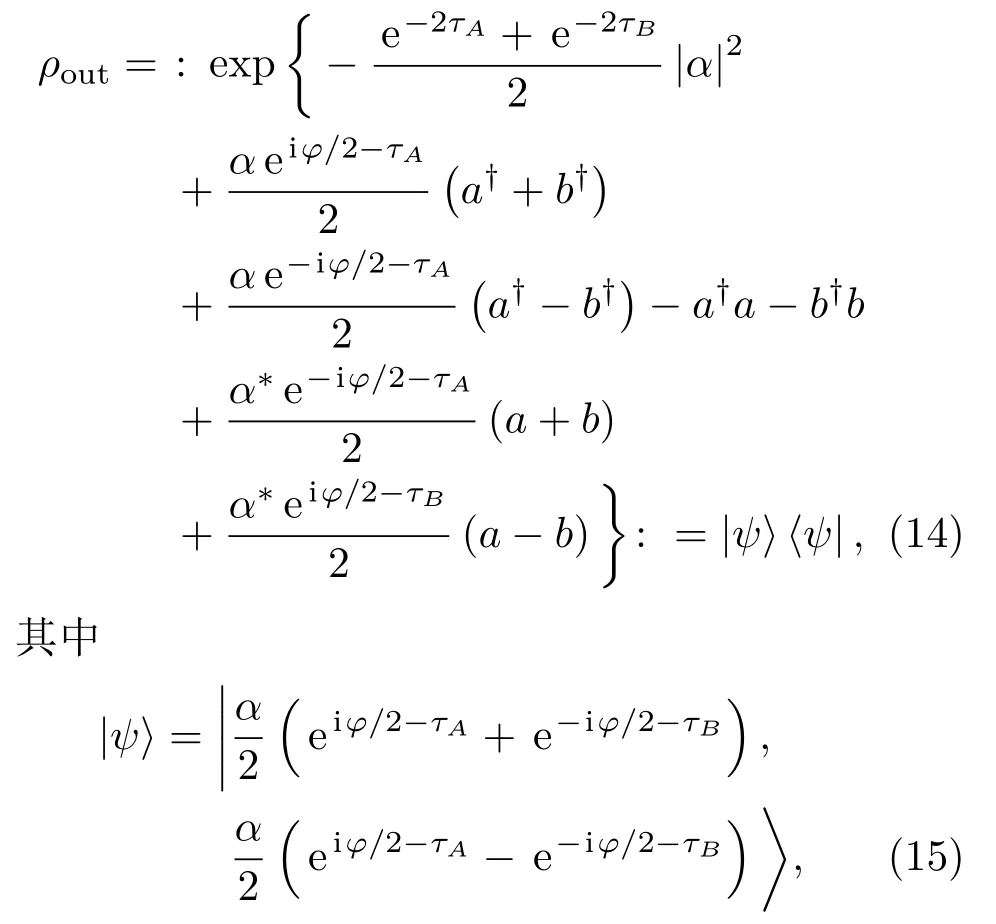
即(14)式中ρout的正规乘积形式实际上仍然代表相干态,这表明相干态光场在经过分束器、衰减通道等之后仍可保持相干态光场.

4 相位检测与估计原理

MZI的输出光场的密度算符ρout中包含与目标距离有关的相位信息φ,需进一步设计方案对ρout测量以估计相位信息φ.然而量子力学关于相位算符并没有恰当的、普适的定义,因此需引入探测算符J间接地测量相位φ.文献[26—29]中关于探测算符J引入了两种常见方案.

1)N00N方案[30]:采用如下Fock纠缠态(|N,0〉+|0,N〉)/作为探测信号,其探测算符JN00N=|N,0〉〈N,0|+|0,N〉〈0,N|,该方案能够实现O(λ/N)级别的超分辨率,且其灵敏度在无损耗情况下可达到O(1/N)的海森伯极限,但N00N这种非经典态的产生和调制非常困难(这种N00N态可通过非线性晶体的自发参量转换过程产生,量子通信中使用的纠缠态就是N=1时的N00N态,然而N较大时,自发参量转换产生的光场中N00N态的成分非常少,效率极低),且最近研究指出N00N态灵敏度受大气损耗影响极大,在损耗大于3 dB的情况下,其灵敏度随N增加而下降.

2)M&M′探测方案[31]:M&M′量子态为(|M,M′〉+|M′,M〉)/,即所有M/=M′的态及其叠加态,其相应探测算符

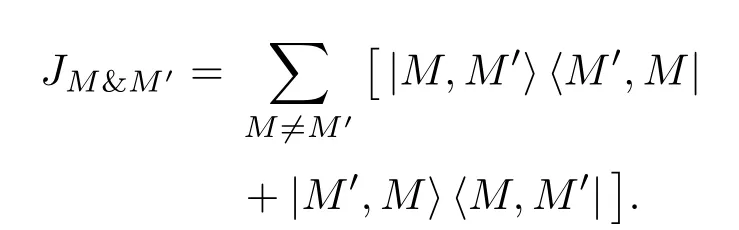
显然JM&M′的密度矩阵包含了所有相位信息的相关项,故其探测效率、信号强度高于JN00N,但M&M′光源尚未实用化且JM&M′探测方案难以设计.

由上面分析可知,由于JN00N仅能探测相干态等高斯光场中的部分Fock态成分,因此JN00N用于探测相干态或压缩态等高斯光场时其效率低、信号强度弱、信噪比低,而JM&M′的探测方案难以设计.针对这种情况,拟采用JΠ=Π的宇称算符对ρout进行测量,宇称算符Π的定义为

(16)式表明宇称算符Π在奇、偶粒子数态下的本征值分别为−1,+1,故Π又被称为奇偶算符.宇称算符Π与M&M′算符JM&M′存在如下幺正变换:

即宇称算符经分束器幺正变换后等价于JM&M′,故Π与JM&M′具有相同的探测效率.

宇称算符Π的期望值〈Π〉有许多计算方法,如文献[32]中利用算符Π作用在奇偶Fock态本征值为∓1性质,通过计算〈Π〉;文献[33]中则通过光场密度矩阵对应的Winger函数计算〈Π〉,即〈Π〉=W(0,0)π/2式中W(0,0)代表Winger函数在相空间原点处的值.以上方法前者需要求迹且涉及到无穷级数的求和,后者则需要将密度矩阵转化为Winger函数,两者的计算过程都比较复杂.

这里我们将给出宇称算符的正规乘积形式用于计算其期望值,针对宇称算符Π插入完备性公式|n〉〈n|=I,则算符Π可表示为(18)式的推导过程用到了|0〉〈0|=:e−a†a:,详情可见文献[34])

利用Π的正规乘积形式(18)及(14)式对输出端Aout光束进行测量可得

Bout端测量的结果为

其中N=|α|2代表单个脉冲的平均光子数,TA=e−τA,TB=e−τB分别代表A,B光束的大气透过率系数.这样通过对宇称算符ΠB的测量即可测得相位φ,从而精确测得目标的距离信息.

下面将讨论〈ΠB〉的实验测量方案,目前对〈ΠB〉的测量通常采用以下方法:

1)光子计数测量,在Bout端放置具有高量子效率、低噪声、低暗计数、具有单光子分辨能力的探测器,对单个脉冲内的光子进行计数并重复此计数过程即可测得〈ΠB〉,〈ΠB〉的测量值为

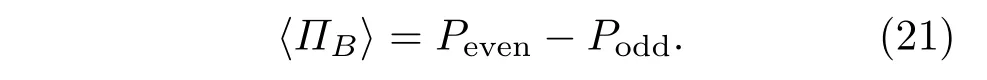
(21)式中Podd,Peven分别代表测得光子数为奇数、偶数的概率,此方案对探测器的量子效率、暗噪声、光子数分辨能力等要求较高,且需要多次测量才能得到〈ΠB〉的值,因此本方案存在着诸多的缺点;

3)平衡零拍检测,零拍检测(homodyne detection)是量子光学中常见的测量方法,文献[5]中基于平衡零拍检测设计了间接测量〈Π〉的实验方案;平衡零拍检测的原理图如图4所示.

图4 (网刊彩色)零拍检测示意图Fig.4.(color online)The diagram of homodyne detection.

式中b,l,d1,d2分别代表Bout端信号光、本振光、探测器D1和D2的湮灭算符.测量结果为

(21)式中θ为相干态|β〉的相位,YB(φ,θ)是平衡零拍探测的结果.若固定θ及相干态振幅|β|,则平衡零拍检测结果YB(φ,θ)是相位φ的函数,因此,

平衡零拍检测法能够间接测量〈ΠB〉的值,且这种方法对探测器的分辨能力、暗噪声要求较低,目前实验上多采用此方案.

5 大气衰减对干涉量子雷达性能影响

图5是经典雷达与量子雷达的脉冲信号对比图,蓝色的正弦波形代表基于振幅检测的经典雷达信号,其他颜色的脉冲波则分别代表N=4,16,64时的量子干涉雷达信号.从图5可知量子干涉雷达脉冲信号的全宽远小于经典雷达,且随着脉冲光子数N的增大而减小.

图5 (网刊彩色)经典雷达与量子雷达脉冲信号对比图Fig.5.(color online)The comparison diagram of classical radar signal and quantum radar signal.

经典雷达的回波信号呈现余弦波形,其分辨率δRC=λ/2;量子雷达的检测信号为

当大气透过率系数TA=TB=1,即无损耗时,

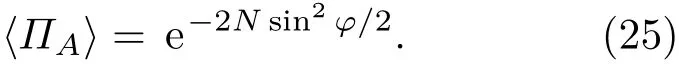
在φ≃0的脉冲峰附近有sinφ≃φ,〈Π 〉≃Ae−Nφ2/2,故其脉冲峰的宽度为δφ=1/,对应的空间分辨率为

可见与经典雷达相比,量子雷达分辨率突破了瑞利衍射极限,将分辨率提高了约倍.

存在损耗时,量子干涉雷达在φ≃0处的探测信号近似为

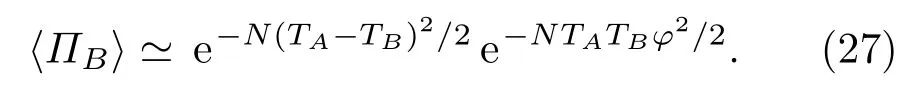
显然e−N(TA−TB)2/2项的出现使得脉冲信号的振幅变小、信噪比增加、灵敏度下降,但该项并不影响脉冲信号的宽度,分析可知此时信号的宽度为,此时空间分辨率为

综上所述,存在大气损耗的情况下,量子雷达的分辨率有一定程度的下降,但仍然保持着的关系,因此可以简单地通过提高回波的脉冲光子数来克服大气损耗造成的分辨率下降问题.

灵敏度是衡量雷达性能的另一个重要指标,量子雷达的灵敏度是相位φ的标准差,由于φ是通过〈ΠB〉间接测得的,因此,

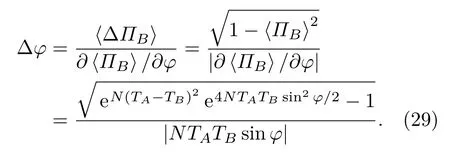
当参考光与探测光大气透过率系数相同,即TA=TB时,系统的灵敏度为

系统灵敏度Δφ在φ=0处取得最小值,此时即灵敏度达到级别的标准量子极限,但并未达到O(1/N)级别的海森伯极限,采用Fock态、纠缠态、压缩态、相干纠缠态等非经典光场的量子干涉雷达,其灵敏度均可突破标准量子极限.在实际应用中,大气损耗对量子干涉雷达灵敏度的影响也是必须考虑的内容,如Fock态N00N态、M&M′态等虽然其灵敏度可达O(1/N)级别的海森伯极限,但其灵敏度随大气损迅速下降,且损耗大于3 dB时,增大脉冲光子数N反而会导致其灵敏度的下降,从而大大限制其应用范围.

为进一步研究大气损耗对量子雷达灵敏度的影响,将不同损耗下系统灵敏度随相位φ的变化情况示于图6.

在图6中对比了脉冲光子数与大气透过率系数对量子干涉雷达灵敏度的影响.在无损耗情况下,即T=T=1时,如图6(a)所示,系统的灵敏度Δφ均在φ=0处取最小值且正比于随脉冲光子数N的增加而减小;图6(b)显示当参考光、探测光损耗相同TA=TB＜1时,系统的灵敏度Δφ仍在φ=0处取最小值,此时系统灵敏度虽然劣于无损耗情况,但灵敏度故可通过增大N克服损耗造成的灵敏度下降问题;图6(c)和图6(d)显示,当参考光、探测光损耗程度不同,即TA/=TB时,灵敏度Δφ的最小值出现在φ/=0处,且Δφ的最小值不在随N的增加而单调减小.

Distante等[35]在实验过程中证实了此现象,但其认为该现象是探测器效率以及环境噪声所致;随后Feng等[36]分析了损耗和相位起伏对量子干涉雷达灵敏度的影响,认为该现象是由相位起伏引入的噪声所致.事实上,Distante实验[35]用改装的迈克耳孙干涉仪在室内环境下进行,室内湍流极弱故由相位起伏引起的相位噪声极小几乎可忽略,故相位扩散引入的噪声并非导致该现象的真正原因;Feng等[36]在分析时仅考虑了参考光和探测光损耗相同的情况,而两者损耗不同时却可导致Δφ的最小值偏离φ=0,在实验过程中由于二者光路不同、光学器件等问题很容易导致TA/=TB的情况,这才是对Distante实验结果[35]最为合理的解释.

为进一步研究大气损耗、脉冲光子数对量子干涉雷达的影响,将灵敏度Δφ的最小值随脉冲光子数N的变化示于图7.

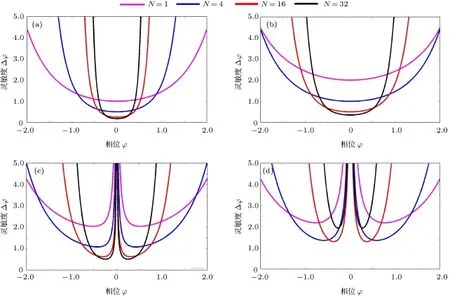
图6 (网刊彩色)不同大气衰减系数对量子干涉雷达灵敏度的影响 (a)TA=TB=1;(b)TA=TB=0.5;(c)TA=0.5,TB=0.6;(d)TA=0.5,TB=0.8Fig.6.(color online)The inf l uence of different atmospheric absorption coefficient on sensitivity of quantum interferometric radar:(a)TA=TB=1;(b)TA=TB=0.5;(c)TA=0.5,TB=0.6;(d)TA=0.5,TB=0.8.

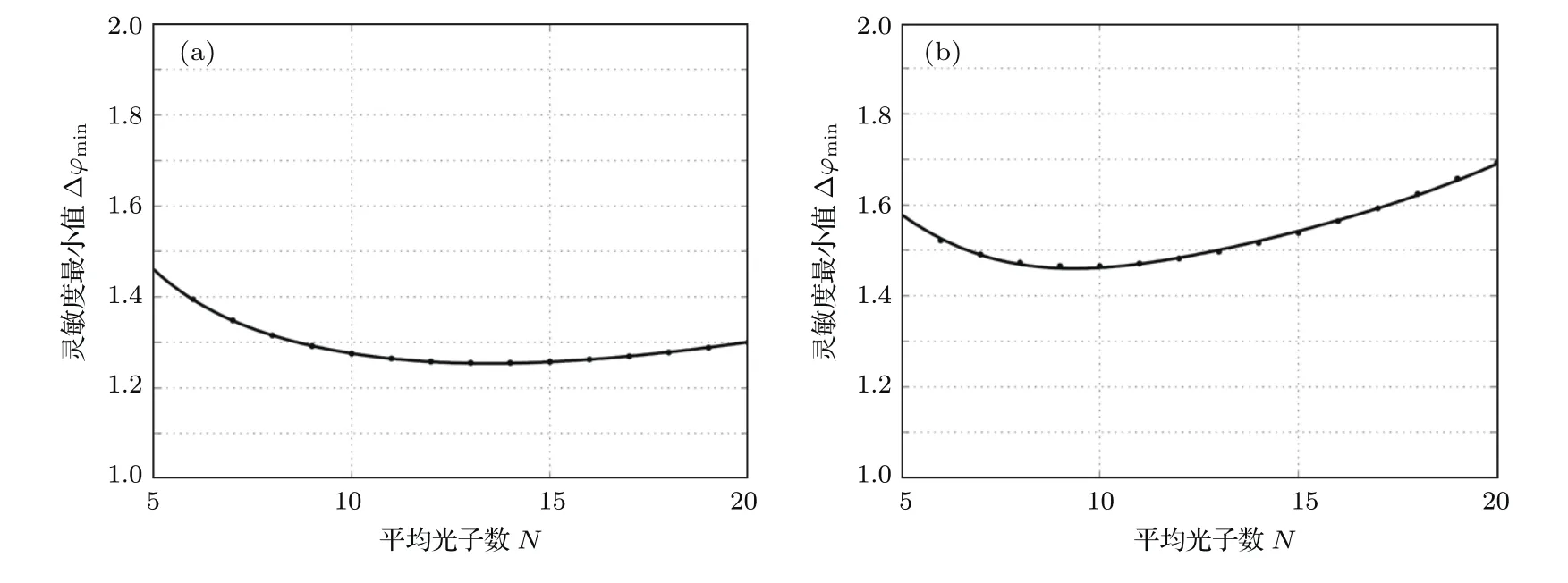
图7 平均光子数对量子干涉雷达灵敏度最小值的影响示意图 (a)TA=0.4,TB=0.65;(b)TA=0.4,TB=0.7Fig.7.The inf l uence of average photon number on the minimum of the sensitivity of quantum interferometric radar:(a)TA=0.4,TB=0.65;(b)TA=0.4,TB=0.7.

图7 显示当参考光与探测光大气透过率系数不同,即TA/=TB时,量子干涉雷达的灵敏度Δφ均随脉冲光子数N的增加而出现先减后增的情况,这种情况下单纯增加脉冲光子数N反而有可能导致系统灵敏度的下降.分析可知:图7(a)中TA=0.4,TB=0.65,灵敏度Δφ的极小值出现在Nmin≃15处,而图7(b)中TA=0.4,TB=0.7,此时灵敏度Δφ的极小值出现在Nmin≃7处,这表明当参考光与透射光损耗不同且大气透过率系数相差越大,灵敏度取极小值的脉冲光子数Nmin越小.进一步对比图7(a)和图7(b)可知:相同发射功率下,即脉冲光子数N不变时,探测光与参考光的大气透过率系数相差越小,则Δφ越小系统的灵敏度越高,反之若TA,TB相差较大则会导致Δφ的增大,致使灵敏度下降.此外,量子干涉雷达探测到的脉

冲信号〈ΠB〉=e−N(TA−TB)2/2e−2NTATBsin2φ/2,指数项e−2NTATBsin2φ/2与信号的宽度即分辨率有关,而第一项e−N(TA−TB)2/2则决定了脉冲信号的振幅,显然随着(TA−TB)2的增大,脉冲信号的振幅指数减小使得信噪比降低、灵敏度下降,与图6和图7的分析结果相符合.

综上所述,大气损耗对量子干涉雷达分辨率的影响较小,且可通过增大发射功率、提高脉冲光子数克服其不良影响;但大气损耗对量子干涉雷达的灵敏度影响较大,单纯增加发射功率、提高脉冲光子数N非但不能克服大气损耗的不良影响,甚至可能导致随着发射功率的增加使得信噪比、灵敏度进一步降低;研究显示,调节参考光的透射率使得两束光损耗相同可有效降低大气损耗引起的灵敏度下降问题.

6 总结

本文首先简要介绍了量子雷达的原理、发展历程及目前主流的三种实现方案,并对三种量子雷达方案的特点进行了比较;随后进一步对干涉式量子雷达进行了深入研究,建立了基于MZI的量子雷达模型,求解了光场在目标探测过程中的动力学演化,给出了相应的探测算符以及测量方案,分析了基于相干态光场的量子干涉雷达的灵敏度、分辨率性能;最后就大气损耗对量子干涉雷达分辨率、灵敏度等性能的影响进行深入研究.研究发现:大气损耗对分辨率的影响较小,但对灵敏度影响较大;当参考光和探测光损耗不同时,单纯增加发射功率、提高脉冲光子数N非但不能提高系统灵敏度甚至反而会导致灵敏度的下降,该发现很好地解释了Distante等[17]的实验现象.

为克服大气损耗对量子干涉雷达灵敏度的不良影响,应尽可能地调节参考光的透射率使之等于探测光的大气透过率系数.然而在真实的外场环境中,探测光不可避免地受到外界大气环境的影响,大气闪烁等大气湍流效应将导致接收到的探测光光强出现kHz级别的随机起伏,即大气透过率系数TA的随机起伏.这时应进一步详细考虑大气闪烁等对量子干涉雷达性能的影响,设计相应的方案以实现对大气透射率系数TA的实时监测,并根据对透过率TA的检测结果控制参考光的透过率,使TB=TA.然而这种监测和调节需要kHz以上的采样频率,因此其设计和实现有一定的困难,这也是我们未来进一步的研究方向之一.

[1]Xiao H T,Liu K,Fan H Q 2014J.Nat.Univ.Def.Technol.36 140(in Chinese)[肖怀铁,刘康,范红旗2014国防科技大学学报36 140]

[2]Xu S L,Hu Y H,Zhao N X,Wang Y Y,Li L,Guo L R 2015Acta Phys.Sin.64 154203(in Chinese)[徐世龙,胡以华,赵楠翔,王阳阳,李乐,郭力仁 2015物理学报 64 154203]

[3]Jiang T,Sun J 2014J.CAEIT9 10(in Chinese)[江涛,孙俊2014中国电子科学研究院学报9 10]

[4]Giovannetti V,Lloyd S,Maccone L 2004Science306 1330

[5]Gao Y,Anisimov P M,Wildfeuer C F,Luine J,Lee H,Dowling J P 2010J.Opt.Soc.Am.B27 170

[6]Lanzagorta M 2010Proc.SPIE7727 77270K

[7]Bakut P A 1967Radio.Eng.Electron.Phys.12 1

[8]Helstrom C W 1976Quantum Detection and Estimation Theory(New York:Academic Press)p95

[9]Jehle R E,Hudson D F 1992US Patent5 095 312[1992-3-10]

[10]Kumar P,Grigoryan V,Vasilyev M 2007Noise-Free Amplif i cation:Towards Quantum Laser Radar(Snowmass:14th Coherent Laser Radar Conference)p9

[11]Wasilousky P A,Smith K H,Glasser R,Burdge G L,Burberry L,Deibner B,Silver M,Peach R C,Visone C,Kumer P,Lim O,Alon G,Chen C H,Bhagwat A R,Manurkar P,Vasilyev M,Annamalai M,Stelmakh N,Dutton Z,Guha S,Chen J,Silva M,Kelly W,Shapiro J F,Nair R,Yen B J,Wong F N C 2011Proc.SPIE8163 816305

[12]Lloyd S 2008Science321 1463

[13]Tan S H,Erkmen B I,Giovannetti V,Guha S,Lloyd S,Maccone L,Pirnadola S,Shapiro J H 2008Phys.Rev.Lett.101 253601

[14]Guha S,Erkmen B I 2009Phys.Rev.A80 052310

[15]Lopaeva E D,Berchera I R,Degiovanni I P,Olivares S,Brida G,Genovese M 2013Phys.Rev.Lett.110 153603

[16]Dutton Z,Shapiro J H,Guha S 2010J.Opt.Soc.Am.B27 A63

[17]Nair R,Yen B J,Shapiro J H,Chen J,Dutton Z,Guha S,Silva M P 2011Proc.SPIE8163 816310

[18]Ekert A K,Rarity J G,Tapster P R,Palam G M 1992Phys.Rev.Lett.69 1293

[19]Allen E H,Karageorgis M 2008US Patent7375802 B2

[20]Smith J F 2010Proc.SPIE7702 p131

[21]Yurke B,McCall S L,Klauder J R 1986Phys.Rev.A33 4033

[22]Breuer H P,Francesco P 2002The Theory of Open Quantum Systems(Oxford:Oxford University Press)pp161,162

[23]Ren Y C,Fan H Y 2016Acta Phys.Sin.65 030301(in Chinese)[任益充,范洪义 2016物理学报 65 030301]

[24]Howard C 1999Statistical Methods in Quantum Optics 1:Master Equation and F-P Equation(Berlin Heidelberg:Springer-Verlag Press)p9

[25]Fan H Y,Hu L Y 2010The Thermal Entanglement Entangled-State Representation of Open Quantum System(Shanghai:Shanghai Jiao Tong University Press)p91(in Chinese)[范洪义,胡利云2010开放量子系统退相干的纠缠态表象论(上海:上海交通大学出版社)第91页]

[26]Kok P,Braunstein S L,Dowling J P 2004J.Opt.B6 S811

[27]Kok P,Boto A N,Abarms D S,Williams C P,Braunstein S L,Dowling J P 2001Phys.Rev.A63 063407

[28]Knysh S,Smelyanskil V N,Durkin G A 2011Phys.Rev.A83 021804

[29]Lee T W,Huver S D,Lee H,Kaplan L,McCracken S B,Min C,Uskov D B,Wildfeuer C F,Veronis G,Dowling J P 2009Phys.Rev.A80 063803

[30]Resch K J,Pregnell K L,Prevedel R,Gilchrist A,Pryde G J,O’Brien J L,White A G 2007Phys.Rev.Lett.98 223601

[31]Huver S D,Wildfeuer C F,Dowling J P 2008Phys.Rev.A78 063828

[32]Wang Q,Hao L L,Zhang Y,Xu L,Yang C H,Yang X,Zhao Y 2016Opt.Express24 5045

[33]Jiang K,Lee H,Gerry C C,Dowling J P 2013J.Appl.Phys.114 193102

[34]Fan H Y 1992Representation and Transformation Theory in Quantum Mechanics(Shanghai:Shanghai Scientif i c and Technical Publishers)p44(in Chinese)[范洪义1992量子力学表象与变换论(上海:上海科学技术出版社)第44页]

[35]Distante E,Jezek M,Andersen U L 2013Phys.Rev.Lett.111 033603

[36]Feng X M,Jin G Y,Yang W 2014Phys.Rev.A90 013807