多量子比特核磁共振体系的实验操控技术∗

潘健1) 余琦1) 彭新华1)2)

1)(中国科学技术大学,中国科学院微观磁共振重点实验室和近代物理系,合肥 230026)

2)(中国科学技术大学,量子信息与量子科技前沿协同创新中心,合肥 230026)

1 引 言

20世纪90年代以来,量子信息与量子计算科学发展迅速[1,2].人们意识到量子计算机在处理某些特定问题时优越于经典的计算机.从早期的Deutsch-Jozsa算法[3]、Shor质数分解算法[4]、Grover搜索算法[5]等开始,一系列不同的量子算法如量子线性方程组算法[6]、高斯和算法[7]等被陆续提出.与此同时,量子信息处理器还被广泛地用于量子模拟[8]、量子信息纠错[9]、量子度量[10]等方面的研究.针对不同的量子体系,开发出了一系列实验技术以满足不同的实验需求.随着研究的不断深入,从实验上实现理论方案所需要的量子比特位数也在不断增加.为了能够最终真正地将量子计算的巨大潜能得以实现,必须不断地提高实验体系可操控的量子比特位数,掌握多比特量子操控技术.然而,到目前为止还只有少数的物理体系(如离子阱[11]、超导回路[12]、核磁共振(nuclear magnetic resonance,NMR)[13,14]等)能实现复杂的多比特(≥7个量子比特位)的实验方案.

NMR平台是一个很好的量子方案测试平台,该平台60多年的控制技术的发展提供了丰富而又精准的量子操控手段.很多量子算法都是在NMR平台上得到了最早的实验验证[15,16].近几年来,一些多量子比特实验方案也在NMR平台上得以实现.在2000年和2001年,Knill等[13]和Vandersypen等[14]分别利用巴豆酸(crotonic acid)和全氟丁二烯基铁络合物(perf l uorobutadienyl iron complex)这两种不同的7比特样品实现了7比特赝纯态的制备和Shor算法的演示,以此揭开了多比特NMR实验的序幕.后续的很多7比特实验方案都利用了巴豆酸样品[17,18].2006年,Negrevergne等[19]实现了12比特的赝纯态制备.在拓展系统量子比特位数方面,选择和制备合适的样品一直是一个非常大的挑战.最近我们提出了最优控制的量子经典杂化的反馈控制方案[20],并在实验中实现了7量子相干的量子控制.这个方法克服了完全经典最优控制中对计算资源要求最苛刻的部分,对多量子比特系统提供了一个有效的控制手段.随后,这个方法被应用到了一个新的12比特样品上[21].

本文介绍NMR平台下的多量子比特体系的实验操控技术.首先阐述操控多量子比特NMR体系实验中的基本困难及其原因,然后介绍我们在7量子比特赝纯态制备以及其他多量子比特实验中用到的一系列实验技术,最后给出展望.

2 多量子比特NMR实验中的技术困难

目前2到4位的少量子比特NMR实验已经形成为较完善成熟的实验技术,然而在多比特NMR实验中还有很多的技术困难需要解决.为了克服这些实验困难,已发展出了很多实验技术方法.

首先是谱线信噪比以及分辨率的问题.随着自旋数目的增加,谱线强度大致以指数形式减弱,从而导致谱线信噪比迅速降低.同时由于不少核与核之间的J耦合系数很小,导致相关峰劈裂出来的频率间隔很小,会堆叠在一起无法精确区分彼此的位置.在实验中多个峰彼此叠加在一起形成非常复杂形状的谱线,导致无法直接获取精确的实验信息.这一关键性问题涉及到NMR体系的可扩展性[22].

其次是对多量子比特实现有效的脉冲操控以及进行有效的数值模拟问题.对于n量子比特的样品,描述整个量子体系运动的薛定谔方程需要构建2n维度的密度矩阵,从而模拟体系状态的运算量将以指数速度攀升,这极大地限制了优化算法(如GRAPE算法[23])的搜索效率.

第三是如何进行有效的初态制备问题.已经提出了多种方法来进行赝纯态制备[24−26],然而主要问题是要么实验的次数随比特数指数增加,要么得到的赝纯态信号强度随比特数指数减小.例如Vandersypen等[14]在他们7比特实验中利用时间平均法叠加了36次实验才制备出了赝纯态.Knill等[13]发明了猫态制备法有着简洁而有效扩展的形式,理论上对n比特样品最少只需要n次实验的叠加,然而信号强度随比特数指数减小.不管怎样,猫态制备法依然能在10量子比特左右的NMR体系上有很好的应用[19].

第四是线路优化问题.对于多量子比特实验,往往需要复杂的操作来实现所需的实验线路.除了实验线路中所必须的基本操作外,往往还要添加很多去耦脉冲来消除不需要的系统哈密顿量演化.随着操作脉冲的增加,整个线路的累积误差也会越来越大,如果不进行有效的线路优化,实验结果往往与理论预期偏差很大.

最后是对实验结果快速有效读出的问题.对多量子比特NMR体系的量子态进行完全重构所需的读出脉冲个数随量子比特位数也是以指数速度增加的.为了简化实验的复杂度,有时只进行部分子空间态层析.也有一些新型的态层析方法被提出,用来提高结果读出的效率[27,28].

3 NMR量子寄存器

下面我们以巴豆酸(crotonic)样品为例,结合7比特赝纯态制备以及相关实验来对其中的一些多比特实验技术进行介绍.巴豆酸分子的结构及在303.0 K温度下Bruker AV-400 MHz的NMR谱仪上测得的样品参数如图1(a)所示,样品溶剂为重水.7个量子比特由C1,C2,C3,C4,M,H1和H2自旋组成,按照这个顺序分别标记为第1—7量子比特,其中M是三个完全等价的氢核组成的甲基氢(后面我们将介绍怎样将甲基中的三个氢自旋作为一个量子比特使用).

图1 (网刊彩色)7比特量子寄存器 (a)巴豆酸分子的化学参数,对角元表示化学位移,非对角元表示J耦合常数,单位为Hz;(b)13C(蓝色)和1H(红色)的热平衡谱Fig.1.(coloronline)7-qubitquantum register:(a)Chemical parameters of crotonic acid molecule;the diagonal elements denote the chemical shifts and the non-diagonal elements denote the J-coupling constants;the unit is Hz;(b)13C(blue)and1H(red)thermal equilibrium spectra.

其中,νi代表第i个核的化学位移,Jjk代表j核和k核自旋之间的标量J耦合大小,σiz代表第i个核自旋泡利算符.实验中测得的参数见图1(a),自旋13C和1H的热平衡谱见图1(b).

4 多比特NMR实验中的操控技术

4.1 射频选择方法

静磁场和射频场的不均匀性会造成脉冲的不完美性,通过对水峰信号进行章动实验能够测试射频场的不均匀性,如图2(b)中蓝线所示,随着施加的脉冲时间的增加信号强度会振荡减小.通过射频选择方法[29]可以减小这种不完美性的影响.此方法利用核章动速率和脉冲功率之间的关系来选择性地挑选出一小部分空间的样品.在此小空间内,样品感受到的射频脉冲功率近乎相等,同时由于选择性地挑选出了部分空间的样品,有效样品的空间区域大大减小,从而此部分感受的静磁场不均匀性比整个样品空间的磁场不均匀性小很多,从而提高了谱线分辨率.

射频选择方法是受DANTE序列的启发[30].我们采用文献[29]中的射频选择序列：

其中Rx,±y(θ)分别代表沿着x,±y轴旋转θ角度.上面序列中旋转角度针对的是线圈中心位置附近的样品,角度α满足mα=π/2,整个序列中的脉冲都是硬脉冲激发.对于线圈中心附近的样品,上述序列净作用相当于绕x轴旋转π/2.如果开始态沿z方向,在m次循环后对应于线圈中心附近样品的态将被激发到y方向,最后的Ry(2mπ)脉冲将作为自旋锁定的脉冲,不改变y方向的态.而对于不在线圈中心附近的样品,由于射频不均匀性导致激发幅度的减小,翻转的角度不再是2π(而是β＜2π)或者α,因此在m次循环后态将被激发到x-z平面,最后的Ry(2mπ)脉冲等效于一个回聚的形式(旋转回波)将最终态转向z方向.因此序列(2)能够选择性地挑选出线圈中心附近一小部分空间的样品,从而在抑制射频脉冲的空间不均匀性的同时也能进一步提高谱线的分辨率.实验中我们测试了这个序列的效果,如图2(a)所示.当取m=80时,能将水峰的半高宽从1.95 Hz降到1.02 Hz,伴随的代价是信号强度衰减到原有的8.0%.施加序列(2)后,对水峰信号进一步进行章动实验的结果(图2(b)中的红线)可以看出,随着施加的脉冲时间增加,信号强度改变很小,射频场的不均匀性得到了有效的抑制.

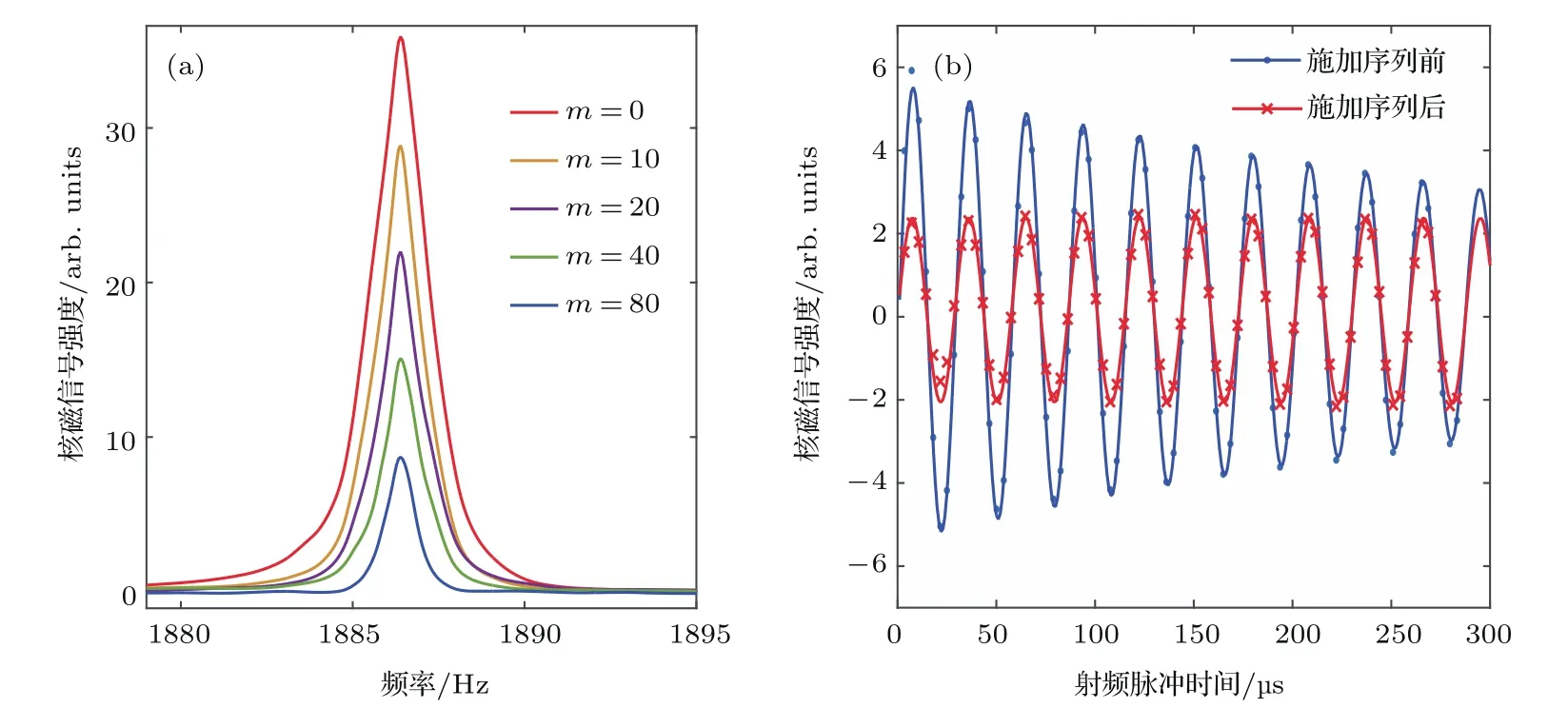
图2 (网刊彩色)射频选择方法的实验测试结果 (a)施加序列(2)前后水的热平衡谱,图中不同谱线对应序列(2)中的m分别取0,10,20,40,80的效果;(b)章动实验测试结果,图中蓝线和红线分别代表施加射频选择序列前后水的射频章动实验结果,红线信号放大了5倍,其中红线施加的射频选择序列中m=80Fig.2.(color online)Experimental results for radio-frequency(RF)selection method.(a)Thermal equilibrium spectra of water with/without the sequence(2).Different spectra correspond to m=0,10,20,40,80 in the sequence(2),respectively.(b)RF nutation experiments;the blue and red curves represent the nutation signals of water without and with the sequence(2);the signal of the red curve is amplif i ed by 5 times with m=80.

4.2 甲基氢自旋1/2子空间选取

甲基具有三个完全等价的氢自旋,无法对这三个氢自旋分别进行操作,因此不能作为三个量子比特使用.但是通过选取甲基上氢自旋态的子空间,能将它们作为一个有效自旋1/2的粒子(即一个量子比特)利用.这是利用了甲基上三个等价氢自旋的对称性,它们的态空间能由一个自旋3/2的子空间和两个自旋1/2的子空间组成.最初的热平衡态包含这两种自旋类型的极化,利用图3的操作序列能消除自旋3/2子空间的极化,而只保留自旋1/2子空间的极化,相当于在自旋1/2子空间做投影操作.因此,经过这一步之后,我们就能将整个巴豆酸分子体系作为一个7量子比特的样品进行操作.

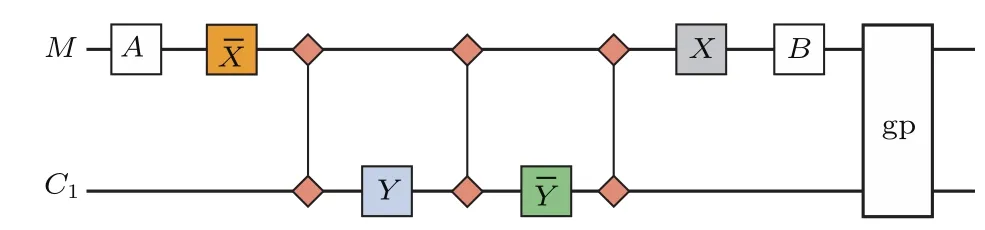
图3 (网刊彩色)甲基上三个等价氢自旋态的自旋1/2子空间选取的操作序列,图中Y和的方框分别代表绕y轴和−y轴π/2的旋转,X和的方框分别代表绕x轴和−x轴π/2的旋转;A,B分别代表绕x-y平面内与x轴夹角为68.2°和116.6°的轴π/2的旋转;两个比特间的连接线代表演化时间为1/4J的J耦合演化,这里J是甲基上碳和氢自旋之间的耦合常数,gp表示z方向的梯度脉冲Fig.3.(color online)Sequence of the selection of spin-1/2 components of the methyl protons.Here Y and represent π/2 rotation along the y and −y axis,respectively.X and represent π/2 rotation along the x and −x axis,respectively.A,B represent π/2 rotations along the axis in the x-y plane with the phases of 68.2° and 116.6°,respectively.The connecting line between the two qubits represents the J coupling evolution with the duration of 1/4J.Here J is the J-coupling constant between spins13C and1H in the methyl group.gp denotes pulsed fi eld gradient along z direction.

4.3 形状脉冲与组合脉冲

按照量子控制的理论,单比特旋转操作和两比特CNOT门能构成普适的量子逻辑门组,可以实现任意的幺正操作[1].在NMR体系中CNOT门可以拆分成[31]

这里在量子比特i上的单量子比特旋转Riα(θ)表示绕α(=x,y,z)轴做θ角度的旋转,J耦合演化UJ(1/2J)=e−iσ1zσ2zπ/4. 因此,单比特旋转操作和J耦合演化能实现任意的幺正操作.

当同核自旋之间的化学位移频率相差比较大时,可通过选择性的形状脉冲来实现单比特的旋转.一般而言,形状脉冲的时间长度和核与核自旋之间的化学位移之差成反比.常用的的形状脉冲是Gaussian型的软脉冲[32].当同核自旋之间化学位移相差在104Hz左右时(常见于13C谱),1 ms左右时间长度的Gaussian软脉冲能很好地实现单核π/2,π旋转操作.当化学位移相差只有1 kHz左右(常见于1H谱)时,实验效果表明对于π旋转操作用Hermite型[33]的软脉冲会有更好的实验效果.

除了单比特操作外,实验中还经常用到硬脉冲操作来实现所有13C核或者1H核的同时旋转.一般整个通道的谱宽往往很大(104Hz量级),由于偏共振效应,处于谱两边位置的核实际旋转角度会比谱中心位置的核的旋转角度要小.施加脉冲过程中核之间的J耦合也会造成一些误差.因此,我们采用组合脉冲[34]来实现对所有1H核的π旋转,以消除硬脉冲的偏共振效应、系统内部哈密顿量等因素所造成的脉冲不完美性的影响.

4.4 脉冲编译技术

在利用软脉冲实现单比特旋转操作时,由于偏共振效应和系统的J耦合演化,脉冲的效果并不完美.为了弥补每个软脉冲带来的局部误差,Laf l amme等[35]开发了脉冲编译程序,可计算出软脉冲的误差.引入一系列的化学位移与σzσz耦合项的前置和后置误差项,分别用来代表偏共振效应与核耦合效应引起的误差,表达式如下：

式中Hrf代表射频场的哈密顿量,代表化学位移演化的前置与后置误差项,代表σzσz耦合项相应误差项.我们需要优化这四项参数,使保真度[36]

最大.这项工作可以通过Matlab数值优化程序得以实现,也可以通过平均哈密顿量理论计算出低阶的近似[37].

结合巴豆酸样品,以C1核π/2旋转为例,我们给出一个具体的Matlab数值优化结果,如表1所列.对角项参数是化学位移演化的弥补误差和.除了C1核外,其余核均有而=138.35°. 对角线上方的非对角元给出了两核J耦合演化的前置误差弥补,对角线下方的非对角元给出了后置误差弥补.经过优化误差项后,该脉冲的保真度为ΦS=0.9999.

表1 C1核π/2 Gaussian脉冲的前置误差项与后置误差项,数值以角度制形式给出Table 1.Pre-errors and post-errors of π/2 rotation pulse on C1with Gaussian shaped.The unit of the values is degree.

表2列出了利用形状脉冲对7个量子比特实现单比特的π/2和π旋转的基本脉冲参数以及经过脉冲编译后的保真度.

4.5 脉冲序列编译

对于一定的量子信息处理任务,需要施加一系列的脉冲并演化组合成一定的脉冲序列来实现.在最终设计实际用到的实验脉冲序列时,我们需要考虑如下几个因素：

1)尽量消除脉冲的累积误差,使得整个序列具有较高的保真度,例如前面提到的每个软脉冲有前置误差和后置误差,通过调节脉冲序列的参数尽量让它们能够彼此抵消掉;

表2 400 M谱仪上单量子比特旋转脉冲参数设置Table 2.Parameters of pulses for single-qubit rotations in 400 M spectrometer.

2)在演化期间添加去耦π脉冲,在实现某两个核之间的J耦合时,我们需要对其余核施加去耦π脉冲,随着比特位数的增加,去耦脉冲个数会迅速增加,使得序列变得非常复杂;

3)尽可能地减少脉冲操作数目,将某些操作进行合并或者简化,一般情况下,所用到的脉冲越少最后的实验误差也会越小.

针对上述问题,La fl amme等[35]开发了一套脉冲序列的编译程序.该程序能够自行优化每个脉冲的入射角度、脉冲之间的时间间隔、去耦π脉冲的位置,并能够对某些特定的脉冲进行合并.程序用到的原理如下：

1)将绕z轴旋转操作用通过改变脉冲相位或接收相位来等价实现;

2)利用旋转坐标系,对每个核进行相位追踪,结合1来补偿掉所有化学位移误差,例如为了消除单个脉冲后置化学位移误差,可以在此脉冲后加一个z轴旋转来抵消,此操作可以归并到改变核的观测相位即可,同时在旋转坐标系中能大大简化去耦π脉冲的个数,因为不需要考虑再去消除化学位移演化;

3)利用态假设来吸收一部分误差或者去除一些脉冲操作,例如序列中间某个时刻某两个核处于最大混态,导致两者之间的J耦合是没有作用的,也不需要添加去耦操作;

4)尽量将一些π/2,π脉冲(含去耦脉冲)彼此合并消除;

5)数值优化脉冲之间的时间间隔,主要是为了补偿或者消除J耦合的误差,并使得整个序列最终残余误差最小.

4.6 子空间GRAPE

利用GRAPE(gradient ascent pulse engineering)[23]算法可以有效地搜索出实现目标操作的脉冲.其巨大的优势在于将体系的内部哈密顿量以及一些脉冲的不完美性(如静磁场和射频场的不均匀性)考虑在内,通过数值的优化获得保真度较高的形状脉冲以实现想要的操作,从而避免了对实验线路繁琐的拆门搭建过程,并能大大减少整个实验线路所需要的时间,减小退相干效应对实验结果的影响.此项技术在3—5比特NMR实验中已经得到广

如果目标操作U可以拆解成直积的形式U=UA⊗UB,其中UA,UB分别只作用在A,B这两个子空间内,那么只要搜索得到的脉冲满足在A子空间A的作用下趋于UA,且在B子空间B的作用下趋于UB,在总的系统哈密顿量的作用下所得的脉冲作用效果就近似趋向于U.因而把在7量子比特空间搜索U脉冲的问题转换成在4量子比特子空间A和3量子比特子空间B里寻找一个脉冲,使得其在两个子空间内的作用分别同时趋于UA,UB.这样就能把一个7比特GRAPE问题分解成2个4比特和2个3比特GRAPE问题(因为这种拆分哈密顿量时有2个A和2个B),从而使得问题得到降维,大大加快程序的运行速度.

按照不同的目标操作,我们可以将样品按照不同的方式划分子空间.例如,除了按照样品空间结构来划分子空间外,还可以将巴豆酸分子分成由4个13C和3个1H组成的两个子空间.这种划分法非常适合于搜索单通道GRAPE脉冲情形.子空间GRAPE对单比特脉冲非常有效,对于巴豆酸样品,很容易在1 h内就算出整体保证度在99.5%以上的单比特旋转操作,然而对于多比特操作(2个或者2个比特以上的操作),用子空间GRAPE方法算出来的脉冲整体保真度往往非常低,经验表明即使子空间脉冲保真度都到达99%以上,整体保真度也只有不到10%的概率会在90%以上.因此在计算多比特GRAPE脉冲时需要反复调试.表2中的H1与H2核的π脉冲就是用子空间方法计算出来的.

4.7 态读出:量子态层析技术

提取量子计算的结果,必须对末态进行测量.实际上,NMR系综量子计算的读出是一个系综平均弱测量过程.通过采集在接收线圈中由于自旋磁泛的应用.

然而随着量子比特数的增加,体系的希尔伯特空间维度将呈指数增加,计算GRAPE脉冲所需要的时间以及难度也会呈指数增加.对于7比特样品GRAPE算法一般只能计算出简单的单量子比特操作,对多比特操作一般较难算出高保真度的脉冲.即使对于单比特操作,也往往需要较长的时间(大约半天)才能得到99%以上高保真度的脉冲.为了克服GRAPE算法的这个缺点,我们可以利用子空间GRAPE方法[35]进行搜索,即将整个样品希尔伯特空间分割成几个小的子空间的组合,分别在子空间中进行数值优化,从而降低目标操作的维度,大大提高GRAPE程序的效率.下面以巴豆酸样品为例解释子空间GRAPE方法的原理.

从样品的结构和参数(图1(a))上可以看出,可以把整个7量子比特分成两部分:A={C1,C2,M,H1}和B={C3,C4,H2}.A和B子系统之间只有C2与C3之间有较强的J耦合.因此,(1)式中的整个7比特哈密顿量ˆH可以近似等效看成A,B两部分子空间哈密顿量:矩进动感应的振荡电压,一个时间响应的自由感应衰减(free induction decay,FID)信号被NMR谱仪的探头接收,经过傅里叶变换,将原来复杂的FID信号转化为频域的频谱图,核自旋态信息就被包含在这些傅里叶谱图里,可以通过谱线积分来获得每个峰的幅度、相位等信息.

然而随着比特数的增加,用直接的谱线积分方法来获得精确的谱线信息变得越来越困难.因此我们可以利用最小二乘法对谱线进行拟合,从而获得每个峰的位置、幅度、相位、半高宽这些有用信息,以便进行进一步的实验数据处理.在液态NMR体系中,共振峰的形状近似是洛伦茨型[38]的,傅里叶变换的谱线信号S(ω)可由下式描述：

Re代表取实部,Ak,φk,λk,ωk分别代表第k个共振峰的幅度、相位、半高宽以及中心频率.通过Matlab可以拟合出这些参数,从而得到所有有用的信息.在实际拟合过程中,借助于热平衡谱能设置较好的参数初始值,这样能大大提高拟合的速度并最终得到拟合结果.

如果想要知道量子态全部的信息,通常采用的方法是量子态层析技术[39],运用不同的观测脉冲将描述系统输出态的密度矩阵完全重构出来.对于n量子比特样品,其密度矩阵的维度是N=2n,由N2−1个独立的参数决定.对任意的量子态进行完全重构可以用5N−6个观测量来实现[27].随着量子比特数n的增加,进行完全量子态重构所需要的测量次数是指数增长的.对于多量子比特量系统,实验上已经非常难以实现完全的态层析.针对不同的计算目的,如果我们只关心密度矩阵的部分子空间信息,可以只对系统小的子空间进行读出,以大大减少读出脉冲的个数[40].近年来一些量子态重构的方案不断被提出来用以减少态重构过程的测量次数.例如基于在子空间上进行的幺正操作来进行态重构[27],这种方法可对多种类型的量子态进行重构,尤其是针对可以很好地近似为矩阵乘积的量子态.还可以通过压缩感知的方法对接近纯态的密度矩阵进行自适应测量,将测量次数降低到2N−1次[28],但随量子比特数的增加依然需要指数增长的资源.

4.8 赝纯态制备

量子算法一般要求将所有的计算量子比特制备到一个合适的初态,通常为基态|0⊗n〉.然而,室温下NMR自旋体系处于热平衡态是一个高度混和态,不适合作为量子计算的初态.Vandersypen和Chuang[41]以及Cory等[42]提出了赝纯态的概念来代替纯的基态,使得液态分子NMR量子计算成为可能.赝纯态的密度矩阵具有如下形式:

式中n代表比特数,I是2×2的单位矩阵,ε∼10−5代表ρpps的有效纯度.除了信号强度减小ε外,(6)式中的赝纯态和纯态|0⊗n〉有相同的演化规律和观测信号.

然而制备如此一个赝纯态并非一件容易的事,因为赝纯态需要引入非幺正的过程.至今已经发展了许多制备方法,例如空间平均法[24]、时间平均法[25]、线选脉冲[26]等.2000年,Knill等[13]提出了猫态法制备赝纯态的方案,此方法具有简洁而有效扩展的形式,很容易应推广到多量子比特体系实验中.下面我们以巴豆酸样品为例,结合以上的各种技术,通过猫态法实验制备7比特赝纯态.

4.8.1 猫态制备法

猫态制备法由编码和解码两部分组成.编码过程是将态由IIIIσzII制备成最大量子相干态σxσxσxσxσxσxσx, 通过相位循环制备最高7阶的量子相干项I+⊗7+I−⊗7,这也对应于猫态中的相干项,这里I±=(σx±iσy)/2,σx,y,z为泡利算符.图4(a)是在巴豆酸样品中实现这个编码过程的量子线路图.原则上,通过7次的相位循环实验,其中第k次对每个比特施加绕z轴旋转ϕk=2kπ/7角度(即在第k次相位循环脉冲相位增加ϕk),将7次实验累加起来,就能得到只含有7阶量子相干项态.为了进一步消除0量子相干项,我们采用14次相位循环,其中第k次对每个比特施加绕z轴旋转ϕk=角度.

解码过程是将最高7阶量子相干项态I+⊗7+I−⊗7解码为辅助比特标记的赝纯态00000σz0,这里态|0〉〈0|简记为0.这样就得到了以H1作为标记位的6比特赝纯态.图4(b)是在巴豆酸样品中实现这个解码过程的量子线路图.对这个线路做一定的修改,可获得以7个核中的任意一个核自旋作为标记比特的赝纯态,本质上没有任何区别.

图4 (网刊彩色)利用猫态法在巴豆酸样品上制备标记赝纯态的量子线路图 (a)编码过程;(b)解码过程Fig.4.(color online)Quantum circuit for pseudo-pure state preparation using cat-state method on the crotonic acid:(a)Encoding procedure;(b)decoding procedure.

4.8.2 实验过程与结果

7比特标记赝纯态制备实验在Bruker AV-400 MHz谱仪上进行.实验的基本过程为:1)对样品施加4.1节中的射频选择脉冲;2)通过π脉冲和梯度场消除除甲基氢外的其余所有核自旋的极化,然后通过4.2节中甲基氢自旋1/2子空间选取序列制备态IIIIσzII;3)通过猫态法制备赝纯态的编码和解码过程获得标记的赝纯态00000σz0;4)通过测量确认态的信息.

首先通过4.4节中的脉冲编译技术计算并优化每个核自旋π/2和π脉冲的前置和后置误差(参见表1和表2),用到了Gaussian型和Hermite型软脉冲,利用4.6节中的子空间GRAPE程序计算H1和H2上的GRAPE脉冲.然后通过4.5节中的脉冲序列编译技术对甲基氢自旋1/2子空间选取(图3),并对猫态法制备赝纯态的编码和解码(图4)的量子线路进行优化,自行进行添加去耦脉冲、消除误差、合并脉冲等操作,经过编译后整个实验序列时间只需要132 ms,脉冲序列的理论末态保真度为97.48%.实验中我们在样品中施加优化通过相位循环后优化的脉冲序列,最后通过谱线测量对实验结果进行检测.

由于标记赝纯态具有00000σz0的形式,因此赝纯态的特征是,在H1上的观测(对H1施加π/2旋转的读出脉冲)只有一个对应于其他6个核自旋在|000000〉〈000000|态的单峰出现,如图5(a)所示,在其他峰的位置没有可观测的信号,与实施图4之前的参考信号的强度之比大约为14%.为了进一步确认实验结果,我们分别对其他6个核自旋也进行了读出操作,即对每个核自旋施加π/2旋转的读出脉冲,观测对应核自旋的谱线信息,理论上应为2条方向相反、幅度相等的双峰出现,如图5(b)—(h).图5所示的实验谱与理论预期基本相符.

图5 (网刊彩色)标记赝纯态00000σz0制备的实验结果 (a),(b)和(c)分别代表H1,H2和M核的实验谱;(d),(e),(f)和(g)分别代表C1,C2,C3和C4核的实验谱;图中蓝线代表标记赝纯态的实验谱线,红色代表热平衡态谱线,所有谱线都是通过对该核自旋施加π/2旋转的读出脉冲获得Fig.5. (color online)Experimental reulsts of preparing 7-bit labeled pseudo-pure state 00000σz0:(a),(b),(c)represent the experimental spectra of H1,H2and M respectively;(d),(e),(f)and(g)represent the experimental spectra of C1,C2,C3and C4respectively.The blue lines are for labeled pseudo-pure state and the red ones are for thermal equilibrium state.The M signal is amplif i ed by 4 times.All spectra are recorded after a π/2 reading-out pulse on the corresponding spin.

实验误差主要有五方面:1)对于经过脉冲优化后的序列,序列整体操作的理论误差仍有2%左右;2)样品参数测量不是完全精确的,会进一步影响脉冲序列的保真度;3)尽管实验中通过射频选择方法消除了大部分脉冲和磁场不均匀性的影响,但是实际实验中仍然存在脉冲的不完美性;4)弛豫的影响;5)实验谱线分辨率不够和信噪比低对实验读出结果的影响等.

5 展 望

本文结合7比特赝纯态制备以及其他有关实验介绍多比特NMR实验技术,尚有很多其他方面的多比特实验理论和技术未能述及.就像之前的低比特实验技术一样,相信在NMR中发展的多比特量子控制技术在不久的将来也会不断应用到诸如NV色心、离子阱等量子体系中,使这些技术得到更广泛的应用.

虽然近几年量子计算和量子信息方面取得了不少突破,然而多量子比特实验还有更多的问题有待解决.这里,我们简要地总结了NMR多量子比特实验未来可能研究的重要问题.

1)开发新型的多量子比特样品.目前已经开发成熟的多比特样品还很少,具有优异的系统参数的样品能够很大程度上简化实验的难度.例如我们希望能尽可能地区分开谱图上每个核的峰,核与核之间耦合系数不要太小,退相干时间能尽可能地长等.最近有些实验方案开始利用液晶样品,这是源于液晶样品有较强的偶极-偶极耦合,可能有助于提高GRAPE算法的成功率[43].

2)提高信噪比.目前已有的NMR谱仪静磁场强度已达到20多特斯拉,通过增加静磁场强度在未来已经很难再有效地提高多比特实验中的信噪比.很多理论方案都在试图克服核磁体系的可扩展性问题.其中冷却算法[44]能有效地提高系统初始极化度,是一个很有可能解决这个难题的方法.近期也有不少新型冷却算法研制出来.

3)实现更复杂的量子操控.如何在多量子比特平台上实现复杂的量子操控还是一个未解决的问题.基于GRAPE技术,很多新的优化算法试用于多量子比特体系上.最近也有人试图通过闭环控制来实现量子反馈[20],以此来克服在经典计算机实现GRAPE算法所需指数增长的时间问题.

4)快速有效的系统模拟、态读出等其他有效性问题.这些问题都源自于描述量子系统的希尔伯特空间维度随着量子比特位数以指数速度的增长,传统的计算方法所耗费的资源太大,需要我们从理论上设计研制出新的方案来解决这个问题.

感谢加拿大R.Laf l amme实验组提供的脉冲和序列编译程序;感谢北京计算科学研究中心李俊、滑铁卢大学(University of Waterloo)鲁大为和多特蒙德大学(Technische Universität Dortmund)张竞夫在文章撰写过程中的讨论.

[1]Nielsen M A,Chuang I 2002Quantum Computation and Quantum Information(Cambridge:Cambridge University Press India)pp1–12

[2]Bennett C H,DiVincenzo D P 2000Nature404 247

[3]Deutsch D,Jozsa R 1992Proc.R.Soc.A439 553

[4]Shor P W 1994Proceedings of the 35th Annual Symposium on Foundations of Computer ScienceWashington,DC,USA,November 20–22,1994 p24

[5]Grover L K 1996Proceedings of the Twenty-eighth Annual ACM Symposium on Theory of ComputingPhiladelphia,USA,May 22–24,1996 p212

[6]Harrow A W,Hassidim A,Lloyd S 2009Phys.Rev.Lett.103 150502

[7]Li J,Peng X,Du J,Suter D 2012Sci.Rep.2 260

[8]Somaroo S,Tseng C,Havel T,Laf l amme R,Cory D G 1999Phys.Rev.Lett.82 5381

[9]Bennett C H,DiVincenzo D P,Smolin J A,Wootters W K 1996Phys.Rev.A54 3824

[10]Giovannetti V,Lloyd S,Maccone L 2011Nat.Photon.5 222

[11]Monz T,Schindler P,Barreiro J T,Chwalla M,Nigg D,Coish W A,Harlander M,Hänsel W,Hennrich M,Blatt R 2011Phys.Rev.Lett.106 130506

[12]Mariantoni M,Wang H,Yamamoto T,Neeley M,Bialczak R C,Chen Y,Lenander M,Lucero E,O’Connell A D,Sank D,Weides M,Wenner J,Yin Y,Zhao J,Korotkov A N,Cleland A N,Martinis J M 2011Science334 61

[13]Knill E,Laf l amme R,Martinez R,Tseng C H 2000Nature404 368

[14]Vandersypen L M,Steffen M,Breyta G,Yannoni C S,Sherwood M H,Chuang I L 2001Nature414 883

[15]Chuang I L,Vandersypen L M,Zhou X,Leung D W,Lloyd S 1998Nature394 143

[16]Jones J A,Mosca M,Hansen R H 1998Nature393 344

[17]Souza A M,Zhang J,Ryan C A,Laf l amme R 2011Nature Commun.2 169

[18]Zhang J,Yung M H,Laf l amme R,Aspuru-Guzik A,Baugh J 2012Nature Commun.3 880

[19]Negrevergne C,Mahesh T,Ryan C,Ditty M,Cyr-Racine F,Power W,Boulant N,Havel T,Cory D,Laf l amme R 2006Phys.Rev.Lett.96 170501

[20]Li J,Yang X D,Peng X H,Sun C P 2017Phys.Rev.Lett.118 150503

[21]Lu D,Li K,Li J,Katiyar H,Park A J,Feng G,Xin T,Li H,Long G,Brodutch A,Baugh J,Zeng B,Laf l amme R 2017 arXiv:1701.01198[quant-ph]

[22]Warren W S 1997Science277 1688

[23]Khaneja N,Reiss T,Kehlet C,Schulte-Herbrüggen T,Glaser S J 2017J.Magn.Reson.172 296

[24]Cory D G,Price M D,Havel T F 1998Physica D120 82

[25]Knill E,Chuang I,Laf l amme R 1998Phys.Rev.A57 3348

[26]Peng X,Zhu X,Fang X,Feng M,Gao K,Yang X,Liu M 2001Chem.Phys.Lett.340 509

[27]Ma X,Jackson T,Zhou H,Chen J,Lu D,Mazurek M D,Fisher K A,Peng X,Kribs D,Resch K J,Ji Z,Zeng B,Laf l amme R 2016Phys.Rev.A93 032140

[28]Gross D,Liu Y K,Flammia S T,Becker S,Eisert J 2010Phys.Rev.Lett.105 150401

[29]Maffei P,Elbayed K,Brondeau J,Canet D 1991J.Magn.Reson.95 382

[30]Freeman R,Morris G A 1978J.Magn.Reson.29 173

[31]Li J,Cui J Y,Yang X D,Luo Z H,Pan J,Yu Q,Li Z K,Peng X H,Du J F 2015Acta Phys.Sin.64 167601(in Chinese)[李俊,崔江煜,杨晓东,罗智煌,潘健,余琦,李兆凯,彭新华,杜江峰2015物理学报64 167601]

[32]Bauer C,Freeman R,Frenkiel T,Keeler J,Shaka A 1984J.Magn.Reson.58 442

[33]Warren W S 1984J.Chem.Phys.81 5437

[34]Wimperis S 1994J.Magn.Reson.Ser.A109 221

[35]Ryan C,Negrevergne C,Laforest M,Knill E,Laf l amme R 2008Phys.Rev.A78 012328

[36]Pan J,Cao Y,Yao X,Li Z,Ju C,Chen H,Peng X,Kais S,Du J 2014Phys.Rev.A89 022313

[37]Li J,Cui J,Laf l amme R,Peng X 2016Phys.Rev.A94 032316

[38]Levitt M H 2008Spin Dynamics:Basics of Nuclear Magnetic Resonance(England:John Wiley&Sons Ltd)pp93–99

[39]D’Ariano G,Presti P L 2001Phys.Rev.Lett.86 4195

[40]Zheng W,Yu Y,Pan J,Zhang J,Li J,Li Z,Suter D,Zhou X,Peng X,Du J 2015Phys.Rev.A91 022314

[41]Vandersypen L M,Chuang I L 2005Rev.Mod.Phys.76 1037

[42]Cory D G,Fahmy A F,Havel T F 1997Proc.Natl.Acad.Sci.USA94 1634

[43]Zhang J,Laf l amme R,Suter D 2012Phys.Rev.Lett.109 100503

[44]Boykin P O,Mor T,Roychowdhury V,Vatan F,Vrijen R 2002Proc.Natl.Acad.Sci.USA99 3388