船用低成本GNSS测向系统研究

戴邵武,刘 刚,王 朕,张文广,李瑞涛

(海军航空工程学院控制工程系,山东烟台 264001)

船用低成本GNSS测向系统研究

戴邵武,刘 刚,王 朕,张文广,李瑞涛

(海军航空工程学院控制工程系,山东烟台 264001)

GNSS导航星座主要由GPS、GLONASS、Galileo、BDS四大系统卫星组成,到2020年,用户有望同时观测到40多颗导航卫星,大幅提升导航性能的同时,也扩展了其应用领域。针对靶船、渔船对航向测量的需求,基于GNSS接收机应用现状,设计了低成本GNSS测向系统,使用2块Ublox LEA-M8T模块和STM32F407处理器搭建原理样机硬件平台,开展基于Kalman滤波器的载波相位差分姿态测量算法研究和基于Kalman滤波器的伪距差分姿态测量算法研究。静态实验表明,在8.5m基线的情况下,航向角测量标准差为0.0396°,俯仰角测量标准差为0.0889°。使用伪距差分算法,纬度方向上测量误差标准差为0.5923m,经度方向上测量误差标准差为0.4609m,高度方向上测量误差标准差为1.0766m。

全球导航卫星系统；载波相位差分；伪距差分；Kalman；测向

0 引言

舰船航向角定义为艏艉中心轴线在大地水平面上投影与当地真北方向的夹角,为舰船航行的重要参数。军用舰船和大型水面舰艇通常使用平台罗经和高精度惯性导航系统来测量舰船航向,具有精度高、完全自主、可靠性高、不容易受干扰等特点,但成本高、体积大,在渔船、靶船、巡逻船、商用货船等场合不适用[1]。

随着中国北斗卫星导航系统建设,2012年底,中国卫星导航系统管理办公室对外发布了《北斗卫星导航系统空间信号接口控制文件》,对外开放民用信号码结构,具备向亚太地区提供北斗卫星导航服务的条件,拉开了北斗应用市场的帷幕[2-4]。

早在2010年,中华人民共和国农业部发布了《北斗卫星导航系统渔业船载设备技术条件》的水产行业标准,规定60马力以上出海渔船安装北斗定位和通信系统,该系统对出海渔船的监控管理、抢险救助、灾害天气预警等起到了关键作用,但该系统只能测量渔船的位置,无法给出其航向信息,给渔船驾驶和监管带来不便。此外,自动靶船、测量船等无人航行器,迫切需要实现低成本的航向测量方案,以便实现按规划路线自主航行。

基于以上应用背景,本文设计了低成本的GNSS(Global Navigation Satellite System,全球卫星导航系统)船用测量系统方案,选用两款能输出原始观测量的商用GNSS模块,和GNSS天线、导航处理器组成GNSS测量系统,开展了硬件设计、软件设计和静态实验工作。

后续章节的安排是：第2部分介绍系统组成和硬件设计；第3部分介绍GNSS双天线测向算法及软件设计；第4部分开展静态实验研究；第5部分对本文工作进行总结。

1 测向原理及系统组成

受卫星轨道误差、卫星钟差、电离层误差、对流层误差、接收机钟差、多径误差等的影响,单天线GNSS定位精度为15m。将2个GNSS天线观测信号进行差分,消除上述误差后,能够实现厘米级的相对定位结果。双天线GNSS测向正是利用了上述原理,求得2个天线间的基线矢量,从而计算该基线矢量在地理坐标系中的航向角和俯仰角。基线矢量越长,则姿态角测量精度越高,典型情况下0.5m基线航向角精度为0.5°[7-8]。

GNSS通过伪码或载波相位实现距离测量,其中伪码测量精度为1m,而载波相位精度能达到2mm,但载波整周数无法测量,存在整周模糊度问题。如果GNSS两天线在卫星视线方向上距离不同,则接收到的GNSS载波相位不同,如图1所示。

图1 载波相位观测值Fig.1 Observation of carrier phase

两天线接收的载波相位差,即代表基线向量在卫星视线方向上的投影,通过观察3颗以上卫星的载波相位差,即可求解方程得到基线向量在ECEF(Earth-Centered, Earth-Fixed,地心地固)坐标系下的坐标,经过换算后即可得到航向角和俯仰角。

至此,GNSS测量的前提是能获得载波相位观测量,支持GNSS载波相位输出的商业模块主要包括Ublox公司M6T、M8T、M8P和东方联星公司CC50III模块,支持接收L1波段单频数据,价格均不超过1000元,各模块支持的系统如表1所示。

表1 各模块支持的GNSS系统

多GNSS系统带来更多的可视卫星数量,未来用户有望同时接收到40多颗卫星信号,冗余的卫星观测量将加快整数模糊度求解速度。因此,本文选用Ublox LEA-M8T模块来设计低成本GNSS测向系统,系统组成如图2所示。

图2 GNSS测向系统组成框图Fig.2 Block diagram of the GNSS heading determination system

导航处理器选用意法半导体公司的STM32F407芯片,主频达到168MHz,且具有单精度浮点运算单元,完全达到单频点GNSS测向软件需求,电路设计及实物如图3所示。

图3 电路设计及电路照片Fig.3 Designment and picture of electric circuit

该电路可使用USB接口进行供电,方便开展外场实验。

2 GNSS测向算法

本文以GPS L1和BDS B1频点为例来推导GNSS测向算法,但该算法很容易推广到Galileo E1和GLONASS G1频点使用[5-8]。GNSS伪距和载波相位观测值可表示为：

ρj,r=λ-1(rj,r+Ij,r+Tj,r)+f(δtr-δtj)+εj,r

(1)

ρj,b=λ-1(rj,b+Ij,b+Tj,b)+f(δtb-δtj)+εj,b

(2)

φj,r=λ-1(rj,r-Ij,r+Tj,r)+f(δtr-δtj)+Nj,r+ηj,r

(3)

φj,b=λ-1(rj,b-Ij,b+Tj,b)+f(δtb-δtj)+Nj,b+ηj,b

(4)

其中,ρ和φ代表伪距和载波相位(单位：周),λ为载波波长,r代表卫星到接收机的真实距离,I是电离层延迟,T是对流层延迟,f是载波频率,下标b代表base基准站,下标r代表rover移动站,下标j代表第j颗卫星,δtr是移动站接收机钟差,δtb是基准站接收机钟差,δtj是卫星钟差,N是整周模糊度,ε和η是伪距噪声和载波相位噪声,其方差可表示为卫星仰角的函数[9]

σ2=(a+b/sin2θ)/λ2

(5)

其中,θ是卫星仰角,a和b可以按照经验值选择,例如对于载波相位,可选择a=0,b=9e-6,而对于伪距,可选择a=0,b=2.25,即载波相位精度比伪距高500倍。

为了消除各项误差,首先进行基准站和移动站间差分：

ρj,rb=λ-1(rj,rb+Ij,rb+Tj,rb)+fδtrb+εj,rb

(6)

φj,rb=λ-1(rj,rb-Ij,rb+Tj,rb)+fδtrb+Nj,rb+ηj,rb

(7)

则可消除卫星钟差,再选择第i颗卫星为基准星,进行星间差分,得到双差观测量：

ρji,rb=λ-1(rji,rb+Iji,rb+Tji,rb)+εji,rb

(8)

φji,rb=λ-1(rji,rb-Iji,rb+Tji,rb)+Nji,rb+ηji,rb

(9)

可进一步消除接收机钟差,GNSS测向中通常2个天线距离较近,短基线情况下可忽略电离层和对流层误差：

ρji,rb=λ-1rji,rb+εji,rb

(10)

φji,rb=λ-1rji,rb+Nji,rb+ηji,rb

(11)

其中,ρji,rb是伪距双差观测量,φji,rb是载波相位双差观测量,均已知,Nji,rb是双差整周模糊度,rji,rb可表示为

rji,rb=-λ-1(aj,r-ai,r)Tbrb

(12)

其中,aj,r是接收机到第i颗卫星投影矢量,brb是基线向量,在ECEF坐标系表示为：brb=[xrbyrbzrb]。

2.1 载波相位差分算法

通过构造Kalman滤波器求解上述变量的浮点解,为了兼容GLONASS系统使用的FDMA调制方式,Kalman滤波选择单差整周模糊度为状态量,假设有m颗可视卫星,则状态向量为

X=[xrb,yrb,zrb,N1,rb,N2,rb,…,Nm,rb]

其状态转移矩阵为单位阵,则状态转移方程为

Xk+1=Fk,k+1Xk+Wk

(13)

Wk为状态噪声,其状态协方差矩阵Q中与基线相关的对角线元素取经验值,与单差模糊度相关的元素取为0。

Kalman滤波器观测量取为伪距双差和载波相位双差

Z=[φ1i,rb,…,φmi,rb,ρ1i,rb,…,ρmi,rb]=h(X)+V

观测矩阵H表示为：

(14)

Hbr=-λ-1[(a1,r-ai,r)T,…,(am,r-ai,r)T]T

(15)

(16)

第1颗卫星伪距双差观测噪声为(其余卫星类似计算)

(17)

上述是对单GNSS系统的滤波方程,如果同时观测GPS卫星和BDS卫星,由于存在GNSS系统间误差,无法共用基准星,所以需要在上述方程的基础上对矩阵进行增广,增加其维数即可,此处不再累述。

得到Kalman滤波器状态转移方程、观测方程、状态噪声矩阵、观测噪声矩阵后,可按以下步骤开展滤波：

Pk,k-1=Φk,k-1Pk-1(Φk,k-1)T+Qk-1

(18)

Kk=Pk,k-1(Hk)T[HkPk,k-1(Hk)T+Rk]-1

(19)

Pk=(I-KkHk)Pk,k-1

(20)

(21)

(22)

在每一个观测历元,当存在伪距观测量或载波相位观测量时,均进行Kalman滤波,可视卫星数量越多,则Kalman滤波收敛越快。例如,在野外开阔天空,使用GPSL1频点和BDSB1频点接收机,则通常单历元即可求得较准确的基线矢量、单差整周模糊度浮点解。

获得单差模糊度浮点解Nfloat及其状态协方差矩阵PSD后,通过矩阵D转换为双差模糊度浮点解DNfloat及其方差阵DPSDDT,便可利用标准的Lambda算法搜索双差模糊度整数解,双差模糊度整数解固定后,便可计算得到高精度的基线向量[10]

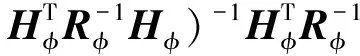
(23)

其中,Xr为移动站单点定位坐标,Xb为基准站单点定位坐标,Hφ是与载波相位相关的观测子矩阵,Rφ是载波相位观测噪声,φm,DD是双差载波相位观测值列向量, N是双差整周模糊度,当双差模糊度整数解固定后,将整数解带入计算,否则,带入浮点解计算。

此外,开源rtklib软件运行载波相位差分算法时,当增加可视卫星数时,会导致Kalman滤波误差增大,进一步导致双差模糊度整数解无法固定。针对这一问题,本文在新增加卫星观测量时,先根据当前基线计算结果,解方程求其模糊度整数解,之后再加入Kalman滤波中,在短基线情况下有效解决了上述问题。

2.2 伪距差分算法

载波相位差分算法能达到厘米级的测量精度,然而,当可视卫星数量较少,或者卫星信号载噪比小于38dBHz的情况下,由于载波相关观测量少或观测精度不高,将导致载波相位差分算法失效。此时,伪距差分可以作为替代方案。

伪距差分算法能达到米级测量精度,由于船体长度通常为30～100m之间,将天线分别布置在船艏和船艉,如果伪距差分算法精度为1m,天线基线长度为70m,则航向角精度为1/70=0.0143rad,约为0.8185°,满足舰船驾驶需求。

同样使用Kalman滤波器实现伪距差分算法,其实现过程与载波相位差分算法类似,只是去除与载波相位相关的部分即可,此处不再累述。

3 静态实验

为了验证本文设计GNSS测向系统精度,使用硬件系统开展了静态实验工作。实验时间为2016年5月14日10：00～16：00,实验地点为山东烟台海军航空工程学院综合实验楼楼顶,使用2个NovatelGPS701-GG测量型天线,天线间的距离为8.5828m。

本文设计的GNSS测向算法只使用GPS和BDS卫星信号,实验过程中,可视卫星数量如图4所示。

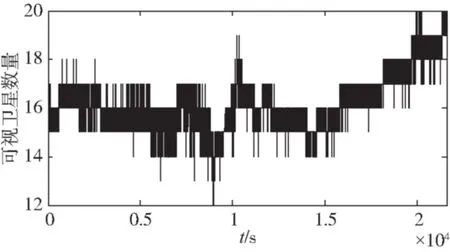
图4 可视卫星数量Fig.4 Number of used satellites

整个实验过程中,载波相位差分算法双差模糊度整数解均保持锁定(阈值为2)。基线长度、航向角、俯仰角测量值如图5～图7所示。

图5 基线长度测量值Fig.5 Length measurement of baseline

图6 航向角测量值Fig.6 Measurement of heading angle

图7 俯仰角测量值Fig.7 Measurement of pitch angle

其中,基线向量测量标准差为5.2mm,航向角测量均值为351.269°,标准差为0.0396°,俯仰角测量均值为-0.2322°,标准差为0.0889°。此处为8.5828m基线的测量结果,在船上增长基线的情况下,姿态测量精度更高。

为了验证伪距差分的性能,利用实验过程中采集的原始观测量,进行事后伪距差分处理,得到在纬度、经度、高度方向上测量误差曲线如图8所示。

图8 伪距差分测量误差Fig.8 Measurement error of RTD

其中,纬度方向上误差标准差为0.5923m,经度方向上误差标准差为0.4609m,高度方向上误差标准差为1.0766m。如果在船上基线长度能达到70m以上,则通过伪距差分测量的航向角精度能达到0.5°以内(参见2.2节),可以作为备选测量方案,在恶劣场景中使用。

4 结论

本文针对靶船、渔船等中型舰船对航行姿态测量的需求,设计了基于UbloxLEA-M8T模块和STM32F407处理器的低成本GNSS测向系统。一方面,搭建了原理样机硬件平台,将2块UbloxLEA-M8T模块原始观测量输入到STM32F407处理器,处理器内部经过软件处理后直接输出姿态测量值；另一方面,开展了基于Kalman滤波器的载波相位差分姿态测量算法研究和基于Kalman滤波器的伪距差分姿态测量算法研究。静态实验表明,在8.5m基线的情况下,航向角测量标准差为0.0396°,俯仰角测量标准差为0.0889°。使用伪距差分算法,纬度方向上测量误差标准差为0.5923m,经度方向上测量误差标准差为0.4609m,高度方向上测量误差标准差为1.0766m。

[1] 阎肖鹏,王海涛. 基于两台双天线GPS测向单元的靶船测姿方法 [J]. 舰船电子工程, 2012, 32(5):65-67.

[2] 谢钢.GPS原理与接收机设计 [M]. 北京:电子工业出版社, 2009.

[3] 谢钢. 全球导航卫星系统原理:GPS、格洛纳斯和伽利略系统 [M]. 北京:电子工业出版社, 2013.

[4]ChinaSatelliteNavigationOffice.BeiDounavigationsatellitesystemsignalinspaceinterfacecontroldocumentopenservicesignal(Version2.0) [M].Beijing:ChinaSatelliteNavigationOffice, 2013.

[5]OdolinskiR,TeunissenPJ,OdijkD.CombinedBDS,Galileo,QZSSandGPSsingle-frequencyRTK[J].GPSSolution, 2015, 19(1):151-163.

[6]ZhaoS,CuiX,FengG,etal.AKalmanfilter-basedshortbaselineRTKalgorithmforsingle-frequencycombinationofGPSandBDS[J].Sensors, 2014, 14(8):15415-15433.

[7] 刘海颖,王嘉南,陈志明. 卫星导航原理与应用 [M]. 北京: 国防工业出版社, 2013.

[8] 王冰. 基于GNSS的实时姿态确定算法研究 [D]. 郑州: 解放军信息工程大学, 2013.

[9]TakasuT.RTKLIBver. 2.4.2Manual[M].Tokyo:TokyoUniversityofMarineScienceandTechnology, 2013.

[10]TeunissenPJG.Theleast-squareambiguitydecorrelationadjustment:amethodforfastGPSambiguityestimation[J].JournalofGeodesy, 1995, 70(1):65-82.

Research on Low-cost GNSS Heading Determination System for Ship

DAI Shao-wu, LIU Gang, WANG Zhen, ZHANG Wen-guang, LI Rui-tao

(Department of Control Engineering, Naval Aeronautical and Astronautical University, Yantai,Shandong 264001, China)

Global Navigation Satellite System consists of GPS, GLONASS, Galileo and BDS satellites. Customers will have been able to receive signals from more than 40 satellites by 2020, which would lead to great improvements of GNSS performance and the extension of its application fields. Based on the actual utility situation of GNSS receiver, and in order to determine the heading of the target ship and fishing fleet, this paper designs a low-cost GNSS heading determination system. Firstly, prototype hardware platform is designed using two Ublox LEA-M8T modules and a STM32F407 ARM MCU. Secondly, researches on real time kinematic and real time differential algorithms based on Kalman Filter method are carried out. Finally, static test results show the flowing performances: using 8.5m baseline, the standard deviation of yaw and pitch are 0.0396° and 0.0889° respectively with real time kinematic algorithm. The standard deviation of measurement along latitude, longitude, height are 0.5923m, 0.4609m and 1.0766m respectively.

Global Navigation Satellite System; Real time kinematic; Real time differential; Kalman; Heading determination

2016-07-25；

2016-08-30

国家自然科学基金(61473306)

戴邵武(1966-),男,博士,教授,主要研究领域为导航、制导与控制。E-mail:daiswhy@163.com

10.19306/j.cnki.2095-8110.2017.02.009

U666.134

A

2095-8110(2017)02-0048-05