并行级联卷积码基于软输入硬输出的迭代译码

彭万权

(重庆工程职业技术学院，重庆 江津，402260)

并行级联卷积码基于软输入硬输出的迭代译码

彭万权

(重庆工程职业技术学院，重庆 江津，402260)

以递归卷积系统码为分量码构造的并行级联卷积码具有优良的距离特性，本文提出一种新的迭代译码算法，通过引入校正因子α(n)和β(n)，对viterbi译码输出和原始接收信息进行线性叠加，从而将当前的硬判决译码输出转化为下一次译码的软输入。仿真结果表明，该算法与乘积码相比，具有更强的纠错性能和更快的译码速度。

递归系统卷积码；并行级联卷积码；迭代译码；校正因子

Turbo码[1]也称并行级联卷积码(PCCC)，其基本思想在于将卷积码和交织器相结合，用随机编码策略巧妙地实现了长码。为了达到行与列的交织，以及获得良好的距离特性，其分量码采用了一种特殊类型的卷积码——递归卷积系统码，Turbo码译码器的一个重要组成部分是软输人硬输出器，它能够为下一级译码提供外信息，从而实现多次迭代译码，获取外信息的经典算法包括MAP和SOVA[2]，其中MAP算法的性能能够逼近Shannon限，但复杂的计算致使其硬件实现非常困难；SOVA算法性能比MAP差，但仅仅两倍于Viterbi的运算量使其更适合于工程运用。目前很多turbo码迭代译码基本都是围绕MAP、SOVA算法进行，并在各种通信系统中广泛应用。

当采用分组码作为级联码的分量码时可称之为乘积码[3]，作者曾在文献[4]中针对该码型提出一种简化算法。虽然乘积码与本文PCCC在构造方式上存有一定区别，但其叠加反馈的迭代译码算法是可以借鉴的：在反馈时纳入了两个校正因子α(n)和β(n)，分量码译码器通过Viterbi译码输出硬判决信息，并借助校正因子与接收软信息进行线性处理，从而得到下一级译码器的软输入。由于本算法在获取外信息时与标准viterbi算法的复杂度相当，仅为SOVA算法的一半，因此在工程上具有一定的实用价值。文章主要阐述算法的编译码原理，仿真部分给出了不同情况的测试结果，并在计算速度和纠错性能等方面与乘积码进行了比较。

1 PCCC的编码

1.1 分量码的编码

卷积码类似于连环锁链的编码构造策略体现了不同时刻码组之间的信息共享，具有良好的距离特性，是级联码分量码的较佳选择。但是，级联码的构造特点决定了其分量码必须为系统码，而传统系统卷积码的纠错性能又明显逊于非系统卷积码，因此在PCCC中必须纳入一种递归系统卷积码(RSC)[5]。递归系统卷积码是一种带反馈的编码器，可以由非系统卷积码从编码输出端向输入端引入反馈而得，图1是码率=0.5、约束长度=4的(23，35)RSC编码器。其生成矩阵为

(1)

其中D为延迟算子，表示编码过程中一个单位时间的延迟。RSC既是一种系统码，又具有和非系统卷积码同样出色的纠错能力，因此很好地解决了如何选择PCCC分量码的问题。

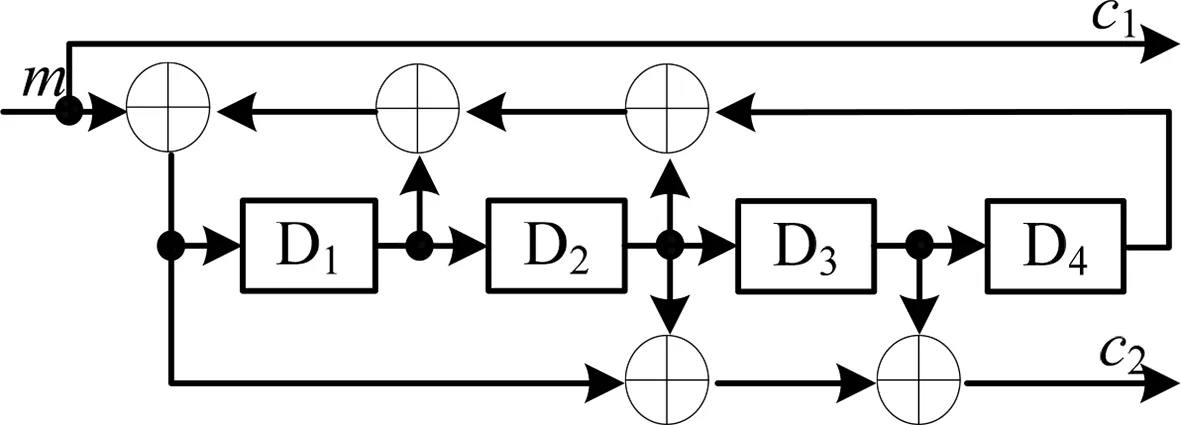
图1 (23，35)RSC编码器Fig.1 (23，35)RSC encoder

1.2 PCCC的编码

PCCC编码器如图2所示，k1×k2位信息序列矩阵M经过一个行进列出交织器，形成一个新的序列MT，二者分别传送到两个相同的RSC分量码编码器。为了使矩阵复接后码率依然等于0.5，还需对分量码编码器的输出进行删余处理，删余矩阵为

(2)

其中第一行或第二行分别表示按奇数位置或偶数位置间隔保留行或列卷积码的校验位，设信息块、行校验块和列校验块矩阵分别为Cm、Cr、Ca，按顺序复接后得到编码输出矩阵为

C=[CmCrCa]

(3)

该码字矩阵的比特数为k1×k2+0.5k1×k2+k1×0.5k2=2k1×k2，可见其编码码率为1/2。

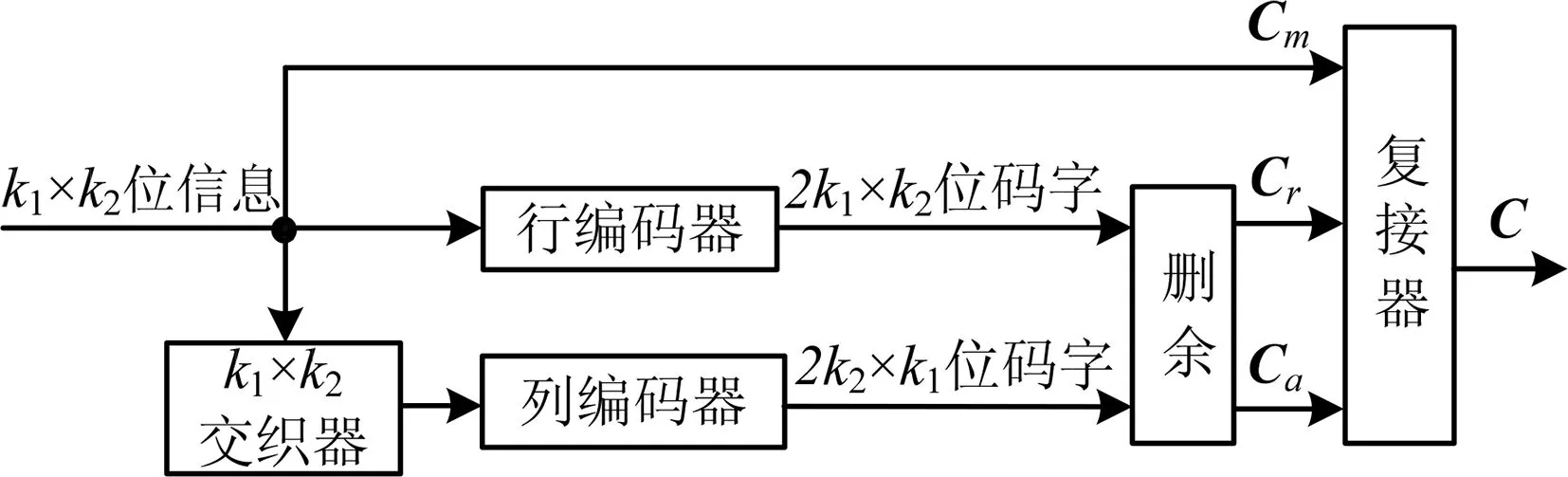
图2 PCCC编码器框图Fig.2 PCCC encoder frame diagram

2 PCCC的反馈迭代译码

Viterbi译码作为一种经典算法，几乎适用于任意类型的卷积码[6-7]，其主要基于码的网格图，通过乘-加比选操作寻找一条具有最佳估计值的路径。该算法所具有的一个显著优势是，其软判决译码和硬判决译码的复杂度近乎相等，因此特别适合对PCCC进行译码。

图3为并行卷积级联码的反馈迭代译码器，采用串行方式，每一次迭代包含两次viterbi译码、复接和交织等操作，若干次迭代构成整个译码器。设码阵C经过BPSK调制和高斯信道，在接收端接收到带有噪声的软信息矩阵为:

R=E+G=[RmRrRa]

(4)

图3 PCCC的串行译码器Fig.3 PCCC serial decoder

(5)

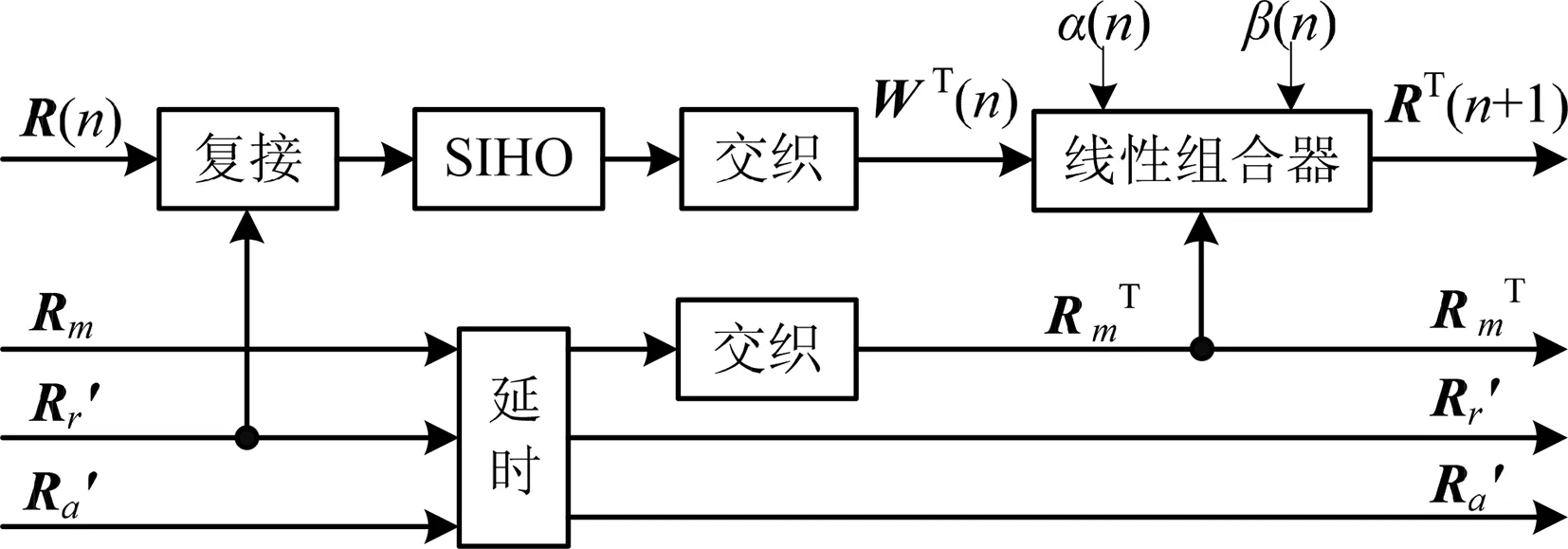
图4 半个迭代过程Fig.4 Semi iterative process

3 仿真实验

实验在BPSK和高斯信道环境下进行，选用以(1)式为生成多项式的(2，1，4)RSC作为分量码，为了进一步降低译码复杂度，本文采纳了文献[7]相关研究成果，对分量码实施Viterbi的矩阵化译码。 viterbi译码的幸存路径存储长度为30，并在发生2000～10000bit错误时终止仿真。实验的首要任务是确定出合适的α(n)和β(n)序列，设α(n)和β(n)序列是尾数和首数分别为1的递增等差数列。当信噪比Eb/No=2.2dB、交织长度N=64×64、迭代次数=4时，经大量测试，发现α(n)=(0.3，0.4，0.5，0.6，0.7，0.8，0.9，1)、β(n)=(1，1.1，1.2，1.3，1.4，1.5，1.6，1.7)近乎为最佳的序列组合。

采用行进列出交织方式时，PCCC对交织器行数与列数的选择比乘积码更为灵活，原则上可选用任意偶数行或偶数列。图5是迭代四次，交织长度分别为10×10、20×20、32×32和44×44时的误码特性对比。由该图可以看出交织长度对译码性能有着直接的影响，但交织长度变得足够大时，这种影响将逐渐减弱。

图5 不同交织长度的误码特性Fig.5 Error characteristics of different interleaving lengths

结合文献[3]和[4]，图6给出了(64，45，8)2乘积码与PCCC的信噪比误码率关系曲线对比，鉴于可比性，均采用四次迭代，PCCC的交织长度选为44×44，此时两种码型具有非常接近的块长度和编码效率，如表1所示。该图表明在中低信噪比时PCCC具有更强的纠错能力，考虑到10-5的误码率能满足一般的工程要求，即便PCCC存在底板效应也无疑为更好选择。表1还给出了二者的仿真速度，之所以PCCC在计算速度上更具优势，主要原因在于viterbi软判决译码比chase2译码效率更高。

图6 乘积码和PCCC的误码特性对比Fig.6 BER comparison between product codes and PCCC

分量码帧长度编码效率计算速度(2,1,4)1936bit0.529Mbit/s(64,45,8)2025bit0.4944.5Mbit/s

4 结论

本文采用viterbi算法对PCCC的分量码进行译码，虽然得到的是硬判决输出，但是通过利用迭代过程中这种硬判决输出的可信度逐渐增强的特点，与原始的接收软信息进行线性叠加，从而获得了下一次译码的软输入，校正因子的引入有效地控制了已译信息的再利用程度。仿真实验确定出α(n)和β(n)序列，并对不同迭代次数和不同交织长度进行了测试，最后与参数条件相似的乘积码进行比较，发现PCCC在纠错能力和译码速度上占有明显优势。

[1]C BERROU，A GLAVIEUX.Near optimum error-correcting coding and decoding:turbo codes [J].IEEE Transaction on Communications,1996,44(10):1261-1271.

[2]Jinyoung Kim，Jaejin Lee.Iterative Two-Dimensional Soft Output Viterbi Algorithm for Patterned Media[J].IEEE Transactions on Magnetics ，2011，47(3):594 - 597.

[3]党小宇，陶静，虞湘宾，等.一种低复杂度Turbo乘积码自适应Chase译码算法[J].电子与信息学报，2014，36(3):739-743.

[4]彭万权，冯文江.乘积码基于相关运算的迭代译码[J].电路与系统学报，2006，11(4):26-30.

[5]张立民，刘杰，钟兆根.(n,1,m)递归系统卷积码的盲识别[J].电讯技术，2014，54(9):1220-1225.

[6]彭万权，张承畅，冯文江，等.多阶幻方卷积码的构造及译码[J].电子学报，2013，41(1):123-130.

[7]彭万权，伍小兵，张承畅.一种维特比译码器的矩阵实现方案[J].电路与系统学报，2012，17(3):115-120.

Iterative decoding of parallel concatenated convolutional codes based on soft input hard output

PENG Wanquan

(Chongqing Vocational Institute of Engineering，Chongqing 402260，China)

Parallel concatenated convolutional codes constructed with recursive system convolutional codes as component codes have good distance characteristic. This paper presents a new iterative decoding algorithm, by introducing correction factorα(n) andβ(n), the viterbi decoding output and the original received information are linearly superimposed, and the current hard decision decoding output is converted into the soft input of the next decoding. The simulation results show that this algorithm has better error correcting performance and faster decoding speed than the product code.

recursive systematic convolutional code; parallel concatenated convolutional codes; iterative decoding; correction factor

1672-7010(2017)02-0023-05

2017-02-24

重庆市基础与前沿研究计划项目(cstc2013jcyjA40055 )

彭万权(1974-)，男，重庆垫江人，副教授，硕士，从事纠错码的算法研究工作

TN911.22

A