复杂组合结构振动试验的有限元-统计能量混合建模与分析
张永杰,陈 璐,王 喆,秦朝红
(北京强度环境研究所,北京,100076)
复杂组合结构振动试验的有限元-统计能量混合建模与分析
张永杰,陈 璐,王 喆,秦朝红
(北京强度环境研究所,北京,100076)
对某一梁板组合结构进行振动台试验,并对该结构振动试验进行有限元-统计能量(FE-SEA)混合建模分析,将梁板组合结构与振动台工装连接的梁建立为环形梁统计能量子系统,从而对其施加约束来实现振动台加速度载荷的施加。分析了内声腔以及外部空气对结构振动的影响,并将有限元-统计能量(FE-SEA)混合模型计算结果与试验结果进行了对比分析。结果表明,梁板组合结构振动试验的FE-SEA混合模型计算结果与试验结果基本吻合,验证了使用H-混合模型方法进行梁板组合结构振动分析的有效性。
梁板组合结构;振动试验;有限元-统计能量混合模型
0 引 言
在航天器中普遍存在梁板组合结构,由于结构的子系统间存在显著的动态特性差异,从而导致航天器在受到发动机脉动推力作用下的振动响应预示变得复杂和困难。由于梁板子结构间存在较大的动态差异,使得在比较广泛的频率区间,梁板组合结构的振动表现为梁结构上的局部长波变形和板结构上的局部短波变形的情况,这就产生了典型的系统中频振动情况[1,2]。
H-混合模型法(Hybrid FE-SEA method)是目前常用的梁板组合结构中频振动分析理论方法[3~5]。该方法的原理为:将梁板组合结构视为由确定性子结构和非确定性子结构组成,对其中的确定性子结构采用有限元模型来描述,而其余子结构使用统计能量模型来描述,从而建立有限元-统计能量(FE-SEA)混合模型。在梁板组合结构的振动试验中,振动台对结构施加力,但是施加在结构上的力很难直接测量得到,只能得到振动台表面及结构上的振动加速度。在有限元计算方法中,一般使用“大质量”法解决基础激励的加速度载荷施加问题[6,7]。而在FE-SEA混合模型方法中,统计能量子系统的求解变量为子系统的功率,如何对基础激励进行建模与分析则需要进行深入的研究。
对某一梁板组合结构进行了振动台试验,并对该结构振动试验进行了 FE-SEA混合建模分析,将梁板组合结构与振动台工装连接的梁建立为环形梁统计能量子系统,从而对其施加约束来实现振动台加速度载荷的施加。分析了内声腔以及外部空气对结构振动的影响,并将 FE-SEA混合模型计算结果与试验结果进行了对比分析。
1 梁板组合结构振动试验
1.1 结构几何模型
某一典型的梁板组合结构如图1所示,整个结构由矩形截面箱梁和不同厚度的薄板组成。梁与板之间通过铆钉和螺钉连接,从而形成一个完整的梁板组合结构。板通过螺钉和铆钉连接在梁上。矩形截面箱梁横截面尺寸为3 cm×3 cm,厚度为3 mm。7块板的厚度如表1所示,图1中梁22和梁23均为测点位置。整个梁板组合结构长为1.4 m,宽为 1.0 m,高为0.8 m,梁与板的材料均为Q235钢。
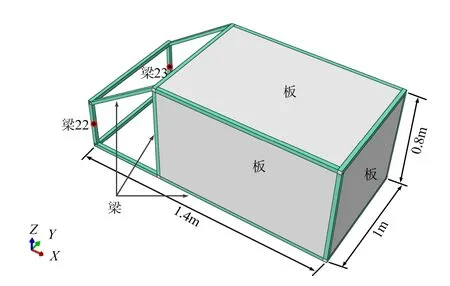
图1 某典型梁板组合结构

表1 梁板组合结构中各板的厚度
1.2 振动试验
将该梁板组合结构固定于振动台上进行振动试验,试验状态如图2所示。

该结构一端的4根梁固定于振动台上的工装上,振动通过4根竖立的梁传递到上部的板以及其它梁。在振动台工装表面、与工装相固定的梁上布置振动加速度传感器,在该梁板组合结构的每块板上均匀分布5~7个振动传感器。振动台按设置的一定量级的输入条件振动,待梁板组合结构的振动响应稳定后,采集各传感器数据用于分析。通过试验可以获取不同振动台输入量级下的整个结构上梁与板的振动响应数据。
2 FE-SEA混合建模
在该梁板组合结构中,梁结构和板结构动态特性差异较大,两者之间动态特性差异主要表现在波数比上。对于梁子结构,其横向弯曲振动的波数与材料属性和横截面形状有关,对于板子结构,其横向弯曲振动的波数与材料属性和厚度有关。图 3为该梁板组合结构中梁和两种不同厚度薄板的波数,由图3可以看出,在10~2 000 Hz分析频率范围内,1.5 mm厚板的波数最小值均在5个/m以上,而梁的波数在16 Hz时仅为1个/m左右,1.5 mm和1 mm厚度的板波数与梁的波数之比分别为5和6,这说明在整个分析频率范围内该结构中梁子结构的动态特性差异非常大,因此可以将梁子结构视为确定性子结构,而板视为非确定性子结构。对确定性子结构使用有限元方法建模,对非确定性子结构使用统计能量方法建模,从而在VA One软件中建立该系统的有限元-统计能量(FE-SEA)混合模型。各板的厚度和材料参数分别如表1和表2所示。
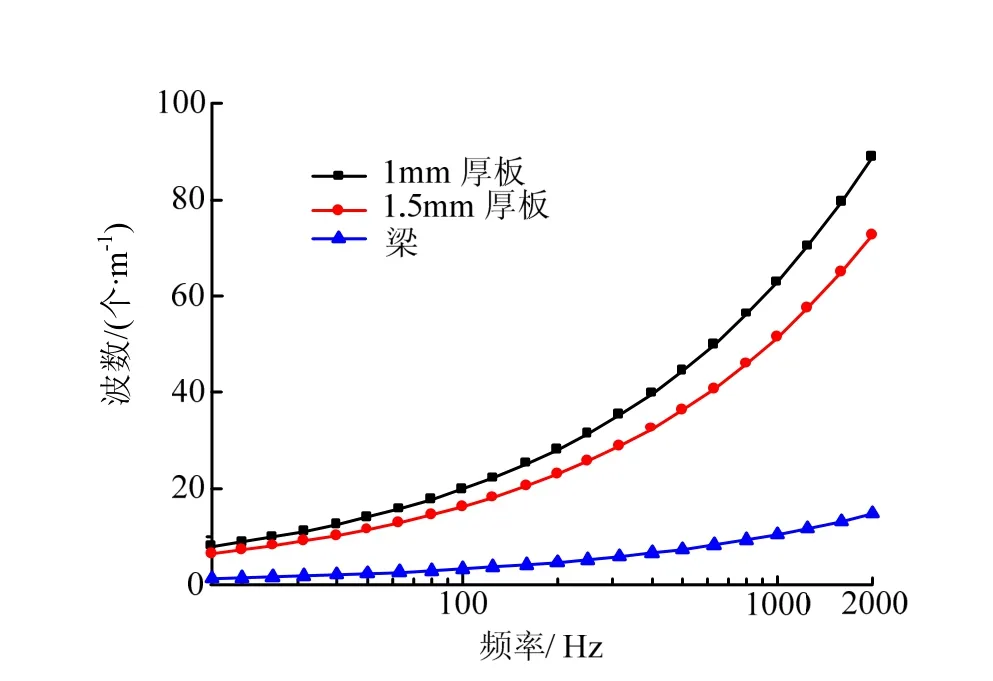
图3 梁和两种不同厚度薄板的波数比

表2 模型材料参数
振动台加速度载荷通过统计能量子系统的约束施加,因此需要将该梁板组合结构与振动台工装连接的梁建立为环形梁统计能量子系统。对该梁板组合结构建立的整个FE-SEA混合模型如图4所示。整个模型中包含8 656个有限元节点和8个统计能量子系统,相比较整个梁板组合结构全部使用有限元方法来建模,FE-SEA混合模型大大减少了计算量。

图4 梁板组合结构的FE-SEA混合模型
3 计算结果分析
振动台输入控制条件中均方根(Root Mean Square, RMS)值为1.7 g时,试验中振动台控制点的功率谱密度以及与工装固定梁的振动加速度(图1所示梁22、梁23位置)功率谱密度(Power Spectral Density, PSD)曲线如图5所示。振动台控制点功率谱密度与固定梁的振动加速度功率谱密度谱形完全不同,均方根值也相差很大,梁上的加速度均方根值约为振动台控制点加速度均方根值的3倍。而两个固定梁上的加速度功率谱密度谱形相似,因此平均后作为 FE-SEA混合模型中对Ring beam统计能量子系统的约束载荷。

图5 振动台控制点及固定梁的加速度功率谱密度曲线
模型分析频率范围设为16~2 000 Hz之间。模型响应计算结果如图6所示,图6a为模型加速度响应计算结果,整个模型中振动量级最大的位置处于斜支撑的两根梁中部,达到了近18 g。为了分析内声腔以及外部空气对结构振动的影响,在模型中建立内声腔,并在外部连接半无限流体统计能量子系统来模拟空气的影响,计算结果如图6b所示,可以看出在16~2 000 Hz分析频率内,空气对该结构的振动表现为轻微的能量耗散,对振动均方根值影响可以忽略不计,而如果分析频率大于板的临界频率(板的弯曲波速等于声波速时对应的频率)时,则需要考虑空气对板振动的影响。

图6 计算结果
模型中的7块板的振动加速度功率谱密度计算与试验结果比较如图7所示。由图7可知计算结果与试验结果基本吻合,功率谱密度在500 Hz以内相差较大,而在500 Hz以外计算结果能够反映实际振动的峰值特点。各板均方根值的计算与试验结果对比如图8所示。7#板振动量级最小,1#、2#板振动量级最大,均方根值误差最大为 3.9 dB,最小为 0.5 dB,满足工程上±6 dB的精度要求。3#板的模型计算值比试验值高说明当薄板面积较小时,多个传感器的质量对板的响应影响较大。考虑到板件与梁的连接为距离不规则的螺钉和铆钉,以及由于加工装配误差等导致板件安装状态下并非是理想平面等随机因素,要想获取更精确的计算结果,则需要通过试验来获取模型中的模态密度、内损耗因子、耦合损耗因子等参数。
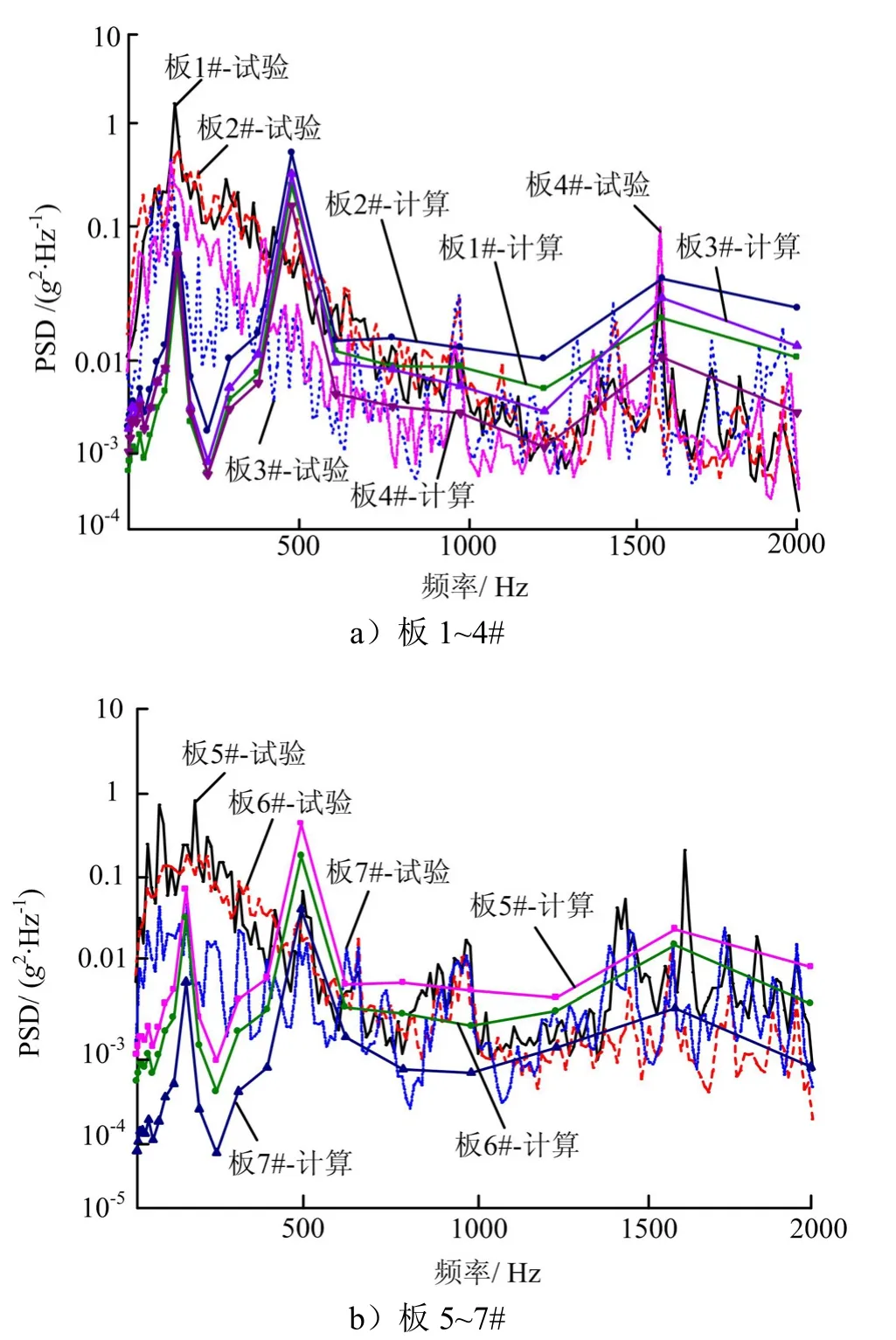
图7 各板振动功率谱密度计算与试验结果比较
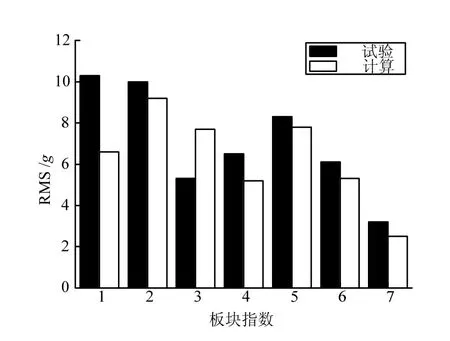
图8 各板振动均方根值计算与试验结果比较
4 结 论
对某一典型梁板组合结构进行了振动台试验,并建立了 FE-SEA混合模型进行分析,使用约束载荷解决了振动台加速度载荷的施加问题。通过对模型计算结果和试验结果的比较分析,得到如下结论:
a)在10~2 000 Hz范围内,1 mm和1.5 mm厚度的薄板与梁的动态特性差异非常大,将确定性子结构梁用有限元分析方法表示,非确定性子结构薄板用统计能量分析方法表示,建立的 FE-SEA混合模型中节点数目减少,提高了运算速度。
b)振动台控制点与固定梁的振动加速度功率谱密度谱形完全不同,均方根值也相差很大,而与工装固定的梁上的加速度功率谱密度谱形相似。将梁板组合结构与振动台工装连接的梁建立为环形梁统计能量子系统,则振动台加速度载荷可通过统计能量子系统的约束施加。
c)该结构中板的临界频率在2 000 Hz分析频率以上,因此空气对板的振动表现为轻微的能量耗散,对分析频率范围内的振动均方根值影响可以忽略不计。而如果分析频率大于板的临界频率时,则需要考虑空气对板振动的影响。
d)梁板组合结构振动试验的FE-SEA混合模型计算结果与试验结果基本吻合,均方根值误差最大为3.9 dB。验证了使用H-混合模型方法进行梁板组合结构振动分析的有效性。考虑到板件与梁的复杂连接,以及由于加工装配误差等因素,要想通过 FE-SEA混合模型得到更精确的预示结果,则需要通过试验来获取模型中各子结构的内损耗因子、模态密度等参数。
[1]Zhao X, Vlahopoulos N. A basic hybrid finite element formulation for mid-frequency analysis of beams connected at an arbitrary angle[J]. Journal of Sound and Vibration, 2004, 269(6): 135-164.
[2]纪琳. 中频振动分析方法[M]. 北京: 机械工业出版社, 2013.
[3]Langley R S, Bremner P. A hybrid method for the vibration analysis of complex structural-acoustic systems[J]. Journal of the Acoustical Society of America, 1999, 105(3): 1657-1671.
[4]Shorter P J, Langley R S. Vibro-acoustic analysis of complex systems[J]. Journal of Sound and Vibration, 2005, 288(3): 669-699.
[5]张瑾, 邹元杰, 韩增尧. 声振力学环境预示的FE-SEA混合方法研究[J].强度与环境, 2010, 37(03): 14-20.
[6]周国良, 李小军, 刘必灯, 等. 大质量法在多点激励分析中的应用、误差分析与改进[J]. 工程力学, 2011, 28(01): 48-54.
[7]Kim Y W, Jhung M J. A study on large mass method for dynamic problem of multiple degree-of-freedom system excited by ground acceleration time history[J]. Journal of Mechanical Science & Technology, 2014, 28(1): 25-41.
Research on Hybrid FE-SEA Method for Vibration of Complex Built-up Structure
Zhang Yong-jie, Chen Lu, Wang Zhe, Qin Zhao-hong
(Beijing Institute of Structure and Environment Engineering, Beijing, 100076)
A hybrid FE-SEA model of a beam-plate built-up structure is developed for response prediction in vibration testing. The acceleration loads are applied to the model. The influence of the ambient air on the response of the structure is analyzed. The results obtained by the model and experiments are compared. The hybrid FE-SEA method is reliable for the mid-frequency vibration problems of the beam-plate built-up structure.
Beam-plate built-up structure; Shaking table experiment; Hybrid FE-SEA method
V214.3
A
1004-7182(2017)01-0093-04
10.7654/j.issn.1004-7182.20170122
2015-11-20;
2015-12-30;数字出版时间:2017-01-24;数字出版网址:www.cnki.net
张永杰(1983-),男, 博士,高级工程师, 主要研究方向为结构动力学

