非饱和土双应力变量广义土水特征曲线理论模型构建

汪时机，程明书，李 贤,2，王晓琪，毛 新，杨惠迪



非饱和土双应力变量广义土水特征曲线理论模型构建

汪时机1，程明书1，李 贤1,2，王晓琪1，毛 新1，杨惠迪3

（1. 西南大学工程技术学院，重庆400715；2. College of Physical Sciences & Engineering, Cardiff University, CF243AA, UK；3. 湖南大学土木工程学院，长沙410082）

土水特征曲线（soil-water characteristic curve，SWCC）方程是非饱和土力学中最重要的土性表征手段之一。该文评价当前经典的SWCC方程，指出其未具有包容复杂因素的能力，具有灵活性的优点但却同时具有对试验数据量依赖性高的缺点，不能处理多孔隙尺度集群土体固-液-气共同运动及作用的水力-力学耦合效应问题。建立双应力变量广义SWCC概念图示并定义相对体积含水比，基于Fredlund双应力变量理论及van Genuchten土-水表征方程，构建考虑土体变形及多孔隙分布形态的双应力状态变量的广义SWCC方程。相较于2个参数的Brooks等的方程、3个参数的van Genuchten方程以及4个参数的Fredlund等的方程，广义SWCC方程仅3个参数，其中2个参数在双对数坐标系的“相对体积含水比-吸力”平面中进行最小二乘法线性拟合得到，仅1个参数需非线性最小二乘法拟合得到。该模型可利用不同应力状态下的至少3个土水试验数据点，绘制出1条具有适宜精度的单峰SWCC；方程考虑了多峰孔隙概率密度函数分布及土体变形因素，实现了从应力历史推广到应力状态的广义情况，为定量描述不同孔隙结构土体双应力状态下的持水特性、渗透特性和强度特性提供了一条途径。

土壤水分；应力；模型；持水特性；非饱和土；土水特征曲线；双峰SWCC

0 引 言

非饱和土壤是由固-液-气组成的可变形、可压缩的多相地质体[1-2]，持水状态的不同，是造成土壤变形、强度、渗透性差异的重要原因[3-5]；同时，土壤受本身的孔隙结构形态、分布以及应力状态的影响，具有较一般材料复杂的水力-力学性质。这种复杂性的重要成因是由土壤孔隙中的水体（重力水、毛管水、吸附水、薄膜水）随吸力（=u−u，为孔隙气压、u为孔隙水压）的变化进入新的耦合平衡状态及形成复杂的土-水结合系统（水封闭、双开敞、气封闭系统[6]）造成。吸力和持水量（饱和度S、质量含水量或体积含水量）之间的曲线关系定义为土水特征曲线（soil-water characteristic curve，SWCC）[7-9]。土壤学上，利用土性估算土壤水力性质（包括SWCC）的曲线方程亦称作土壤转换函数（pedotransfer functions，PTFs）[8]。SWCC模型是定量表征土-水关系的核心，已被广泛用于研究土壤持水能力[10]、渗透特性[9,11]、土壤结构稳定性[12]、颗粒大小分布[13]及抗剪强度[14]，有着广泛的应用需求[15-16]。

自20世纪60年代以来，van Genuchten[11]提出了一系列的SWCC表征方程，对土-水关系进行定量表征。这些研究多是基于吸力变化过程中土体零体变、孔隙结构连续假定的情形。由于土体的多相、可压缩特点，在净法向应力及吸力作用下，会产生不可忽略的变形。Fredlund等[17]基于多相连续介质力学从理论及试验上证明了土壤固-液-气三相介质实际上受净法向应力（=–u，为竖向压力）和吸力2个变量的控制。及被看作是建立非饱和土本构模型的2个关键的独立应力状态变量[17-18]，为定量研究土壤持水、渗透、变形和强度提供了严谨的理论支撑[17,19]。

直到最近，Gallipoli等[20-22]开始考虑土体变形的SWCC以及多峰孔隙密度分布函数（multimodal pore-size density probability distribution function，M-PDF）的情形。当前，应力引起土体变形的研究可分为吸力[23]、正应力[16,20]及二者耦合引起土体变形3类[24]。由于传统SWCC量测极为耗时，动辄数月，而当前众多的SWCC方程研究仅考虑单一或者是两影响因素的特殊状态，其方程足够复杂；同时，SWCC方程参数对试验数据量及数据分布敏感，即SWCC曲线拟合精度与试验数据量成正相关，而试验数据点越多，则曲线测定越耗时。这些因素成为制约SWCC方程工程应用的重要原因。因而，寻找对试验数据量依赖性低、包容主要土-水影响因素、能够处理多组分复合介质在多应力耦合作用下的广义SWCC方程，成为土-水关系研究的关键。

本文旨在基于van Genuchten土-水方程[11]、Fredlund等[17]的双应力变量理论及Tarantino研究[25]，导出考虑土体变形、应力状态及多孔隙集群分布的广义SWCC方程，为定量表征和拟合土壤土-水关系提供理论参考，为后期土体变形、强度及渗透的水力-力学本构研究提供参考。

1 经典SWCC评价与比较

表1列出部分经典的SWCC模型，并比较其特点和适用范围。

表1 经典土-水特征曲线表征方程及其特点和适用范围

注：在某状态下的整条脱湿或吸湿SWCC曲线上和为定值，表中未将其纳入参数数量统计。

Note:andare constants during drying/wetting process of SWCC at certain condition and thus not included in counting of parameter numbers.

由表1可见，众多SWCC方程都仅考虑1或2个因素，方程曲线对试验数据量及数据分布敏感性高因而试验测定较为耗时。包承纲[30]针对粉质黏土将工程关心的吸力∈[,]（为残余含水量对应的吸力、为进气值，kPa）段认为是半对数坐标上的直线，提出了简单易用的表达式

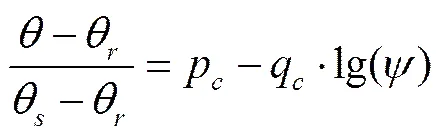
式中p、q为拟合参数；为体积含水量，%；为残余体积含水量，%；为饱和体积含水量，%；为吸力，kPa。

黄海等[31]提出考虑净平均应力影响的SWCC

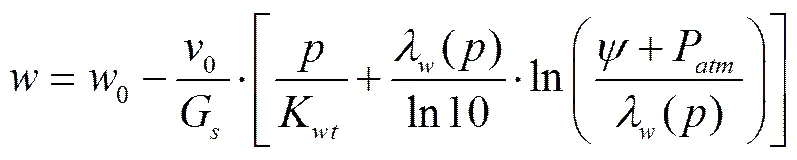
式中0为初始含水率，%；0为初始比容；G为土粒相对密实度；为净平均应力，kPa；K为与净平均应力相关的切线体积模量，kPa；()为常数；P为大气压，kPa。

周葆春等[32]基于Fredlund等的方程提出考虑吸力引起体变的膨胀土SWCC方程，但未涉及附加正应力引起变形的情形，也没有涉及多孔隙集群状态。Tarantino[25]在不考虑残余饱和含水量及多峰的情况下，导出了考虑孔隙比变化的SWCC方程。

鉴于此，笔者认为，SWCC模型具有较好的适用性，至少应具有以下3个特点：1）具有足够的表征精度；2）方程参数对试验数据量依赖性低；3）便于工程应用。

2 双应力变量广义SWCC模型

2.1 广义SWCC图示及概念

通常，SWCC可划分为边界效应区（boundary-effect zone，BE-Z）、过渡区(transition zone，T-Z)、非饱和残余区（residual zone of unsaturation，RU-Z）3个区域[16]，本文称这3个区为“特征吸力域”。对于连续级配或单一级配土壤，其孔隙尺寸密度分布函数（pore-size density probability distribution function, PDF）为一个S形的单峰形态，SWCC也呈单峰形态，如Fredlund等的方程[27]；自然土壤及工程填土等不可能是完全的连续级配，同时存在干湿裂隙，使PDF[33]呈现双峰甚至多峰，SWCC也会对应多个S形态变化[34]，如Rahardjo等[22]的方程。此外，应力（如上覆压力）会引起体变，改变SWCC形态。鉴于此，定义广义土-水特征曲线：基于多因素（如孔隙结构、应力历史、应力状态）影响下土壤吸力与含水量（S、及）之间关系的空间曲线。构建全吸力域（∈[0,106] kPa）双应力变量下体积含水量与吸力关系的广义SWCC概念平面图，如图1所示。

2.2 双应力变量广义SWCC模型

地球表层土壤因处于大气干湿交替、地质营力及人类生产建设活动中，其结构随机、组分多相、应力场耦合，水力-力学性质复杂多样。为便于处理，将应力对土体结构的影响归为：1）应力历史（stress history），如初始固结压力造成的密度、孔隙比的不同的影响，用初始孔隙比0表征；2）应力状态（stress state），即吸力与净法向应力的影响，用孔隙比表征，刻画试验过程应力耦合对土壤结构状态的影响。定义相对体积含水比为

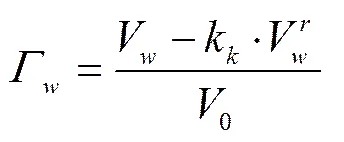
式中为相对体积含水比，无量纲；V为某级吸力平衡时试样含水体积，mL；0为试样初始体积，mL；为广义残余含水体积，mL；当≤时，（为大孔隙及微孔隙粒组SWCC交汇点含水体积，mL），当>时为多峰土-水方程吸力最大段残余含水体积，mL；k为相对比容，k=v/v，其中为比容（1），v为广义残余含水量对应的比容（1+e），e为广义残余含水量对应的孔隙比。

van Genuchten土-水表征方程是最经典的SWCC之一，得到了广泛的理论和试验验证[8-10,13,28,35]，其归一化含水量为[11]

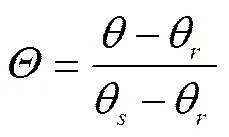
变化规律用形如sigmoidal函数的曲线方程[11]表示为

（5）

式中为与进气值相关的土性参数，kPa-1；为>时土体脱湿速率相关的土性参数，无量纲；为与残余含水量相关的土性参数，无量纲。

可在坐标系∈[,]中进行表征。一般-SWCC、-SWCC、S-SWCC均具有S形变化的规律；还可以表示为以及（为残余饱和度，%；w为残余含水率，%；w为饱和含水率，%）。-SWCC最常用于土壤科学，其本身包含了孔隙变化的因素，因而特别适用于双应力变量的情形，本文采用-SWCC进行推导。-SWCC及S-SWCC可由=·(1+)/G与S=·(1+)/换算得到。式（5）仅考虑吸力单应力状态变量影响，没有考虑及多峰SWCC情形，其应用受到较大的限制。

定义相对变动体积含水量为

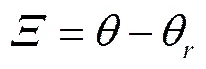
据土壤固-液-气三相关系，由式（3）及式（6）得

（7）

式中0为初始比容。

将式（7）代入式（4）及式（5），得到的另一种表达式

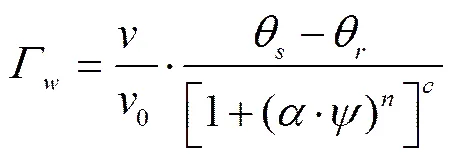
由图1双应力广义SWCC概念图示，结合式（3）、式（6）、式（7）得到图2所示全吸力范围双对数−lg()−lg()平面图，不同特征吸力域划分对应图1。对应的特征吸力域的−lg()−lg()平面曲线最小二乘法拟合表明，−lg()−lg()在相应的特征吸力域内具有很好的线性关系（相关系数>0.90，<0.05）。

注：1~5分别为第1~5段拟合直线的相对体积含水比；1,1,2,2表示相邻2个特征吸力域交界点的吸力，kPa。

Note:1-5are relative volumetric water ratio corresponding to the first to the fifth fitting line segment, respectively;1,1,2and2are matric suction corresponding to jointing point between adjacent suction domains, kPa.

图2 双对数坐标下广义SWCC的相对体积含水比概念图

Fig.2 Concept map of relative volumetric water ratio of generalized SWCC in log-log coordinate

（9）

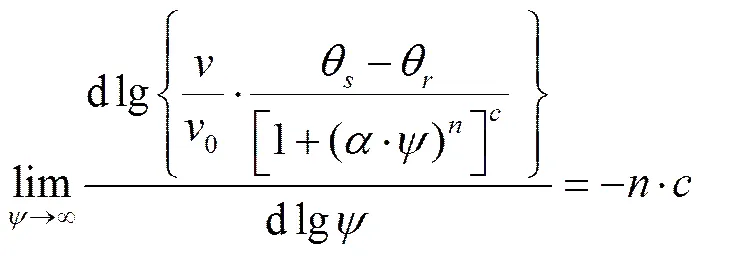
当®∞时，由=10，=−·，及式（8）得

（11）

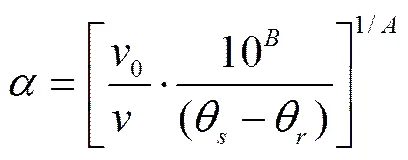
（13）

式（13）为单峰SWCC情形；针对复杂多孔隙尺度集群分布的土体双应力变量条件下的土-水关系的多峰SWCC，可用式（13）对各孔隙尺度集群的SWCC单独表征，即

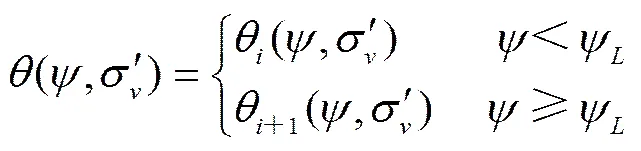
式中角标表示第个SWCC。多峰SWCC还可以表示为多个SWCC的不同权重下的线性叠加，即

（15）

式中表示第个SWCC的权重因子，且0<≤1、。

通常，边界效应区及非饱和残余区内SWCC随吸力的变化并不明显，过渡区SWCC随吸力变化剧烈，三者构成形如S形的变化规律。利用过渡区至少2个土-水数据点代入式（6）和式（7），并结合图2计算得到参数及；利用这2个已知土-水数据点以及参数和，再增加同条单峰SWCC边界效应区至少1个土-水数据点（这个点可以是初始已知土-水数据点），共至少3个土-水数据点，代入式（13）即可绘制出具有适宜精度的整条单峰SWCC。对于多峰SWCC，可采用式（14）分多段SWCC计算得到，也可以采用式（15）不同权重的方式得到。对于全吸力范围SWCC，即具有明显非饱和残余区的SWCC，增加至少1个该区域的数据（其中1个点可以在最大吸力106kPa处含水量为0时获得）应用式（13）拟合，即可得到具有适宜精度的全吸力范围SWCC。这样，使得新SWCC方程对试验数据量的依赖性大为降低，可节省试验时间。

当土体孔隙比随吸力变化很小或是不考虑其变化时，式（13）退化为van Genuchten形式

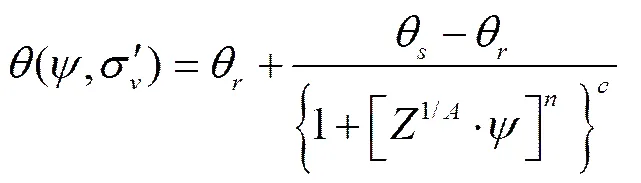
3 双应力广义SWCC预测与评价

为避免拟合的主观性，采用最小二乘法[36]进行拟合。在−lg()−lg()平面，令，，则

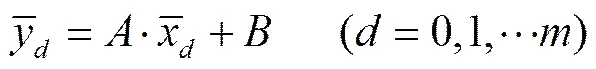
式中角标表示在某特征吸力域内第个吸力平衡时的数据，下同。

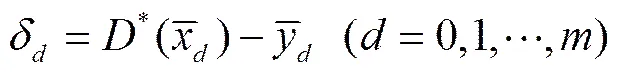
（19）

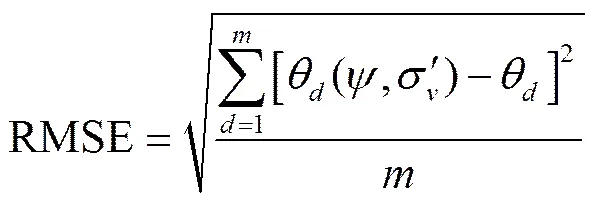
（21）

式中(,)为吸力及相应的净法向应力下的试验体积含水量；为对应应力状态曲线上的预测体积含水量。

随之，一个完整的双应力变量广义SWCC预测-拟合方程求解过程可用图3表示。由图3可见，式（13）广义SWCC方程形似复杂，但应用Matlab、Origin及1stOpt等软件，即可实现自动化、高精度的拟合及预测，操作起来十分简便。由于其函数构造符合SWCC的S形变化规律，其预测及拟合效果将较为理想。

4 讨 论

论文基于Tarantino[25]方程，创新与不同在于：1）Tarantino的土-水表征方程在基于van Genuchten[11]方程推导时，利用饱和度导出土-水表征方程（为相关拟合参数）。形式上，该方程表征的情形是S∈[0,1]，但确切说是有效饱和度∈[0,1]。由于一般土壤都具有明显的残余饱和度或残余含水量，含水量变化区间为S∈[,1]。为此，Tarantino方程拟合容易出现拟合性差、不收敛等问题。应用Tarantino表征式可潜在地将SWCC向下平移个单位，因而其应用会受到限制。以∈[,]（或S∈[,1]）作为其含水量变化区间，能真实地反映SWCC变化规律。Fredlund等[27]的方程能够解决这个拟合不收敛问题，具有较好的灵活性，但试验数据的多少决定着SWCC的形状和走势，且存在不能用于预测土-水关系的缺点。本文定义了“相对体积含水比”，针对非饱和土构建−lg()−lg(w)平面，将普通SWCC方程扩展到考虑多峰效应、应力影响以及体变量测的广义方程。相较于2个参数Brooks等方程[18]、3个参数van Genuchten方程[11]以及4个参数Fredlund等方程[27]，本文的广义SWCC方程仅3个参数，表征了考虑孔隙概率分布函数的影响的双应力变量广义SWCC。参数从−lg()−lg()平面进行线性拟合得到，分别为该平面直线在相应特征吸力域的斜率和截距，广义残余含水量相关参数需要在SWCC方程拟合得到，非常方便。SWCC虽具有较大的工程价值，但其试验动辄数月，每个吸力点平衡需要2～30 d不等，特别是低含水量时需要时日更长，仅1条脱湿SWCC可能就需要数月时间；−lg()−lg()平面吸力域内的曲线具有良好线性关系，由最小二乘法特征可知，参数、的获取并不需要太多的SWCC试验数据，理论上在特征吸力域获取至少3个以上的试验点即可较好地预测该区域SWCC其他点。可利用压力膜法、压力板法[38]、滤纸法[35]、蒸汽平衡法[39]及冷镜露点技术（chilled mirror dew point technique）[40]等对SWCC特征吸力域分段测量，特别是过渡区的量测，可在较短的时间内获得完整SWCC，满足工程需要。

5 结 论

评价了各种经典土-水特征曲线（soil-water characteristic curve, SWCC）表征方程的适用范围及局限，基于Fredlund等的双应力变量理论及van Genuchten土-水方程，定义了广义土-水特征曲线及“相对体积含水比”概念，构建了考虑土体孔隙分布形态及双应力变量影响的广义SWCC方程，结论如下：

1）当前众多SWCC模型不具有包容复杂因素的能力，参数对试验数据量依赖性大，不能同时刻画不同类型土壤不同孔隙结构、双应力状态及土体变形的情况，特别是众多SWCC需要较多试验数据，这是限制其应用的重要原因。

2）应力对SWCC的影响可归纳为应力历史（固结压力、初始孔隙比等）及应力状态（吸力及净法向应力）2种模式，均在本广义SWCC中得到反映。

3）本文导出的广义SWCC方程仅3个参数，能够包容各种孔隙分布情况双应力状态的复杂土-水关系。不仅能够用以拟合SWCC，还能结合SWCC试验，用至少3个试验数据点，应用Matlab、Origin及1stOpt等软件预测更大吸力范围的土-水关系，大大节省试验时间。研究可为土壤的节水灌溉、水土保持、边坡失稳机理以及滑坡灾害的防治提供理论参考；新方程的精确性及实用性将在进一步的试验研究中进行检验。

[1] Salager S, Nuth M, Ferrari A, et al. Investigation into water retention behaviour of deformable soils[J]. Canadian Geotechnical Journal, 2013, 50(2): 200－208.

[2] Keller T, Lamandé M, Peth S, et al. An interdisciplinary approach towards improved understanding of soil deformation during compaction[J]. Soil and Tillage Research, 2013, 128: 61－80.

[3] 程明书，汪时机，张雅倩，等. 膨胀土损伤变量不同表征方法评价的试验研究[J]. 岩土力学，2015，36(10)：2892－2898.

Cheng Mingshu, Wang Shiji, Zhang Yaqian, et al. Experimental study of assessment of different damage variable characterizations of expansive soil based on CT-triaxial tests[J]. Rock and Soil Mechanics, 2015, 36(10): 2892－2898. (in Chinese with English abstract)

[4] 程明书，汪时机，毛新，等. 结构性损伤膨胀土三轴加载下的裂隙形态及力学表征[J]. 岩土工程学报，2016，38(增刊2)：73－78.

Cheng Mingshu, Wang Shiji, Mao Xin, et al. Fissure morphology and corresponding mechanical behavior modeling for virgin structure-damaged expansive soil under triaxial compression tests[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(Supp. 2): 73－78. (in Chinese with English abstract)

[5] 汪时机，陈正汉，李贤，等. 土体孔洞损伤结构演化及其力学特性的CT-三轴试验研究[J]. 农业工程学报，2012，28(7)：150－154.

Wang Shiji, Chen Zhenghan, Li Xian, et al. Pore-damage evolution and mechanical properties of remolded soil by CT-triaxial test[J]. Transactions of the Chinese Society of Agricultural Engineering Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(7): 150－154. (in Chinese with English abstract)

[6] 俞培基，陈愈炯. 非饱和土的水-气形态及其与力学性质的关系[J]. 水利学报，1965(1)：16－24.

Yu Peiji, Chen Yujiong. The pore air-water configurations and their effects on the mechanical properties of partially saturated soils[J]. Journal of Hydraulic Engineering, 1965(1): 16－24.(in Chinese with English abstract)

[7] Chen Rui, Liu Jian, Li Jinhui, et al. An integrated high-capacity tensiometer for measuring water retention curves continuously[J]. Soil Science Society of America Journal, 2015, 79(3): 943－947.

[8] Minasny B, McBratney A B, Bristow K L. Comparison of different approaches to the development of pedotransfer functions for water-retention curves[J]. Geoderma, 1999, 93(3/4): 225－253.

[9] Hardie M A, Lisson S, Doyle R B, et al. Evaluation of rapid approaches for determining the soil water retention function and saturated hydraulic conductivity in a hydrologically complex soil[J]. Soil & Tillage Research, 2013, 130: 99－108.

[10] Hallema D W, Periard Y, Lafond J A, et al. Characterization of water retention curves for a series of cultivated histosols[J]. Vadose Zone Journal, 2015, 14(6): 1－8.

[11] van Genuchten M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44(5): 892－898.

[12] Barlow K, Nash D. Investigating structural stability using the soil water characteristic curve[J]. Australian Journal of Experimental Agriculture, 2002, 42(3): 291－296.

[13] 刘建立，徐绍辉，刘慧，等. 参数模型在壤土类土壤颗粒大小分布中的应用[J]. 土壤学报，2004，41(3)：375－379.

Liu Jianli, Xu Shaohui, Liu Hui, et al. Application of parametric models to description of particle-size distribution in loamy soils[J]. Acta Pedologica Sinica, 2004, 41(3): 375－379. (in Chinese with English abstract)

[14] Lee I M, Sung S G, Cho G C. Effect of stress state on the unsaturated shear strength of a weathered granite[J]. Canadian Geotechnical Journal, 2005, 42(2): 624－631.

[15] Ng C W W, Leung A K, Wong H N, et al. A field study of stress-dependent soil-water characteristic curves and permeability of a saprolitic slope in Hong Kong[J]. Géotechnique, 2011, 61(6): 511－521.

[16] Vanapalli S K, Fredlund D G, Pufahl D E. The influence of soil structure and stress history on the soil-water characteristics of a compacted till[J]. Géotechnique, 1999, 49(2): 143－159.

[17] Fredlund D G, Morgenstern N R. Stress state variables for unsaturated soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1977, 103(5): 447－466.

[18] Brooks R H, Corey A T. Hydraulic Properties of Porous Media: Hydrology Papers[M]. Fort Collins: Colorado State University, 1964.

[19] Alonso E E, Gens A, Josa A. A constitutive model for partially saturated soils[J]. Géotechnique, 1990, 40(3): 405－430.

[20] Gallipoli D, Wheeler S J, Karstunen M. Modelling the variation of degree of saturation in a deformable unsaturated soil[J]. Géotechnique, 2003, 53(53): 105－112.

[21] Ciervo F, Casini F, Papa M N, et al. Some remarks on bimodality effects of the hydraulic properties on shear strength of unsaturated soils[J/OL]. Vadose Zone Journal, 2015, 14(9): 1－12. doi:10.2136/vzj2014.10.0152

[22] Rahardjo H, Satyanaga A, D’Amore G A R, et al. Soil-water characteristic curves of gap-graded soils[J]. Engineering Geology, 2012, 125(1): 102－107.

[23] Mbonimpa M, Aubertin M, Maqsoud A, et al. Predictive model for the water retention curve of deformable clayey soils[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2006, 132(9): 1121－1132.

[24] 孙德安，孙文静，孟德林. 膨胀性非饱和土水力和力学性质的弹塑性模拟[J]. 岩土工程学报，2010，32(10)：1505－1512.

Sun De’an, Sun Wenjing, Meng Delin. Elastoplastic modelling of hydraulic and mechan ical behaviour of unsaturated expansive soils[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(10): 1505－1512. (in Chinese with English abstract)

[25] Tarantino A. A water retention model for deformable soils[J]. Géotechnique, 2009, 59(9): 751－762.

[26] Gardner W R. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table[J]. Soil Science, 1958, 85(4): 228－232.

[27] Fredlund D G, Xing A Q. Equations for the soil-water characteristic curve[J]. Canadian Geotechnical Journal, 1994, 31(6): 1026.

[28] Zhang Limin, Chen Qun. Predicting bimodal soil-water characteristic curves[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(5): 666－670.

[29] Burger C A, Shackelford C D. Evaluating dual porosity of pelletized diatomaceous earth using bimodal soil-water characteristic curve functions[J]. Canadian Geotechnical Journal, 2001,38(1): 53－66.

[30] 包承纲. 非饱和土的性状及膨胀土边坡稳定问题[J]. 岩土工程学报，2004，26(1)：1－15.

Bao Chenggang. Behavior of unsaturated soil and stability of expansive soil slope[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(1): 1－15. (in Chinese with English abstract)

[31] 黄海，陈正汉，李刚. 非饱和土在p-s平面上屈服轨迹及土-水特征曲线的探讨[J]. 岩土力学，2000，21(4)：316－321.

Huang Hai, Chen Zhenghan, Li Gang. A study on yield locus of unsaturated soil on p-s plane and soil-water characteristic curve[J]. Rock and Soil Mechanics, 2000, 21(4): 316－321. (in Chinese with English abstract)

[32] 周葆春，孔令伟. 考虑体积变化的非饱和膨胀土土水特征[J]. 水利学报，2011，42(10)：1152－1160.

Zhou Baochun, Kong Lingwei. Effect of volume changes on soil-water characteristics of unsaturated expansive soil[J]. Journal of Hydraulic Engineering, 2011, 42(10): 1152－1160. (in Chinese with English abstract)

[33] Durner W. Hydraulic conductivity estimation for soils with heterogeneous pore structure[J]. Water Resources Research, 1994, 30(2): 211－223.

[34] Li Xu, Li Jinhui, Zhang Limin. Predicting bimodal soil-water characteristic curves and permeability functions using physically based parameters[J]. Computers and Geotechnics, 2014, 57: 85－96.

[35] Leong E C, He Liangcai, Rahardjo H. Factors affecting the filter paper method for total and matric suction measurements[J]. ASTM Geotechnical Testing Journal, 2002, 25(3): 322－333.

[36] York D. Least-squares fitting of a straight line[J]. Canadian Journal of Physics, 1966, 44(5): 1079－1086.

[37] Wijaya M, Leong E C. Equation for unimodal and bimodal soil-water characteristic curves[J]. Soils and Foundations, 2016, 56(2): 291－300.

[38] Ng C W W, Pang Y W. Influence of stress state on soil-water characteristics and slope stability[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(2): 157－166.

[39] Nam S, Gutierrez M, Diplas P, et al. Comparison of testing techniques and models for establishing the SWCC of riverbank soils[J]. Engineering Geology, 2010, 110(1/2): 1－10.

[40] Bulut R, Leong E C. Indirect measurement of suction[J]. Geotechnical and Geological Engineering, 2008, 26(6): 633－644.

Establishment of generalized soil-water characteristic curve theoretical model considering two stress state variables for unsaturated soils

Wang Shiji1, Cheng Mingshu1,Li Xian1,2, Wang Xiaoqi1, Mao Xin1, Yang Huidi3

(1.400715;2.;3.410082,)

As one of the fundamental soil-water modeling equations, soil water characteristic curve (SWCC) equation is widely employed to study soil-water retention, permeability and strength characteristics in the fields of agricultural engineering, environmental engineering, geotechnical engineering, etc. In this study, we evaluated the current classic SWCC equations and proposed a generalized SWCC model. By summarizing the current models, we found that the current model considered only a single or two influential factors, the forms of the current equations were complex, they were sensitive to experimental data and the fitness accuracy was highly dependent on the numbers of the experimental points. And most of them couldn’t deal with the conditions of multimodal pore-size density probability function and hydro-mechanical coupling effects for the solid-liquid-gas materials in soil. Based on Fredlund et al’s two stress variables theory and van Genuchten’s soil-water characteristic equation, the concept of generalized SWCC was defined. Three characteristic suction zones included boundary-effect zone, transition zone and residual zone of unsaturation. We defined the generalized SWCC as spatial curves reflecting relationship between matric suction and soil water content under the condition affected by multiple factors such as pore structure, stress history and stress state. The relative volumetric water ratio was proposed. The stress history was expressed with initial void ratio and the stress state was described with void ratio. Thus, the relative volumetric water ratio was defined as a ratio of water content-related function and initial volume. Relative fluctuated volumetric water content was defined as the difference of volumetric water content and residual volumetric water content. Based on the relative fluctuated volumetric water content, the relative volumetric water ratio was expressed as the other form. Then, the figure of net normal stress-logarithm of matric suction-logarithm of relative volumetric water ratio corresponding to the characteristic suction zones was plotted. A good linear relationship (>0.90,<0.05) was found among the net normal stress, logarithm of matric suction and logarithm of relative volumetric water ratio. Thus, the generalized two stress state bimodal SWCC model was derived, which considered the multimodal pore-size density probability distribution function and soil deformation. Compared with the 2-parameter Brooks et al’s equation, 3-parameter van Genuchten equation as well as the 4-parameter Fredlund et al’s equation, the proposed generalized SWCC only had 3 parameters, 2 of which could be obtained by least-square linear fitting method in the plane of log-log coordinate system of relative volumetric water ratio versus matric suction and only one of which would be achieved by the nonlinear least-square fitting method. The model fitness needs at least 3 experimental points. The model provides with a new way to predict the soil-water retention, permeability, strength of soil quantitatively in an easier and timesaving process.

soil moisture; stresses; models; water retention property; unsaturated soil; soil-water characteristic curve; bimodal SWCC

10.11975/j.issn.1002-6819.2017.06.001

TU411; S152

A

1002-6819(2017)-06-0001-07

2016-07-04

2016-11-20

国家自然科学基金项目资助（11572262）；中央高校基本科研业务费专项资金资助（XDJK2016D016, XDJK2016B006）

汪时机，男，安徽安庆人，教授，博士，主要从事农业水土工程和岩土力学方面的教学和研究。重庆西南大学工程技术学院，400715。Email：shjwang@swu.edu.cn