一道“网研”几何难题的思路探求与教学思考

☉江苏苏州工业园区星湾学校许莹洁

一道“网研”几何难题的思路探求与教学思考

☉江苏苏州工业园区星湾学校许莹洁

随着网络信息技术的普及，各地试题资源往往能借助于自媒体第一时间在一些QQ群、微信平台上传播，特别是一些设计精巧的较难平面几何题往往能吸引很多同行的研究兴趣，面对复杂的构造，尝试作辅助线但思路受阻的解题心得、柳暗花明贯通思路后的悠然神会，总是较难几何题带给我们的心理体验.本文记录最近在某QQ群里一道几何难题的思路突破，同类链接，并跟进教学思考，供分享.

一、考题及思路突破

考题1：在平面直角坐标系中，点A的坐标为（4，2），点P、Q分别是x轴正半轴、y轴正半轴上的动点，以AP为直径作⊙M，与x轴交于另一点B.

（1）如图1，若OQ=2OP，设线段PQ与线段OA交于点C，求证点C在⊙M上；

（2）若OQ=2OP，连接AQ，当AQ与⊙M相切时，求点P的坐标；

（3）如图2，若OQ=2OP-4，当点P在点B左侧时，连接BQ交⊙M于D，小南同学经过演算，发现BD·BQ的值不会发生变化！请判断小南同学的发现是否正确，并说明理由.思路突破：

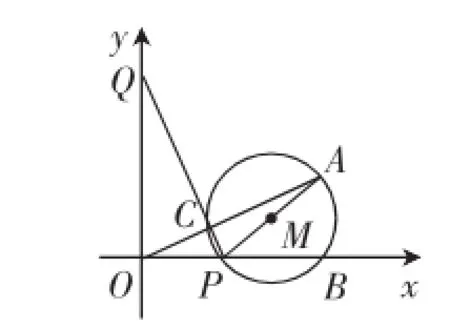
图1

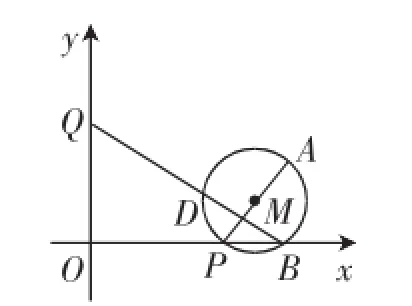
图2

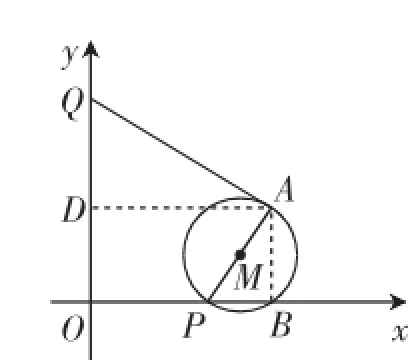
图3

（1）这一小问的关键是证出AO⊥PQ，这样就有∠ACP= 90°，从而90°圆周角所对的弦AP是直径，于是点C在圆M上！有了明确的目标（证AO⊥PQ）之后，就容易想到证△AOB∽△POQ，从而实现问题的突破.

（2）如图3，当QA与⊙M相切时，设P（m，0）、Q（0，2m），作AD⊥y轴于点D，则容易证出△ADQ∽△ABP.于是，代入数据与参数得，从而得出m=.故点P的坐标，0）.

（3）猜想BD·BQ的值不会发生变化，理由如下：

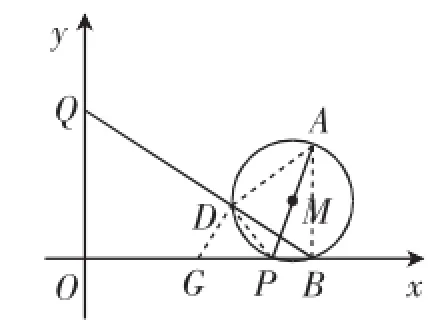
图4

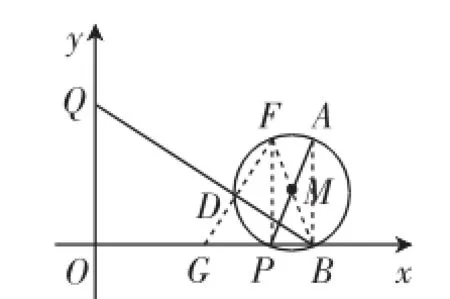
图5

由乘积式的形式，我们可联想到过D点作DG⊥BQ，交BO于G，这样构造出△BDG∽△BOQ，可得比例式=，化为乘积式BD·BQ=BO·BG，显然，要想乘积式BD·BQ为定值，只要BG为定值即可，接下就是重点攻克BG是否为定值.连接AD、AB，可以根据互余的性质，转换出两组锐角相等，即∠BDA=∠PDG，∠ABD=∠PGD，于是△ABD∽△PGD，可得比例式.而前面的△BDG∽△BOQ会带来.可设P（m，0），则Q（0，2m-4）.代入比例式，解出PG=m-2.于是OG=OP-PG=m-（m-2）=2，至此柳暗花明、思路贯通：G为OB的中点！即BD·BQ=2×4= 8.

方法二：由上面方法的分析，解题的关键是求证G为OB的中点.向着这一目标，我们还可构造直径BF（延长BM交圆于F），再连接FD交OB于G点，连接FP.我们可以得出PF=AB=2，∠GDB=∠FDB=90°，可以证出△FPG∽△BOQ，可得比例式所以PG=OQ.设 P（m，0），则Q（0，2m-4），PG=m-2.于是OG=OP-PG=m-（m-2）=2.再由△BDG∽△BOQ，可得比例式则BD·BQ=BO·BG=2×4=8.问题获解.

二、解后反思、易错分析与同类链接

易错分析：这道较难几何题主要难在第（3）问的思路突破.不但前两问不能启发思路，反而前两问的求解会干扰思路.比如，笔者最初就是思考将第（3）问转向上一问的模式进行求解，考虑到OQ=2OP-4，由于4与OB的长相等，故在Q点上方4个单位取点E，恰好此时OE= 2OP，从而构造出图6进行分析，但是思路受阻.还有一个易错点是：在图6中，连接OA，容易误认为A、O、D三点共线，也会造成思考走偏方向，导出矛盾.

图6

从后来成功求解的图4、图5来看，过点D作DG⊥BQ是十分重要的，因为如此一来目标就可明确为证G为OB的中点，从而实现问题突破.

同类链接：在思考上面考题的思路时，笔者曾网络检索，有一些同类题，最早的貌似出自以下一道考题，这里不妨链接如下，供有兴趣的同行对比、研习.

考题2：（2002年湖北武汉中考题）如图7，在直角坐标系中.点E从O点出发，以1个单位/秒的速度沿x轴正方向运动，点F从O点出发，以2个单位/秒的速度沿y轴正方向运动.B（4，2），以BE为直径作⊙O1.

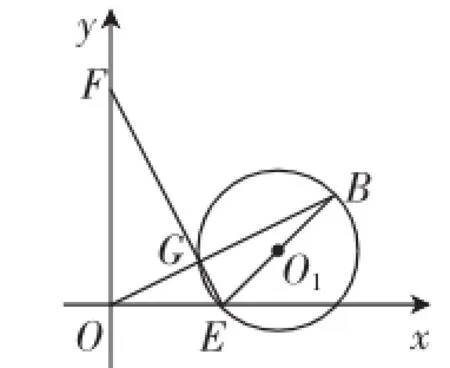
图7

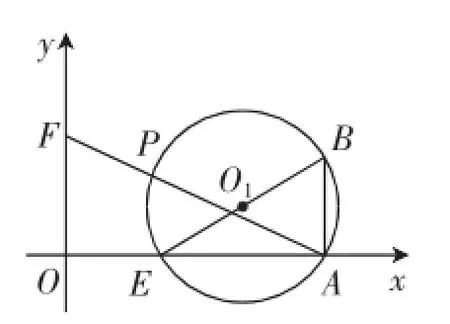
图8

（1）若点E、F同时出发，设线段EF与线段OB交于点G，试判断点G与⊙O1的位置关系，并证明你的结论.

（2）在（1）的条件下，连接FB，几秒时FB与⊙O1相切？

（3）如图8，若点E提前2秒出发，点F再出发，当点F出发后，点E在A点的左侧时，设BA⊥x轴于点A，连接AF交⊙O1于点P，试问：AP·AF的值是否会发生变化？若不变，请说明理由并求其值；若变化，请求其值的变化范围.

说明：限于篇幅，这里不再给出这道考题的解析，思路完全同考题1.

三、教学预设与变式再练

以下我们主要围绕该题第（3）问在解题教学时如何突破解题难点设计一些教学环节.

先让我们把第（3）问重新表述如下：

考题3：如图2，在平面直角坐标系中，点A的坐标为（4，2），点P、Q分别是x轴正半轴、y轴正半轴上的动点，且OQ=2OP-4.以AP为直径作⊙M，与x轴交于另一点B.当点P在点B左侧时，连接BQ交⊙M于D，求证BD·BQ的值不会发生变化.

辅助问题1：过点D作DG⊥BQ交x轴于G，求证：△BDG∽△BOQ.

辅助问题2：连接AD、AB、PD，求证：△PDG∽△ADB.

辅助问题3：求证

辅助问题4：设P（m，0），用含m的式子表示点Q的坐标.

辅助问题5：求证G是OB的中点；

辅助问题6：BD·BQ的值可以转化为哪两条线段之积？

设计说明：上述6个辅助问题其实就是解题的系列步骤，辅助问题就是问题铺垫，学生拾级而上，就可获得问题最终的突破.

在讲评之后，还可跟进如下的变式改编、巩固再练.

变式再练：在平面直角坐标系中，点A的坐标为（6，3），点M、N分别是x轴正半轴、y轴正半轴上的动点，以AM为直径作⊙P，与x轴交于另一点B.

（1）如图9，若ON=2OM，设线段MN与线段OA交于点C，求证点C在⊙P上；

（2）若ON=2OM，连接AN，当AN与⊙P相切时，求点N的坐标；

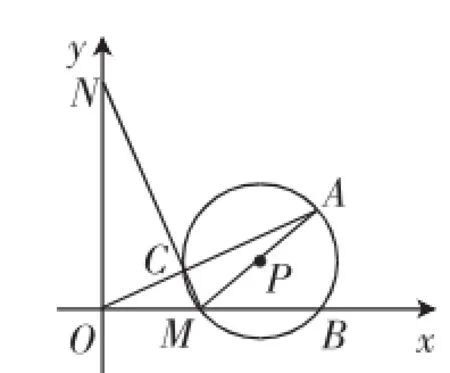
图9

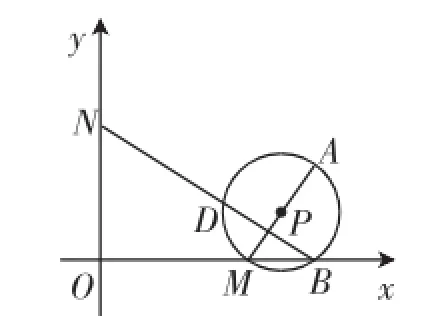
图10

（3）如图10，若ON=2OM-4，当点M在点B左侧时，连接BN交⊙P于D.

①连接AD、DM，作DH⊥BN，交OB于H点，求点H的坐标；

②求证BD·BN是一个定值.

四、两点思考

1.难题求解重在思路突破，回到基本概念去寻找自然的解法.

难题之难常常在于读不懂题意，或由于某些信息的干扰，导致解题方向走偏，耗时费力.上面在考题1解后的易错分析中已指出笔者探求思路过程中一些“白劳”.而从最后成功求解的经验来看，回到基本概念，构造相似三角形是成功突破的关键.这也启发我们解题时要善于回到基本概念去寻找自然而然的解题念头，而不是钻在一个模式之中跳不出思维定式.特别是像考题1这样的前两问与第三问并没有多大关联的试题，往往容易干扰我们的有效思考，值得警惕.当然，这里也需要从命题角度展开思辨，对于惜时如金的考场试题，如果把几个无甚关联的小问拼凑在一起，看似有形式上的联系，但解题思路却无甚联系，这种题建议慎用.

2.命题检测慎用平面几何难题，平时教学时可通过辅助问题分解难点.

根据我们的命题研究、解题经历，在各级重大考试中，一旦出现一道较难的平面几何题，则常常是学生失分的“重灾区”，究其原因，并不一定是学生几何能力下降，而是很多较难的平面几何题往往都需要复杂的、技巧较高的构造、转化，这对于限时答题、大容量试卷来说，显然学生没有足够的时间来深入思考，故命题检测时建议慎用较难几何题.现在想来，国家课程标准一再降低平面几何的教学要求，也是有道理的，值得每一个命题者思考.这里也不得不评说目前个别地区的命题风格，过分倾向于繁杂几何题的考查，有些中考几何题需要构造3条辅助线才能顺利解决，有的几何题需要技巧极高的相似构造，并且需要连续使用2~3次相似三角形（像上面考题1的第（3）问）才能贯通思路.而这些超高要求，在国家课程标准中都是不作考试要求的.当然，在平时教学中，我们也可倾听著名特级教师李庾南老师所指出的“下要保底，上不封顶”的教学要求，即可以利用数学习题课、活动课或课外安排优秀学生深入探究一些有挑战的几何难题.在开展较难几何题讲评时，我们在上面设置辅助问题的做法，对引导学生自主理解难题有较好的效果.

1.何明.由博返约，追求简洁——一道“双曲线”综合题的命题过程［J］.中学数学（下），2015（11）.

2.朱金祥，刘东升.数学教学中例题变式的策略——基于教学追问的视角［J］.教育研究与评论（中学教育教学版），2016（09）.

3.付小飞.明辨并列与递进，引导分离和聚焦——2016年江苏苏州中考第28题解析与教学思考［J］.中学数学（下），2016（7）.

4.章建跃.“题型+技巧”的危害［J］.中小学数学（高中版），2010（11）.