汽车稳定控制系统执行器与传感器故障诊断与估计
王德军,鲍亚新,张贤达
(吉林大学通信工程学院,吉林 长春 130012)
汽车稳定控制系统执行器与传感器故障诊断与估计
王德军,鲍亚新,张贤达
(吉林大学通信工程学院,吉林 长春 130012)
汽车稳定控制系统具有明显的非线性特性,对其传感器与执行器的故障诊断具有一定难度。从汽车八自由度模型入手,简化模型并建立虚拟输入。针对虚拟输入模型,将虚拟执行器故障作为增广状态向量的一部分,构造一个增广系统。利用李雅普诺夫理论设计观测器,获得原系统状态与虚拟执行器故障的渐近估计,并分析了增广观测器的稳定性与收敛性。通过LMI技术实现线性矩阵不等式求解,完成观测器设计。选择一个新的状态变量作为输出信号滤波器,将传感器故障转化为执行器故障,建立二增广系统,直接利用执行器故障诊断方法实现传感器故障诊断。通过Simulink,验证了此方法的可行性。与其他方法相比,该方法不仅能够同时得到虚拟执行器与传感器故障信号,为系统提供警示,而且为后续的容错控制设计提供可靠数据。
汽车; 执行器; 传感器; 故障诊断; 非线性; 容错控制
0 引言
近年来,随着行驶路况日益复杂,汽车电子稳定控制系统(electronic stability control,ESC)已成为汽车标配[1]。ESC系统中的传感器与执行器故障能否被快速诊断,并实现相应的故障容错,是车辆稳定性控制的关键问题。故障诊断方法有很多[2],针对车辆稳定控制系统故障诊断,Kiencke 等[3]采用龙伯格观测器方法的反馈增益设计;Edwards采用滑模观测器(slide mode observer,SMO)方法[4];宋应采用观测器方法[5],对汽车侧倾角速度故障进行了诊断和重构。但这些方法主要是对车辆稳定系统进行局部故障诊断,不能全局把握车辆行驶中故障信息,给容错控制设计带来了很大不便。为此,本文针对ESC系统,设计了联合故障估计与诊断观测器。
1 汽车模型的建立
1.1 汽车八自由度模型
车辆动力学模型可简化为八自由度车辆模型,即x轴方向上的纵向运动、y轴方向上的侧向运动、绕x轴的侧倾运动、绕z轴的横摆运动及四个车轮的转动[6]。八自由度车辆模型如图1所示。

图1 八自由度车辆模型
汽车的运动方程和动力学方程分别为:
(1)
(2)
(3)
(4)
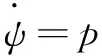
(5)
式中:m为汽车总质量;ms为汽车簧载质量;vx为纵向车速;vy为横向车速;ω为横摆角速度;ψ为侧倾角;p为侧倾角速度;e为簧载质量的质心到侧倾中心的距离;Iz为整车绕车辆坐标系z轴的转动惯量;Ixz为整车绕车辆坐标系x轴、z轴的惯性积;Ixs为簧载质量绕车辆坐标系x轴的转动惯量;Ixzs为簧载质量绕车辆坐标系x轴、z轴的转动惯量。
在式(1)~式(5)的基础上,将(vx,vy,ωr,p,ψ)作为车辆运动过程中的状态变量,进行如下整理:
(6)
其中,侧倾方向上的合力矩为:
∑Mx=msgeψ-Kψψ-Gψp=(msge-Kψ)ψ-Cψp
式中:Cψ为侧倾角阻尼;Kψ为侧倾角刚度。
令Δ9=msge-Kψ、Δ10=-Cψ,可得:
∑Mx=Δ9ψ+Δ10p
(7)
1.2 汽车状态方程
令u1=∑Fx、u2=∑Fy、u3=∑Mz,可得到如下所示的状态方程:

(8)
状态方程中的非线性部分为:
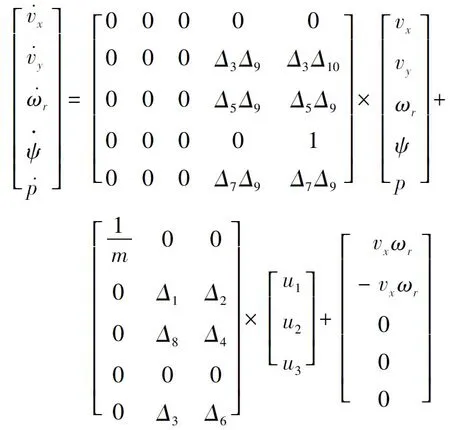
(9)
1.3 执行器和传感器故障建模
1.3.1 执行器故障建模
汽车状态方程满足以下形式:
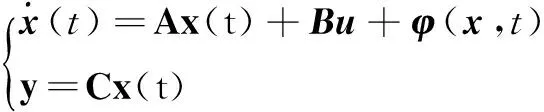
(10)
式中:A、B、C为已知矩阵;φ(x,t)为非线性部分。
假设φ(x,t)相对于x满足李普希兹条件:
‖φ(x1,t)-φ(x2,t)‖≤γ‖x1-x2‖
(11)
式中:‖·‖表示欧氏范数;γ≥0为李普希兹常数。
将执行器故障附加在状态方程(10)中,则:
(12)
式中:Ea为已知矩阵;fa为执行器故障。

(13)
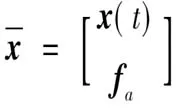
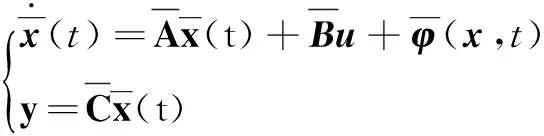
(14)
1.3.2 传感器故障建模
将传感器故障附加在状态方程(10)中,得:
(15)
式中:Es为已知单位矩阵;fs为传感器故障。
定义一个如下的新的状态变量Z,作为输出信号的一阶低通滤波器:
(16)
式中:Z为滤波器状态向量;As、Bs为待设计的滤波矩阵,As矩阵可任意,Bs为满秩矩阵[7]。在此选取As为零矩阵,Bs为单位矩阵。
(17)
由式(15)和式(17),可得:
(18)
则式(18)可变换为:
(19)

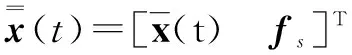

(21)
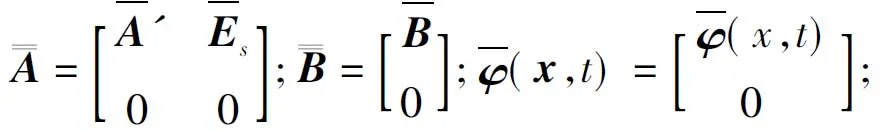

2 观测器设计
2.1 增广观测器
针对状态方程式(14),建立如下形式观测器:
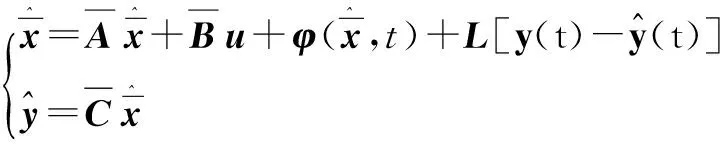
(22)
式中:L为待设计的观测器增益矩阵。

引理1 设x,y是具有相同维数的实数向量,则对于任意整数ε>0,有下面的不等式成立:
2xTy≤εxTx+ε-1yTy
(23)
引理2 设对称矩阵Z为:
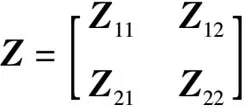
(24)
则Z>0的充分必要条件为:
(25)
利用以下定理设计观测器[10]。
定理1 对于给定得标量λ>0,如果存在对称正定矩阵P∈R(n+q)×(n+q),对称正定矩阵Q∈R(n+q)×(n+q)和矩阵W∈R(n+q)×m,满足如下线性矩阵不等式:

(26)
(27)
式中:λmax(Q)为矩阵Q的最大特征值;λmin(P)为矩阵P的最小特征值。
根据系统模型(14)和观测器(22),可得如下误差动态方程:

(28)

取李雅普诺夫备选函数:
V=eTPe
(29)
式中:P为对称正定矩阵,即P=PT>0。
求导,得:
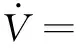
(30)
由引理1,得:
2eTPΔφ≤(Δφ)TΔφ+eTPPe
(31)
根据李普希兹条件(11),可得:
2eTPΔφ≤γ2eTe+eTPPe
(32)

(33)

(34)
(35)
进一步利用引理2,可以将式(34)写成:
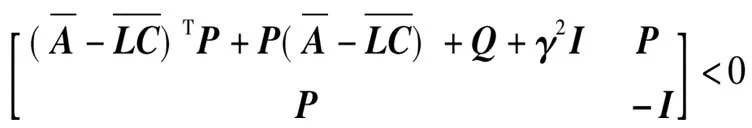
(36)
令W=PL,可得式(26)等价于式(36)。
2.2 增广观测器收敛性
李雅普诺夫函数满足:
V=eTPe≥λmin(P)‖e‖2
(37)
根据式(34),有:

(38)
由式(37)和式(38),可得:
(39)
V (40) 根据式(37)和式(40),可得: (41) 在设计观测器时,可以选择P和Q相关,例如Q=∂P,这样可以保障得到增广观测器的收敛速度。 2.3 二增广观测器 针对二增广系统(21),考虑如下形式观测器: (42) (43) 证明过程与定理1相同,此处省略。 3.1 执行器故障诊断与估计 整车参数如下:M=1 359.8;IZ=1 992.54;MS=1 279.0;e=0.39;IXS=276.871;IXZ=0;Kf=23 540.0;g=9.8;Kr=23 101.0;Cf=2 810.0;Cr=2 810.0。 矩阵A、C为已知矩阵,其中φ(x,t)满足李普希兹条件。此外,Q=P,通过LMI求解矩阵不等式(26),可得执行器增广观测器增益矩阵L,实现观测器设计。 假设故障发生的时间是5 s,故障类型分别为突变故障和恒增益故障,故障形式如下: 图2为纵向合力发生突变故障时,增广状态真实值与估计值对比。由图2可以看出,本文方法很好地估计了汽车状态,如纵向速度,只有在故障发生时有短暂的偏差,并且估计出纵向合力突变故障,而其余执行器故障值为0。 图2 增广状态真实值与估计值对比图 图3为纵向合力发生恒增益故障时,纵向合力故障真实值与估计值对比。由图3可以看出,虽然不能达到对纵向合力故障的准确估计,但故障发生时,观测器故障估计值明显偏向0,达到了故障诊断的目的。 图3 纵向合力恒增益故障真实值与估计值对比图 3.2 传感器故障诊断与估计 通过LMI求解不等式(43),实现了二增广观测器的设计。 假设当t=5 s时,横摆角速度传感器与侧倾角速度传感器同时发生故障,故障形式如下: 图4为传感器故障真实值与估计值对比。由图4可以看出,观测器可以诊断横摆角速度传感器故障与侧倾角速度传感器故障。 图4 传感器故障真实值与估计值对比图 针对汽车八自由度模型,提出了虚拟执行器的概念,并利用增广观测器诊断执行器及传感器故障。该方法操作简单、诊断准确,无论传感器与执行器的故障形式如何,观测器都可以得到准确的诊断结果。虚拟执行器的估计简化了汽车稳定控制系统的容错控制设计,在工程实践中意义深远。 [1] XU L,TSENG H E.Robust model-based fault detection for a roll stability control system[J].IEEE Transactions on Control Systems Technology,2007,15(3):519-528. [2] 范会来,闫英敏,杨凤彪.扩展故障树的非线性链表化故障诊断研究[J].自动化仪表,2013,34(5):16-19. [3] KIENCKE U,DAIB A.Observation of lateral vehicle dynamics[J].Control Engineering Practice,1997,5(8):1145-1150. [4] EDWARDS C,HEBDEN R G,SPURGEON S K.Sliding mode observers for vehicle mode detection[J].Vehicle System Dynamics,2005,43(11):823-843. [5] 王德军,宋石尧,王晰聪.汽车侧倾角速度传感器的故障诊断与重构[J].吉林大学学报(信息科学版),2015,33(2):143-152.[6] PACEJKA H B.Tyre and vehicle dynamics[M].Oxford:Butterworth-Heinemann,2005. [7] CHEE P T,CHRISTOPHER E.Sliding mode observers for reconstruction of simultaneous actuator and sensor fault[C]//Proceedings of the 42nd IEEE Conference on Dicision and Control,USA,2003:1455-1460. [8] CHEN F,ZHANG W.LMI rriteria for robust chaos synchronization of a class of chaotic systems[J].Nonlinear Analysis,2007,67(12):3384-3393. [9] 梅生伟,申铁龙,刘康志.现代鲁棒控制与应用[M].2版.北京:清华大学出版社,2008:84-104. [10]王振华,沈毅,张筱磊.基于增广观测器的非线性系统执行器故障[J].宇航学报,2012,3(12):1742-1746. Fault Diagnosis and Estimation of Actuator and Sensor for Vehicle Stability Control System WANG Dejun,BAO Yaxin,ZHANG Xianda (College of Communication Engineering,Jilin University,Changchun 130012,China) Vehicle stability control system features obvious nonlinear characteristics.It is difficult for fault diagnosis of its sensor and actuator.The eight degree of freedom model of vehicle is simplified and the virtual input is established.Aiming at the virtual input model,the actuator fault is considered as part of augmented state vector,and an augmented system is constructed.The observer is designed by using Lyapunov theory;the asymptotic estimation of the state of original system and the virtual actuator fault is obtained,and the stability and convergence of the augmented observer is analyzed.Through LMI technology,the solution of inequalities of linear matrix is realized,the design of observer is completed.By adopting simple filter,a new state vector is selected as low -pass 1st order filter;the sensor fault is transformed into actuator fault;the 2nd augmented system is constructed,then the fault estimation of sensor is implemented by directly using actuator fault estimation.The feasibility of this method is verified by Simulink.Comparing with other methods,this method can obtain the fault signals of virtual actuator and sensor simultaneously for warning the system,and provide reliable data for subsequent design of fault tolerant control. Vehicle; Actuator; Sensor; Fault diagnosis; Nonlinear; Fault tolerant control 国家自然科学基金重点资助项目(61520106008) 王德军(1970—),男,博士,副教授,主要从事故障诊断和容错控制方向的研究。E-mail:djwang@jlu.edu.cn。 TH-39;TP273 A 10.16086/j.cnki.issn1000-0380.201704010 修改稿收到日期:2016-11-21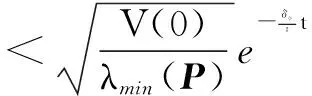
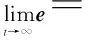



3 仿真验证



4 结束语

