Narendra自适应控制器在球杆系统的应用与研究

高 成,郝洋洋

(沈阳工业大学化工过程自动化学院,辽宁 辽阳 111003)

Narendra自适应控制器在球杆系统的应用与研究

高 成,郝洋洋

(沈阳工业大学化工过程自动化学院,辽宁 辽阳 111003)

作为经典的试验设备之一，球杆系统具有开环不稳定和非线性这两大特性，是控制理论研究的典型对象，是自动控制试验室常用装置，是试验人员实践控制理论基础的平台，也是验证设计人员的新想法、新思路的典型设备。建立了球杆系统及其数学模型，对某些环节进行了线性化处理，得到整个球杆系统的简化模型，作为被控对象的传递函数。基于球杆系统传递函数的特点，设计了一种Narendra自适应控制器，并在Matlab中的Simulink环境下进行实时控制，以验证控制器的控制效果。仿真和试验结果都表明，与PID控制、根轨迹控制相比，自适应控制具有更好的控制效果。自适应控制理论为解决复杂系统控制问题开辟了新的途径，已成为控制领域的研究和发展热点。

控制理论； 自适应控制器； 滤波器； 伺服电机； 电机传动

0 引言

在控制理论的研究中，球杆系统是最为著名的试验设备之一，许多专家、学者都通过球杆系统对其研究的理论进行验证。因球杆系统是一个经典的非线性、单输入单输出、开环不稳定系统，且小球在导轨上的运动十分复杂，故球杆系统得到了广泛的应用。

球杆系统的基本控制思路是：通过控制直流伺服电动机的正反转，带动传动机构调节横杆的倾斜角度，实现对小球运动的控制，进而达到预期位置[1]。本文采用牛顿-欧拉公式建立球杆系统的数学模型,并根据该数学模型选择合适的控制器。

1 系统建模

球杆系统是典型的非线性系统，其运动机构具有许多非线性特点，包括：饱和、死区特性，直流伺服电动机、带轮和连动杆传动的非线性，小球运动轨迹的非线性，小球运动过程中受到空气及非绝对光滑的导轨产生的非线性阻力。 因此，对小球在导轨表面运动动态过程的完整描述是十分复杂的，建模的目的是对该控制系统给出一个较为简单的模型[2-3]。球杆系统机械结构如图1所示。

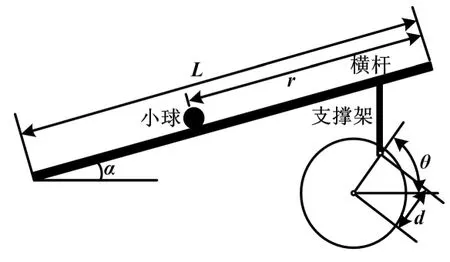
图1 球杆系统机械结构示意图

电机带动带轮转动，连接线(皮带轮中心到支撑架与皮带轮连接点的连接线)和水平线的夹角角度为θ(θ有相应的限定范围)；连杆随之带动横杆转动，角度为α；横杆转动过程中，小球因重力作用开始在横杆内滚动[4]。

皮带轮中心到支撑架与皮带轮连接点的距离为d，横杆的长度值为L，由此可得出倾斜角α与θ之间的近似数学关系式为：

(1)

式中：d为齿轮半径，d=45 mm；L为支撑杆横杆连接点的长度,L=400 mm[5]。

电动机传动轴和θ之间存在一个同步带(减速比n=4)，控制器的设计目的是通过整定θ，保证小球在特定位置保持平衡。

通过运动学对小球的运动情况进行分析，其惯量、重力、转角、位移之间的关系为[6-7]：

(2)

假设小球在横杆上的运动为滚动，且摩擦力可以忽略不计，α很小，则：

sinα=α

(3)

(4)

将式(2)～式(4)化简,得：

(5)

将式(1)代入式(5)，可得：

式中：r为系统输出量，是小球在平衡杆上的位置；θ为输入量，是转盘的转角。

当以θ为系统输入量时，r和θ的传递函数为：

2 Narendra自适应控制器的设计

被控对象的状态、输出方程分别为：

(6)

yp=hTxp

(7)

式中：Ap、bp为未知量；xp为n维状态向量；yp为输出量；u为控制量；h为n×1维向量。

因此，被控系统的传递函数为：

Gp(s)=hT(sI-Ap)-1bp=kpNp(s)/Dp(s)

(8)

式中：kp为被控对象增益。

选取参考模型为：

xm=Amxm+bmyr

(9)

ym=hTxm

(10)

式中：yr为输入信号；ym为输出信号。

参考模型传递函数为：

Gm(s)=hT(sI-Am)-1bm=kmNm(s)/Dm(s)

(11)

式中：km为参考模型增益。

设广义输出误差函数为：

e(t)=ym(t)-yp(t)

根据李雅普诺夫稳定性理论[8]设计自适应控制律(不含误差倒数)，使广义输出误差函数满足以下条件：

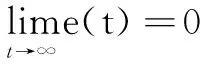
(12)

当式(12)成立时，控制系统具备良好的跟踪性能，达到了设计要求。

当自适应控制器中的可调参数足够多时，可以实现参考模型与可调系统的完全匹配。当控制对象传递函数中的分子为m阶、分母为n阶、被控对象增益为kp时，可调参数数量可多达(n+m+1)个，因此与之对应的自适应机构也应为(n+m+1)个。

因此，自适应控制器可设计如下。

①选择L(s)=s+a(a>0)，使得L(s)G(s)为严格正实函数。

②选择Df(s)=L(s)Nm(s)，并构造辅助信号状态方程:

③可调参数自适应律为：

(13)

(14)

式中：θT=[k0c d0d]；φT=[yrv1ypv2]；e(t)=ym(t)-yp(t)；Γ为正定对称矩阵。

④设计非线性自适应控制律为：

u(t)=θT(t)φ(t)+e(t)ζT(t)Γζ(t)

3 Narendra自适应控制器的实现

通过分析Narendra模型参考自适应控制理论，依据参考模型传递函数，并选用稳定多项式L(s)=s+a，可证明函数L(s)Gm(s)为严格正实函数。

定义增广状态向量为:

(15)

由式(15)可知：ζ1=yr/(s+a)；ζ2=v1/(s+a)；ζ3=yp/(s+a)；ζ4=v2/(s+a)。

为使得被控系统的输出信号与参考模型一致，设计可调参数向量θ为：

θT=[k0cd0d]

选择信号滤波器：

Df(s)=L(s)Nm(s)=(s+a)×(s+1)

(16)

由式(16)获得滤波信号：

v1=u/(s+a)

v2=yp/(s+a)

选择自适应控制律：

(17)

由式(17)可得：

根据式(17)和式(15)，得到控制律为[9]：

4 仿真设计

被控对象的数学模型为：

Gp(s)=1.853/s2

(18)

根据被控对象选择的参考模型为：

(19)

构建的Narendra模型参考自适应控制系统模型如图2所示。在图2中，输入系统的数学模型、参考模型，并进行仿真操作。

图2 Narendra自适应控制系统模型示意图

①在阶跃信号的作用下，PID控制的动态响应曲线如图3所示。根据图3分析可知，PID存在较大的超调量，调节时间较长，并且在一段时间之后出现震动，系统趋于稳定，控制性能良好。

②在阶跃信号作用下，根轨迹控制的动态响应曲线如图4所示。根据图4分析可知，根轨迹控制存在较大的超调量，调节时间较长，稳定后存在稳态误差，控制性能一般。

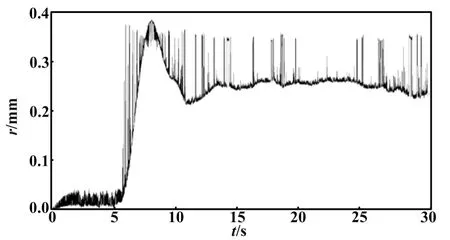
图4 根轨迹控制的动态响应曲线

③在阶跃信号作用下，自适应控制的动态响应曲线如图5所示。根据图5分析可知，自适应控制具有非常好的控制性能。根据参考模型的变化，控制器可以较快地跟随参考模型进行变化。其超调量较小，调节时间较短，控制效果优于PID控制和根轨迹控制。

图5 自适应控制的动态响应曲线

5 结束语

对自适应控制方法在球杆系统上的应用进行研究，建立球杆系统的数学模型，选择Narendra控制器。在Simulink中，选择多种控制算法,包括PID控制[10-11]、根轨迹控制和自适应控制[12-13]，对球杆系统进行实时控制。由实时控制的结果分析可知，在采用了Narendra自适应控制器后，球杆系统达到了较好的控制效果。在输入信号变化的过程中，控制系统都可以保持良好的跟踪性能。

[1] 彭秀艳,宫彬.球杆系统的控制方法研究[J].应用科技,2009,32(12):37-40.

[2] 刘阳,万隆君,徐轶群.浅谈球杆系统的建模与仿真[J].中国科技信息,2014 (6);159-161.

[3] 吴偏偏,王富东,王敬驰.球杆控制系统的设计[J].行业应用与交流,2015,34(9):114-116.

[4] 宋志伟,翟文鹏,信建峰,等.基于PID算法的球杆教学系统设计[J].硅谷,2015 (3):5-6.

[5] 李志民,柳强,张新权,等.基于最小二乘法的球杆系统输入输出建模研究[J].研究与开发,2016,35(1):65-69.

[6] 郑艳伟,张井岗.球杆系统的滑模变结构控制[J].太原科技大学学报,2014,35(2):97-101.

[7] 楼旭阳.基于球杆系统的现代控制理论课堂教学实例设计[J].高教学刊,2016 (8):78-80.

[8] 白珍龙,刘川来.应用Lyapunov理论设计分数阶模型参考自适应控制律[J].石油化工自动化,2015,51(5):44-47.

[9] 庞中华,崔红.系统辨识与自适应控制MATLAB仿真[M].北京:北京航空航天大学出版社,2009:82-83,87.

[10]俞同云.基于闭环特征参数的球杆系统自适应PID控制策略[D].长沙:中南大学,2013.

[11]KRISHNA B,GANGOPADHYAY S,GEORGE J.Design and simulation of gain scheduling PID controller for ball and beam system[D].Signal Processing and Electronics Engineering,2012:199-203.

[12]李宁,袁惠群,孙海义,等.Adaptive control of bifurcation and chaos in a time-delayed system[J].Chinese Physics B,2013,22(3)：030508.

[13]刘幸,刘潇.自适应控制系统的发展与应用[J].学术研究,2011:61-63.

Research on the Application of Narendra Adaptive Controller in Ball-Beam System

GAO Cheng,HAO Yangyang

(College of Chemical Process Automation，Shenyang University of Technology,Liaoyang 111003,China)

As one of the classic experimental equipment,the ball-beam system features open loop instability and nonlinearity,and it is a typical object in research of control theory.It is the commonly used device in automatic control laboratory,and the platform for testers practicing theoretical basis,also it is the typical device for designers verifying their new concept and new ideas.The ball-beam system and its mathematic model are established,and some of the sections are processed for linearity,thus the simplified model of the whole ball-beam system is obtained,and used as the transform function of the controlled object.In accordance with the features of the transfer function of ball-beam system,the Narendra adaptive controller is designed,and the control effects of the controller are verified by conducting real time control in Matlab/Simulink environment.The results of simulation and tests all indicate that,comparing with PID control and root locus control,the adaptive control has excellent control effects.The generation of the adaptive control theory has opened up a new way for solving the problem of complex system control,and become the hotspot in the fields of research and development.

Control theory; Adaptive controller; Filter; Servo motor; Motor drive

辽宁省自然科学基金资助项目(2015020103)

高成(1970—)，男，博士，副教授,主要从事智能控制、机器人方向的研究。E-mail:gc_7011@163.com。

TH7;TP273+.2

A

10.16086/j.cnki.issn1000-0380.201704005

修改稿收到日期：2017-01-17