基于RBF-ARX模型四旋翼飞行器的LQR控制方法*

刘丽丽 左继红 吴 军

(1.中南大学信息科学与工程学院 长沙 410083)(2.湖南铁道职业技术学院 株洲 412001)(3.长沙理工大学电气与信息工程学院 长沙 410083)

基于RBF-ARX模型四旋翼飞行器的LQR控制方法*

刘丽丽1,2左继红1,2吴 军1,3

(1.中南大学信息科学与工程学院 长沙 410083)(2.湖南铁道职业技术学院 株洲 412001)(3.长沙理工大学电气与信息工程学院 长沙 410083)

针对四旋翼欠驱动系统飞行过程中具有的非线性和强耦合性,提出了基于RBF-ARX模型四旋翼飞行器的LQR控制器设计方法。该法首先根据四旋翼飞行器的动力学特性构建四旋翼飞行器RBF-ARX的模型结构,并采用离线非线性参数优化方法辨识模型参数,获取满足工程精度需要的四旋翼非线性动态模型。然后,基于该模型设计了具有状态反馈的四旋翼飞行器的LQR控制器,并通过求解工作点的Riccati方程,获得状态反馈矩阵。最后通过仿真和实时控制结果验证了该方法的有效性和可行性。

四旋翼飞行器; 非线性; 姿态控制; 状态反馈; 实时控制

1 引言

四旋翼飞行器的起飞和巡航是由四个螺旋桨配合完成的,通过改变各旋翼转速,就能控制飞行姿态,具有结构简单、操纵方便以及灵活机动等优点,通常被设计成无人驾驶的微型飞行器。广泛用于野外航拍或飞行侦查等军事领域,也用于建筑物内的导航与勘测等商业和民用领域。

实际应用中,四旋翼飞行器是一个多输入多输出的复杂非线性系统。目前绝大多数的研究,主要集中在非线性控制器的设计方面。文献[1]采用PID控制策略和LQ控制策略实现四旋翼飞行器的控制[1]。文献[2]提出了具有指数收敛特性的PD2反馈结构来补偿飞行过程中的螺旋力矩[2]。文献[3]提出了一种将鲁棒非线性PI控制策略和backstepping技术相结合的方法[3],实现飞行器姿态控制。针对四旋翼飞行器的耦合问题,文献[4]提出了一种动态逆策略[4]。为克服模型精确性和大风干扰对飞行器飞行姿态的影响,一些文献讨论了基于神经网络的控制器设计方法[5～8]。

然而,这些方法大多基于系统物理模型进行设计的,但四旋翼在飞行过程中,不仅受到重力、空气动力和陀螺效应等多种物理效应作用外,还受制于气流等外部环境干扰[9～10],飞行器的精确物理参数无法得到,难以建立准确的物理模型,而模型的不精确又会给控制效果带来不利的影响。使得传统的基于物理模型的四旋翼姿态控制设计方法在实际应用时具有局限性。为了更好地描述四旋翼飞行器的非线性动态特性,可采用RBF-ARX模型的非线性建模方法。RBF-ARX模型是高斯径向基函数网络(RBF)和线性ARX(AutoRegressive model with exogenous variable)模型结构相结合的复合结构,是一种离线辨识的全局模型,兼具RBF网络对非线性函数逼近精度高、学习速度快和ARX模型结构简单、应用方便的优点,比较适合复杂非线性系统的控制问题,而LQR(linear-quadratic regulator)控制器是一种结构简单、易于实现的基于模型的控制器。

为此,提出了一种基于RBF-ARX模型的自适应LQR控制方案。采用结构化非线性参数优化方法辨识模型参数,得到满足工程精度要求的四旋翼非线性动态RBF-ARX模型。基于该模型通过求解工作点的Riccati方程,得到该区间内状态反馈矩阵,设计了具有状态反馈的LQR控制器,最终使得飞行器在其整个状态空间内良好运行。

2 四旋翼飞行器控制系统

本文以四旋翼飞行器实验平台作为研究对象,型号是固高GHP3001,如图1所示,采用GT-400-SV运动控制器,电机采24V5000RPM永磁直流电机,该物理平台可以用来检验各种建模方法和控制算法在四旋翼飞行器中的应用。为保障飞行器运行过程中无损,固定了飞行器的三个自由度。其飞行动力由4个独立直流电机带动的相应旋翼提供,控制电机电压可改变旋翼转速,4个旋翼中有3个是水平放置的,它们决定飞行器的俯仰角pitch(绕Y轴旋转)和翻转角roll(绕X轴旋转)输出,这两个输出角范围为-150～150(rad),还有一个竖直安装,用来控制飞行器的巡航角yaw(绕Z轴旋转),该输出可以为任意角。该系统是一个具有4输入3输出的非线性耦合系统。对于飞行器来说基本的姿态控制包括飞行器的前进后退和左右平移。

3 RBF-ARX模型的辨识和结果分析

3.1 RBF-ARX模型结构

Deng等提出了一个离散时间线性时不变模型来逼近飞行器的连续时间非线性的动态模型[11],基于这个辨识模型设计了输出状态反馈控制器,本文尝试用多个线性ARX模型来描述四旋翼飞行器的全局非线性模型,期望得到比物理模型更好的精度。对于多输入多输出的非线性系统,可将非线性区划分若干局部线性区,局部线性区可采用式(1)的ARX模型来描述:

Y(t)=f(Y(t-1),…,Y(t-ka),U(t-1),…,

U(t-kb),V(t-1),…,V(t-kc))+ε(t)

(1)

其中:Y(t)∈Rn为输出,U(t)∈Rm为输入,ε(t)∈Rn为白噪声序列,定义变量:

X(t-1)= [Y(t-1),…,Y(t-ka),U(t-1),…,

U(t-kb),V(t-1),…,V(t-kc)]T

(2)

模型(1)可写成:

Y(t)=f(X(t-1))+ε(t)

(3)

模型(3)可以看成是一个具有函数系数的ARX模型,可看出,模型(3)的依存于状态的函数系数问题实际上是一个函数逼近问题,即将多维输入空间X转换成一维的向量空间wi=πi(X)。可采用神经(RBF)网络逼近非线性矢量函数的方法,RBF网络描述非线性系统动态特性效果优良。对于多变量的四旋翼飞行器的RBF-ARX模型描述如下:

(4)

(5)

(6)

确定一组合适的状态矢量,可将式(6)转换成状态空间模型,定义状态变量如下:

确定式(6)中的w(t)后,其对应的局部线性状态空间模型方程为

(7)

其中:

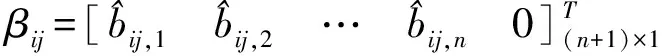
χ=[1 0 … 0]1×(n+1)

3.2 系统模型的辨识和结果分析

为了验证RBF-ARX模型的有效性,采样四旋翼飞行器在基于物理模型LQR控制的实时运行的全局数据来辨识和测试模型。四旋翼飞行器RBF-ARX模型的阶次可利用比较AIC值的方法来选取。针对研究本体,AIC计算方法为[12]

(8)

图2 俯仰角实际输出与模型输出结果

图2～图4所示为四旋翼飞行器采用RBF-ARX模型后对测试数据的建模结果。图2中,y1(t)、ym1(t)分别为飞行器俯仰角实际输出和模型输出,error1代表俯仰角实际和期望输出的误差,单位是rad,histogram1代表应残差直方图反映误差的分布情况。同理,图3和图4分别代表翻转角和巡航角模型输出精度,显然,RBF-ARX模型下系统实际输出能很好的跟随期望输出,误差波动范围小且成高斯状分布,表明模型比较理想,建模精度优良,能很好地描述飞行器系统的全局非线性动态特性。

图3 翻转角实际输出与模型输出结果

图4 巡航角实际输出与模型输出结果

4 基于RBF-ARX模型的LQR控制策略和控制结果分析

4.1 基于RBF-ARX模型的LQR控制策略

根据图5局部线性状态空间LQR控制器的设计思路,利用多变量RBF-ARX模型可以方便地在任意工作点处局部线性化的优点,采用基于局部线性ARX模型设计LQR控制器的方法,设计出了基于局部线性状态空间模型的无限时间状态调节器。

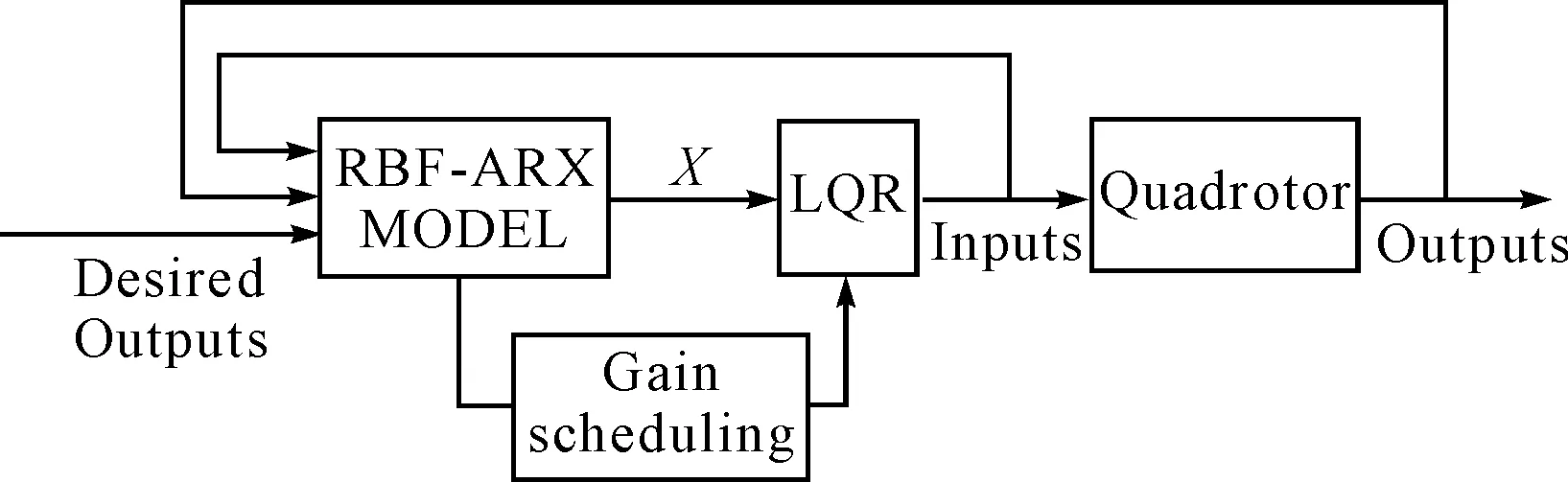
图5 基于RBF-ARX模型LQR控制器结构图

由于多变量RBF-ARX模型是一个时变全局非线性模型,所以,基于多变量RBF-ARX模型的全局LQR控制器,实际上是一种基于局部线性化模型的无限时域预测控制器。引入最优控制的性能指标作为目标函数,即设计一个输入量ΔU(k),使得

(9)

为最小,其中Q>0,R>0分别为对状态变量和输入变量的加权矩阵,表示目标函数中动态偏差和控制作用的相对重要性。相对较大的权,意味着对目标函数中对应项的较大限制。据实际要求为实现对系统的最佳控制,需在输出控制输出间找寻一个最优平衡点。使得如上性能指标最小化,可由Riccati方程在某个工作点求解P:

-pA-ATp+pBR-1BTp-Q=0

(10)

得到对称定常矩阵P,进而得到该工作点处的状态反馈增益矩阵:

K=R-1BTA-T(P-Q)

(11)

最后得到在该工作点处的状态反馈最优控制律

(12)

4.2 基于RBF-ARX模型LQR实时控制结果

通过RBF-ARX模型的辨识及仿真结果已经看出其卓越的建模精度,基于RBF-ARX模型的全局LQR控制策略不仅在局部工作区间控制精确,在全局工作区间具有很强的自适应性,因为基于RBF-ARX模型的全局LQR控制策略可看成是由多个局部线性模型和多个局部LQR控制器组成,在相邻两个釆样点处控制器的控制率的变化具有平滑连续性。通过实时控制实验进一步说明该方法的优越性。图5～图6为基于RBF-ARX模型的LQR控制器的实时控制结果,为进一步证明该模型的优越性,将基于ARX模型的LQR控制器的实时控制结果(图8所示)进行对比。

图6和图7分别是四旋翼飞行器基于RBF-ARX模型的实时控制输出和输入曲线,图6中括号内的三个值分别是俯仰角、翻转角和巡航角的控制目标值,箭头指定控制目标的时间区间,实线是俯仰角(PITCH)变化曲线,虚线是翻转角(ROLL)变化曲线,点线是巡航角(YAW)变化曲线。

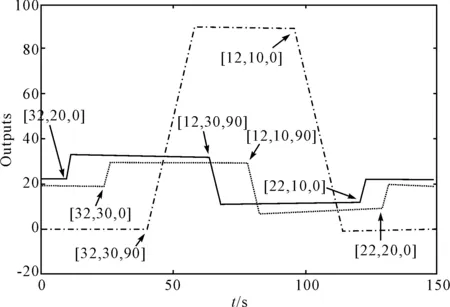
图6 基于RBF-ARX模型的实时控制输出曲线

图7 基于RBF-ARX模型的实时控制输入曲线

图8 基于ARX模型LQR实时控制输出结果

图6中四旋翼首先处于水平悬停姿态,即:俯仰角(p)、翻转角(r)和巡航角(y)分别为22、20和0;在10s处,控制俯仰角由初始值22变为32,保持翻转角和巡航角不变;在40s处,控制翻转角由初始值20变为30,保持俯仰角和巡航角不变;在70s处,控制巡航角由初始值0变为90,保持俯仰角和翻转角不变;根据控制目标依次分别改变三个输出角,维持一段时间后,控制四旋翼飞行器达到另一目标飞行姿态,并保持一段时间,最终使四旋翼飞行器回到初始水平悬停状态。图6曲线显示,初始悬停状态就很稳定,没有抖动和超调,当输出姿态角按照控制目标分别变化时,动态过程响应迅速,并且几乎没有超调,稳定后输出非常平稳,基本没有震荡和超调。

为进一步证明RBF-ARX模型的优越性,对比图8所示的基于ARX模型的LQR控制器的实时控制结果,可看出该模型下尽管稳态振荡和超调不是很大,但初始状态有很大的震荡,由此可见,基于RBF-ARX模型的实时控制更胜一筹。

为证明基于RBF-ARX模型的LQR控制策略具有更强的适应性,控制3个输出根据目标在同一时刻改变飞行姿态,并保持一段时间,最终恢复初始水平悬停姿态。图9和图10分别显示了基于物理模型和RBF-ARX模型下完成同一控制目标的效果。从图9所示的基于物理模型的LQR实时控制曲线可以看出,在初始水平悬停姿态,输出曲线有较大的震荡;飞行器目标姿态突然变化后,虽然动态响应迅速,但超调较大,稳定到新姿态后稳态特性尚可;稳定一段时间重新回到初始水平悬停状态,输出曲线又出现了存在较大超调和振荡。原因是物理模型参数不够精确,是一个简化的模型,并且旋翼的非线性动态特性被简化为线性,无法保证在所有姿态下的控制都表现良好。

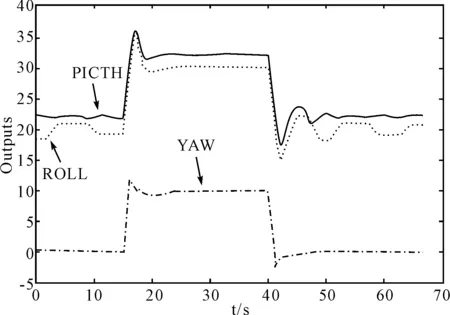
图9 基于物理模型的LQR实时控制效果

图10 基于RBF-ARX模型组的LQR实时控制效果

图10为基于ARX模型组的LQR实时控制曲线,相比图9,该建模及控制方法取得了较好的控制效果。在初始悬停位置,输出曲线震荡在很小幅度内,到达稳态后基本平稳,没有出现大幅震荡现象;控制输出姿态角突然变化后其动态反应迅速,超调量明显比基于物理模型的控制策略小得多;回到初始水平悬停姿态后,并未出现大的振荡和超调现象。

总之,基于RBF-ARX模型的LQR控制器在非线性的四旋翼飞行器的应用效果十分显著,该方法在实际工程应用领域是可行的。

5 结语

针对非线性和强耦合的四旋翼飞行器,提出了一种基于RBF-ARX模型的LQR控制方法。通过建立该模型并采用离线的方法辨识参数,通过仿真分析证实该模型具有较高精度。基于该模型设计了双闭环状态反馈LQR控制器,实际上是一种基于局部线性化模型局部控制器的无限时域预测控制器,通过实时控制结果分析,该方法控制效果显著,并与基于物理模型和ARX模型的控制结果对比,结果显示,基于RBF-ARX模型的LQR控制方法控制效果更佳,从而证实该方法的有效性和卓越性。

[1] Bouabdallah S, Noth A, Siegwart R. PID vs LQ Control Techniques Applied to an Indoor Micro Quadrotor[C]//Proceedings of the IEEE International Conference on Intelligent Robots and Systems. Sendai, Japan,2004:2451-2456.

[2] Tayebi A, McGilvray S. Attitude stabilization of a VTOL quadrotor aircraft[J]. IEEE Transactions on Control Systems Technology,2006,14(3):562-71.

[3] Bouchoucha M, Tadjine M, Tayebi A, et al. Step by step robust nonlinear PI for attitude stabilisation of a four-rotor maniaircraft[C]//16th Mediterranean Conference on Control and Automation. Ajaccio,2008:1276-1283.

[4] Das A, Subbarao K, Lewis F. Dynamic inversion with zero-dynamics stabilisation for quadrotor control[J]. IET Control Theory & Applications,2009,3(3):303-314.

[5] Guenard N, Hamel T, Mahony R. A Practical Visual Servo Control for an Unmanned Aerial Vehicle[J]. IEEE Transactions on Robotics,2008,24(2):331-340.

[6] Morel Y, Leonessa A. Direct adaptive tracking control of quadrotor aerial vehicles[C]//Florida Conference on Recent Advances in Robotics, Miami, Florida,2006:1-6.

[7] Nicol C, Macnab C, Ramirez-Serrano A. Robust neural network control of a quadrotor helicopter[C]//Canadian Conference on Electrical and Computer Engineering,2008:1233-1238.

[8] Dierks T, Jagannathan S. Neural network output feedback control of a quadrotor UAV[C]//47th IEEE Conference on Decision and Control. Cancun,2008:3633-3639.

[9] Dunfied J, Tarbouchi M, Labonte G. Neural network based control of a four rotor helicopter[C]//IEEE International Conference on Industrial Technology,2004:1543-1548.

[10] 朱君.四旋翼无人飞行器控制系统设计及控制方法研究[D].呼和浩特:内蒙古科技大学硕士学位论文,2012. ZHU Jun. Design and control method for the control system of four rotor unmanned aerial[D]. Huhhot: Master’s degree thesis of technological University of Inner Mongolia,2012.

[11] Deng X, Schenato L, Sastry S. Mode1 identification and attitude control for a Micromechanical flying insect including thorax and sensor models[C]//Proceedings of IEEE International Conference on Robotics and Automation,2003:1152-1157.

[12] 秦宣云,卜英勇,夏毅敏.基于AIC准则优化的径向神经网络微地形曲面重构[J].中南大学学报(自然科学版),2004(10):815-819. QIN Xuanyun, BU Yingyong, XIA Yimin. Micro terrain surface’s reconstruction based on the RBF neural network of AIC criterion optimization[J]. Journal of Central South University(Natural Science Edition),2004(10):815-819.

LQR Control for A Quad-Rotor Helicopter Based on RBF-ARX Mode

LIU Lili1,2ZUO Jihong1,2WU Jun1,3

(1. School of Information Science and Engineering, Central South University, Changsha 410083)(2. College of Hunan Railway Professional Technology, Zhuzhou 412001)(3. School of Electrical and Information Engineering, Changsha University of Science & Tehcnology, Changsha 410083)

For the quad-rotor helicopter which is nonlinear and coupled with each other, the design of LQR controller on quad-rotor helicopter based on RBF-ARX mode are discussed. The structure of the quad-rotor helicopter’ RBF-ARX model based on dynamic properties is built firstly, and the model parameters is identified using the off-line nonlinear parameter optimization methods, the quad-rotor helicopter’s nonlinear dynamic model is obtained to meet the demand of engineering precision.then, the state feedback ‘s LQR controller based on the model is given, and by solving the Riccati equation of working point, the state feedback matrix is accessed. Finally, the simulation results and real time attitude control verify the validity and feasibility of the proposed method.

quad-rotor helicopter, nonlinear, attitude control, state feedback, real time control Class Number TP391.9

2016年10月13日,

2016年11月11日

2015年度国家自然科学基金“抗参数横揺的欠驱动船舶航迹跟踪控制研究”(编号:61403045);2015年度湖南省教育厅科学研究资助项目“四旋翼飞行器的建模及控制策略的研究”(编号:15C0903)资助。

刘丽丽,女,硕士研究生,讲师,研究方向:复杂非线性系统建模及控制方法。左继红,男,硕士研究生,讲师,研究方向:复杂非线性系统建模及控制方法。

TP391.9

10.3969/j.issn.1672-9722.2017.04.014