基于改进阈值的管道异常状况信号降噪研究*
周成江 吴建德,2 杨静宗,2
(1.昆明理工大学信息工程与自动化学院 昆明 650500)(2.云南省矿物管道输送工程技术研究中心 昆明 650500)
基于改进阈值的管道异常状况信号降噪研究*
周成江1吴建德1,2杨静宗1,2
(1.昆明理工大学信息工程与自动化学院 昆明 650500)(2.云南省矿物管道输送工程技术研究中心 昆明 650500)
针对矿浆管道输送系统异常状态下的检测信号含有不规则噪声,且硬阈值降噪会在不连续点处产生Gibbs效应,软阈值降噪会导致小波系数与信号之间误差增大。通过选取适合的小波函数、确定分解的层数、选取适合的阈值模型,分别用软阈值与硬阈值降噪法进行降噪,并对阈值进行改进,信噪比和降噪误差得到明显改善。通过改进的软阈值与硬阈值降噪法对矿浆管道堵塞信号进行降噪处理,结果表明,改进的硬阈值和软阈值降噪方法具有更好的降噪效果。
矿浆管道; 小波变换; 信号降噪; 改进阈值
1 引言
20世纪50年代,在国外的铁精矿、煤矿等物料输送工程中,长距离矿浆管道输送以其可持续作业性、安全性、经济性引发了普遍的关注。70年代开始,长距离矿浆管道输送在国内蓬勃发展,国内较大的铁精矿、煤矿矿山陆续修建浆体管道,投入生产物料运输并取得瞩目的经济效益。21世纪,大红山矿物输送管道建成投产,我国长距离矿浆管道输送取得巨大进步,前景十分可观。但是,管道运行受到泄露、堵管、加速流等问题威胁,管道运输安全状态监控与故障识别及修复显得至关重要。
长距离矿浆管道水力输送在矿浆管道安全状态检测过程中,基于加速度、超声波等传感器的检测信号受外界地形及环境因素的影响,常混入随机噪声干扰[1]。如在管道泄露、管道堵塞、高压隔膜泵隔膜损坏、单向阀故障、停泵等故障信号采集过程中,会不同程度混入外界噪声信号,淹没有用故障信号,给故障诊断带来困难,导致故障诊断错误及故障程度误判,带来严重经济损失。因此,在矿浆管道安全状态检测过程中,对传感器采集的震动、声音、浆体流速等信号进行有效降噪处理,是一项具有重要意义的工作。
目前,对长距离矿浆管道故障信号进行降噪的研究较少。赵晶对小波函数和分解层数进行对比选取,用小波降噪实现管道裂纹信号超声信号的降噪[2]。陈浩用小波对管道泄露的负压波信号进行降噪,并对降噪信号进行分析,实现对管道泄露位置的定位[3]。崔旭伟运用Hilbert-Huang和小波对管道泄漏点产生的次声波信号进行处理[4]。刘涛用db4小波与马尔科夫原理,对管道的损坏信号进行特征识别,特征提取效果明显[5]。但是,长距离矿浆管道故障状态下的管道堵塞信号是不规则噪声,该噪声具有复杂性与非平稳性,且矿浆管道故障信号的去噪多为基于传统阈值的方法,并未对小波函数选取及分解层数进行讨论,降噪效果不理想。因此本文先以受到随机噪声污染的信号为研究对象,分析了使用不同小波函数、不同分解层数、使用软阈值与硬阈值处理的信号降噪效果,最终提出选定小波函数与分解层数下的阈值改进的信号降噪方法,大幅提高了降噪效果。使用此种改进阈值的小波降噪法对中国西部某矿浆管道堵塞信号进行降噪,为管道故障的后续研究奠定了基础。
2 小波阈值降噪原理
2.1 小波降噪原理
检测信号受到检测设备误差及外界环境干扰,都存在噪声污染。工业生产中传感器所采集的污染信号有多奇异点、非平稳性、非线性等特点[6]。该类信号模型为式(1):
s(t)=f(t)+σ*e(t)t=0,1,…,n
(1)
式中,s(t)是原信号,f(t)是真实信号,σ是噪声水平,e(t)是噪声。
对原信号进行N层分解,有用信号分解得到的小波系数比较少、幅值大,噪声信号分解的小波系数较多、幅值小,因此对小波系数设置门限处理,处理后进行信号重构。
2.2 小波降噪步骤
1) 对小波函数进行对比选择,分解层数N的选取,信号S按选择的小波函数与分解层数进行分解;
2) 使用软阈值法和硬阈值法,并对阈值进行改进,对第一层到第N层高频进行处理;
3) 将低频的第N层和高频第一层到第N层,进行一维重构。
小波降噪步骤如图1所示。

图1 小波降噪步骤
3 小波阈值降噪方法
小波默认阈值一般计算量很小、实现比较简单、运用比较普遍,但降噪效果较软阈值与硬阈值差。小波降噪阈值选择具有很高的复杂性,并且信噪比很大程度取决于阈值选择的优劣[7],尽管donoho声称找到最优的小波降噪阈值,但是工程信号降噪效果并不明显。
3.1 软阈值与硬阈值

估计小波系数的方法如式(2),取:
(2)
分解后小波系数的处理,可以用软阈值方法或硬阈值方法。当小波系数比阈值λ要大,硬阈值方法将其保留,其他情况则置零。表达式如式(3):
(3)
当小波系数比阈值λ要大,软阈值方法将其向零收缩,其他情况下则置零。表达式如式(4):
(4)
采用硬阈值小波变换法降噪虽然能更多地保留有用信号的尖峰特征,取得较好的降噪效果,但在阈值λ与-λ处不连续,小波重构过程会伴随不规则震荡[8],导致信号的光滑性丢失;软阈值小波变换法降噪处理噪声信号更为平滑,且在阈值处连续,但是小波系数的估计值与分解值之间存在偏差,信号逼近程度受到影响。
3.2 改进软阈值与硬阈值
由软阈值与硬阈值小波变换方法对比可知,选择合适阈值在信号降噪过程中至关重要,如果阈值过小,不能有效去除噪声污染,要是选择阈值过大,有用信息及特征会被删除,增大降噪误差。因此对软硬值与硬阈值降噪方法进行改进[9]。表达式如式(5):
(5)

3.3 降噪效果判定
对于信号的降噪效果,最有效的权衡指标为信噪比(SNR)和均方根误差(RMSE)。计算公式如式(6):
(6)
式中x(n)为原信号,x′(n)为经处理后的估计信号。信噪比(SNR)越高,均方根误差(RMSE)越小,则降噪的效果越好。
4 小波阈值降噪分析
4.1 不同小波函数降噪仿真
信号降噪的效果随着小波函数选择的不同存在很大的差异性,一般来说,若小波有很好的对称性则不会产生相位畸变,若小波有很好的正则性,则降噪后更能还原光滑的波形[10]。由于实验数据为离散数据,因此分析噪声信号在Haar、Daubechies、Symlets、和Biorthogonal四种离散小波系下的降噪效果。在Matlab中选用的信号为Bumps冲击信号,如图2所示,加噪后的信噪比为30.6988,均方根误差为1.0079。如图3和表1所示,图中横坐标为采样点数,纵坐标为信号的振幅,该加噪信号经离散小波函数的处理,得出相应波形及信噪比与均方根误差。

图2 原信号及加噪信号

图3 四种离散小波处理

表1 四种离散小波降噪效果对照表
通过分析图3和表1,可得出结论,在非平稳离散信号降噪之前对小波函数的选取至关重要,且Sym6小波函数对离散信号的降噪信噪比(SNR)较高、均方根误差(RMSE)较低、效果较为明显。
4.2 不同分解层数降噪仿真
对于小波滤波而言,小波分解的层数直接决定滤波效果的好坏,在不同信噪比的情况下,不同信号都存在降噪效果较好的分解层数。因此,不同层数对小波去噪效果有很大的差异性,选择合适的层数能获得较好的降噪效果。基于选定的Sym6小波函数进行不同层数降噪分析如图4、图5和表2所示。

图4 一至四层小波分解

图5 四至八层小波分解

表2 不同层数降噪效果对照表
通过以上不同层数小波变换对非平稳噪声降噪后的波形图及信噪比和均方根误差,可得出结论,在非平稳离散信号降噪过程中,小波分解层数选择至关重要,降噪效果随小波分解的层数增加而变好,但并非分解层数越多,降噪效果越好,当信号分解后的频带信号与噪声的等级存在差异较少时,再加层数,降噪效果保持不变甚至变差[11]。由表2可得,当层数大于6层后,对降噪效果改善并不明显,反而使得计算迭代变得更加复杂。
4.3 不同阈值降噪仿真
对于离散非平稳信号小波降噪而言,阈值选取方法及阈值量化方法尤为重要,因为随机噪声的方差具有未知性,降噪时要对阈值进行估计。Matlab提供了基于样本估计的阈值的四种选取方法,即极大极小阈值(minimaxi)、固定阈值(sqtwolog)、启发式阈值(heursure)、自适应阈值(rigrsure)。选定Sym6小波函数、在软阈值的基础上进行6层分解,得到波形图如图6,去噪效果见表3。
通过分析样本估计的不同阈值降噪的波形及降噪效果,可得出结论,在非平稳离散信号小波降噪中,基于样本估计的不同阈值降噪效果差异并不十分明显,相比之下,软阈值函数前提下,启发式阈值(heursure)降噪信噪比较高,效果较好。

图6 不同阈值降噪

表3 各阈值降噪效果对照表
4.4 软、硬阈值及改进阈值降噪仿真

图7 不同阈值法降噪
在实际的信号降噪研究中,软阈值法与硬阈值法使用较多,同时能获得较好降噪效果。硬阈值法虽能更多地保存有用信号的尖峰特性,但是小波重构时可能产生震荡。软阈值法虽在阈值处具备很好的连续性,但分解的系数与估计的系数存在很大偏差,致使重构信号到真实信号的逼近受到很大影响。在软硬阈值存在的缺陷的基础上,用一种新的阈值处理方法,引入一组阈值式(5),并引入一个参数α,取0<α<1,最终取阈值为3.9618,使得既能够使信号最大限度地保存真实信号,又能保持信号的平滑性。选定Sym6小波函数、启发式阈值(heursure)、6层分解,得到的波形如图7,降噪效果见表4。

表4 不同阈值法降噪效果对照表
通过以上软阈值方法、硬阈值方法以及改进阈值方法对信号降噪处理的波形图和效果分析,可得出结论,软阈值法、硬阈值法已经具备良好降噪效果,硬阈值法信噪比已高达62.43,基于改进阈值的方法降噪效果优于软硬阈值降噪法。
5 矿浆管道堵塞信号降噪
矿浆管道堵塞信号为一维离散信号,该离散信号为非平稳信号。因此,在小波函数多样性的基础上,先对小波函数进行分析,选择降噪效果较好的6阶Symlets离散小波、再分析信号分解到不同层数的降噪效果,选择Sym6小波做5层分解,然后分析基于样本估计的4种阈值选取方法,选择启发式阈值(heursure)法,最后分别用软阈值法、硬阈值法、改进阈值法对信号进行降噪处理,比较得到较好降噪效果。然后使用以上处理过一维非平稳离散信号的方法对传感器采集到的矿浆管道堵塞信号进行降噪处理,得到如图8所示的波形图,取得良好的降噪效果。
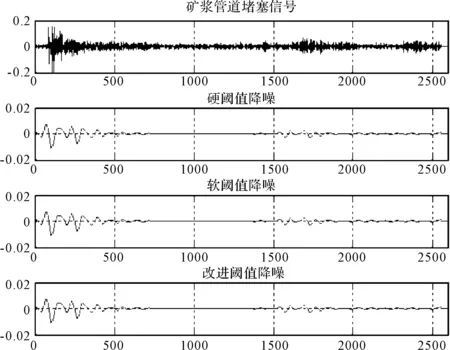
图8 管道堵塞信号改进阈值降噪
6 结语
使用Bumps信号分析非平稳离散信号的降噪问题,对影响降噪性能的小波函数、分解层数、阈值选取等主要因素做波形的仿真分析及降噪效果的对比。通过对比找出较好的降噪方法,再对阈值方法进行改进,使降噪效果进一步提高。最终使用得出的非平稳离散信号的软阈值法、硬阈值法及改进阈值法对矿浆管道堵塞信号进行降噪处理,得到很好的降噪效果。本文的研究为矿浆管道堵塞信号的特征提取提供支撑,为矿浆管道输送系统故障信号处理提供参考,具有十分重要的实际意义。
[1] 常广,胡铁华,刘锐,等.一种硬阈值与软阈值结合的小波降噪新方法[J].机电产品开发与创新,2015,6:69-71. CHANG Guang, HU Tiehua, LIU Rui, et al. A New Wavelet Denoising Method Combining Hard Threshold and Soft Threshold[J]. Development & Innovation of Machinery & Electrical Products,2015,6:69-71.
[2] 赵晶.管道腐蚀裂纹超声内检测信号处理研究[D].北京:北京化工大学,2008. ZHAO Jiang. Pipe corrosion cracking with ultrasonic detection signal processing research[D]. Beijing: Beijing University of Chemical Technology,2008.
[3] 陈浩.流体运输管道泄漏负压波模拟与信号处理研究[D].大庆:东北石油大学,2012. CHEN Hao. Research on Negative Pressure Wave Simulation and Signal Processing of Fluid-Conveying Pipeline Leak[D]. Daqin: Northeast Petroleum University,2012.
[4] 崔旭伟.管道泄漏信号的特征提取方法研究[D].大庆:东北石油大学,2015. CUI Xvwei. A Study on the Method of Pipeline Leakage Signal Feature Extraction[D]. Daqin: Northeast Petroleum University,2015.
[5] 刘涛.管道检测系统中的信号处理技术研究[D].天津:天津大学,2007. LIU Tao. Research on signal processing technology in pipeline detection system[D]. Tianjin: Tianjin University,2007.
[6] 向晓燕,谭子尤,张书真,等.基于小波的阀值消噪方法讨论及实现[J].现代电子技术,2007,17:172-173,176. XIANG Xiaoyan, TAN Ziyou, ZHANG Shuzhen, et al. Realization of Eliminating Noise Based on Wavelet[J]. Modern Electronics Technique,2007,17:172-173,176.
[7] 聂林涛,张恺,等.基于小波分析的一维含噪信号的除噪方法[J].四川兵工学报,2011,12:86-88.
NIE Lingtao, ZHANG Kai, et al. Denoising method based on wavelet analysis for one dimensional noise signal[J]. Journal of Sichuan Ordnance,2007,17:172-173,176.
[8] 王振江,苏新彦,程雪,等.超声波检测中的小波降噪方法研究[J].山西电子技术,2010,3:89-90. WANG Zhenjiang, SU Xinyan, CHENG Xue, et al. De-noising with Wavelet Technology in Ultrasonic Testing[J]. Shanxi Electronic Technology,2010,3:89-90.
[9] 王芳,刘祖润,吴海辉,等.基于软硬阈值折中的小波包语音增强算法的研究[J].铁路计算机应用,2010,7:8-10. WANG Fang, LIU Zurun, WU Haihui, et al. Speech enhancement algorithm based on compromise for soft and hard thresholds[J]. Railway Computer Application,2010,7:8-10.
[10] 赵建昌,刘爱平,尚歆,等.基于小波重构的脉动风合成及特性研究[J].振动与冲击,2008,6:140-143,193. ZHAO Jianchang, LIU Aiping, SHANG Xin, et al. Synthesis and Characteristic of Fluctuating Wind Based on Wavelet Reconstruction[J]. Journal of Vibration and Shock,2008,6:140-143,193.
[11] 薛海建,郭晓松,周召发,等.基于小波阈值改进算法的动调陀螺信号去噪[J].计算机测量与控制,2012,10:2785-2787. XUE Haijian, GUO Xiaosong, ZHOU Zhaofa, et al. Dynamically Tuned Gyro Signal Denoising Based on Improved Wavelet Threshold Arithmetic[J]. Computer Measurement & Control,2012,10:2785-2787.
Signal Denoising of Abnormal Condition of Pipeline Based on Improved Threshold
ZHOU Chengjiang1WU Jiande1,2YANG Jingzong1,2
(1. Faculty of Information Engineering and Automation, Kunming University of Science and Technology, Kunming 650500) (2. Engineering Research Center for Mineral Pipeline Transportation YN, Kunming 650500)
The detection signal of slurry pipeline transportation system contains irregular noise under the abnormal state, the hard threshold de-noising produced Gibbs effect at the discontinuity point and soft threshold de-noising caused the error between the wavelet coefficient and the signal. By selecting the suitable wavelet function and comparing the decomposition of the number of layers, selecting the most suitable threshold model and soft threshold method and hard threshold method are used to reduce the noise and the threshold is improved, signal to noise ratio and noise reduction error are obviously improved. Improved soft threshold method and hard threshold method are used to deal with slurry pipeline jam signal. The results show that improved hard threshold and soft threshold method has better noise reduction effect.
slurry pipeline, wavelet transform, signal denoising, improved threshold Class Number TN911.4
2016年10月17日,
2016年11月27日
国家自然科学基金项目(编号:51169007);云南省科技计划项目(编号:2013DH034)资助。
周成江,男,硕士研究生,研究方向:故障诊断及工业智能控制。吴建德,男,教授,博士生导师,研究方向:矿物管道输送实时检测与控制。杨静宗,男,博士研究生,研究方向:复杂工业过程的建模分析与控制。
TN911.4
10.3969/j.issn.1672-9722.2017.04.002

