士兵综合素质评价模型研究*

李佳雨 黄旭东 于战科 郝 欢

(1.湖北省黄石军分区 黄石 435002)(2.95100部队 广州 510000)(3.解放军理工大学通信工程学院 南京 210007)

士兵综合素质评价模型研究*

李佳雨1黄旭东2于战科3郝 欢3

(1.湖北省黄石军分区 黄石 435002)(2.95100部队 广州 510000)(3.解放军理工大学通信工程学院 南京 210007)

为打赢新世纪信息化战争,军队对士兵的素质要求不断提高,对士兵进行综合素质评价的需求日益凸显。但我军目前尚未形成完善的士兵综合素质评价方法,且其他行业现有的综合素质评价方法客观性、通用性不足,不能直接应用于军队。针对这一问题,在采用层次分析法建立评价指标体系的基础上,提出采用最小二乘数学模型确定评价指标权值的方法,构建出士兵综合素质评价模型。该模型具有客观性、科学性、准确性和通用性等特点。

士兵; 综合素质; 评价模型; 权值

1 引言

人是战争胜负的决定因素。随着科学技术迅猛发展并应用于军事,人类战争已不可避免地由传统的机械化作战形式向信息化战争转变。为适应新的战争形态,打赢信息化战争,军队对士兵的素质要求早已超越“米、秒、环”等最基本的训练成绩,在不同素质指标方面提出了更高要求。然而,在高技术、信息化战争早已打响多次的现实情况下,我军目前依旧还未形成完善的士兵综合素质评价方法。军事实力是经济快速稳定发展的重要保证,在世界新军事变革的汹涌浪潮下,构建科学合理的士兵综合素质评价机制,促进部队更加科学合理地编配士兵,提高部队战斗力显得更加紧急迫切。因此,本文的研究具有重要的现实意义。

2 士兵综合素质评价现状

美军具有较完整的士兵素质研究和培养体系[1～2],国内一些政府部门和企业也早已建立起了员工素质评价制度,但国内对于我军士兵综合素质评价仍主要停留在理论研究和简单应用的层面。

新兵入伍后,一些单位的作训或士兵管理部门都会对本单位新兵进行综合素质评价。但受限于工作任务繁重、缺乏专业人才等因素,部队对士兵综合素质评价存在一些误区,主要表现在两个方面。一是单一指标片面评价,这种方法是将每个指标的数据与往年相应指标数据进行对比,并针对每个指标逐一给出结论。但实际上,利用这种方法得出的只是单个指标的结论,并不能反映这批士兵整体的素质高低,也无法反映出单个战士的综合素质水平,且忽视了某些指标之间的关联性,得出的结论不够科学准确。二是多指标等权重评价,这种方法是指某些单位采用层次分析法,对多个指标等权重的进行综合评价,没有对指标的权重进行区分,其结果可能会因为指标本身的重要程度不同而出现差错,从而得到不够科学准确的评估。

文献[3]采用层次分析法(AHP)对评价指标进行层次划分,采用Fuzzy-AHP算法确定权值,提出了较为完善的士兵综合素质评价系统。但利用该系统对任何一个评价对象进行评价时,都需要专家再次打分进行数据采集,没有形成一个独立完整的评价系统。

3 模型构建

构建士兵综合素质评价模型,主要包括建立士兵综合素质评价指标体系和确定评价指标权值两方面工作。

建立评价指标体系的一般性做法是采用层次分析法。但是不同任务性质的部队,士兵综合素质评价指标体系有所不同。出于保密考虑,本文仅以一个简单的评价指标体系为例(图1),重点分析确定权值的方法。

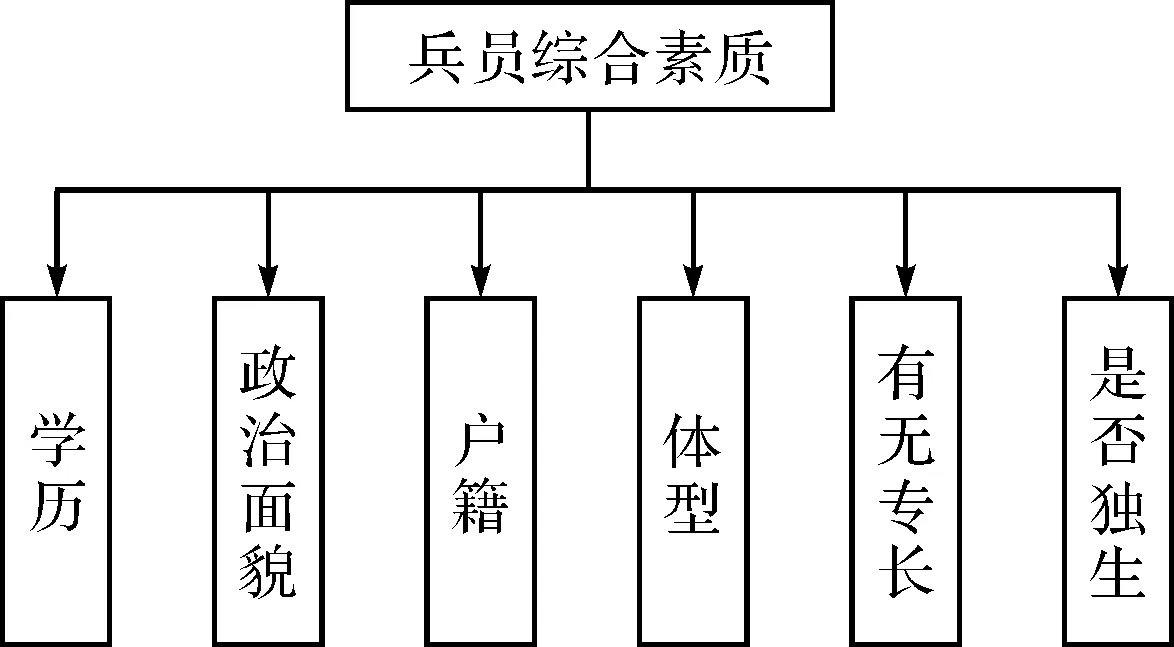
图1 士兵综合素质评价指标体系

4 权值研究

确定权值的方法多种多样,文献[4]中列举了12种传统的权值确定方法,这些方法大多是从评价指标入手进行分析,得出权值后再计算出综合得分,客观性不足。近年来,人工智能算法逐步被引入到权值确定中来,取得了一些研究成果,但处理离散数据的准确性还存在不足[5]。

通过专家对每个评价对象进行总体印象打分,将确定权值转化为最小二乘数学模型进行求解,能够有效克服传统方法客观性、准确性、通用性不足的缺点。

4.1 样本采集

本文以某新兵团970名新兵为研究总体,利用C++编程随机抽取其中50名新兵为样本,邀请9名荣获“新兵团带兵能手”称号的基层军官作为评分专家。为验证抽取的样本是否具有一般性和有效性,共抽取了三组50个样本的群体进行统计分析,结果表明三组样本均具有一般性和有效性。

数据采集按照以下步骤进行:

STEP 1:从总体中随机抽取N个样本。

STEP 2:设置M项评价指标,提取N个样本共N×M个指标数据。

STEP 3:邀请K名专家,依据每个样本的M项指标情况,每名专家按照给定的评语集对每个样本总体情况进行打分。本模型的评语集为{优、良、中、差}。第一名专家部分打分情况见表1。

表1 第一名专家打分情况统计表

STEP 4:将专家给定的打分数值化。对于第n个样本,有K个专家打分结果,其中第k个专家打分数值记为bn,k。

STEP 5:将每个个体的每项指标数值化。第n个样本第m项指标数值记为xn,m。

采取专家对每个样本的总体情况进行打分,而不是对每个样本的每个指标单独打分,主要是出于两方面考虑。一是熟悉士兵成长和培养的部队军官,凭积累的经验,易于根据各项指标情况给出士兵个体综合得分,却难以准确地对指标进行两两比较。在此情况下,通过军官作为专家对士兵个体进行综合打分,进而建立评价模型是科学合理的。二是通过对每个样本总体情况进行打分,规避了专家直接判断单个指标情况,减少了打分次数,降低了专家的主观判断对结果的影响程度。

4.2 量化得分

指标量化的方法很多,为了将现实问题转化为数学模型进行求解,本文主要采用“等差量化法”[6]将专家打分和六项评价指标进行量化。

1) 专家打分:对专家打分“优、良、中、差”分别赋值10、8、6、4分;

2) “学历”:对大学本科及以上、大专、高中和中专、初中分别赋值10、8.5、7、6分;

3) “政治面貌”:对党员、团员、群众分别赋值10、8、6分;

4) “户籍性质”:针对该项指标,邀请10名专家对士兵的“农业”和“非农”单指标进行打分,10名专家均认为“农业”户籍士兵表现更好,从而对“农业”和“非农”户籍分别赋值10、6分;

5) “体型”:对合格、偏胖(瘦)分别赋值10、6分;

6) “有无专长”:有无专长以是否具有国家证书为判断标准。对有专长、无专长分别赋值10、6分;

7) “是否独生子女”:针对该项指标,邀请10名专家对“独生”和“非独生”单项指标进行打分,6人认为非独生表现更好,4人认为独生表现更好。从而对“独生”和“非独生”分别赋值7.6、8.4分。

根据上述赋值原则,可得出每个样本的评价指标值和专家打分分值情况。其中第一名专家打分情况赋值后如表2。

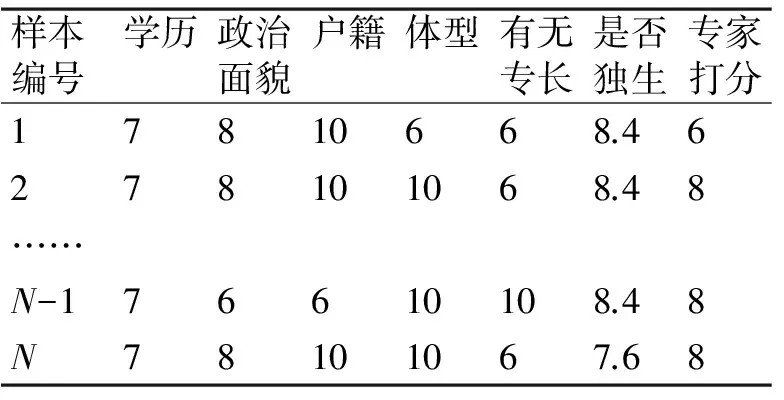
表2 第一名专家打分及评价指标赋值统计表

4.3 数学模型

定义第n个样本的原始综合得分为:去掉K名专家打分的最高和最低分后的平均值,记为bn,数学表达式为

(1)

全体样本综合得分向量为

BN×1=[b1,b2,b3,…,bN-1,bN]T

(2)

第n个样本个体各指标得分向量为

Xn=[xn,1,xn,2,…,xn,M-1,xn,M]

(3)

全体样本各指标得分矩阵为

XN×M=[X1,X2,…,XN]T

(4)

令评价指标的权值向量为

AM×1=[a1,a2,a3,…,aM-1,aM]T

(5)

且满足:

(6)

ai≥0

(7)

上述过程采集的数据具有如下关系:

XA=B

(8)

即:

=[b1,b2,b3,…,bN-1,bN]T

(9)

因此,对权值确定可以转化为求最小二乘优化问题进行求解[7]:

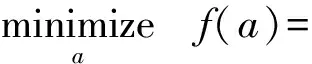
(10)

(11)

从而有:

AM×1=(XTX)-1XTBN×1

(12)

(13)

4.4 算法设计

前面已将确定权值问题转化为求最小二乘问题,只需调用Matlab中的最小二乘线性拟合函数lsqlin即可。Matlab算法为

X=[N*M];

B=[N*1];

a_eq=ones(1,M);

b_eq=1;

lb=zeros(M,1);

[a,resnorm,residual,exitflag]=lsqlin(X,B,[],[],a_eq,b_eq,lb,[]);

a

算法中的resnorm是整个结果的平方误差和,residual是对每一组数据得到的剩余误差,即XA-B,一共有N组,exitflag的值表示不同的收敛情况。

4.5 数据处理

利用上述Matlab算法求取权值,得到权值向量值AM为

AM=[0.6537,0.1421,0.0000,0.1140,0.0902,0.0000]

4.6 异常数据检测

将得到的权值代入表2,得到每个样本新的综合得分。通常情况下,样本综合得分总体上服从正态分布。利用SPSS软件,采用“单样本K-S检验法”对此进行检验,结果如表3所示。

表3 K-S检验主对话框

从检验结果来看,渐进显著性P=0.06>0.05,从而认为送检的数据服从正态分布[8]。因此可采用“3σ准则”[9]对新的综合得分进行异常数据检测[10],流程如图2所示。

图2 异常数据检测流程

(14)

3σ′=2.2659

因此,将AM作为士兵综合素质评价最终权值。

各指标权值情况如表4所示。

表4 指标权值对照表

4.7 权值分析

各指标权值饼状图如图3所示。

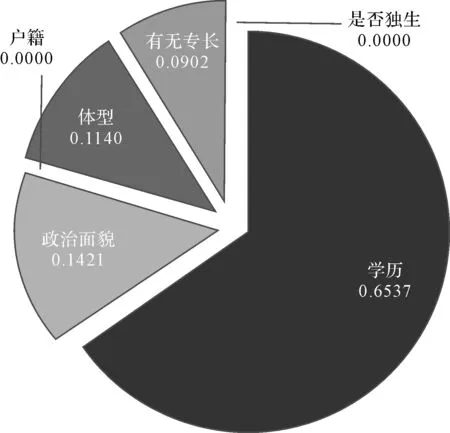
图3 指标权值饼状图

可以看出,“学历”所占权值为0.6537,在6项评价指标中占有极其重要的地位,这与国家优先征集体检政审双合格大学生士兵的政策一致。“政治面貌”所占权值为0.1421,说明士兵的政治素养也是构成综合素质的一项重要指标。“体型”和“有无专长”对综合素质评分也有一定的影响。而“户籍”权值为0,与国家取消户籍区分的政策趋势一致,且与文献[11]在实际研究中证明的农村与城镇士兵在多个方面的差异无统计学意义这一结论一致。“是否独生”权值为0,说明该部队已不再认为独生与非独生子女的整体表现有明显区别,文献[12]也得出相类似的结论,认为独生子女与非独生子女士兵比较,其整体人格特征不存在问题性差异。

通过上述分析可知,利用本文所构建的模型所得到的结果能够找到可靠的现实依据,说明本文构建的士兵综合素质评估模型具有一定的实际应用价值。此外,不同任务性质的部队,由于其需求不同,通过该模型得到的相同指标的权值应该有所不同。

5 模型应用

该模型主要可以应用于三个方面。

5.1 个体和总体素质评价

对于任意适合该模型评价的个体,都可以采用该模型进行综合评价打分。比如某个体的6项评价指标如表5所示,则其综合素质得分为8.45分,按照评语集的隶属度,可以评定其综合素质为“良”。

表5 某个体评价指标情况

计算出所有个体得分后,可以采用数理统计的方法,对总体素质情况进行评价。

5.2 士兵选拔和分配

在选拔过程中,可采用该模型对预征集的士兵进行打分排序,提高士兵征集质量。此外,还可根据不同岗位需求以及士兵各项素质指标的评价情况,将不同素质士兵科学合理分配至不同岗位。

5.3 士兵素质培养

根据评价指标的权值,对士兵的训练培养进行长期的跟踪记录以及分析,适时地、科学合理地调整对士兵的培养训练计划,进而达到有针对性地对士兵进行素质培养的目的。

6 结语

常见的权值确定方法,多是从评价指标入手进行分析确定。本文则采用最小二乘问题数学模型来确定评价指标权值,采取“逆向”的方式,通过专家对样本的综合情况进行打分,不直接分析评价指标,确保了评价指标权值的客观性、科学性、准确性。该模型的优点在于,一旦构建好模型,对于任何新个体,只需采集相关指标数据,即可得出该个体综合评价得分,无需再次邀请专家打分或者进行其他类似的评价工作,具有完全通用性和稳定性。

本文作者在实际工作中开展了评价指标体系研究,结合具体任务性质的部队构建了不同的评价模型,研究成果对士兵综合素质评价、选拔分配、能力培养具有重要指导意义。但出于保密考虑,本文仅重点介绍了评价指标权值的确定方法。下一步将利用建立的模型对评价对象进行跟踪研究,进一步验证模型的准确性。

[1] U.S. Department of Defense. Population represen-tation in the military services: Fiscal Year 2004[M]. 2006,29.

[2] 张楠.美军建立高素质士兵队伍举措的研究[J].西安政治学院学报,2008,21(2):31-33. ZHANG Nan. Research on the Establishment of High Quality Soldiers in the US Army[J]. Journal of Xian Politics Institute,2008,21(2):31-33.

[3] 刘法华.士兵综合素质评估系统研究[D].青岛:中国石油大学(华东),2010. LIU Fahua. The Rearch on Soldier Intelligence Evaluation[D]. Qingdao: China University of Petroleum(East China),2010.

[4] 王晖,陈丽,陈垦,等.多指标综合评价方法及权重系数的选择[J].广东药学院学报,2007,23(5):583-589. WANG Hui, CHEN Li, CHEN Ken, et al. Multi Index Comprehensive Evaluation Method and the Choice of Weight Coefficient[J]. Journal of Guangdong Pharmaceutical University,2007,23(5):583-589.

[5] 姚明海.改进的遗传算法在优化BP网络权值中的应用[J].计算机工程与应用,2013,49(24):49-54. YAO Haiming. Application of Improved Genetic Algorithm in Optimizing BP Neural Networks Weights[J]. Computer Engineering and Applications,2013,49(24):49-54.

[6] 詹耀祖.人力资源管理中考评指标量化技术的应用[J].辽宁经济管理干部学院学报,2012(2):19-20. ZHAN Yaozu. Application of Quantitative Techniques in the Evaluation of Human Resource Management[J]. Journal of Liaoning Economic Management Cadre College,2012(2):19-20.

[7] 丁斌,杜元.基于PSO算法与AHP最小二乘模型对多属性决策问题权重求解[J].系统工程,2010,28(7):102-106. DING Bin, DU Yuan. Multi-attribute Decision Making Problem Solving Weights Based on PSO Algorithm and AHP LS Model[J]. Systems Engineering,2010,28(7):102-106.

[8] 朱红兵,何丽娟.在SPSS10.0中进行数据资料正态性检验的方法[J].首都体育学院学报,2004,16(3):123-125. ZHU Hongbing, HE Lijuan. Method for Testing the Normality of Data in SPSS10.0[J]. Journal of Capital Institute of Physical Education,2004,16(3):123-125.

[9] Friedrich Pukelsheim. The three sigma rule[J]. The American Statisti-cian,1994,48(2):88-91.

[10] 陈斌.异常检测方法及其关键技术研究[D].南京:南京航空航天大学,2013. CHEN Bin. Research on Outlier Detection Method and its Key Techniques[D]. Nanjing: Nanjing University of Aeronautics and Astronautics,2013.

[11] 李柱,张继刚,张蕾,等.某工程部队士兵心理健康水平调查分析[J].空军医学杂志,2015,31(2):112-114. LI Zhu, ZHANG Jigang, ZHANG Lei, et al. Investigation and Analysis on Mental Health of Soldiers in an Engineering Unit[J]. Air Force Medical Journal,2015,31(2):112-114.

[12] 宋华,黄涛,纵兆辉.独生与非独生子士兵群体人格特征比较[J].中国组织工程研究与临床康复,2007,11(30):5952-5954. SONG Hua, HUANG Tao, ZONG Zhaohui. Comparison of personality characters between singleton and non-singleton soldiers[J]. Journal of Clinical Rehabilitative Tissue Engineering Research,2007,11(30):5952-5954.

Comprehensive Quality Evaluation Model of Soldiers

LI Jiayu1HUANG Xudong2YU Zhanke3HAO Huan3

(1. The Huangshi Army Distinct of Hubei, Huangshi 435002)(2. No. 95100 Troops of PLA, Guangzhou 510000)(3. Institute of Communication Engineering, PLA University of Science and Tehcnology, Nanjing 210007)

In order to win the information-based war in the new century, the army’s demands on the soldiers’ quality have been continuously improved, and the demand for the comprehensive quality evaluation of the soldiers is becoming increasingly prominent. But the army has not yet formed a comprehensive evaluation of the quality of the soldiers, and other industries existing comprehensive quality evaluation methods objectivity, lack of generality, can not be directly applied to the army. To solve this problem, based on the establishment of evaluation index system by AHP, the method of determining the weight of evaluation index by using the least square method is put forward, and the comprehensive evaluation model of soldier is established. The model has the characteristics of objectivity, scientificity, accuracy and versatility.

soldier, comprehensive quality, evaluation model, weight Class Number TP182

2016年10月8日,

2016年11月24日

国家自然科学基金青年项目(编号:71401176)资助。

李佳雨,男,硕士,研究员,研究方向:信息安全,国防动员。黄旭东,男,研究员,研究方向:部队管理。于战科,男,博士,讲师,研究方向:优化理论与方法。郝欢,男,博士研究生,研究方向:信号时频分析与处理。

TP182

10.3969/j.issn.1672-9722.2017.04.015