水下基阵大地坐标优质解算点的选择方法*

张永超 徐国贵

(91388部队94分队 湛江 524022)

水下基阵大地坐标优质解算点的选择方法*

张永超 徐国贵

(91388部队94分队 湛江 524022)

获得精确的声基阵大地坐标,对于水下目标测量和定位有着重要的意义。采用测量船定点录取声基阵测量数据时,航行轨迹一般成椭圆,取任意三个测量点利用球面交汇原理可以定位出声基阵大地坐标,但定位误差较大。根据球面交汇求解误差最小的条件,以声基阵原始数据为参考,选取椭圆航行轨迹上任一个录取点,求出以该点与声基阵原始点连线为法线并经过声基阵原始点的平面,平面与椭圆轨迹方程交两点,找出与这两点距离最近的两个测量点,即可认为这三个测量点解算声基阵坐标误差小。

声基阵; 球面交汇; 定位误差; 选点方法

Class Number TB566

1 引言

声基阵是进行目标测量和定位的重要装备,而声基阵的海底坐标测量有广泛的应用场合。对于测量声基阵大地坐标的测量一般选用时延估计的方式[1]。测量船在GPS的引导下,按预定的航路(一般成椭圆轨迹)等间隔航行,到预定的数据测量点时发射测阵询问测距声脉冲,获取所有声基阵单元的测距值及测量船相应位置GPS坐标数据,选取三个测量点利用球面交汇原理即可求出基阵的大地坐标[2]。

对于声基阵某个单元,用于解算其坐标的测量点会形成一组椭圆点。如果用所有这些测量点测量的数据去解算基阵单元,必然会降低解算的精确性。在这些点中,若有三个点满足与声基阵单元的空间夹角为90°,此时解算误差最小。故而从中挑选几组解算误差小的点来求解基阵单元,可以提高解算的精确性。文中给出一种挑选解算误差小的一组录取点的方法,该方法先拟合椭圆航行轨迹方程,选取任一个测量点A1,求出以A1与一个声基阵原始点S1(原始点S1为最初声基阵布放的初始位置)的连线为法线并经过S1的平面方程,平面与椭圆轨迹方程交两点a2、a3,只需找出与这两点距离最近的两个录取点A2、A3,即可认为这组点解算误差小。通过平面方程与椭圆方程相交公式计算说明:当椭圆轨迹短轴大于声基阵深度,必能找到至少一组解算误差小的三个点。

2 解算误差小的条件

在空间三维坐标系中,测量船上3个声源发射点A1、A2、A3到某个声基阵阵元S的距离为r1、r2、r3,如图1所示,于是有球面方程:

(1)

通过求解方程(1)得到该点阵元坐标。其中xi,yi,zi(i=1,2,3)为声源发射点A1,A2,A3的测量坐标,x,y,z为阵元点S的解算坐标；c为海水中的声速；τi为阵元接收到的CW脉冲信号和声源发射的CW脉冲信号之间的时延差[3～5]。

在实际的测量中,声基阵阵元S的位置在A1A2为直径的圆弧上交汇误差最小,即∠A1SA2为直角时定位误差最小。同理,S在A1A3为直径的大圆弧上时定位精度最高。总之,最优定位的测点位置条件为:∠A1SA2=∠A1SA3=∠A2SA3=90°[6～7]。

3 存在一组优质解算点的条件

选取一个声源点A1(CAx,CAy,CAz)和阵元测量点S(CSx,CSy,CSz),阵元测量点S是最初声基阵布放的初始位置。由于对阵元测量点S(CSx,CSy,CSz)的测量精度要求不高,它起到的作用只是寻找合适的声源点,而解算实际中的声基阵坐标,是利用测量点球面交汇原理。A1S所在的直线方程:

(2)

由方程(2)可以得到在阵元测量点S位置处与该直线垂直的平面方程:

(CSx-CAx)(x-CSx)+(CSy-CAy)(y-CSy)+(CSz-CAz)(z-CSz)=0

(3)

利用方程(3)与椭圆相交,令z=0(建立的坐标系与实际的相反,声基阵阵元在z轴上方,便于求解),可解出该平面与椭圆轨迹相交的两点a2、a3,这两点在椭圆轨迹上,满足A1Sa2构成的角与A1Sa3构成的角都为90°。然后从声源点中寻找分别与a2、a3距离最近的声源点A2、A3,这两个点即是选取的最优点。图2给出了方程(3)与椭圆相交两点a2、a3,并由这两点确定声源点的示意图[8～10]。

当椭圆轨迹短轴相对于阵的长度长,并且大于声基阵的深度时,必能满足椭圆上至少存在一点与声基阵阵元点连线为法线并经过阵元点的平面,与椭圆相交两点。

建立坐标系如图3所示。

建立过A1和S两点的空间直线L的方程:

(4)

建立以L为法线,经过点S的平面方程:

(x0-x1)(x-x1)+y0y+z0z=0

(5)

椭圆轨迹方程为

(6)

令平面z坐标为z0,则有:

(7)

(8)

若平面与椭圆相交两点,则方程(8)满足Δ>0,即;

(9)

将t与k的值带入方程(9):

(10)

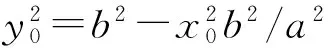
(11)

方程(11)存在满足大于0的解时,需顶点在x轴上半部分,化成顶点形式:

(12)

(13)

式(13)成立,需满足b>z0。

综上所述,在满足x0>x1时,平面与椭圆轨迹相交存在两点的条件是b>z0,即椭圆的短轴大于深度。

由上述过程可知,因垂直面的条件,∠A1SA2、∠A1SA3近似为90°,而∠A2SA3与椭圆的长短轴之比有关,当比值小于4/3接近1时(即为圆),此时∠A2SA3在90°附近变化。改变椭圆轨迹长轴的值,可以寻找出一个合适的椭圆轨迹,满足所有通过相交得到的声源两点A2、A3与阵元S的∠A2SA3在80°～100°内。综上,选取的声源点A1、A2、A3,以阵元点S为坐标元点的坐标系是较理想的。故而利用这种方法寻找的声源点A1、A2、A3,去解算阵元点S误差较小。

4 建模仿真

文中声基阵的深度为120m,阵元128个,阵的总长度150m,船行测量轨迹为椭圆,其长轴220m,短轴165m,满足短轴大于深度。仿真中,假定声基阵阵元在深度方向存在(-1,1)m的误差,声基阵布放时的测量数据与真实值在x方向上存在(0～5)m的误差,在y方向上存在(-10,10)m的误差,船行声源点高度上存在(-1,1)m的误差。

解算过程中需选取海水中的声速。海水的声速选取,是利用测量的水文数据,得到一系列与声源阵元点水平距离相对应的速度,方程(1)使用声速时,根据声源点到阵元的水平距离选取。时延差τi,存在测时误差约0.1ms,将该误差取随机量带入方程式中计算。图4根据左侧水文数据,绘制了右侧水平距离与声速的关系。

综上,通过选取任一声源点A1,利用该声源与阵元连线的垂直面与椭圆相交,得到合适的声源点A2,A3,满足解算误差较小,由于椭圆轨迹的合理选取,使得相交两点成为可能,故利用A1,A2,A3解算的同一阵元点由很多组,对这些点求平均,即得到该阵元的解算点,计算它到真实点的距离,就可得到相应阵元的解算误差长度。图5即是绘制的解算点与真实点之间的误差长度,图中阵元数128个。

分析图5可知,与真实点偏差的距离最大在0.14m以内。

5 结语

根据球面交汇求解时误差最小的条件,以声基阵原始数据为参考,航行测量椭圆轨迹满足短轴大于声基阵深度,选取椭圆航行轨迹上任一个录取点A1,求出以A1与声基阵原始点S1的连线为法线并经过S1的平面方程,平面与椭圆轨迹方程交两点a2、a3,找出与这两点距离最近的两个录取点A2、A3,即可认为A1、A2、A3这组点解算误差小。最后通过仿真计算,说明了这种方法寻找优质解算点的可靠性。

[1] 牛嗣亮,倪明,等.基于时延估计的海底线阵阵形估计方法研究[J].声学技术,2007,26(2):296-300.

[2] 吕冰,葛辉良.海底布放阵型位置的精确测量方法[J].舰船电子工程, 2013,33(9):155-157.

[3] 刘彦琼.海底声基阵大地坐标测量[J].装备环境工程,2009,6(2):42-45.

[4] 龙小民,王维等.基于平面三元阵的水声定位误差分析[J].舰船科学技术, 2011,31(06):172-174.

[5] 隋海琛,田春和等.水下定位系统误差分析[J].水道港口,2010,31(1):69-72.

[6] 于运志,姜璐等.一种水下精确定位方法及其误差分析[J].四川兵工学报,2011,32(9):121-123.

[7] 高国青,叶湘滨等.水下声定位系统原理与误差分析[J].四川兵工学报,2010,31(6):95-98.

[8] 刘彦琼,刘雨东,等.一种基于时延的水下声基阵坐标估算方法[J].海洋技术,2008,27(3):44-46.

[9] 申志伟,李志华,等.基于声基阵的目标被动探测建模与仿真[J].舰船电子工程,2011,31(8):172-175.

[10] 于平,吴波等.长基线水声定位基阵阵形优化设计[J].舰船电子工程,2015,35(5):125-127.

A Better Point Selection Methods for Coordinate of Acoustic Array of Underwater Array

ZHANG Yongchao XU Guogui

(Uint 94,No.91388 Troops of PLA, Zhanjiang 524022)

Obtaining the precise coordinate of acoustic array, it is important for measurement and localization of subaqueous object. Using a ship for measuring the coordinate of acoustic array in some assured positions, the track of ship is a ellipse. Choosing three positions, it can use spherical intersecting for calculating the coordinate of acoustic array. But the calculating error is bigger. It can get a plane which have the normal through the point in the ellipse-track and a point when the Acoustic Array located in the first instance. It has two points when the plane intersecting with ellipse, and it can use the points finding another two point by calculating their minimum distance. So the three points are needed.

acoustic array, spherical intersecting, positioning error, point selection methods

2016年10月4日,

2016年11月27日

张永超,男,硕士,助理工程师,研究方向:电磁场与微波技术。徐国贵,男,硕士,工程师,研究方向:水声通信。

TB566

10.3969/j.issn.1672-9730.2017.04.010