码辅助迭代载波同步算法的实现*
杨光辉 张曙霞 蒋宇中
(海军工程大学电子工程学院 武汉 430033)
码辅助迭代载波同步算法的实现*
杨光辉 张曙霞 蒋宇中
(海军工程大学电子工程学院 武汉 430033)
在低信噪比条件下,载波频偏和相偏会对LDPC编译码系统有明显的影响,需要接收端在译码前对频偏和相偏进行估计。为了解决上述问题,结合LDPC迭代译码输出软信息的统计特性,提出了一种适合于LDPC码的码辅助迭代载波同步技术。其基本思想是利用译码器输出的软信息辅助同步参数的估计,即将译码软信息分别用到基于代价函数的载波粗同步和基于最大似然迭代的载波细同步中,将同步器、解调器与译码器联合迭代,实现较好的载波同步。
LDPC码; 码辅助; 译码软信息; 迭代载波同步
Class Number TN911.23
1 引言
低密度奇偶校验(LDPC)码因在低信噪比(SNR)下具有接近香农限的优势,成为近期研究的热点[1]。但是,LDPC编码系统对符号同步、载波频率和相位的同步要求却很严格,即使存在很小的频偏和相偏也会使系统的性能恶化。因此为了充分挖掘LDPC码的性能,需要在系统接收端实现有效的载波同步。
极低信噪比条件下,传统的同步算法已经不能正常工作,译码模块和解调模块会脱节,出现无码可译的情况。因此,我们开始考虑采用与编码相结合的方法来实现载波同步,即利用迭代译码软信息辅助载波同步参数估计,获得比较精确的载波同步。针对LDPC编码系统的载波同步算法,已有不少研究。文献[2]提出一种基于译码软判决信息的联合迭代载波相位估计算法,在极低信噪比环境下性能却与理想同步有较大的差距。文献[3]研究了译码输出的外信息和载波相位偏移分布的关系,并利用外信息的加权对相位进行估计。文献[4]提出了基于译码软信息的改进的极性判决相位检测算法,在低信噪比条件下可获得较传统方法更为理想的同步性能,但是载波频偏和相偏的估计范围较小。文献[5]提出基于等间隔导频符号的最大似然载波估计方法,降低了运算的复杂度,具有较高的估计精度和较低的信噪比门限的优点,缺点是同步的范围较小。文献[6]提出一种基于译码软信息平方和最大的M2S2O载波同步算法,通过穷举搜索获得频率、相位的最佳估计值,但是该算法的计算和延时很大,实用性较差。
本文提出了一种利用迭代译码软信息辅助载波同步参数估计的算法,获得比较精确的载波同步。该算法以LDPC码字在迭代译码过程中输出码字的对数后验概率比(log a posteriori probability ratio,LAPPR)差值的均值(mean difference of posterior probability,MDPP)作为判决准则,对载波频偏和相偏进行匹配搜索,可以较为准确地估计较大频偏和相偏,并进行补偿,实现快速载波捕获。之后再利用最大似然准则估计得到残留的频偏和相偏,实现较好的载波跟踪[8]。
2 信号模型和LDPC译码
2.1 信号模型
信号采用MSK调制方式,在发送端,二进制数据流经过LDPC编码(码长N=2048,码率R=1/2,译码器的迭代次数最大值为10,人为设置频偏Δf和相差θ,并加入功率为σ2的高斯白噪声nm,信道为加性高斯白噪声(AWGN)信道,双边功率谱密度为N0/2。在接收端,接收信号为
rm=cm·ej(2πmΔfTs+φ)+nm
(1)
其中,Ts为码元周期。
本节所给出的算法和性能仿真都是基于下面的系统模型。
2.2 LDPC译码实现
系统采用LDPC编码方式,译码算法为置信传播(BP)算法。LDPC码是一种具有稀疏校验矩阵的线性分组码,采用BP算法进行迭代译码,迭代过程分为译码初始化、迭代过程和译码停止三部分[7]。下面将BP算法总结如下:
1) 译码初始化
(2)
其中pi(0)、pi(1)分别为信道传递给变量节点的初始化信息。
2) 迭代过程
第一步:校验节点消息更新:
(3)
第二步:变量节点消息更新:
(4)
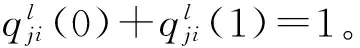
第三步:译码判决:
(5)

3) 译码停止
若HcT=0或者迭代次数达到最大值,则迭代过程结束。
3 非理想载波同步对系统的影响
在低信噪比下,从图2中可以看出载波频偏和相差对系统性能的影响。
上图为不同载波频偏和相偏条件下,系统在不同的信噪比下的平均误比特率。仿真中,码长为2048,码率为1/2,随机构造方式的LDPC码,最大译码次数为10,采用MSK调制方式[9]。
4 基于LDPC译码的迭代载波同步算法
载波同步又分为粗同步和细同步,粗同步基于相应的代价函数,其实现框图如图3。

(6)
式中,r为MSK码元的数目,对数后验概率最为译码可靠性的判决指标,绝对值越大,表示判决的结果越可靠,在迭代译码中其也会不断的迭代更新,并且会用到之后的载波细同步中,随解调器、译码器和载波同步器的迭代更新。
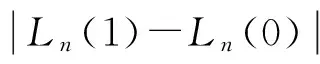
(7)
图4是测试频偏为1.1×(10-3÷8),测试相偏为1.9×(2π÷4)时的搜索估计。通过图4可以看出当m=1,n=2时MDPP取最大值,这对我们设定的测试频偏和相偏有了很好的估计。
结合LDPC迭代译码输出的软信息对接收信号r(m)进行频偏和相差的粗估计,利用粗估计得到的参数值对信号r(m)进行初步修正,载波粗同步之后得到的信号记为rcoarse。初步修正后,得到的信号还有残留频偏和相差,需要进一步修正,表达式为
(8)
细同步是基于最大似然准则,其实现框图如图5。
利用粗同步初步修正后得到的信号rcoarse,再次进行LDPC迭代译码,将输出的软信息反馈给同步器,进行载波频偏校正和载波相位校正,并进行下一次的译码迭代,这样伴随着迭代的进行,译码输出的软信息在译码器和同步器不断交互,直到两者趋于收敛,完成码辅助载波细同步的过程。
由文献[7]的推导结果可知,载波相位的对数似然函数可表示为
(9)
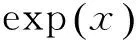
(10)
(11)
设一个MSK码元为[a(m),b(m)],其后验概率为
(12)
由式(6)和式(12)可知:
(13)
将式(12)和式(13)带入到αm的表达式中,可以推导出
(14)
将其带入相偏的最大似然估计式,即可迭代估计出相偏值。
5 系统性能分析
图6、图7给出了相位估计和归一化频率的均方误差曲线,同时给出克拉美罗限(modified Cramer-Rao bounds,MCRB)的均方误差曲线。
由图6、图7可知,本文提出的码辅助载波同步算法大幅降低相位估计、频率估计的误差,当Eb/N0≥1dB时,估计性能接近理想的MCRB,载波精度比较好,达到了预期目标。
6 结语
本文提出了一种适用于较低SNR下的基于LDPC译码软信息的迭代载波恢复算法。该算法以LDPC码字在迭代译码过程中输出码字的对数后验概率比(LAPPR)差值的均值(MDPP)作为判决准则,对载波频偏和相偏进行匹配搜索,可以较为准确地估计较大频偏和相偏,并进行补偿,实现快速载波捕获。之后再利用最大似然准则估计得到残留的频偏和相偏,实现较好的载波跟踪,其估计性能接近理想的MCRB,具有较好的载波精度。
[1] 袁东风,张海刚.LDPC码理论与应用[M].北京:北京人民邮电出版社,2008.
[2] N.Noels, C.Herzet. Turbo synchronizatio:an EM algorithm interpretation[J]. IEEE International Conference Communication.May 2003,4(11-15):2933-2937.
[3] Oh W and Cheun K.Joint decoding and carrier phase recovery algorithm for turbo codes[J]. IEEE Communication Letters,2001,5(9):375-377.
[4] 张忠培,高中杰,徐俊辉.高阶调制码辅助同步算法研究[J].电子科技大学学报,2011,40(6):825-828.
[5] 朱勇刚,姚富强,柳永祥,等.一种适用于低信噪比的ML载波频偏估计方法[J].系统工程与电子技术,2011,33(2):427-431.
[6] Freedam A,Rahamim Y. Maximum-mean-squaresoft-output(M2S2O): a method for carrier synchronization of short burst Turbo coded signals.[J]. IEEE Proc.Communication,2006,152(2):245-255.
[7] Lottici V, Luise M. Embedding carrier phase recovery into iterative decoding of Turbo coded linear modulations[J]. IEEE Trans. On Communications,2004,52(4):661-669.
[8] 潘小飞,刘爱军,张邦宁.一种新的基于最大似然估计的迭代定时恢复算法[J].信号处理,2008,24(6):957-959.
[9] 李炜,赵旦峰,钱晋希.MSK系统中迭代相位同步补偿算法[J].哈尔滨商业大学学报,2011,27(4):602-608.
[10] 沈海鸥,王永民,许华,等.基于最大化搜索的迭代载波同步算法[J].华东理工大学学报,2014,40(2):230-234.
Code-aided Iteration Carrier Synchronization Algorithm
YANG Guanghui ZHANG Shuxia JIANG Yuzhong
(College of Electronic Engineering, Naval University of Engineering, Wuhan 430033)
At low signal-to-noise ratio, the carrier frequency offset and phase offset will have a significant impact on the LDPC code system, requiring the receiver to estimate the frequency offset and phase offset before decoding. In order to solve the above problems, a code-aided iterative carrier estimation is proposed based on statistics of soft information from LDPC iterative decoder. The basic idea is to use the soft information output by the decoder to assist the estimation of the synchronization parameters, which is to use the soft information for the coarse synchronization of the carrier based on the cost function and the carrier synchronization based on the maximum likelihood iteration respectively. The better carrier synchronization is achieved by conducting the joint iteration of synchronizer, demodulator and decoder.
LDPC Codes, code-aided, soft decoding information, iterative carrier synchronization
2016年10月7日,
2016年11月26日
杨光辉,男,硕士研究生,研究方向:通信信号处理。张曙霞,女,副教授,研究方向:通信信号处理。蒋宇中,男,教授,研究方向:通信信号处理。
TN911.23
10.3969/j.issn.1672-9730.2017.04.008

