主动声纳侦察中的LFM信号参数估计方法*

金凤来 马梦博 田 振

(1.海军装备部驻天津地区防救军事代表室 天津 300042) (2.海军工程大学海军水声技术研究所 武汉 430033)

主动声纳侦察中的LFM信号参数估计方法*

金凤来1马梦博2田 振2

(1.海军装备部驻天津地区防救军事代表室 天津 300042) (2.海军工程大学海军水声技术研究所 武汉 430033)

针对主动声纳侦察中LFM信号的参数估计问题,提出一种快速有效的LFM信号参数估计方法。该方法依据LFM信号的频谱特征,通过构造频域正负门,有效解决了低信噪比情形下LFM信号中心频率估计问题；通过粗搜索和精搜索,在保证调频斜率估计精度的基础上,大大提高了运算效率；利用高精度的调频斜率估计值构造参考函数,对去载频后的LFM信号进行脉冲压缩,通过测量脉压后信号-4dB处时间宽度并取其倒数,有效解决了低信噪比情形下信号带宽估计问题。仿真结果表明了所提方法的有效性。

LFM信号; 调频斜率; 主动声纳

Class Number TN911

1 引言

二战以后,西方国家全方位配置反舰、反潜兵力,设置以主动声纳为核心的水下声探测体系。在空中,布有携带吊放声纳、声纳浮标的反潜飞机；在海上,配有携带声纳的反潜水面舰艇；在海中,配有携带声纳的反舰潜艇；在海底,布设固定式声纳探舰/潜系统,形成了空中、海上、海中、海底四位一体的立体式探舰/潜声探测体系[1]。为提高我方舰/潜艇的反侦察以及电子对抗能力,有必要对敌方发射的主动声纳信号进行研究。

线性调频(Linear Frequency Modulation, LFM)信号是主动声纳使用最为广泛的发射信号形式之一,其主要参数包括中心频率、调频斜率、带宽和脉宽。传统LFM信号参数估计方法完全从信号的性质出发,仅适用于高信噪比情形,信噪比较低时,估计精度严重下降[2～3]。本文在分析主动声纳侦察中我方被动声纳接收到的敌方主动声纳信号特征的基础上,建立信号模型,构造含噪LFM信号。在简要分析传统估计方法之后,针对其难以适用于低信噪比情形的问题,提出一种新的参数估计方法。并利用计算机仿真,分析了本文估计方法的有效性,以及相对于传统估计算法的优势。

2 信号模型

我们知道,中心频率为fc,调频斜率为μ,脉宽为T的线性调频信号可以表示为

(1)

式中A为信号幅度,rect(·)为门函数,其表达式为

依据LFM信号的性质可知,信号带宽B=μT。LFM信号是典型的大时宽带宽积信号,可以通过脉冲压缩提高信噪比,获得更高的时间分辨率。依据脉冲压缩理论,LFM信号脉冲压缩后的时间分辨率为1/B,对应于脉冲压缩后信号的-4dB时间宽度。

2.2 名义信噪比

对于我方被动声纳接收到的敌方主动声纳信号而言,信号功率Ps与噪声功率谱密度N0/2之间的比值是固定不变的,与敌方主动声纳信号的信号形式以及我方被动声纳的采样参数均无关。将该比值用SNRnorm表示,即

在一些标题的翻译中，译者还别出心裁地从目的语出发，重新创造标题，这些标题常常是原文中心思想的高度概括或是原文主要内容的别样显示。这样的例子很多，比如：

(2)

为便于表述,这里将SNRnorm定义为名义信噪比。若无特殊说明,后文统一简称为信噪比。

2.3 复高斯白噪声的产生

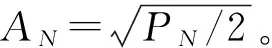
2.4 含噪LFM信号的产生

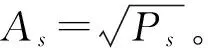
(3)

对于被动声纳接收机接收到的敌方主动声纳信号而言,其背景高斯白噪声一般为加性噪声。结合式(3)以及2.3节表述,含噪LFM信号的表达式为s2(t)=s1(t)+n(t)。

3 参数估计

3.1 传统估计方法

传统估计方法对于中心频率和带宽的估计从LFM信号的性质出发[4～7],其主要步骤包括：

上述中心频率和带宽估计方法仅适用于高信噪比情形。当信噪比较低时,S2(f)中包含的LFM信号频域波形特征不明显,导致其-3dB幅值对应的瞬时频率f1、f2测量精度降低,最终导致中心频率和带宽的估计精度变差。

传统估计方法对于调频斜率的估计采用一次搜索的方式,具体步骤如下：

3.2 本文估计方法

依据上文所述,高信噪比情形下,传统估计方法的估计精度可以满足需求,然而低信噪比情形下,低估计精度的中心频率和带宽将严重影响信号调频斜率和脉宽的估计精度。本文提出一种新的估计方法,在保证估计精度的同时,有效提高了运算效率。

3.2.1 中心频率估计

依据LFM信号的性质,LFM信号的频谱近似可以看作一个门信号,该门信号关于其中心频率左右对称。依据该特征,可以设计一个频域的正负门信号,并与LFM信号的频谱作互相关操作,进而依据相关操作的结果估计中心频率[8～10]。具体步骤如下：

1) 对我方被动声纳接收到的敌方主动声纳信号进行FFT,得到频域波形,同样记为S2(f)。注意,这里频域波形的幅值用或不用dB值表示均可。2) 设计频域正负门信号,记为SG(f)。由于并无LFM信号带宽的先验知识,正负门信号预设频率宽度需要大于或等于收集得到的敌方主动声纳信号最大带宽。一般取为最大带宽的1.2倍。正负门信号的幅值可以任意设定。如图1所示。 3) 将正负门信号SG(f)与敌方主动声纳频域信号S2(f)作互相关操作。

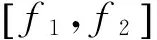
3.2.2 调频斜率估计

本文对于LFM信号调频斜率的估计采用二次搜索的方式,即将调频斜率估计值的搜索过程细分为粗搜索和精搜索两个过程。粗搜索的目的是粗略界定调频斜率的大致范围。精搜索的目的是在该范围内获取最接近待估调频斜率的精确估计值。显然,该方法既有效保证了估计精度,又大大降低了运算量。

粗搜索和精搜索的具体实现步骤与传统调频斜率估计方法基本相同。需要注意的是,粗搜索过程搜索步长较大,一般在整数级；精搜索过程搜索步长较小,一般在小数级(通常为10-1量级,如果需要更高的估计精度,可以设定为10-2量级或更高量级,但这将以牺牲运算速度为代价)。

3.2.3 带宽和脉宽估计

2.1节已述,LFM信号是典型的大时宽带宽积信号,依据脉冲压缩理论,LFM信号脉冲压缩后的时间分辨率为1/B,对应于脉冲压缩后信号的-4dB时间宽度。依据该理论,可以通过LFM信号的时间分辨率,估计信号带宽。

4 仿真分析

为验证上文所述理论的有效性,本节进行仿真分析,仿真参数如表1所示。表1中设置两种参数,区别在于信噪比的取值不同。显然,序号1为高信噪比情形,序号2为低信噪比情形。

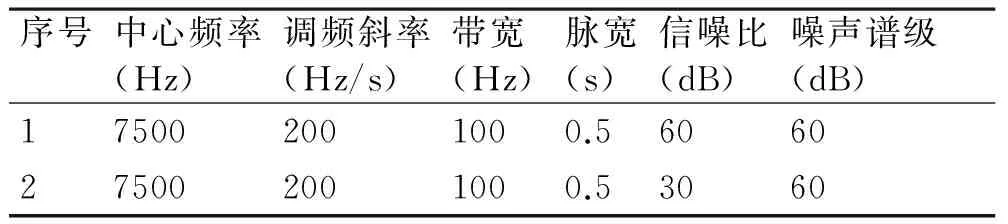
表1 仿真参数

图2和图3分别绘制了信噪比为60dB和30dB时含噪LFM信号的频谱。如图2所示,当信噪比为60dB时,信号频谱特征基本不受噪声影响,此时可以利用传统估计方法估计信号参数。当信噪比为30dB时,虽然可以大致判断信号频谱所在的频率范围,但是其特征受到噪声的严重影响,如果仍利用传统估计方法估计信号参数,可能产生较大误差,如图3所示。

仿真过程中采用蒙特卡洛方法,对传统估计方法和本文估计方法的估计结果进行分析比较。表2绘制了信噪比为60dB时信号参数估计结果,从表2可以看出,传统估计方法的估计误差与真实值的比值分别为3.07×10-5、2.7×10-3、2.2×10-2、3.2×10-2；而本文估计方法的估计误差与真实值的比值分别为0、1.35×10-4、1.38×10-2、1.4×10-2。从数值上看,两种估计方法的估计误差与真实值的比值均在10-2量级,基本能够满足实际需求。本文估计方法的估计精度略优于传统估计方法。

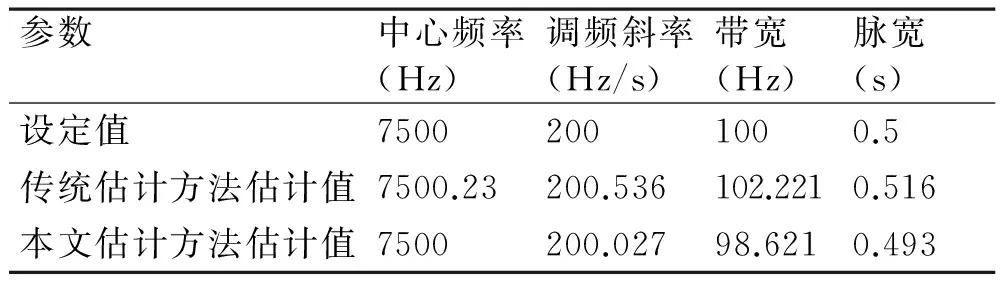
表2 信噪比为60dB时信号参数估计结果

表3绘制了信噪比为30dB时信号参数估计结果。从表3可以看出,当信噪比下降时,两种估计方法的估计精度均有下降。相比之下,传统估计方法的估计精度下降较多,其估计误差与真实值的比值分别为4.4×10-3、8.81×10-2、0.1625、0.248；而本文估计方法的估计误差与真实值的比值仅分别为1.33×10-5、3×10-3、5.21×10-2、5.4×10-2。显然,本文估计方法的估计精度要远远优于传统估计方法,在该信噪比条件下,估计精度仍能满足实际需求。

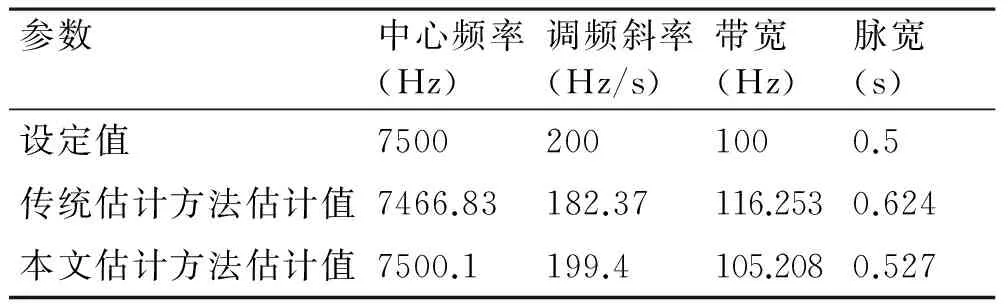
表3 信噪比为30dB时信号参数估计结果

5 结语

传统LFM信号参数估计方法仅适用于高信噪比的情形,当信噪比较低时,估计精度严重下降,估计效率较低。本文提出一种有效的LFM信号参数估计方法,有效解决了低信噪比情形下LFM信号的参数估计问题,能够在保证估计精度的基础上,大大提高估计效率,可以满足主动声纳侦察中LFM信号的参数估计需要。

[1] 唐劲松,汤子跃.电子探测原理[M].北京:电子工业出版社,2013:235-273.

[2] 王波.LFM信号检测与参数估计技术研究[D].成都:电子科技大学,2004

[3] 李洁群.超宽带LFM信号检测和参数估计方法研究[D].成都:电子科技大学,2005

[4] Xue mei, Ouyang.Short-Time Fourier Transform Receiver for Nonstationary Interference Excision in Direct Sequence Spread Spectrum Communications[J]. IEEE Trans.Signal Processing,1997,49(4),851-863.

[5] Lütfiye Durak.Short-Time Fourier Transform:Two Fundamental Properties and an Optimal Implementation[J]. IEEE Trans.Signal Processing,1999,51(5),1231-1242.

[6] H.K.Kwok and D.L.Jones.Improved instantaneous frequency estimation using an adaptive short-time Fourier transform[J]. IEEE Trans.on Signal Processing,2000,48(5),2964-2972.

[7] K.J.R.Liu.Novel parallel architecture for short-time Fourier transform[J]. IEEE Trans.Circuits Syst. 1993,40(4),786-789.

[8] 刘渝.快速解线调技术[J].数据采集与处理,1999,14(2):175-178.

[9] Peleg S, Porat B. Linear FMSignal Parameter Estimation Form Discrete-Time Observations[J]. IEEE Trans. on AES,1991,27(4):607-615.

[10] 张贤达,保铮.非平稳信号分析与处理[M].北京:国防工业出版社,1998.

Parameters Estimation Method of LFM Signal in Active Sonar Reconnaissance

JIN Fenglai1MA Mengbo2TIAN Zhen2

(1. Military Representative Office of Navy Equipment Department of Salvage in Tianjin Area, Tianjin 300042) (2. Naval Institute of Underwater Acoustic Technology, Naval University of Engineering, Wuhan 430033)

In order to resolve the problem of parameters estimation of linear frequency modulation (LFM) signals, an effective parameters estimation method is proposed in this paper. By constructing a positive-negative-gate signal in frequency domain and according to the characteristics of LFM signal frequency spectrum, the proposed method obtains a high quality of center frequency estimated value. By dividing the once search into secondary search in the estimation of chirp rate, referred as to the coarse search and the fine search, the proposed method has a high calculation efficiency and a precise chirp rate estimated value at the same time. In addition, by measuring the -4dB time width of the pulse compressed signal and taking its reciprocal, a precise signal bandwidth estimated value is obtained. The simulation results show the effectiveness of the proposed method.

LFM signal, chirp constant, active sonar

2016年10月6日,

2016年11月28日

国家“863”计划(编号：2014AA093405)资助。

金凤来,男,硕士,研究方向:航海保障技术。

TN911

10.3969/j.issn.1672-9730.2017.04.028