单桩基础动力响应性状的数值模拟分析

陈三姗 陈峰

(福建江夏学院 福建福州 350108)

单桩基础动力响应性状的数值模拟分析

陈三姗 陈峰

(福建江夏学院 福建福州 350108)

针对受到不同动荷载特性下的水平受力桩，利用PLAXIS有限元软件建立相应的数值模型，通过变动参数法分析了各个荷载条件下单桩基础的力学响应性状，进而对这些响应结果进行了深层次的机理分析。研究结果表明，随着荷载幅度的提高和循环次数的增大，桩基础的水平承载性能有所降低。而荷载频率的适当增高，有助于提高桩基础的水平承载性能。

水平荷载；单桩基础；数值模拟；承载力

0 引言

影响水平动力桩工作性能的因素很多，近年来也颇有学者对桩基础的动力响应开始关注，但相对于静荷载，动荷载下的理论研究还尚不成熟[1-5]。桩基础在静荷载和动荷载下的力学性状差异很大，其中荷载条件是影响水平受力桩发挥承载力的显著因素。

桩基础受到水平动力荷载的来源主要可分为4类：第一类主要是桩基础在海洋平台中所承受的波浪荷载，这类荷载具有频率低、加载时间短和荷载幅值大等特点；第二类是车辆行驶传递的交通荷载，这类荷载加载时间短，重复次数多，荷载幅值较小；第三类是风荷载，这类荷载具有长期性的，加载周期长等特点；最后一类是地震荷载，具有频率高、幅度大等特点。总的来说，荷载特性的不同主要是循环周期或循环频率、荷载幅度、荷载持续时间等方面的差异。根据这些不同的荷载特性，开展了水平受力桩基础的动力响应性状研究。

1 模型建立与参数选择

1.1 有限元模型建立

严格来说，建立单桩模型时用轴对称模型似乎更能符合实际情况，但也有缺点，即实体单元的自由度只有线位移，没有转角。本文主要分析的是力学性状，要求计算出剪力和弯矩，因此角位移无法忽视，故最终选择板单元。设圆型桩长度为18m，桩直径为1m，弹性模量为3×104MPa，根据圆型桩的抗弯刚度和轴向刚度，数值分析软件自动换算为板厚0.866m的单位板桩进行计算(即0.866m×1m)。单桩的其余物理参数如表1所示，有限元模型如图1所示。

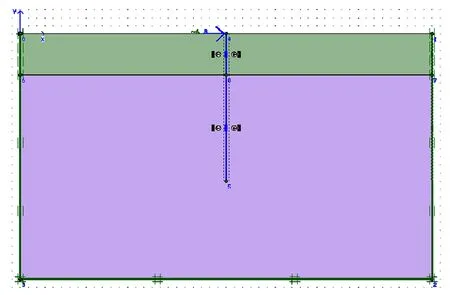
图1 单桩有限元模型示意图

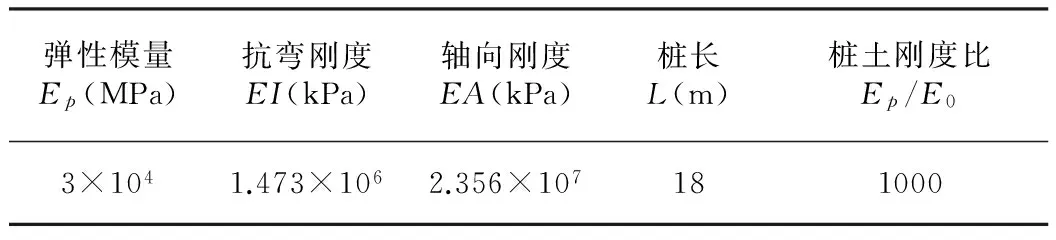
弹性模量Ep(MPa)抗弯刚度EI(kPa)轴向刚度EA(kPa)桩长L(m)桩土刚度比Ep/E03×1041.473×1062.356×107181000

1.2 土层参数与本构模型选择

表2 土体强度参数取值

小应变硬化模型(即HSS本构模型)是在硬化模型(即HS模型)上的基础上提出来的，与之相比，该模型既考虑了土体的受荷历史，又考虑了刚度的应变相关性，而本文分析为动力分析，故选用小应变硬化模型即HSS本构模型具有适用性，文献[6]详细介绍了如何应用勘察报告进行HSS本构模型参数的确定，如表3所示。

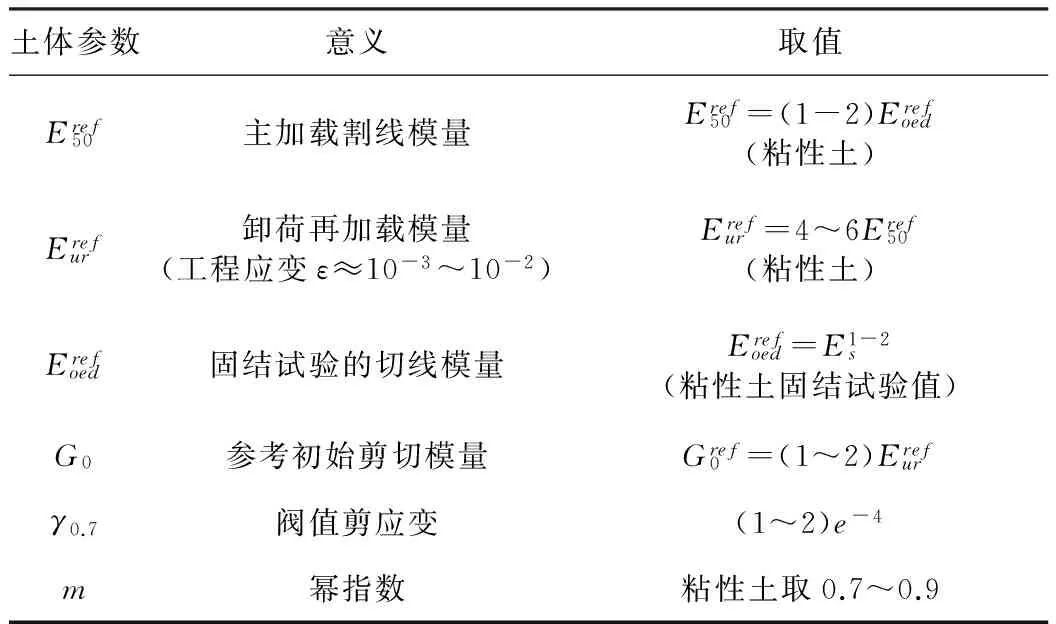
表3 HSS本构模型的参数、参数意义和取值方法

根据表3所列出的方法，模型中各动模量参数取值如表4所示。本模型中选择的土层条件为单一均匀土层，与实际复杂情况相比简单很多，故研究结果只能针对某一类土层，具有一定的限制性。

表4 HSS本构模型取值

1.3 荷载特性与参数选择

水平动力荷载的不同特性具体表现为：①荷载形式；②荷载幅度；③荷载频率；④循环次数。在本模型中，所施加的循环水平荷载是形式为有规律性的双向简谐荷载，其表达式为：

F(t)=Fsin(ωt+φ)

(1)

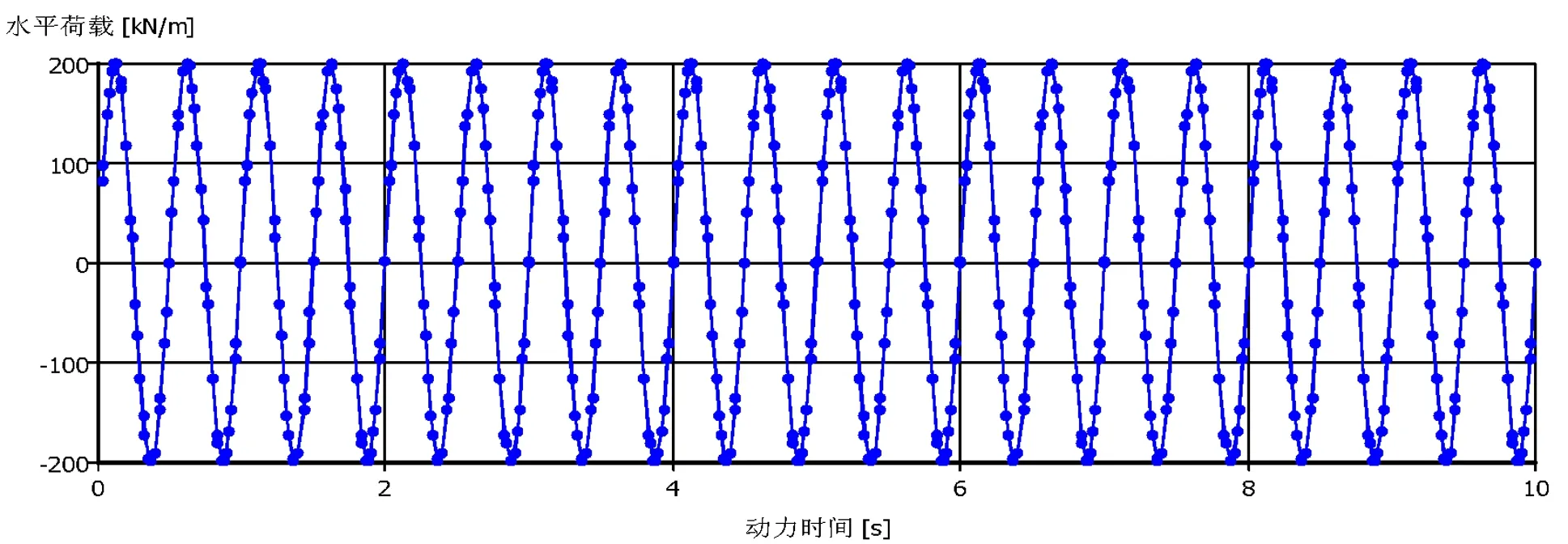
图2 双向简谐波荷载示意图

这里F为振幅，ω为荷载频率，t为荷载持续时间。初始相位角取值为0，荷载波形如图2所示。荷载幅值为变动参数时，分别取为150kN、200kN、250kN；荷载频率为变动参数时，改变荷载频率分别为0.5Hz、1Hz、2Hz；循环次数为变动参数时，改变加荷时间分别为10s、20s、30s，即循环次数分别为20次、40次、60次。

2 数值结果分析

2.1 不同荷载幅度下的力学性状

所谓荷载幅度，是指动力荷载能够达到的最大值。为了讨论荷载幅度对桩基的内力性状影响，选择频率ω为2Hz，加荷时间t=10s，循环次数=20次，幅值F=150kN、200kN、250kN，把各参数输入模型中进行分析，进而输出t=10s时刻单桩基础的剪力图和弯矩图，分别如图3(a)、(b)、(c)和图3(a′)、(b′)、(c′)所示。

在图3(a)、(b)、(c)中的桩身剪力图中，由于此时已经停止施加外荷载，根据力的平衡，此时图中的剪力值与桩周土抗力值大致相等。由图可见，荷载幅值越大桩身剪力也随之增大，相应的桩体周围的土反力也逐渐增大。而土反力增大，说明单桩本身的残余变形也是逐渐增大的。从图3 (a′)、(b′)、(c′)桩身弯矩图中可见，桩身弯矩的变化与剪力类似，荷载幅度的逐渐增大，引起的桩身弯矩也逐渐增大。可以看到，弯矩图随着荷载幅度的变化非常显著的。

由生殖系统抗原自身免疫或同种免疫引起的不孕称之为免疫性不孕。大部分原因不明的不孕夫妻可能是免疫性不孕。目前已知的致病性抗体有抗精子抗体、抗卵巢抗体、抗子宫内膜抗体、抗人绒毛膜促性腺激素抗体、抗心磷脂抗体以及抗透明带抗体等。

从以上各图可以看出：荷载幅度对单桩基础力学性状的影响是非常敏感的。究其原因，是因为在施加动力荷载的过程中，桩周土体的应变是不断变大且累积的。在其他条件相等的情况下，随着荷载幅度增大，桩体周围土的扰动范围也不断增加，发生塑性应变的区域也逐渐增加，发生的塑性应变区域越大，土体强度自然也就降低了。而土体强度的降低，意味着土抗力变小。根据桩土之间的相互作用原理，此时桩的水平承载力自然就下降，且下降程度较为明显。

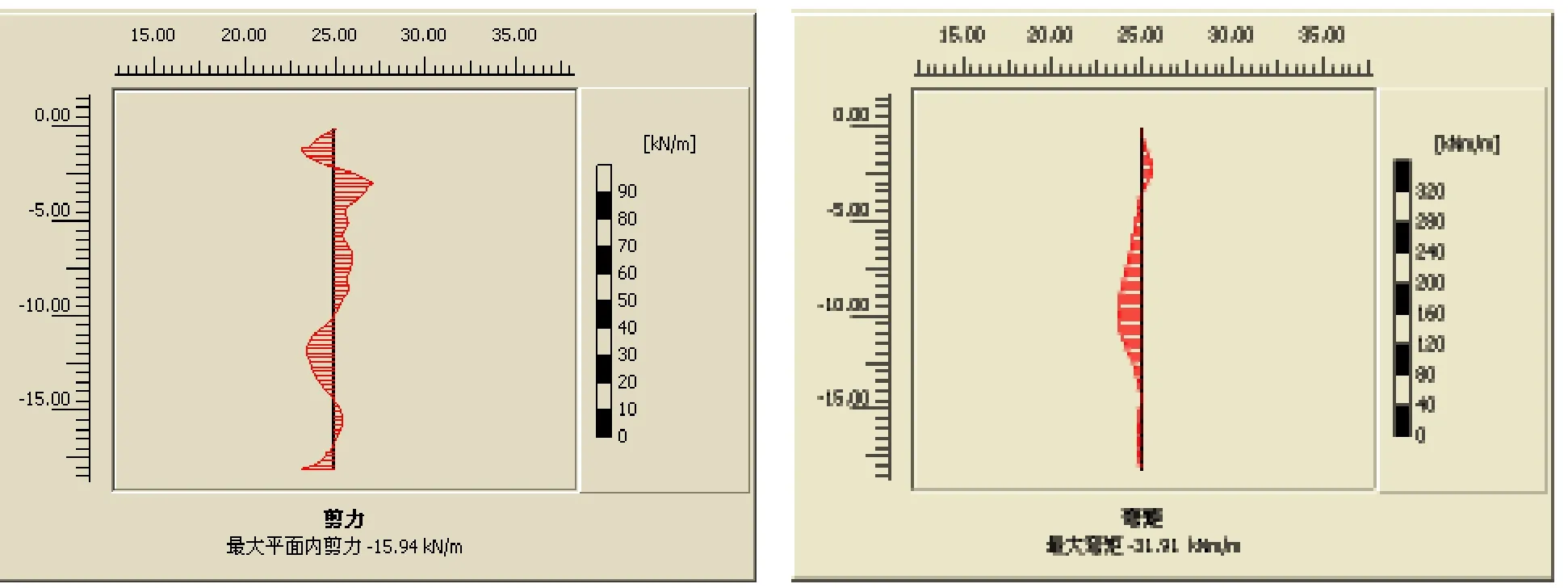
(a)F=150kN (a′)F=150kN

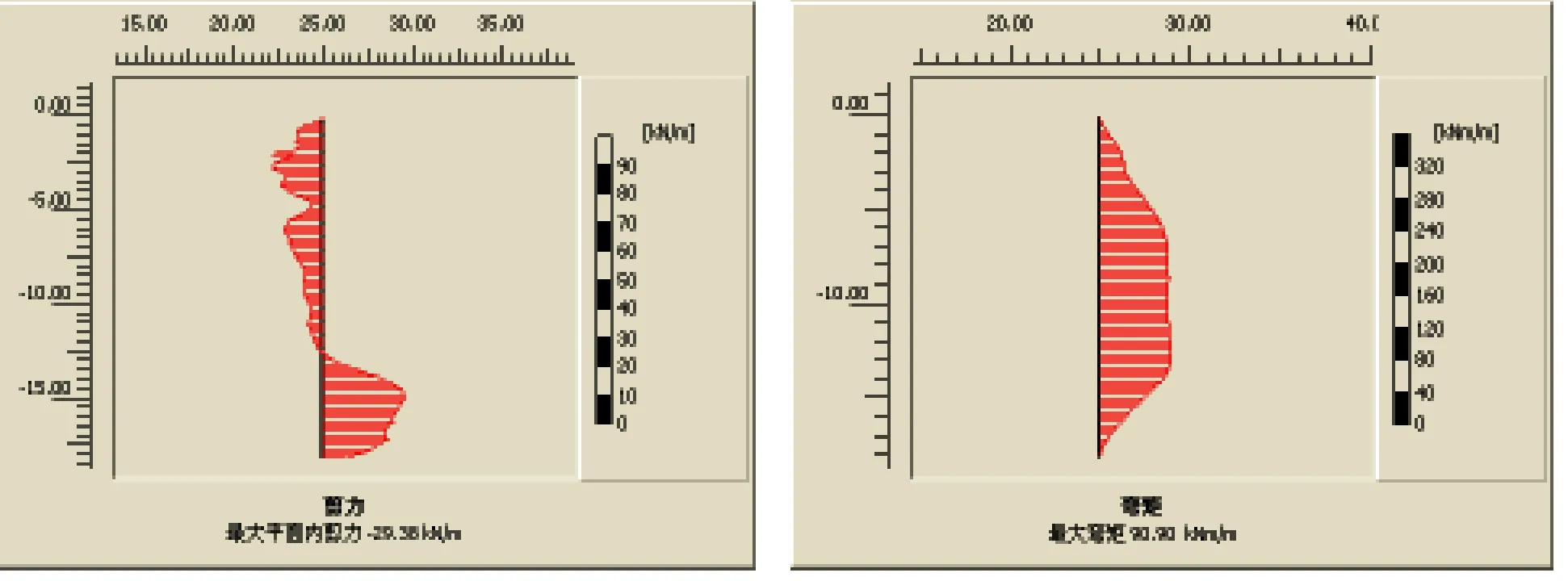
(b)F=200kN (b′)F=200kN

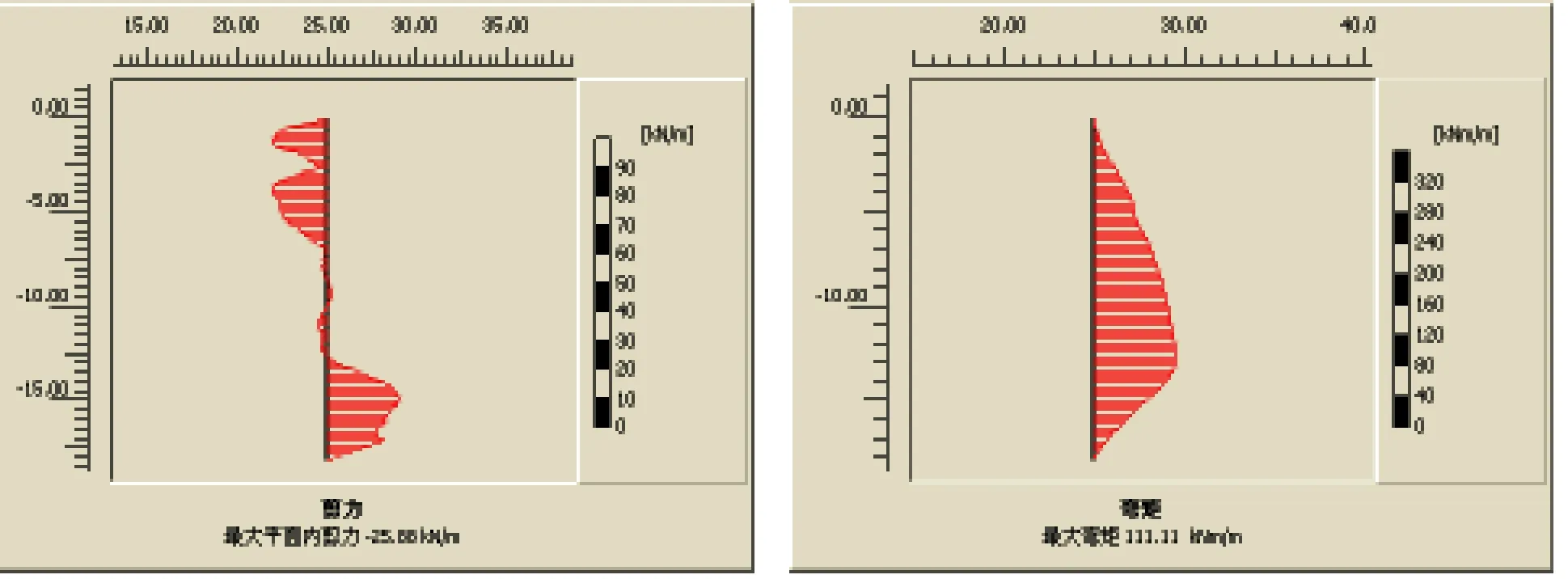
(c)F=250kN (c′)F=250kN图3 不同荷载幅度下桩身剪力图和桩身弯矩图(t=10s)(注：(a)、(b)、(c)桩身剪力图；(a′)、(b′)、(c′)为桩身弯矩图)

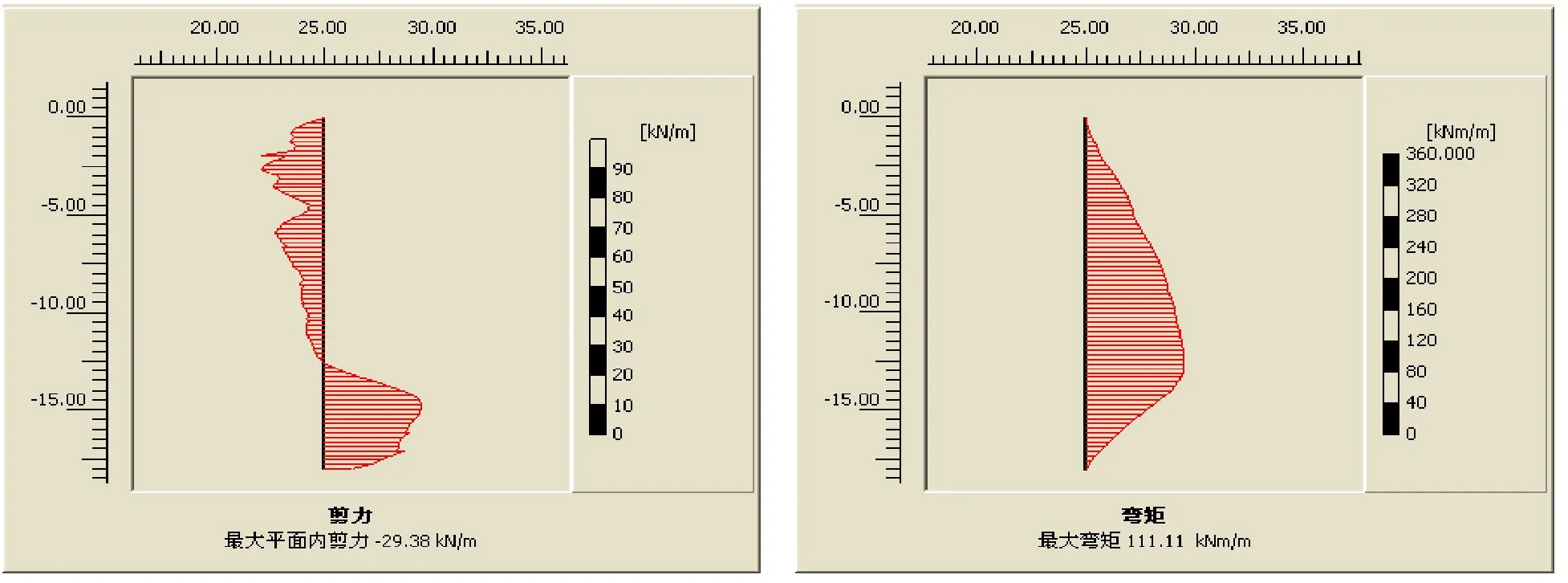
(a)ω=0.5Hz (a′)ω=0.5Hz

(b)ω=1Hz(c) (b′)ω=1Hz

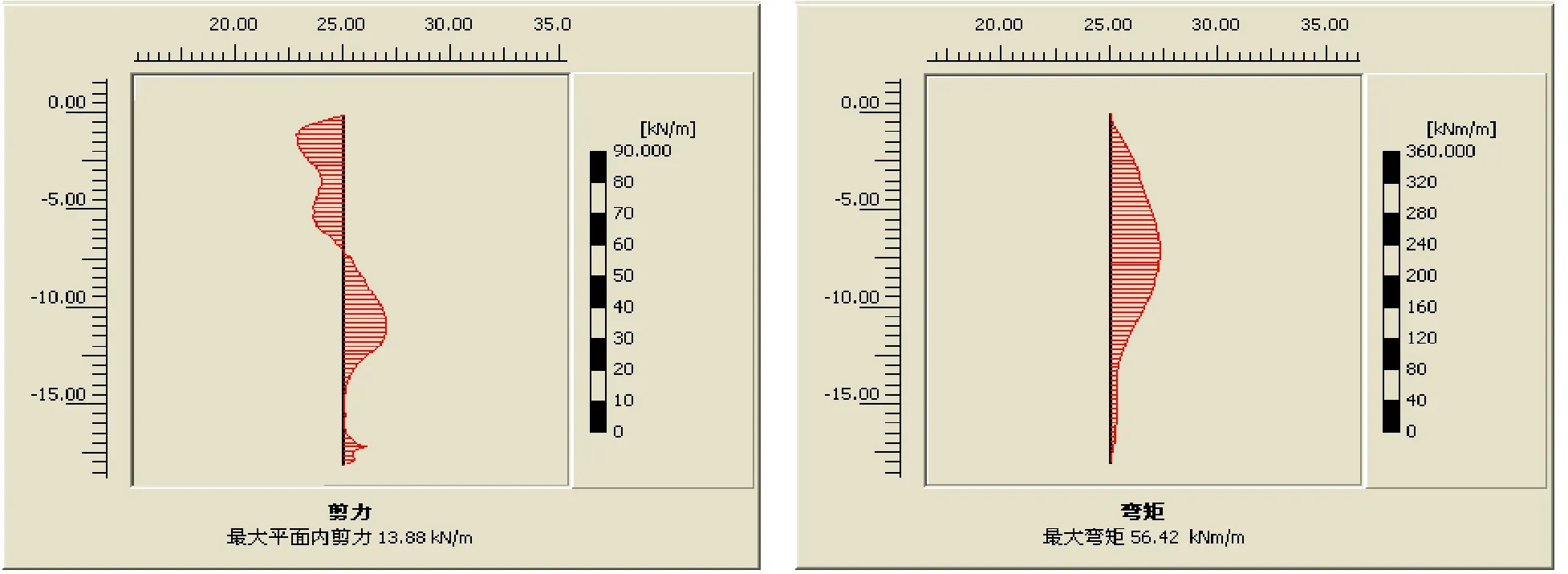
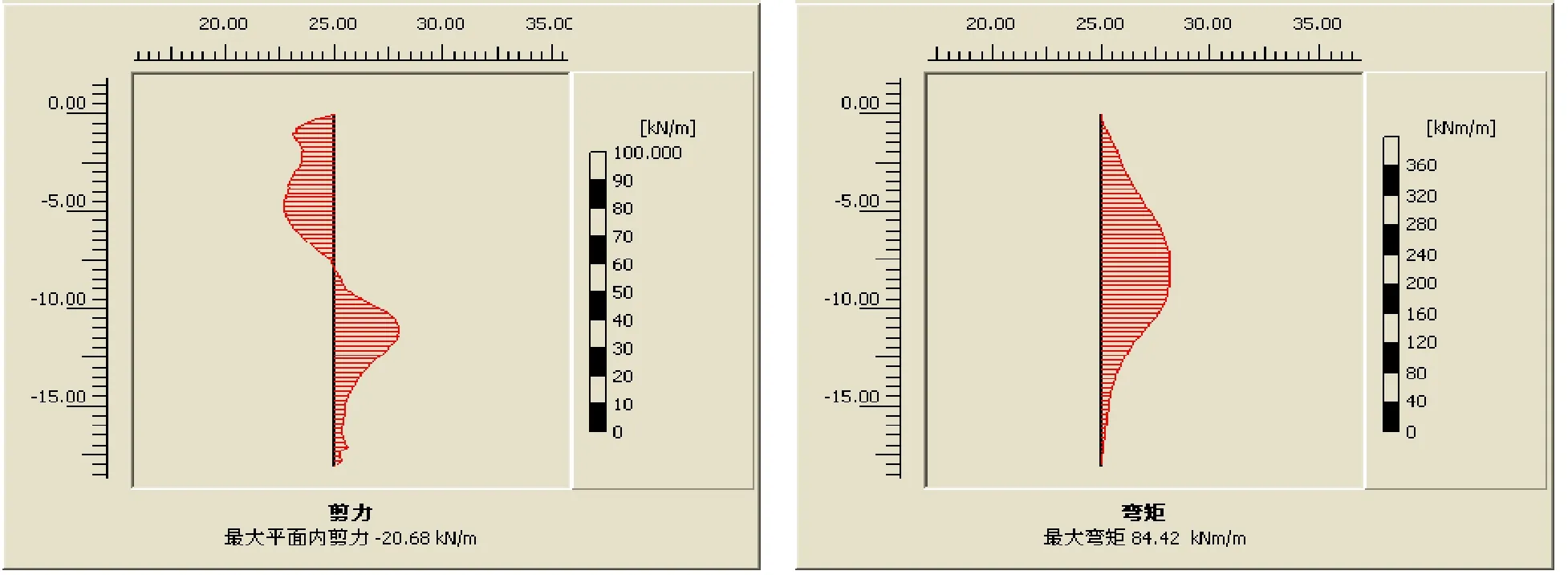
(c)ω=2Hz (c′)ω=2Hz图4 不同荷载频率下桩身剪力图和弯矩图(t=10s)(注：(a)、(b)、(c)桩身剪力图；(a′)、(b′)、(c′)为桩身弯矩图)

2.2 不同荷载频率下的力学性状

为了探讨不同荷载频率下单桩基础的水平内力情况，分别选择频率ω为0.5Hz、1Hz、2Hz。其余参数t=10s，循环次数=20次，F=200kN保持不变。所得到的的桩身剪力和桩身弯矩图分别如图4(a)、(b)、(c)和图4(a′)、(b′)、(c′)所示。

从图4(a)、(b)、(c)可以看出，剪力的最大值随着频率ω的增大而不断减小，同时剪力值为0的位置，即反向位置不断靠近桩顶。剪力值越小，说明周围土反力也越小。相应的，土抗力是随着频率的增大而增大的，而周围土体的强度增大，说明随着频率的增大，桩的承载性能也发挥得越充分。从图4(a′)、(b′)、(c′)的桩身弯矩图可以看出，桩身的最大弯矩值随着频率的增大而不断减小，且最大弯矩值的位置也不断上升。弯矩越小，说明桩身强度发挥得越少，也说明频率的适当提高，反而对桩的强度有利。

从以上现象可见，荷载频率在某一个范围内的适当增大，其实是有利于提高单桩基础及桩周土体所组成整体体系的刚度。这个结论国内外已有其他学者关注[7]，频率的适当加大能够使得桩周围土体变得密实一些，土体变得密实，又有利于提高土体强度，桩周土体强度变大，自然也就有助于提高桩的水平承载力的发挥。

2.3 不同循环次数下的力学性状

为了探讨不同的加载时间或者循环次数情况下单桩基础的内力响应，分别选择加荷时间为10s、20s、30s，即循环次数分别为20次、40次、60次。其余参数ω=2Hz，F=200kN。所得到的的桩身剪力和桩身弯矩图分别如图5(a)、(b)、(c)和图5(a′)、(b′)、(c′)所示。

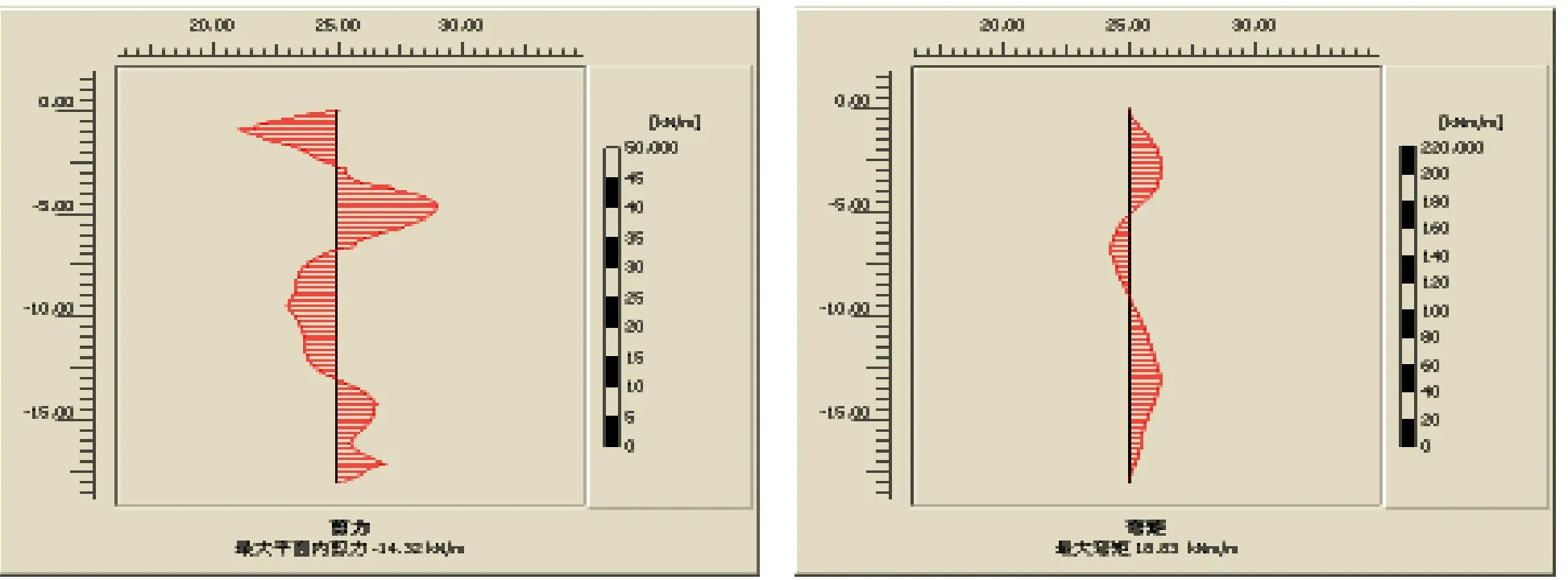
从图5(a)、(b)、(c)可以看出，桩身剪力随着循环次数的增加而不断增大，且相比图3和图4(循环20次)，明显剪力图变得更复杂。剪力的大小，侧面反映了土体残余变形的大小。剪力值越大，说明残余变形越大。事实上，循环次数的增大，

使得

(a)N=20 (a′)N=20

(b)N=40 (b′)N=40

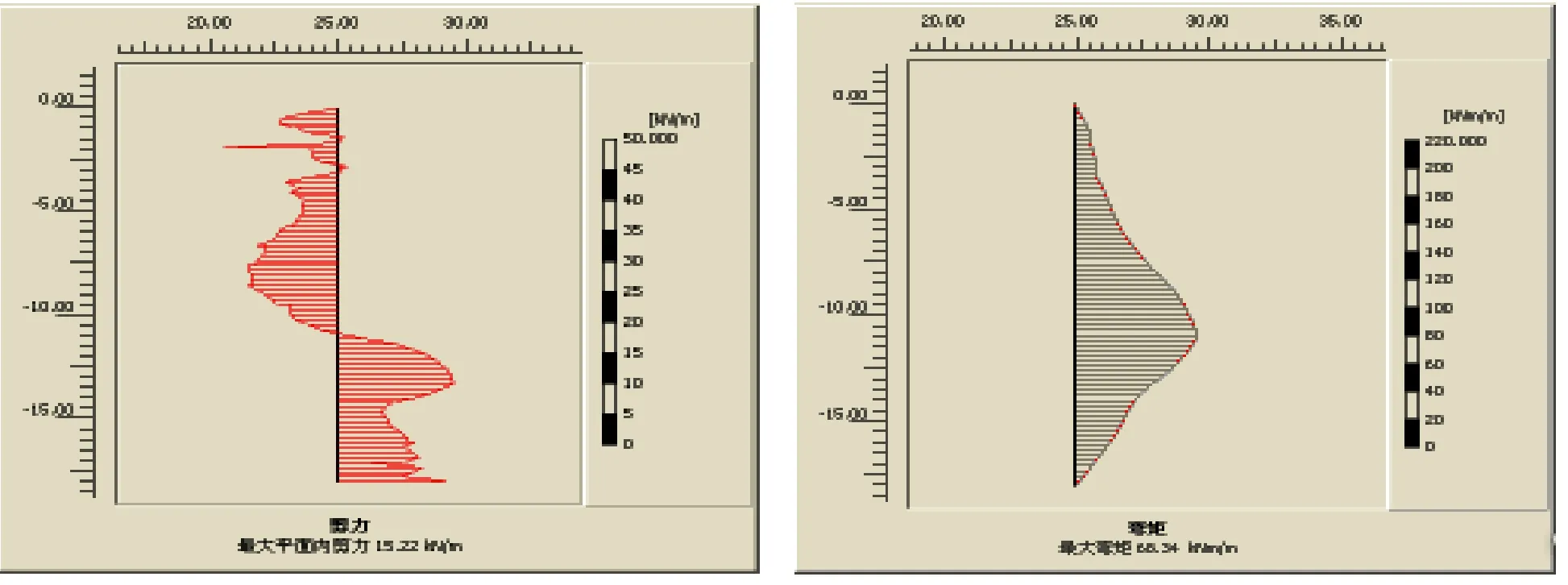
(c)N=60 (c′)N=60 图5 不同循环次数下桩身剪力图和弯矩图(t=10s)(注：(a)、(b)、(c)桩身剪力图；(a′)、(b′)、(c′)为桩身弯矩图)

单桩基础产生了疲劳变形。从图5(a′)、(b′)、(c′)桩身弯矩图可见，桩身弯矩不断增大，且弯矩图形也变得更为复杂。说明了动力循环荷载所产生的疲劳效应。

单桩的水平承载性能随着循环次数的增大而不断减小，究其原因，从桩周土的角度说，土体属于弹塑性体，在荷载的周期性作用下，其塑性应变即不可恢复变形随着循环次数的增加而不断积累，荷载反复作用的时间越长，逐渐扩大的塑性区域不断向桩身以下延伸，逐渐限制了承载力的发挥。从桩身本身角度来说，在往复作用下，桩体产生了“疲劳效应”，自身强度也慢慢下降。

3 结论

本文探讨了不同荷载幅度、荷载频率和加载时间的情况下，单桩基础的内力响应性状情况。相应的结论如下：

(1)随着荷载幅值越大，桩体的剪力和弯矩也越大，桩身强度随着幅值得增大而衰减得越快。且此时单桩周围土体发生塑性应变的区域越大，土体强度越低，越影响桩的水平承载力的发挥。

(2)适当提高荷载频率，使得单桩周围土体变得越密实，提高土体强度，有利于单桩基础水平承载性能发挥得越充分。

(3)随着循环次数的增加，桩周土体塑性应变随着循环次数的增加而不断积累，桩的水平承载力越来越低。

(4)适当加大频率有利于单桩基础水平承载性能的发挥，而循环次数的增大又使得桩基础发生“疲劳效应”。实际的桩基础，其受力和变形性状是频率和循环次数叠加的效果。在计算水平极限承载力时，需同时考虑二者的相互影响。

[1] 郭鹏飞.循环荷载作用下饱和黄土地基单桩承载特性模型试验研究[D].兰州：兰州交通大学，2013.

[2] 任宇.长期竖向循环荷载作用下桩的变形特性试验及理论研究[D].杭州：浙江大学，2013.

[3] 张晓冬.基于ABAQUS的风机单桩基础及公路路基累积位移分析[D].杭州：浙江大学，2014.

[4] 陈三姗.循环水平荷载作用下桩基础的响应性状研究[D].福州：福州大学，2014.

[5] 杨启斌.双向简谐波荷载作用下群桩的力学性状分析[J].福建工程学院学报，2015(6):526-531,536.

[6] 杨赟.小应变土体硬化模型参数对基坑数值计算的影响分析[D].天津：天津大学，2014.

[7] 李涛.近海风机导管架基础水平受荷特性研究[D].杭州：浙江大学，2015.

Numerical Simulation Analysis of Dynamic Mechanical Properties for Single Horizontal-loaded Pile

CHENSanshanCHENFeng

(Fujian Jiangxia University, Fuzhou 350108)

The response characteristics of the internal force of single pile under different load conditions was analyzed here by finite element numerical model which established by the finite element software PLAXIS.Then the mechanism of these response characteristics was carried out.The research results show that the single pile bearing performance reduced with the increase of load amplitude and cycle number.And appropriately increasing of the load frequency can help to improve the single pile bearing performance.

Horizontal load; Single pile; Numerical simulation; Bearing capacity

福建江夏学院青年科研人才培育基金项目：超塑化剂作用下粉煤灰水泥土的强度特性及固化机理研究(JXZ2016005)。

陈三姗(1988.11- )，女，助理实验师。

E-mail:sanshanchen@sina.com

2017-01-06

TU473

A

1004-6135(2017)03-0076-04