磁通门磁强计感应回路的稳态解析模型*

刘 斯,曹大平,唐立军,何兆国(.长沙理工大学物理与电子科学学院,长沙 404;.武汉大学物理科学与技术学院,武汉 4007 .哈尔滨工业大学深圳研究生院,广东 深圳 58055)



磁通门磁强计感应回路的稳态解析模型*

刘 斯1*,曹大平2,唐立军1,何兆国3
(1.长沙理工大学物理与电子科学学院,长沙 410114;2.武汉大学物理科学与技术学院,武汉 430072 3.哈尔滨工业大学深圳研究生院,广东 深圳 518055)

针对磁通门磁强计感应回路中调谐电容对灵敏度的影响,提出了磁通门感应回路的分段解析稳态模型,计算了不同调谐电容值时的感应电流波形及峰-峰值。计算与实验的对比表明,感应波形之间相关系数均大于0.98,峰-峰值p平均计算误差小于3%。调谐电容在±8%内变化时,引起的磁通门灵敏度变化为大于37%。本文提供的磁通门感应回路稳态模型能够用于精确描述输出电流性质,为研究磁通门系统的温度稳定性提供分析和参考。

磁通门;磁传感器;参数放大效应;灵敏度;稳定性

磁场测量是了解太阳系各主体行星环境信息的重要手段之一[1-2]。高精度地磁场数据对建立空间等离子体运动模型及测量高能粒子通量具有重要意义[3-5]。磁通门磁强计是目前在地球磁场及空间ELF(Extremely Low-Frequency)电磁波测量方面应用最为广泛的科学仪器,它具有可靠性高、结构简单和成本较低等特点[6-7]。用于地球磁层研究的磁通门磁强计的主要作用是测量背景磁场及在背景磁场上叠加的低频磁场波动,用于研究亚暴起始时的突变重构[8],为计算高能粒子相空间密度提供直流磁场数据,也可用于研究ELF/ULF波的激发机制,为了解EMIC等电磁波对辐射带能量粒子的动力学演化过程提供观测支持。因此,研究高灵敏度的磁通门磁强计对我国空间科学探测发展非常重要。

地球空间磁场的变化幅值相对地球主磁场而言非常小,因此对用于空间探测的磁通门磁强计灵敏度要求较高。目前通常采用在感应回路中串联或并联电容负载,通过电容与探头感应线圈谐振来提高灵敏度[9]。探头感应线圈电感随激励电流周期性变化,因此谐振频率由激励频率决定。基于Serson-Hannaford近似的参数放大理论指出[10],输出二次谐波的磁通门探头,可以通过参数放大效应将四次谐波的能量传输到二次谐波中,从而大幅改善磁通门磁力计系统的信噪比,信号增益可达50 000[11]。参数放大理论能够用于定性地解释调谐对信号放大的作用,但Serson-Hannaford近似,仅采用了感应电流的二次及四次谐波进行分析,忽略电流高次谐波会导致计算谐振电容和感应电流时产生的误差。前期工作[12]通过分析激励电路与感应回路之间的能量传递,在不对电流波形进行傅立叶分解及近似的情况下,提供了定量计算调谐参数的方法。不同的调谐电容将导致感应电流峰值的变化,从而影响探头灵敏度[13]。由于空间测量环境温度的变化会引起电路参数变化,因此定量地描述调谐电容变化对感应电流的影响能够为分析磁通门磁强计灵敏度温度稳定性提供基础[14]。Primdahl等[15-16]对感应电流输出进行了一定的分析,利用数值迭代[17]和SPICE软件[18]能够在一定程度上重复感应回路运行过程,但没有分析电路元器件变化对感应电流及磁强计输出带来的影响。

因此,本文主要在分析磁通门感应最佳能量传递条件[12]的基础上,通过对输出二次谐波的短路磁通门感应回路基本方程进行迭代求解,得到磁通门磁强计感应电流分段解析模型。进一步利用感应电流波形的稳态模型,分析磁通门输出信号的幅值与调谐电容的关系,通过与实验结果对比,验证了调谐电容变化对探头灵敏度的影响。

图1 感应电路原理图

1 感应回路微分方程

磁通门探头为一个具有磁芯的线圈,磁芯的表观磁导率随激励电流变化的,为真空磁导率,、与分别为感应线圈匝数、截面积(m2)与等效长度(m)。在感应电路中可将探头等效为随时间变化的电感L(t),电流输出磁通门感应回路等效原理如图1所示,其中C和R分别为感应电路调谐电容和电阻。设待测磁场为,表示回路电流所产生的磁场强度。

磁探头感应线圈内的磁通量:

(1)

式中:L(t)为感应线圈电感值:

(2)

令iex表示外磁场等效电流:

(3)

磁通门感应回路方程为:

(4a)

i(t)=q′t

(4b)

式中:q为电容上得电荷量,i为回路中的电流,R是总的直流电阻,包括负载电阻和线圈的直流电阻,C是电容,因此,磁通门感应回路的二阶微分方程为:

(5)

2 感应回路分段解析解

在激励磁场的作用下,由于探头磁芯交替处于饱和与非饱和状态,因此感应线圈电感L(t)可近似地采用非饱和电感LHIGH与饱和电感LLOW来描述,如图2所示。设电感值的变化周期为T,电感变化波形的占空比为η,η的值由激励电路参数决定[18]。t=0时,磁芯进入饱和状态,感应电感跳变为LLOW;t=t1时,磁芯进入非饱和状态,感应电感跳变为LHIGH。

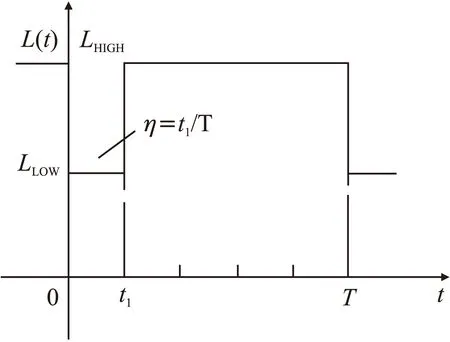
图2 感应线圈电感跳变模型

对于磁芯饱和状态,感应回路微分方程为:

(6)

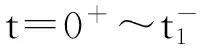
(7)

(8)

而在磁芯的非饱和状态,感应回路方程为:

(9)

处于非饱和态时,回路电流和电容电荷具有同样形式的解。由于回路中电流和电荷为有限值,所以L(t)[i(t)+iex]在跳变点两边连续,跳变点t=t1处有:

(10)

且在回路中电容上的电荷变化连续,可得到状态改变时的边界条件:

(11)

(12)

通过时的边界连续性条件,求解感应回路非饱和段方程,在跳变点时刻,可类似得到边界连续条件:

(13)

q(T+)=q(T-)

(14)

i(T+)、q(T+)将作为下一周期中磁芯饱和段的初始条件进行计算。

因此,在一个周期内,激励电流产生的磁场使磁芯饱和的区间,感应线圈电感取较小值LLOW,回路电流及电容电荷满足式(7)～式(8);在磁芯非饱和区间,感应线圈电感取值LHIGH。感应回路在两个状态之间持续转换,且感应线圈电感与调谐电容之间均能够产生谐振。在状态变化临界点,边界条件由能量守恒及电荷连续给出,通过式(11)～式(12)及式(13)～式(14)能够计算出状态变换的初始值。在电路损耗足够大的情况下,上述暂态解迭代将收敛到稳态模型。本文把用这种方法得到的稳态模型称为磁通门感应回路的稳态模型。

3 结果与讨论

实验所用磁通门探头感应参数如表1所示。探头磁芯饱和段所占比例(图2中的η)由激励参数决定,激励电流波形如图3所示,激励频率为11.718 5kHz,η约为18%。利用稳态模型进行计算时,采用实验测得的电路参数,待测磁场由通电螺线管在磁屏蔽筒内产生,静磁场约为40 000nT。

表1 磁通门探头感应参数

图3 实验中示波器采样的激励电流波形

曲线1代表激励电路中的激励电流其p-p值为390 mA;曲线2代表激励电压,其p-p值为5 V。横坐标代表时间(10 μs/格)。

本文根据所建立的感应回路稳态模型,分别对不同调谐电容的感应电流进行了计算,并与实验结果进行对比。实验装置如图4所示,激励频率为11.7 kHz,通过电容调谐以降低激励功耗。磁通门探头输出为与待测磁场幅值成正比的二次谐波,调谐后输出的感应电流通过反馈电阻值为100 Ω的电流-电压转换器,转换为电压值,并采用Tektronix TDS 1012B数字示波器获取。

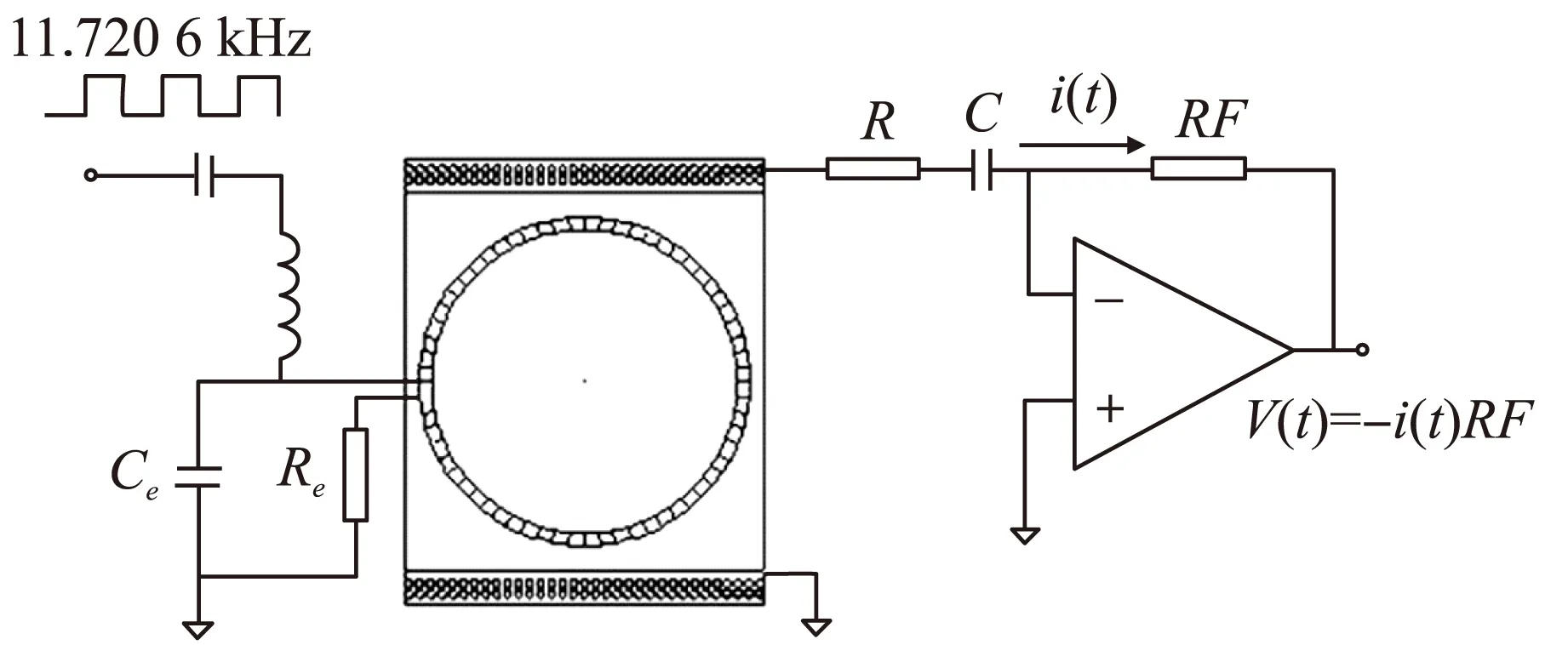
图4 感应电流波形获取实验原理图

Ce是激励电路中的并联电容,Re是激励电路的电阻;R是感应回路中的电阻,C是调谐电容,RF是放大器的反馈电阻,V(t)是放大器的输出

图5为不同调谐电容时,实验测得的感应电流波形与计算结果对比,其中虚线为实验波形,实线为计算结果:图5(a)为调谐电容为36.5 nF时,对比实测感应电流与计算结果,实验与计算的波形之间相关系数为0.991,它们的电压峰-峰值分别为2.32 V和2.35 V,误差为1.29%;图5(b)为调谐电容采用38.7 nF时的对比感应电流。实验波形与计算波形间相关系数为0.993,电压峰-峰值分别为3.06 V和3.14 V,误差为2.54%;图5(c)为调谐电容采用40.6 nF时的对比图,二者之间的相关系数为0.987,电压峰-峰分别为2.62 V和2.66 V,误差为1.50%。

图5 感应电流实验波形与计算波形

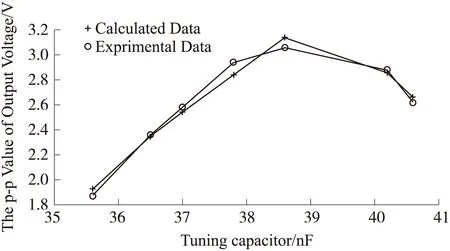
图6 不同调谐电容时的输出电流峰值变化,其中+为计算值,○为实验值

磁通门系统的输出电压是对感应电流波形积分后并进行低通滤波的直流电压,因此图4所示的开环系统输出的电流峰-峰值反映了探头调谐后的灵敏度。根据最佳能量传输条件,调谐电容过大或过小都会引起感应电流峰值降低,因为它会使磁通门饱和段与非饱和段的震荡频率偏离最大能量传输条件所需满足的相位关系,降低感应回路接收到的能量,从而引起磁通门灵敏度降低。在空间环境中,由于环境温度变化会导致调谐电容值变化,因此本文计算了在调谐电容在35 nF～41 nF范围内变化时的感应电流峰-峰值,如图6所示,其中+为计算值,○为实验值。由图5可知,在调谐电容由36.5 nF变化到40.6 nF时,输出电压在1.94 V～3.10 V内变化,即调谐电容在±8%范围内变化引起的磁通门灵敏度变化约为37.4%。

4 结论

为了进一步理解磁通门磁强计感应回路中调谐参数对灵敏度的影响,并为提高磁通门灵敏度温度稳定性提供分析数据,本文在电感跳变近似以及感应回路最佳能量传递条件的基础上,提出了磁通门感应回路的分段解析稳态模型。利用该稳态模型和实测电路数据,本文求解了3种不同调谐电容值时的感应电流波形,计算结果与实验测得的波形之间的相关系数均大于0.985,表明本文所建立的感应迭代稳态模型能够精确描述磁通门输出二次谐波电流波形,能够为磁通门的感应回路的设计和调试提供数学工具。同时,为了提供磁通门灵敏度温度稳定性的分析数据,本文进一步计算了不同调谐电容对感应电流峰-峰值的影响,计算与实验的相应变化趋势一致,误差小于3%。计算及实验结果表明调谐电容变化范围在±8%内时,引起的磁通门灵敏度变化为大于37%。因此,结合元器件筛选和器件的温度系数,本文提供的稳态模型能够用于计算磁通门工作环境温度变化对灵敏度的影响,为研究系统的温度稳定性提供分析和参考。

[1] Bartington G,Chapman C E. A high-Stability Fluxgate Magnetic Gradiometer for Shallow Geophysical Survey Applications[J]. Archaeol Prospect,2004(11):19-34.

[2] Simpson D,Lehouck A,Verdonck L,et al. Comparison between Electromagnetic Induction and Fluxgate Gradiometer Measurements on the Buried Remains of a 17th Century Castle[J]. J Appl Geophys,2009,68(2):294-300.

[3] Ness N F. The earth’s Magnetic Tail[J]. J Geophys Res,1965(70):2989-3005.

[4] Lin N,Mcpherron R L,Kivelson M G,et al. Multipoint Reconnection in the Near-Earth Magnetotail:CDAW 6 Observation of Energetic Particles and Magnetic field[J]. J Geophys Res,1991,96(11):427-439.

[5] Paschmann G,Haerendel G,Papamastorakis I,et al. Plasma and Magnetic Field Characteristics of Magnetic Flux Transfer Events[J]. J Geophys Res,1982,87(4),2159-2168.

[6] Magnes W,Diaz-Michelena M. Future Directions for Magnetic Sensors for Space Applications[J]. IEEE Trans on Magn,2009(45):4493-4498.

[7] Acuna M H. Space-Based Magnetometers[J]. Rev Sci Instrum,2002,(73):3717-3736.

[8] Auster H U,Glassmeier K H,Magnes W,et al. The THEMIS Fluxgate Magnetometer[J]. Space Sci Rev,2008(141):235-264.

[9] Ripka P,Primdahl F. Tuned Current-Output Fluxgate[J]. Sens Actuat A:Phys,2000,(82):161-166.

[10] Player M A. Parametric Amplification in Fluxgate Sensors[J]. J Phys D,1988,(21):1473-1480.

[11] Kim H C,Jun C S. A New Method for Fluxgate Magnetometers Using the Coupling Property of Odd and Even Harmonics[J]. Meas Sci Technol,1995,6(7):898-903.

[12] Cao D P,Liu S,Jiang C Z. Maximum Energy Transfer Conditions in Parameteric Amplification of Current-Output Fluxgate Sensors[J]. Sens Actuat A:Phys,2012,(173):136-140.

[13] Russell R D,Narod B B,Kollar F. Characteristics of the Capacitively Loaded Flux Gate Sensor[J]. IEEE Trans Magn,1983,19(2):126-130.

[14] 齐侃侃,石超,吕冰. 磁通门传感器探头温度特性研究[J]. 传感技术学报,2014(11):1486-1489.

[15] Primdahl F,Petersen J R,Olin C,et al. The Short-Circuit Fluxgate Output Current[J]. J Phys E:Sci Instrum,1989,(22):349-353.

[16] Primdahl F,Ripka P,Petersen J R,et al. The Short-Circuit Fluxgate Sensitivity Parameters[J]. Meas Sci Technol,1991,(2):1039-1045.

[17] Trujillo H,Cruz J,Rivero M,et al. Analysis of the Fluxgate Response through a Simple Spice Model[J]. Sens Actuat A:Phys,1999,(75):1-7.

[18] Vuillermet Y. About the Use of Numerical Integral Methods to Simulate a Fluxgate Magnetometer:The Ring-Core Example[J]. Sens Actuat A:Phys,2010(163):48-53.

[19] Cao D P,Liu S,Jiang C Z. A Solution of Fluxgate Excitation Fed by Squarewave Voltage[J]. Sens Actuat A:Phys,2010(163):118-121.

刘 斯(1984-),女,汉族,2005年毕业于武汉大学应用物理系,获学士学位,2012年获武汉大学微电子学与固体电子学专业博士学位。现任职于长沙理工大学,主要研究方向为空间磁场探测技术、地球磁层物理。

An Analytical Steady-State Model for Fluxgate Magnetometer Detector Circuit*

LIU Si1*,CAO Daping2,TANG Lijun1,HE Zhaoguo3
(1.School of Physical and Electronic Sciences,Changsha University of Science and Technology,Changsha 410114,China;2.School of physics and Technology,Wuhan University,Wuhan 430072,China;3.Shenzhen Graduate School,Harbin Institute of Technology,Shenzhen Guangdong 518055,China)

An analytical model is developed to evaluate the influence of detector tuning capacitor effects on the sensitivity of fluxgate. The waveforms and the p-p value variation of the fluxgate output current are calculated with different tuning capacitances. The corresponding experiments are performed to measure the pick-up current in a uniform magnetic field. The correlation coefficients between the calculated and the measured waveforms are higher than 0.98,and the averaged deviation of the p-p value is less than 3%. The sensitivity varies 37% with the tuning capacitance changing within ±8%. This analytical model provides a useful tool for studying the properties of output of fluxgate efficiently and directly,and it also can be utilized for fluxgate temperature stability analyzing.

fluxgate;magnetic sensor;parametric amplification;sensitivity;stability

项目来源:湖南省教育厅科研一般项目(13C1034);长沙理工大学近地空间电磁环境监测与建模湖南省普通高校重点实验室开放基金项目(201502);深圳市科技计划项目(JCYJ20160226201347750,JCYJ20160817172025986)

2016-08-03 修改日期:2016-11-30

O44

A

1004-1699(2017)04-0555-05

C:7310L;3120W

10.3969/j.issn.1004-1699.2017.04.012