基于准静止磁场检测的行人导航算法框架iIEZ+*

张立强,苏 中,李 擎(北京信息科技大学高动态导航技术北京市重点实验室,北京 100101)



基于准静止磁场检测的行人导航算法框架iIEZ+*

张立强,苏 中*,李 擎
(北京信息科技大学高动态导航技术北京市重点实验室,北京 100101)

在行人惯性导航领域,地磁修正算法作为一种有效的修正航向漂移误差的方法,应用在磁干扰环境中时,存在航向失真的问题,而航向精度往往决定了整个导航系统的优劣。为此,在Afzal提出的准静止磁场检测算法的基础上,提出了行人导航算法框架iIEZ+,即以Jiménez A R提出的IEZ+框架为基础,融入了改进后的准静止磁场检测算法,对地磁修正算法和启发式航向漂移消除算法的使用做出选择,实现了两种算法间的优势互补。实验表明,本文提出的算法框架可以有效抵御磁干扰的影响,提供可靠的航向和位置信息。经过多次室内外行走实验,定位误差约为路程的0.6%～1.6%,优于文中提到的其他基于IEZ框架的算法。

行人惯性导航;准静止磁场检测;扩展卡尔曼滤波器;地磁修正算法;启发式航向漂移消除算法;磁干扰

在行人惯性导航领域,由于MEMS惯性器件误差随时间不断累积,尤其是陀螺仪误差累积带来的航向漂移问题,制约了整个行人导航系统的发展。为了削弱误差,提高定位精度,国内外学者进行了大量研究。Foxlin[1]提出了INS(Inertial Navigation System)+EKF(ExtendedKalman Filter)+ZUPT(Zero velocity UPdaTe)框架(IEZ)对行人位置进行估计,但是没有引入外部观测量对航向误差做出修正。Rajagopal S[2]在IEZ框架的基础上融入了零角速度更新算法ZARU(Zero Angular Rate Update)对陀螺仪零偏误差进行修正。Jiménez A R等人[3]改进了IEZ框架,即融入了零角速度更新算法(ZARU)、地磁修正算法MC(Magnetic Correction)以及启发式航向漂移消除算法HDE(Heuristic DriftElimination)对陀螺仪零偏误差和航向误差做出修正,提出了IEZ+框架。文献[3]中结果表明该框架能够很好的抑制航向漂移,在磁干扰环境中具有较好的定位精度,但是IEZ+框架中的MC算法和HDE算法需要使用相同的航向角误差Δψ作为观测量,文中缺少两种算法使用先后顺序、使用时间段以及如何应对磁场干扰等问题的说明。钱伟行等人[4]沿用了IEZ框架,使用磁强计对航向进行初始对准,但是在行走过程中随着陀螺仪误差的不断积累,航向依旧会发散。张新喜等人[5]利用零速时刻该点地磁场模值恒定的特性,实现了磁强计的在线校准,提高了航向精度。本文作者张立强等人[6]将ZARU算法和MC算法融入IEZ框架,同时利用脚部在零速时刻相对于地面静止的特点,实现了加速度计对俯仰和滚转角的观测更新,从而减小了姿态解算误差,提高了定位精度,但是框架中的MC算法很容易受到其他磁场干扰的影响而导致航向失真。

磁强计经过适当的校准后,可以通过MC算法提供相对于真北方向几度误差的绝对航向[7]。虽然该算法受限于磁干扰环境,考虑到它的使用对提高航向精度有很大的帮助,并且真实的磁场环境总会存在纯净的地磁场环境。因此,本文在Jiménez A R等人提出的IEZ+框架的基础上,加入了准静止磁场检测器,针对磁场干扰情况选择性的使用MC算法或者HDE算法,提出了基于准静止磁场检测的改进型IEZ+框架iIEZ+(improved IEZ+)。该框架避免了单一依靠MC算法容易受到磁干扰影响[8]或者单一依靠启发式航向漂移消除算法在人体连续转向时容易积累陀螺仪零偏误差的问题[9],实现了两种算法间的优势互补,解决了干扰磁场中地磁航向失真的问题,提高了定位精度。

图1 iIEZ+框架结构示意图

1 iIEZ+算法框架

本文框架基于JiménezAR提出的IEZ+框架,整体结构如图1所示。它使用包含15维状态向量δx=[δφ,δωb,δr,δv,δab]T的EKF对行人的位置和姿态做出估计。该向量包含姿态误差δφ、陀螺仪零偏误差δωb、位置误差δr、速度误差δv以及加速度计零偏误差δab。

当人体行走或静止时,足部从接触地面到抬起的过程或者持续接触地面的过程被称为零速状态。此时,足部相对于地面几乎没有滑动摩擦,因此认为它的速度和角速度为零。EKF分别利用此时的零速和零角速度对速度误差δv和陀螺仪零偏误差δωb进行观测更新,即所谓的ZUPT和ZARU算法。因为此状态下不存在除重力以外的其他线加速度,所以可以利用此时的加速度计输出对当前的滚转角和俯仰角做出估计,从而对滚转角误差δφ和俯仰角误差δθ进行观测更新。同时,当准静止磁场检测器检测到磁干扰时,使用单纯依靠捷联航向的HDE算法对航向角误差δψ进行观测更新;否则,使用MC算法对航向角误差δψ进行观测更新,算法工作原理如图2所示。

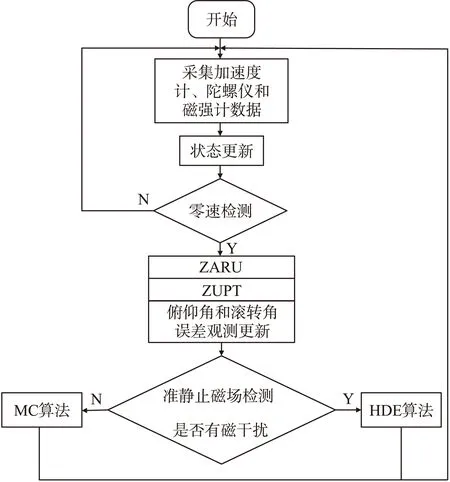
图2 iIEZ+框架工作原理图

1.1 零速检测算法

零速检测算法在整个iIEZ+框架中起到关键作用,零速状态的准确判别有助于及时触发EKF,从而对INS误差进行修正,提高系统精度。目前,此类算法大多基于加速度计[10]或者陀螺仪[11],以及加速度计和陀螺仪[3,12-13]。部分学者利用压电、超声波、RF等传感器进行零速检测。

本文采用文献[12]中所述方法进行零速检测,即利用三轴加速度计和三轴陀螺仪信号共同判断。

1.2 准静止磁场检测算法

假定导航坐标系x轴沿着地球子午面指向北极方向;y轴垂直于子午面指向东向;z轴垂直于xoy平面指向地心,如图3所示。

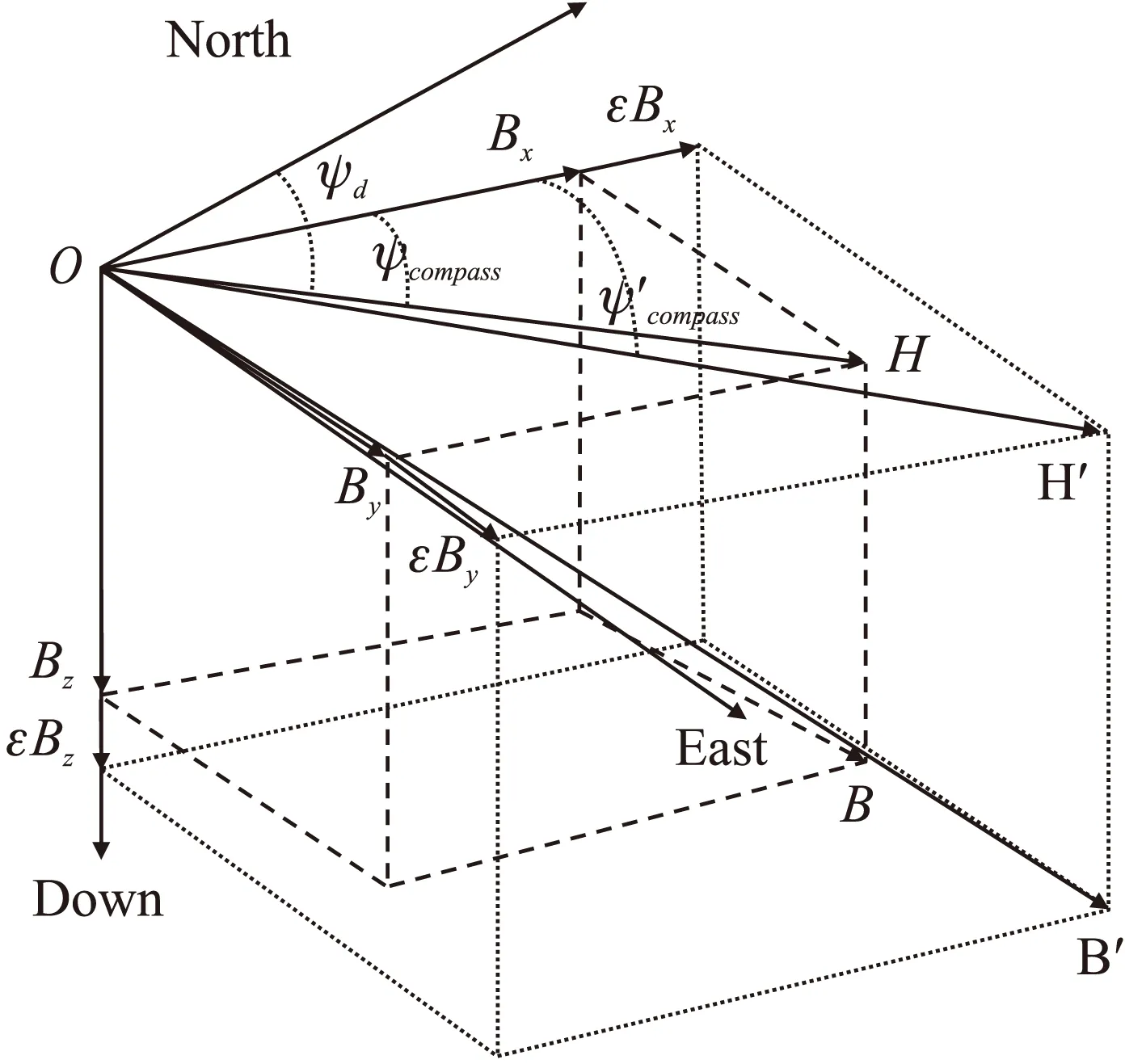
图3 存在干扰的地球磁场模型

(1)

针对此类问题,Afzal等人提出了准静止磁场检测方法,经过大量实验验证,具有很好的识别效果[8]。文中将磁场强度为定值或者随时间缓慢变化的磁场定义为准静止磁场。这种磁场用数学表达式描述如下:

(2)

式中:Bk为k时刻的磁场强度;Bk-1为k-1时刻的磁场强度;Δt为采样时间间隔。假定检验条件H0表示非静止磁场,H1表示准静止磁场,将准静止磁场的检测问题等效为二元假设检验问题。与这两种假设相关的概率密度函数分别为:

(3)

(4)

但是由于建筑物内部存在钢筋结构或者铁磁性物体等,它们产生的磁场干扰往往是稳定的,即所谓的硬磁干扰。如图3所示,当地球磁场的x轴和y轴方向受到稳定的εBxεBy时,H会指向稳定的错误方向。若此时足部在该区域内处于零速状态时,虽然满足上述准静止磁场条件,但是计算出的地磁航向角是错误的。因此,单纯依靠Afzal等人提出的准静止磁场检测方法并不可靠。

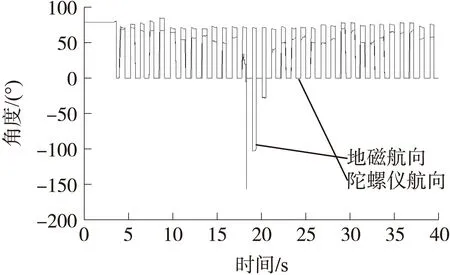
图4 走廊内直线行走时地磁航向和陀螺仪航向对比

图4为由安装在足部的IMU在走廊内直线行走时计算所得零速时刻的陀螺仪航向角和地磁航向角。本图仅对零速时刻的数值进行显示,其他时刻的数值显示为零,所以呈现锯齿状。由图4可以看出,第17 s到20 s时,地磁航向角发生很大变化,同时在一段时间内保持稳定,说明此时遭遇硬磁场干扰。因此,本文在Afzal准静止磁场检测方法的基础上,加入地磁航向和陀螺仪航向差值的阈值条件,如式(5)所示:

Δψgc=|ψgyro-ψcompass|≤ξgc

(5)

当同时满足式(4)、式(5)时,地磁航向角的变化趋势接近于捷联航向角且地磁场强度变化平稳,说明此时处于有效平稳的纯净地磁场中,可以计算得到较为精确有效的地磁航向角,进而触发地磁修正算法;否则,说明此时存在其他磁场干扰,触发启发式航向漂移修正算法。用表达式描述如下:

(6)

图5为Afzal提出算法与本文提出算法检测效果对比;图中仅对零速状态时通过准静止磁场计算得到的航向角进行显示,其他时刻显示为零。可以看出,第20 s时Afzal所提算法将此时的错误磁场误认为是有效的准静止磁场,而本文提出的改进算法能够做出有效判断,将此错误滤除。

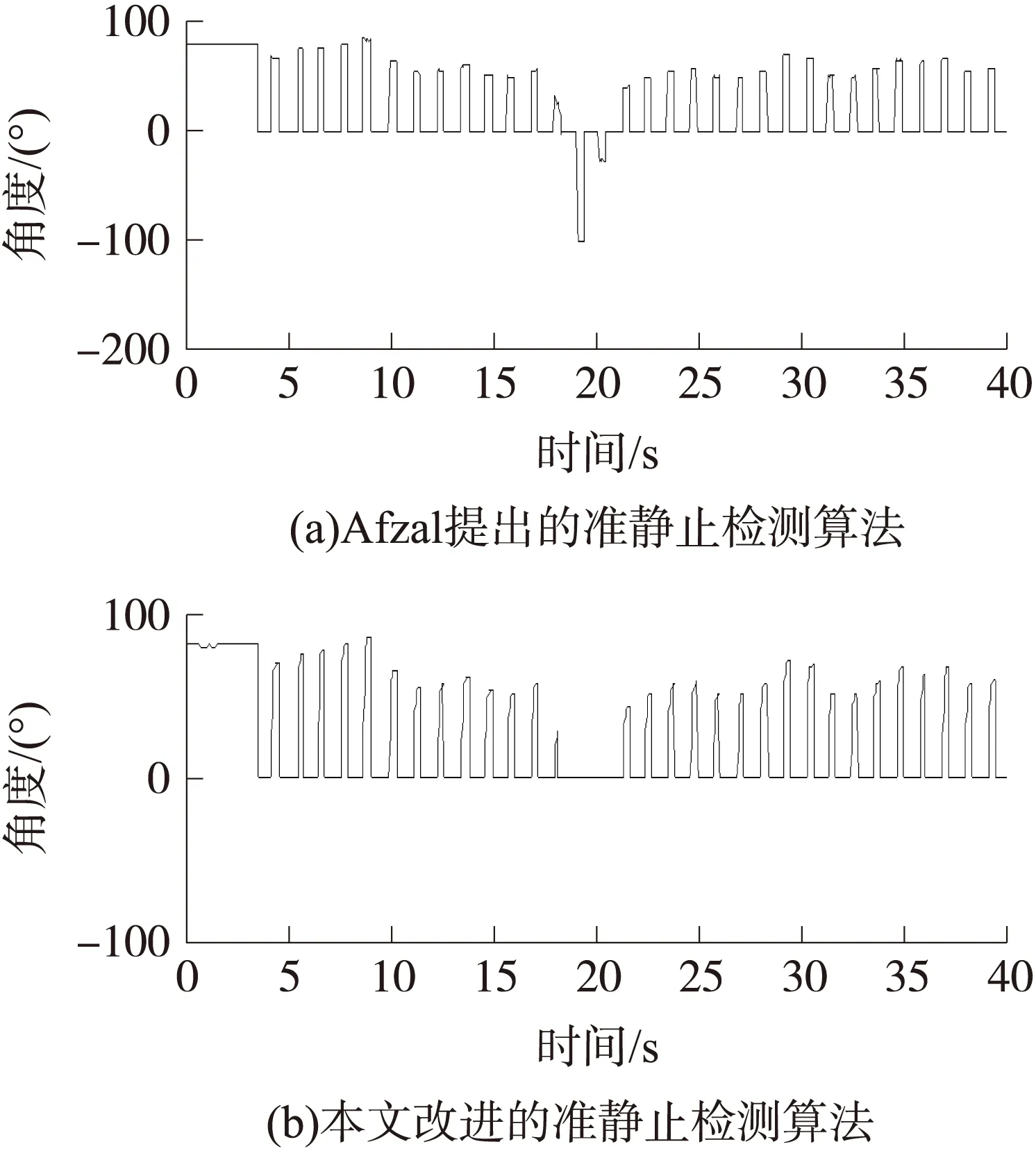
图5 Afzal算法与本文算法检测效果对比

1.3 ZUPT&ZARU

1.4 姿态修正

选取北、东、地分别作为导航坐标系(n系)3个轴的正方向;载体坐标系(b系)固连在传感器上,选取身体的前、右、下3个方向作为坐标轴正方向,如图6所示。

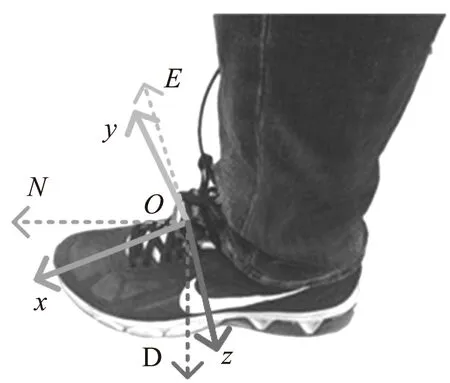
图6 坐标系选取

依次绕z轴、y轴、x轴旋转,得到从n系到b系的方向余弦矩阵:

(7)

式中:φ、θ、ψ分别表示滚转角、俯仰角和偏航角。

1.4.1 滚转角和俯仰角误差修正

由于零偏误差的影响,由陀螺仪输出计算得到滚转角和俯仰角的误差会随时间累积。本文采用加速度计输出计算滚转角和俯仰角。当足部处于零速状态时,比力矢量f在导航坐标系下的投影等于重力加速度,可以表示为:

(8)

由此求得滚转角φ和俯仰角θ为:

(9)

(10)

选取EKF的滚转角和俯仰角误差观测量为:

(11)

1.4.2 MC算法

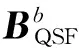
(12)

由此可以得到地磁场强度B在n系北向和东向的分量:

(13)

(14)

选取EKF的航向角误差观测量为:

Δψcompassk=ψgyrok-ψcompassk

(15)

式中:ψgyrok为k时刻由陀螺仪输出计算得到的捷联航向角。

1.4.3 简化后的HDE算法

当遭遇磁场干扰时,单纯依靠磁强计无法计算得到正确的航向信息,如图3所示。在本文提出的iIEZ+框架中,此时切换使用依靠捷联航向的启发式航向漂移消除算法。启发式航向漂移消除算法最早由Borestein等人[18]提出,后来演变出很多改进版,比如利用对室内行走主要方向的置信度匹配最优航向的iHDE算法[19],以及针对人体不同运动行为采取不同的误差补偿算法的AHDE算法[9]。

本文简化了AHDE算法,通过两个复步间的航向角差值将人体的步行运动简单区分为直线运动和转向运动。当行人做直线运动时,理想情况下相邻两个零速状态Rn-1、Rn(如图7所示)的航向角相等,但是由于陀螺仪零偏误差累积,实际计算得到的航向角会出现一定偏差Δψk,如图8所示。若Δψk在一定的阈值范围内,说明人体在做直线运动,认为该偏差是由陀螺仪零偏误差累积造成的;超过阈值,认为人体在做转向运动。

图7 人体步行运动示意图

图8 相邻零速状态及其航向角示意图

相邻两个零速状态的航向角偏差Δψk可以表示为:

(16)

当|Δψk|在阈值ξ范围内时,认为该误差是直线行走过程中由于陀螺仪零偏误差累积造成的航向漂移误差;当|Δψk|大于阈值ξ时,认为行人在做转向运动,该误差角为实际的转向角度,所以此时航向角观测向量为零。

此时EKF的航向误差观测量ΔψHDEk可以表示为:

(17)

1.4.4 扩展卡尔曼滤波器

(18)

线性化处理后的系统状态方程为:

δxk|k-1=Φkδxk-1|k-1+wk-1

(19)

(20)

系统观测方程为:

zk=Hδxk|k+nk

(21)

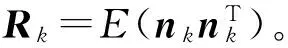
滤波器更新方程为:

δxk|k=δxk|k-1+Kk(zk-Hδxk|k-1)

(22)

式中:δxk|k表示k时刻误差状态向量的后验估计;Kk表示k时刻的卡尔曼增益。

由于地磁修正算法和启发式航向漂移消除算法的观测转移矩阵相同,所以系统观测转移矩阵可以写为:

(23)

误差观测向量为:

(24)

式中:姿态误差观测量Δφk=[Δφk,Δθk,QSF·Δψcompassk+(1-QSF)·ΔψHDEk]T。

观测噪声的协方差矩阵为:

(25)

2 实验

2.1 实验条件

为了验证算法的有效性,本文进行了实际的2D行走实验。使用的IMU为SBG公司生产的IG-500N,包含三轴加速度计、三轴陀螺仪和三轴磁强计。

表2 IMU具体性能指标

IMU被安装在测试者的左脚脚背处,如图6所示。实验场地为北京信息科技大学教二楼一层室内外场地。测试者从楼内起点出发,行走至楼外,最后返回楼内起点,路程总长度约为193 m。

2.2 实验结果

图9中黑色曲线表示磁强计测得实验场地内的地磁场强度模值;红色部分表示本文提出准静止检测算法的检测结果。图10为72 s～75 s内的准静止磁场检测结果,可以看出磁场数据变化基本平稳。

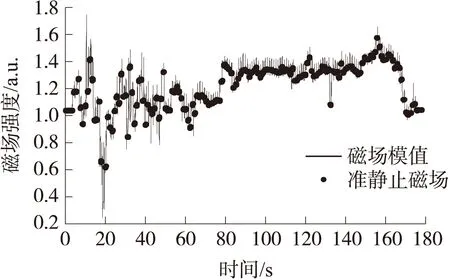
图9 行走准静止磁场检测结果

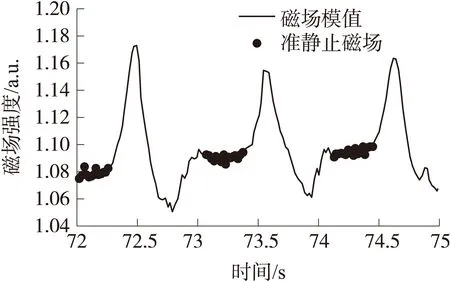
图10 72 s～75 s内准静止磁场检测结果

本文对IEZ、IEZ-ZARU+compass和iIEZ+ 3种算法框架的定位效果进行对比,如图11所示。同时,比较了IEZ-ZARU+compass和iIEZ+算法框架每个零速时刻计算所得平均航向角与真实值的偏差,如图12所示。IEZ算法框架中,由于缺少对陀螺仪零偏误差的观测,航向漂移误差会不断累积,最终会导致很大的定位误差。IEZ-ZARU+compass单独使用地磁修正算法对航向角误差进行观测,很容易受到地磁干扰的影响。

图12 iIEZ+和IEZ-ZARU+compass零速时刻计算所得平均航向角与真实值偏差

图11 使用基于IEZ框架的多种算法和本文算法定位结果及轨迹对比

由图11、图12中可以看出,由起点向东行走至约30 m处(即第18个左右的零速状态)时该算法计算得到的航向角出现了较大偏差,说明在此处受到了其他磁场的干扰,该框架无法做出有效修正。与上述两种算法相比,本文提出iIEZ+算法计算所得轨迹,与实际路线的吻合程度最高(由图11中轨迹和图12中误差角可以看出),在距起点东向30 m的磁场干扰处能够保持较好的航向。

同时,进行了多次行走实验,并将TTD误差(起始点距离占总路程的百分比)统计在表3中。表中数据显示,IEZ算法框架的TTD误差最大,其次为IEZ-ZARU+compass,iIEZ+算法框架的误差最小。其中,IEZ-ZARU+compass算法框架的TTD误差范围相对于iIEZ+较大,说明单纯依靠磁强计修正航向漂移很容易受到其他磁场干扰的影响,在受到磁场干扰时会导致较大的定位误差。

表3 基于IEZ的多种算法框架TTD误差对比

3 结论

通过在室内外环境中,进行多组测试。实验证明,本文提出的算法框架能够准确检测出平稳磁场,并计算出有效可靠的地磁航向角。同时,针对磁场干扰情况选择不同的航向修正算法,避免了单一依靠地磁修正算法容易受到磁干扰影响或者单一使用启发式航向漂移消除算法在人体转向时容易积累陀螺仪零偏误差的问题,实现了两种常用算法间的优势互补,从而提高了整个系统的定位精度。

[1] Foxlin E.Pedestrian Tracking with Shoe-Mounted Inertial Sensors[C]//IEEE Computer Graphics and Applications,2005. USA:IEEE,2005:38-46.

[2] Rajagopal S. Personal Dead Reckoning System with Shoe Mountedinertial Sensors[C]//Master of Science Thesis,Stockholm,Sweden,2008:1-45.

[3] Jiménez A R,Seco F,Prieto J C,et al. Indoor Pedestrian Navigation Using an INS/EKF Framework for Yaw Drift Reduction and a Foot-Mounted IMU[C]//2010 7th Workshop on Positioning Navigation and Communication(WPNC). IEEE,2010:135-143.

[4] 钱伟行,朱欣华,苏岩. 基于足部微惯性/地磁测量组件的个人导航方法[J]. 中国惯性技术学报,2012,20(5):567-572.

[5] 张新喜,张嵘,郭美凤,等. 基于足绑式 INS 的行人导航三轴磁强计在线校准[J]. 清华大学学报:自然科学版,2016,56(2):211-217.

[6] Zhang L,Su Z,Li Q. Pedestrian Navigation Using iZES Framework for Bounding Heading Drift[C]//Asian Simulation Conference. Springer Singapore,2016:235-244.

[7] Renaudin V,Afzal M H,Lachapelle G. New Method for Magnetometers Based Orientation Estimation[C]//Position Location and Navigation Symposium(PLANS),2010 IEEE/ION. IEEE,2010:348-356.

[8] Afzal M H,Renaudin V,Lachapelle G. Use of Earth’s Magnetic Field for Mitigating Gyroscope Errors Regardless of Magnetic Perturbation[J]. Sensors,2011,11(12):11390-11414.

[9] Ju H J,Lee M S,Park C G,et al. Advanced Heuristic Drift Elimination for Indoor Pedestrian Navigation[C]//2014 International Conference on Indoor Positioning and Indoor Navigation(IPIN). IEEE,2014:729-732.

[10] Jimenez A R,Seco F,Prieto C,et al. A Comparison of Pedestrian Dead-Reckoning Algorithms Using a Low-Cost MEMS IMU[C]//IEEE International Symposium on Intelligent Signal Processing,2009. WISP 2009. IEEE,2009:37-42.

[11] Bebek Ö,Suster M A,Rajgopal S,et al. Personal Navigation via High-Resolution Gait-Corrected Inertial Measurement Units[J]. IEEE Transactions on Instrumentation and Measurement,2010,59(11):3018-3027.

[12] Skog I,Handel P,Nilsson J O,et al. Zero-Velocity Detection—An Algorithm Evaluation[J]. IEEE Transactions on Biomedical Engineering,2010,57(11):2657-2666.

[13] 李超,苏中,朱嘉林. 可穿戴式自主定位技术的零速触发算法研究[J]. 传感技术学报,2014,27(5):627-632.

[14] Angermann M,Frassl M,Doniec M,et al. Characterization of the Indoor Magnetic Field for Applications in Localization and Mapping[C]//2012 International Conference on Indoor Positioning and Indoor Navigation(IPIN). IEEE,2012:1-9.

[15] Ladetto Q,Merminod B. Digital Magnetic Compass and Gyroscope Integration for Pedestrian Navigation[C]//9th international Conference on Integrated Navigation Systems,St-Petersburg. 2002.

[16] Afzal M H,Renaudin V,Lachapelle G. Magnetic Field Based Heading Estimation for Pedestrian Navigation Environments[C]//2011 International Conference on Indoor Positioning and Indoor Navigation(IPIN). IEEE,2011:1-10.

[17] Ozyagcilar T. Calibrating an Ecompass in the Presence of Hard and Soft-Iron Interference[J]. Freescale Semiconductor Ltd,2012.

[18] Borenstein J,Ojeda L,Kwanmuang S. Heuristic Reduction of Gyro Drift in IMU-Based Personnel Tracking Systems[C]//SPIE Defense,Security,and Sensing. International Society for Optics and Photonics,2009:73061H-73061H-11.

[19] Jiménez A R,Seco F,Zampella F,et al. Improved Heuristic Drift Elimination(iHDE)for Pedestrian Navigation in Complex Buildings[C]//2011 International Conference on Indoor Positioning and Indoor Navigation(IPIN). IEEE,2011:1-8.

张立强(1990-),男,硕士,主要研究方向为室内惯性导航、信号检测与处理以及传感器融合等,zhangliqiang@mail.bistu.edu.cn或zlq_bistu1407@163.com;

苏 中(1962-),男,博士生导师,博士,本文通讯作者,主要研究方向为惯性器件、高动态IMU和组合导航等,sz@bistu.edu.cn;

李 擎(1964-),女,硕士生导师,博士,主要研究方向为导航与控制的机器学习、自主导航与控制等,liqing@bistu.edu.cn。

Pedestrian Navigation Framework iIEZ+ Based on Quasi-Static Magnetic Field Detection*

ZHANG Liqiang,SUZhong*,LI Qing
(Beijing Key Laboratory of High Dynamic Navigation Technology,University of Beijing Information Science and Technology,Beijing 100101,China)

To eliminate the heading drift error of pedestrian navigation inertial system,magnetic correction algorithm is a valid method. But magnetic disturbance may lead to heading error,and the accuracy of heading is a key factor of the whole inertial system. To solve the problem,the improved quasi-static magnetic field detection method is proposedon the basis of Afzal’s to choose magnetic correction algorithm(MC)or Heuristic Drift Elimination algorithm(HDE),which implements the complementation of two methods. The detection method is integrated into IEZ+ framework proposed by A.R. Jiménez,which forms a new framework named iIEZ+. The iIEZ+ method was tested in several indoor and outdoor environments and has a good performance under magnetic disturbance scenarios. It is able to offer reliable heading and position information. The positioning errors are about 0.6%～1.6% of the total travelled distance,which are better than other methods based on IEZ framework.

pedestrian inertial navigation;quasi-static magnetic field detection;extended Kalman filter;magnetic correction;heuristic drift elimination;magnetic disturbance

项目来源:国家自然科学基金项目61471046;北京市教委市属高校创新能力提升计划项目(TJSHG201510772017)

2016-10-10 修改日期:2016-12-14

TP212.9

A

1004-1699(2017)04-0542-08

C:5100

10.3969/j.issn.1004-1699.2017.04.010