基于压电陶瓷相位调制器的外调制相位生成载波法研究*

巩玲仙,邵贵成,田竹梅,王春灿,付建梅,王爱珍(.忻州师范学院电子系,山西 忻州 034000;.北京交通大学光波技术研究所,北京 00094)



基于压电陶瓷相位调制器的外调制相位生成载波法研究*

巩玲仙1*,邵贵成1,田竹梅1,王春灿2,付建梅1,王爱珍1
(1.忻州师范学院电子系,山西 忻州 034000;2.北京交通大学光波技术研究所,北京 100094)

对基于压电换能器PZT(Piezoelectric Transducer)的外调制相位生成载波PGC(Phase-Generated Carrier)法进行了深入的理论分析和实验研究。PZT光纤相位调制器利用电致伸缩效应来改变缠绕在其上面的光纤的长度,进而实现对光纤中光相位的周期性调制。在马赫曾德尔光纤干涉仪MZI(Mach-Zehnder Interferometer)的参考臂中加入该光纤相位调制器便可以将载波信号调制到光纤干涉仪的输出信号当中。计算机仿真分析了调制参数对PGC解调结果的影响。并通过实验验证了这种调制解调方案的可行性。利用美国国家仪器公司的数据采集系统及Labview编写的解调算法,在臂长为200 m的MZI中成功实现了相位解调,恢复出MZI传感臂中的原始相位信息,解调信号与原始信号的相关系数在0.99以上。

压电换能器;相位生成载波;光纤干涉仪;相位解调

干涉型光纤传感器通过检测光纤中光波相位的变化来测量外界的物理量,相比其他类型的光纤传感器具有频带宽,灵敏度高,动态范围大和易于长距离传输等优点,因此干涉型光纤传感器在周界预警、光纤水听器和分布式光纤传感等方面得到了广泛的研究与应用[1-10]。在干涉型光纤传感器中,传感信息包含在干涉信号的相位当中,为了准确有效地恢复传感信息,相位解调技术对于干涉型光纤传感器来说至关重要。现有的解调技术当中主要有主动零差法、合成外差法、伪外差法、3×3解调法和PGC法[11-12]。其中PGC零差解调法因其具有的诸多优点而受到了广泛的关注。PGC方法最突出的优点是在传感信号带宽外引入了一个大幅度的载波信号,这样一来就可以消除由大幅度环境噪声引起的信号衰落的影响[13]。目前,PGC调制方案主要分为内调制和外调制两种。内调制方法中,通过对激光器加载一个低频调制,然后将光信号输出到不等臂的光纤干涉仪当中的方法来生成相位载波。这种方法的一个优点是光路部分可以实现全光纤化,不需要额外的有源器件。但是这种方法也存在一定的弊端。首先,在调制光频的同时,光源的输出功率受到一定的影响,即伴生调幅现象[9];其次,内调制方式需要可调谐的激光器,这种激光器价格昂贵,传感器系统成本较高;最后,该方法需要光纤干涉仪存在一定的臂长差,增加了干涉仪的相干噪声。外调制方式的PGC方案主要是通过在光纤干涉仪参考臂中加入一个光纤相位调制器来实现载波调制。这种方法虽然在光路中引入了有源器件,但相比内调制方式更加经济。同时,外调制方式可以实现零光程差,这对于降低干涉仪输出的相位噪声十分有利。因此,外调制方式的PGC方法在对于不需要实现全光纤化的场合更加经济适用。

本文对基于PZT光纤相位调制的外调制PGC方法进行了研究。我们首先对PZT光纤相位调制器的原理及PGC解调原理进行了分析,在此基础上,通过数值方法仿真分析了3种调制参数对于解调结果的影响,进而通过实验验证了该外调制方案的可行性和有效性。

图1 外调制PGC原理框图

1 调制解调原理

外调制方式的PGC方案原理框图如图1所示。在PZT上缠绕一定匝数的普通单模光纤构成光纤相位调制器。该光纤相位调制器放置在MZI的参考臂当中。C1,C2为3-dB宽带耦合器。光源输出端加入一个隔离器,以防止反射光对光源的影响。同时,为了降低由光纤干涉仪臂长差产生的相位噪声,在传感臂当中熔接一段与缠绕在PZT上等长的普通单模光纤。

光纤干涉仪两臂的相位差可以表示为:

(1)

式中:n为光纤纤芯的有效折射率;l为光纤干涉仪的臂长差;v为光频;c为真空中的光速。从式(1)中可以看出,干涉仪的相位差主要由3种因素决定,即有效折射率的变化,臂长差的变化和光频的变化。在外调制方式当中相位的变化主要由缠绕在PZT上的光纤长度的变化引起。因此式(1)可以写为[14]:

(2)

这里ξ为光纤的应变系数。PZT在加载驱动信号后,由于电致伸缩效应使得缠绕在其上的光纤受到周期性径向应力的作用,光纤长度将发生周期性改变。假设驱动信号为U0cos(ωct),则光纤长度变化可以表示为:

Δl=kU0cos(ωct)

(3)

k为长度变化系数。则干涉仪两臂的相位差可以表示为:

Δφ=Ccos(ωct)

(4)

I=A+Bcos[Ccos(ωct)+φ(t)]

(5)

式中:A和B是与输入光强和耦合器分光比等有关的常量。φ(t)是外界传感信号引起的相位变化与干涉仪初始相位及相位噪声的和,即:φ(t)=φs(t)+φ0(t)+φn(t)。式(5)中的干涉信号经光电探测器后转换为电压信号后进入数据采集系统转换为数字信号进行解调处理。相位生产载波方法的解调原理图如图2所示。

图2 PGC解调原理框图

B2J1(C)J2(C)φs(t)

(6)

若调制信号频率存在一个初相位t0,则解调结果为[17]:

B2J1(C)J2(C)cos(ωct)0cos(2ωct0)φs(t)

(7)

可见,调制信号的初相位相当于仅在解调结果当中引入了一个缩放系数。当调制信号不稳定时,调制频率与混频信号存在一个频差Δω,则PGC解调算法中经过低通滤波后的结果分别为:

-BJ1(C)cos(Δωt)sinφ(t)

(8)

-BJ2(C)cos(2Δωt)cosφ(t)

(9)

可以看出,低通滤波后的结果中含有Δω和2Δω的成分,微分交叉相乘后并不能消除。因此解调结果将会因此而失真。

图3 不同调制深度下的解制结果和1,2阶Bessel函数的乘积

2 计算机仿真

为了验证PGC算法的有效性,以及调制参数对解调结果的影响,我们利用Matlab编写了PGC仿真程序,通过数值方法来研究外调制方式中调制频率,调制深度和初相位对解调结果的影响。首先我们来分析调制深度C对解调结果的影响。从式(6)中可以看出,解调结果中含有系数项B2J1(C)J2(C),因此,调制深度C将通过该系数项来影响解调结果。设置仿真参数如下:A=B=1;调制频率fc=13.6kHz;φ0=π/3;φs(t)为线性调频信号频率由50Hz～1kHz线性变化。不同调制深度C时的解调结果如图3所示。从图3(a)中可以看出,不同C值时,解调结果仅存在幅度上的差异。但是解调结果的幅度并不是随C线性变化的。这是由于解调结果是与B2J1(C)J2(C)线性相关的。图3(b)给出了不同C值下1阶与2阶Bessel函数乘积。在C值约为2.4的点,乘积达到最大值。这与图3(a)中的结果是相一致的。值得一提的是,PGC解调算法中,最佳的调制深度值就在2.4左右。

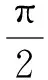
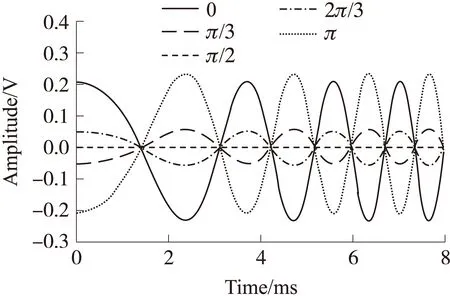
图4 不同的调制信号初始相位对解调结果的影响

图5 不同频率偏差对解调结果的影响

在实际实验当中,由于驱动电源的不理想等原因,实际的调制信号频率并不是理想的单频。因此有必要对调制频率偏差的解调结果的影响进行分析。式(8)和式(9)为低通滤波后的结果,其中含有Δω和2Δω的时间项,微分交叉相乘后并不能消除该项,因此解调结果将有可能产生失真。设置其他仿真参数同上,t0=0。Δω分别为调制频率的0,1‰和5‰倍时的解调结果如5所示。解调信号与原始信号的相关系数分别为:0.942,0.784和0.528。可以明显地看出,频率偏差对解调结果影响非常之大,频率偏差越大解调失真越明显。因此,在实际实验当中,应当选择频率稳定性好的驱动源作为PZT的驱动信号,这样可以使得调制的载波信号频率相对稳定,减少频率偏差对解调结果的不利影响。

3 实验与讨论

3.1 PZT调制深度测量

本文中采用的PZT相位调制器为圆筒状相位调制器。将一定长度的普通单模光纤敷绕在圆筒状PZT上,PZT在通电后由于电致伸缩效应产生沿径向的形变,进而拉伸敷绕在其上面的单模光纤。单模光纤由于纵向应变效应、径向泊松效应和弹光效应等产生其导波模式相位的变化,进而实现相位调制。式(3)中只考虑了3种效应中最主要的应变效应。由式(4)可以看出,基于PZT的光纤相位调制的调制系数C正比于PZT驱动信号。因此为了简化分析,在实验中我们忽略与调制深度C相关的具体参数,而是通过实验的方式,直接测量给定的光纤相位调制器的调制深度。在PZT调制深度的测量实验中,PZT上共计敷绕了100m普通单模光纤。我们将该制作好的光纤相位调制器放置在非对称的MZI当中,MZI由一个1×2 3-dB耦合器和一个3×3耦合器构成。PZT加载频率等于其谐振频率的交流驱动信号,其产生的周期性相位变化通过3×3解调算法得到。

实验中在PZT上敷绕单模光纤主要通过人工敷绕和拉丝塔机械敷绕两种方式实现。两种敷绕方式最大的差别在于拉丝塔的机械敷绕方式在敷绕过程中对光纤施加了纵向应力,因此相比于人工敷绕方式,机械方式能够获得更大的应变系数ξ。此外,机械敷绕方式一致性更好,敷绕的光纤更加整洁。实验测得两种敷绕方式调制深度与加载电压信号U0的关系如图6所示。

图6(a)为人工敷绕的光纤相位调制器,可以看出在50mV～550mV的范围内,调制深度近似正比于调制电压U0。但是实验结果偏离拟合结果相比图6(b)非常明显。图6(b)中在50mV～350mV的范围内,调制深度随U0线性增加。但是在U0大于350mV后,PZT径向形变超过单模光纤应变响应范围,调制深度不再随U0线性增加。对比图6可以看出,机械敷绕方式明显优于人工敷绕方式,虽然人工敷绕方式在350mV～550mV范围仍近似线性,但是机械敷绕方式的线性度更好,并且在线性响应范围内,相同电压下机械敷绕方式的调制深度明显高于人工敷绕方式。因此后续实验中采用机械敷绕方式制作的光纤相位调制器。

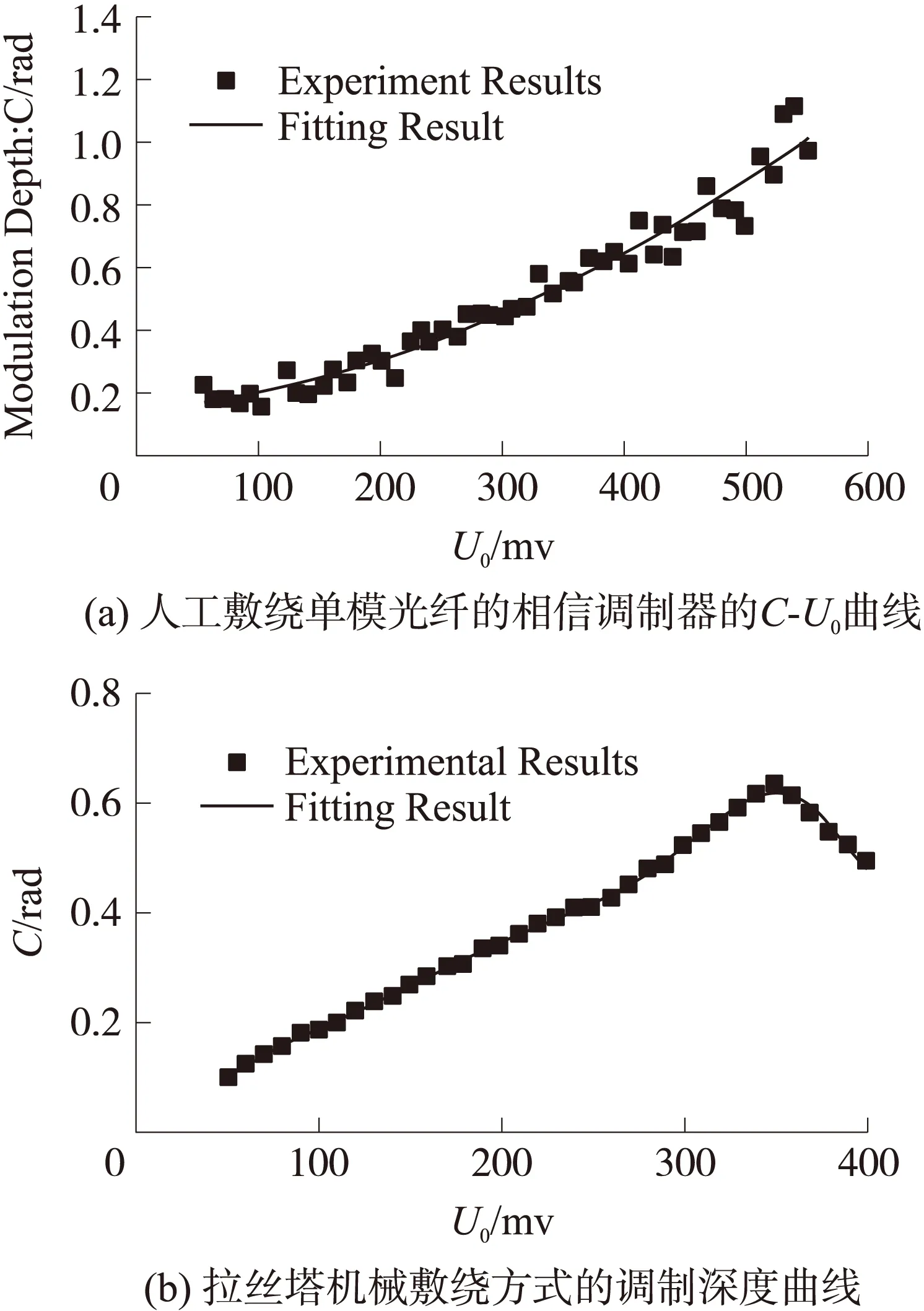
图6 C-U0曲线和调制深度曲线

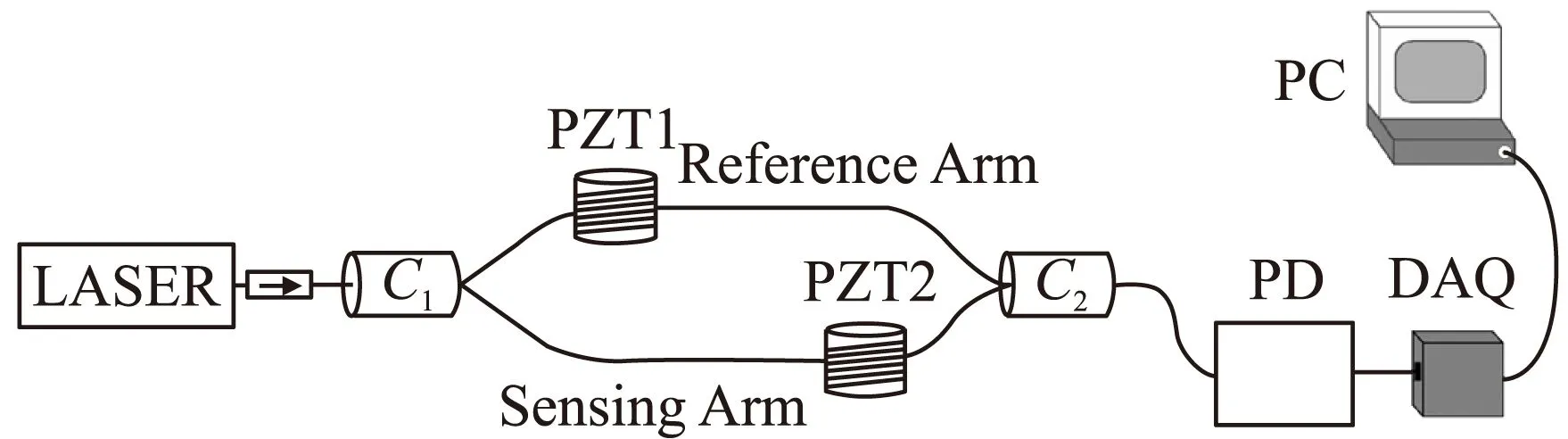
图7 实验框图

3.2 外调制PGC解调

为了验证基于PZT光纤相位调制器的外调制PGC方法的有效性,我们搭建了如图7所示的实验结构进行了实验。其中PD为光电探测器阵列,DAQ为美国国家仪器公司的数据采集系统,采样率为1MHz,PC为工控机。PZT1用做光纤相位调制器,其谐振峰值频率为13.6kHz,共计缠绕了100m普通单模光纤。PZT2用于产生低频相位信号,其工作原理与PZT光纤相位调制器相同,采用1kHz信号源驱动。MZI两臂等长,其长度约为200m。激光器为DFB激光模块,中心波长为1 550nm。在第3部分仿真分析中我们知道,解调过程中如果混频信号与载波调制信号存在频率差,解调结果将会出现失真。为了避免这一问题,在实际实验中我们同时采集了PZT1的驱动信号,将采集到的信号归一化后作为混频信号的输入。这样一来就可以保证载波信号和解调过程中的混频信号同频同相,避免了解调结果失真的问题。光电探测器探测到的原始干涉信号及相应的解调结果如图8所示。

从图8(a)中可以看出,该光纤相位调制器的调制效果非常理想。图8(b)为经过PGC解调得到的信号,其频率为 1kHz,这与PZT2的驱动信号相同。这就同时说明了光纤相位调制器的可靠性和解调算法的有效性。为了更加准确的说明解调结果,我们利用DAQ同时采集了PZT2的驱动信号,将解调结果与PZT2的驱动信号进行互相关分析运算,计算得到相关系数见图9。图9中相关系数的最大值达到0.995,这就更加证实了我们的论断。图10给出了解调结果的功率谱。

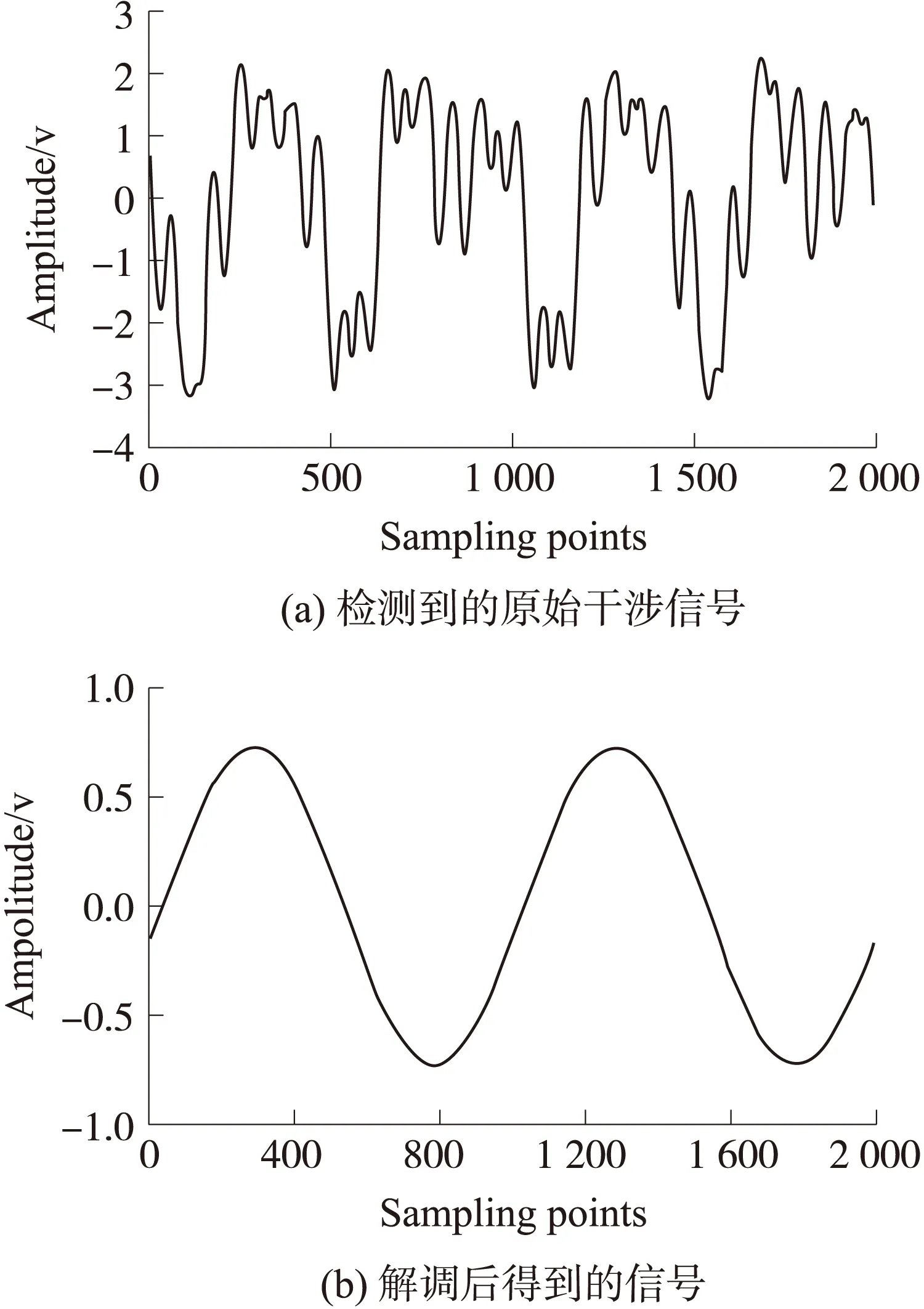
图8 信号处理

图9 解调结果与原始信号相关系数,最大值0.995

图8中的结果采用了已知的单频信号作为传感信号进行了PGC解调。图9和图10的结果表明外调制PGC方法对于单频传感信号的解调十分有效。但是在实际应用当中,被传感信息往往不是理想的单频信号,而是含有复杂的连续频率成分。因此,为了进一步验证PGC外调制方法的有效性,我们测试了该方法对于随机信号的解调能力。由于扰动的随机性,我们无法得知光纤干涉仪中具体的相位变化。因此在实验当中我们采用一个非对称MZI作为参照,将相同的随机扰动分别作用在非对称MZI和外调制PGC方案中,利用成熟的3×3解调算法解调出随机扰动产生的随机相位变化。进而利用PGC方法解调出相同的随机信息。图11(a)为3×3方法解调出的单次随机扰动产生的信号,图11(b)为利用外调整PGC方案解调出来的随机信号,两者的相关系数为0.997。图11(c)为解调出的随机信号的功率谱,可以看出该随机信号为中心频率在60Hz的宽频随机信号。图11的解调结果表明外调制PGC方案具有良好的解调性能。

图10 解调信号的功率谱

图11 随机信号的处理

4 结论

本文对基于PZT光纤相位调制器的外调制方式的PGC方法进行了仿真分析和实验研究。PZT光纤相位调制利用电致伸缩效应周期性的改变缠绕在其上面的光纤的长度来实现相位调制。仿真分析表明,调制深度,初始相位及频率偏差均会对解调结果产生影响,最佳调制深度由1、2阶Bessel函数乘积决定,约为2.4左右。初始相位有可能使解调结果为0,很小的频率偏差都将使解调结果产生失真。在实际实验当中,外调制方式的PGC方法解调结果十分理想,解调信号与原始信号的相关系数达到0.99以上。该外调制方式的PGC方法在干涉型光纤传感器的相位解调方面有一定的实用价值。

[1] 毛红鸿,崔磊,金伟良,等. 基于分布式光纤传感的混凝土裂缝识别与监测试验研究[J]. 传感技术学报,2014,27(9):1298-1304.

[2] 吕舜,娄莉凤,王超. 全光纤干涉振动信号测试系统的硬件解调系统的研究[J]. 传感技术学报,2013,26(7):932-935.

[3] 韩玲娟,王强,杨其华,等. 基于分布式光纤传感的水下输气管道泄漏检测与定位分析[J]. 传感技术学报,2015,28(7):1097-1102.

[4] 曾红燕,沈常宇,路艳芳,等. 基于保偏光纤马赫曾德干涉结合布拉格光纤光栅的折射率传感器[J]. 传感技术学报,2015,28(11):1727-1731.

[5] 叶子,王超. 用于监测阀门泄漏的超高动态范围全光纤超声传感系统[J]. 传感技术学报,2016,29(7):957-961.

[6] 罗光明,张春熹,马宗峰,等. 分布式光纤安防系统传感和定位技术研究[J]. 压电与声光,2008,31(3):327-329.

[7] 周琰,靳世久,曾周末,等. 分布式光纤管道安全检测定位技术研究[J]. 光电子·激光,2008,19(7):922-924.

[8] 李玉深,周波,李绪友. 干涉型光纤水听器相位载波解调技术[J]. 传感器技术,2004,23(2):14-17.

[9] 曹家年,张立昆,李绪友,等. 干涉型光纤水听器相位载波调制及解调方案研究[J]. 光学学报,2008,19(11):1536-1540.

[10] 杭利军,何存富,吴斌,等. 新型分布式光纤管道泄漏检测技术及定位方法研究[J]. 光学学报,2008,28(1):123-127.

[11] Kersey A D,Lewin A C,Jackson D A. Pseudo-Heterodyne Detection Scheme for the Fibre Gyroscope[J]. Electronics Letters,1984,20(9):368-370.

[12] 陈宇,林京,孟强,等. 基于3×3耦合器光纤水听器的数字化解调方案[J]. 仪器仪表学报,2008,29(4):755-759.

[13] Dandridge A,Tveten A B,Giallorenzi T G. Homodyne Demodulation Scheme for Fiber Optic Sensors Using Phase Generated Carrier[J]. Microwave Theory and Techniques,IEEE Transactions,1982,30(10):1635-1641.

[14] 王廷云. 用压电陶瓷实现的光纤相位调制理论与实验分析[J]. 光子学报,1999,28(2):134-137.

[15] 倪明,熊水东,孟洲,等. 数字化相位载波解调方案在光纤水听器系统中的实现[J]. 应用声学,2004,23(7):5-11.

[16] 于晓之,赵旭宏,朱雪峰,等. 干涉型光纤水听器的数字化解调[J]. 应用科技,2007,34(6):18-22.

[17] Huang S C,Lin H. Modified Phase-Generated Carrier Demodulation Compensated for the Propagation Delay of the Fiber[J]. Applied Optics,2007,46(31):7594-7603.

巩玲仙(1987-),女,硕士,2010年获烟台大学学士学位,2013获北京交通大学硕士学位,主要从事光通信、光纤激光器及移动通信的研究,gongfan329@163.com;

王春灿(1975-),男,副教授,博士,硕士生导师,于2008年博士毕业于北京交通大学光波所通信与信息系统专业,1997年毕业于西安电子科技大学电磁场与微波技术专业,主要从事特种光纤器件,光纤激光器,非线性光纤光学器件的研究。

Study of Phase Generated Carrier Method Based on External PZT Phase Modulator*

GONG Lingxian1*,SHAO Guicheng1,TIAN Zhumei1,WANG Chuncan2,FU Jianmei1,WANG Aizhen1
(1.Department of Electronics,Xinzhou Teachers University,Xinzhou Shanxi 034000,China;2.Institute of Lightwave Technology,Beijing Jiaotong University,Beijing 100094,China)

The external modulation phase-generated carrier(PGC)method based on piezoelectric transducer(PZT)is theoretically and experimentally investigated. The PZT phase modulator changes the length of winding fibers by electrostrictive effect to realize periodic phase modulation. The carrier is contained in the output interference signals when the phase modulator is inserted into the reference arm of a Mach-Zehnder Interferometer(MZI). Numerical simulations are carried out to study the influence of modulation parameters on PGC demodulation results. And feasibility of the scheme is verified by experiments. Phase demodulation is successfully achieved in a 200 m long MZI,and the original phase information on sensing arm is recovered by using NI Data Acquisition System and demodulation algorithm written by Labview,the correlation coefficient between demodulation results and original signals is above 0.99.

piezoelectric transducer;phase-generated carrier;optical fiber interferometer;phase demodulation

项目来源:山西省高校“131”领军人才工程项目(智能化交通信号控制系统);忻州师范学院教学改革研究项目(JGZD201509);IAI-CDIO理念下通信类实践课程的教学模式研究项目(J2016097)

2016-09-23 修改日期:2016-11-21

TN29

A

1004-1699(2017)04-0529-06

C:7230E

10.3969/j.issn.1004-1699.2017.04.008