基于过程不确定性的创新型产品定价①

苏 屹,于跃奇,罗小芳

(1.哈尔滨工程大学 经济管理学院,哈尔滨 150001；2.清华大学 经济管理学院,北京 100084；3.江苏科技大学 经济管理学院,江苏 镇江 212003)

1 研究背景

当今时代,科技飞速发展,各类创新型产品层出不穷。但大多数的创新型产品都存在着寿命短难以实现产品商业化的困境,商业化的失败给企业带来重大的经济损失。造成创新型产品商业化失败的原因众多,其中过高的价格造成消费者对创新型产品失去兴趣的主要原因之一,可见如何制定合理的价格是创新型产品取得商业化成功的关键[1]。产品定价问题已经受到学者的普遍关注,大部分研究聚焦于金融类产品的定价问题[2-9]。其中比较有代表性的文献如下:周桦[2]和秦学志[5]等运用风险中性定价法分别研究了万能险万能账户中最低保证收益率期权的公允价值和离散时间下或有可转债的估值方法。汤正洪[3]以小贷公司应付款保函证券化为研究对象,通过引入障碍期权刻画保函的违约特征,建立基于现有证券化产品定价模型中嵌入具有保函投资者特性的支付函数的定价模型。李丹[6]在单因子模型的基础上,结合违约概率和违约损失之间的正相关性的关系,得出容许违约损失服从任意分布的信用风险经济资本的定价方法。郑海涛[7]把传统精算定价理论和金融未定权益估值理论结合,建立了多因素下累积分红寿险合同的公允定价模型和终了分红权的定价模型,证明了终了分红可抑制退保的问题。潘坚[8]利用风险对冲的方法和无套利原理建立了随机回收率与违约强度负相关的公司债券定价模型。胡斌[9]引入熊市价差期权构造原理建立了贷款保险定价模型,提高了贷款保险价格的合理性,弥补了同类定价模型的不足。随着研究的不断深入,学者们从不确定性需求的角度对产品定价问题进行研究[10-13]。同时,范丽繁、张晓娟、唐方成、唐尧和刘晓峰[14-18]等人对网络定价的问题进行了相关的研究。陈立彬、廖成林、Greenleaf、Kopalle、Fibich和Dye[1,19-23]分别在参考价格的角度对产品定价问题进行研究。刘晓峰、王宣涛、巩天啸和Gan[24-27]则考虑了策略型消费者对定价的影响。牟博佼、魏轶华、魏玉和Gallego[28-31]从库存与供应链的角度对产品的定价问题进行了相关的研究。

在现有的研究中大多数学者所用到的定价方法一般是在博弈论[32]的基础上进行的升华。比较主流的模型有 Hotelling模型[16]、Stackelberg模型[24,33]、Cournot模型[13]和Bertrand模型[14]。这些模型都是对两方竞争下的寡头市场进行定价的相关方法。除此之外,王春苹和杜荣[34-35]也基于寡头市场的定价问题进行了研究。诸如Myklebust和Shioda[36-38]等一些研究人员运用效用最大化原理和启发式算法研究定价问题。然而,创新型产品不同于一般商品,Fisher按照需求类型把产品分为功能型和创新型,创新型产品相对于功能型产品有着较短的生命周期,通常有较高的边际利润,需求波动较大[39-40]。因此创新型产品在生命周期各阶段都存在着严重的不确定性,伴随着替代品的出现导致这种不确定性更加复杂。基于对此问题的分析,结合创新型产品的特点建立动态价格模型。在传统的定价方法——成本加成定价法[41-42]的基础上,考虑到创新型产品技术难度大和废品率高的特点对价格的影响,进而确定创新型产品的初始销售价格。在进一步考虑创新型产品需求弹性系数的基础上,对初始销售价格进行适当的修正,结合需求弹性理论[43]确定价格改变的方向和大小。根据企业前期的商品销售情况,使用Bass模型[44-45]对销售情况进行预测,进而确定修正后的初始销售价格持续的时间。本文的研究内容将为企业在对创新型产品的定价决策上提供一定的理论依据和思路方法,以帮助企业实现创新型产品商业化的成功。

2 创新型产品初始销售价格的确定

首先,采用成本加成定价法确定创新型产品的初始销售价格。成本加成定价是指创新型产品单位成本加上规定的利润比例所制定的价格。其中价格与成本之间的差额,就是加成比例,可得P0=C(1+λ),C=C0+V。其中,P0为标准价格,C为总成本,λ为加成率,C0为固定成本,V为可变成本。

创新型产品的固定成本主要包括企业的固定资产折旧、维修费用、工资福利、经销费和经营管理费等,分别设为X1,X2,…,Xn,单位产量为Q,固定成本为C0,单位固定成本为Cq,则有。可变成本V主要包括原材料、天然气、水、电和税费等。可变成本与产量之间存在线性关系,较易计算,不同企业有自己的定额标准。创新型产品的可变成本的计算方法如表1所示。

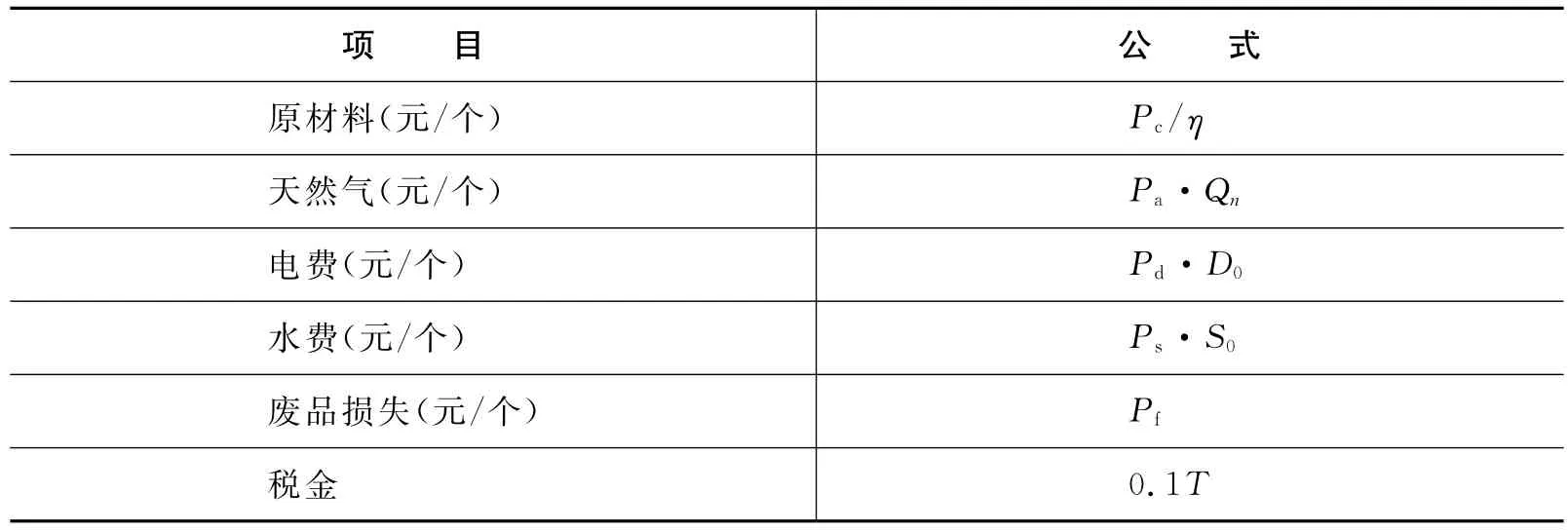
表1 可变成本计算方法

其中:Pc为原材料单价,一般采用加权平均法进行计算；η为材料利用率,根据实际的材料利用率进行计算；Pq为单位天然气的价格；Q0为生产单位创新型产品天然气消耗定额,不同企业有不同的定额,如果没有企业定额可根据专业通用定额或者全国统一定额进行计算；Pd为单位电价格；D0为生产单位创新型产品所用电消耗定额；Ps为单位水价格；S0为生产单位创新型产品所用水消耗定额；pf为废品损失,一般根据废品率计算获得。税金一般是城建税和教育费附加,按单位创新型产品所对应增值税T的10%计算,即0.1T。

故可变成本V的公式如下:

据此,可获得单位创新型产品成本C,即

由于创新型产品属于新开发的所以废品率较高,并且很不稳定,所以应将废品率计入定价的考虑因素中,废品率为F,一般通过加权平均获得,则有P=P0(1+F)。

除此之外创新型产品的生产过程中技术难度和水平都大大领先于一般产品,而且前期的创新投入也比较多,因此要考虑到创新型产品的难度系数对定价的影响。不同的创新型产品的,都有不同的难度系数,产品定价时根据标准价格乘以难度系数Kd即可,P=P0·Kd。

综合考虑以上因素,可得

综上所述,企业可通过确定创新型产品的可变成本、固定成本、废品率和难度系数,进而确定创新型产品的初始销售价格P。

3 考虑需求弹性的进一步讨论

成本加成定价法作为垄断竞争市场的通用方法,如若假定成本等因素保持不变,则其中“平均利润”水平会正确显示消费者偏好[46]。但是,对于创新型产品来说,由于竞争型产品不多、参照系较少,平均利润率无法形成,因此仅凭传统的加成法定价显然不是十分合理[47]。因此本文考虑在需求弹性理论的基础上对创新型产品的初始销售价格P进行修正,进而获得的创新型产品的最优初始销售价格P*。

根据需求弹性理论可知对于企业来讲需求价格弹性指某商品的销售量变动率与其价格变动率之比,主要反映了商品的销售量对价格变动反应的灵敏程度。

式(4)中,Ed为需求弹性系数。

第一,对于缺乏弹性的创新型产品来说具体表现为0＜Ed＜1,一般情况下这类创新型产品是人们的生活必需品,因此无论这种创新型产品价格上不上涨,消费者都会购买则这种创新型产品,所以一般情况下价格上升会使销售收入增加。第二,当创新型产品富有弹性时会表现为Ed＞1,此时创新型产品有很多替代品,一旦价格上涨消费者就会选择价格相对便宜的其他产品代替创新型产品,进而就会导致需求量下降。所以一般情况下价格上升会使销售收入减少,在这种情况下企业应采取渗透定价策略,快速提高销售量和市场占有率。第三,当Ed=1时说明创新型产品为单一弹性产品,此时价格的变动不会影响销售收入。

创新型产品在进行价格调整时,应结合本身的需求弹性系数进行分析其价格调整方向和大小。根据需求弹性理论则有如下推导过程(Δπ＞0时销售总利润增加)。根据需求弹性公式,可得

将式(5)代入式(6),可得

(1)当0＜Ed＜1时,应采用涨价的调整策略来促进销售中利润的增加,且涨价量Δp的调整幅度区间为

(2)当Ed=1时,应采用涨价的调整策略来促进销售中利润的增加,涨价幅度小于单位可变成本即可。

(3)当Ed＞1时,应采用降价的调整策略来促进销售中利润的增加,且降价量Δp的调整幅度区间为

(4)在降价和涨价的措施中,求Δπ对Δp的二次导数,得

即为使得总利润增量达到最大值的价格调整量。

由此可得最优初始销售价格P*=P+ΔP,即当企业明确创新型产品的需求弹性系数,就可以结合需求弹性理论对创新型产品的初始销售价格P进行修正,进而获得更加合理的最优初始销售价格P*。

4 创新型产品最优初始销售价格的持续时间

按照市场竞争理论,创新型产品获得超额价值后,会有大批的企业进行模仿跟进。市场上会出现一批模仿创新型产品,模仿创新型产品避免了初始创新的风险,因此具有更低的投入成本。同比情况下,模仿创新型产品比创新型产品具有更低的价格,以获得竞争优势。在市场上表现为创新型产品的消费者购买比率下降,当比率不断下降的过程中,为了实现利润最大化的目标,企业必须对创新型产品的售价进行改变。本节主要对创新型产品的最优初始销售价格P*的持续时间进行确定。一般情况下可通过对销售量的预测获得价格变动临界点,进而确定最优初始销售价格P*的持续时间。首先,需要确定创新型产品的销售量。需要注意的是,创新型产品不同于普通产品,它的销售过程具有极大的不确定性,因此并不能通过已有的经验对创新型产品的销售情况进行预测。基于此,本文将以美国的Frank Bass教授提出的Bass模型对该创新型产品的销售情况进行预测,进而确定创新型产品的最优初始销售价格P*的持续时间。

4.1 模型假设

本研究主要基于以下假设:

不考虑创新型产品的二次创新,即创新型产品使用性能随时间的推移保持稳定(H1)；

扩散只有两种结果,创新型产品商业化扩散成功和创新型产品商业化扩散失败(H2)；

该扩散不受创新型产品的市场营销策略的影响(H3)；

在整个创新型产品商业化的过程中不存在供给方面的问题(H4)；

创新型产品的购买者是同质的,无差异的(H5)；

该创新型产品的市场潜力随着时间的推移保持不变(H6)；

最优初始销售价格P*在达到价格临界点前保持不变(H7)。

4.2 模型建立

首先给出如下定义:f(T)表示创新型产品在T时刻的购买率；F(T)表示从0到T时刻创新型产品购买者的累计比例,即销售量,；m表示首次购买的最大市场潜力；S(T)表示T时刻的购买者数量S(T)=mf(T)；Y(T)表示T时刻之前购买者的数量Y(T)=mF(T)；Z(T)表示T时刻未购买者将要购买的比例Z(T)=f(T)/(1-F(T))。

Bass模型的基本假定是Z(T)为已购买者的线性函数Z(T)=a+bF(T)。由于T=0时,因此f(T)=a。根据前面的假设,a值反映了创新型产品的购买者对创新型产品商业化扩散的影响,称为创新系数。而bF(T)的值反映了已经购买者对模仿者的影响,因此b被称为模仿系数。

由以上Bass模型的基本假设,可以推导出

f(T)=[a+b·F(T)][1-F(T)]=a+(a-b)F(T)-b[F(T)]2(8)对这个微分方程进行求解可以得出T时刻购买率f(T),销售量F(T)和T时刻购买者的数量S(T)如下:

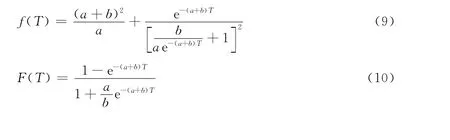
4.3 模型求解

对于上述模型的求解关键是对参数a、b的确定,本文将运用最大似然法对a、b进行参数估计。累积分布函数F(t)仅适用于最终所有人都会购买创新型产品的情况,但是实际生活中有一些人最终不会购买该创新型产品。因此假定最终购买的比例是γ,则新的累积分布函数为G(t)=γF(t),取一个样本量是M的样本。令t0=0,tT=∞,xi表示样本中在(ti-1,ti)(i=1,2,…,T-1)时间段购买者数目。观测的截止时间为tT-1,即XT个个体在tT-1时刻未购买,所以有

令α=a/b,β=a+b,得出似然函数

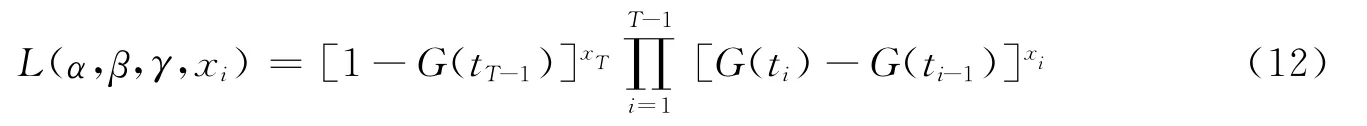
对数似然函数为

α、β、γ的最大似然估计就是使上述对数似然函数取得最大值的。则

当a≤b时,增长曲线无极值点,随时间呈指数衰减状态,说明该创新型产品扩散失败应尽快开发替代品或进行降价处理(如图1所示)。当a＞b时,增长曲线有最高点,即创新型产品商业化获得成功(如图2所示)。

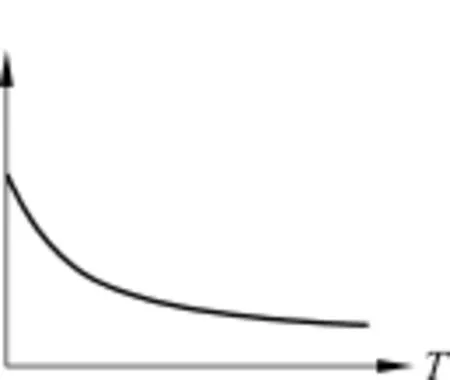
图1 扩散失败

图2 商业化成功

对曲线S(T)进行求导,可得

通过以上分析可知,进行创新型产品生产的企业可以准确地估算出最有价格的持续时间,进而实现企业利润的最大化。在到达T*时刻后,企业通常需要对创新型产品降价的方式以保证稳固的销量,T*是该创新型产品的价格改变临界点,创新型产品最优初始销售价格P*的持续时间为[0,T*]。如果想要继续使得产品具有较强的竞争力,为企业获得更多的利润,可以通过二次创新的途径来实现。

5 结论

创新型产品商业化成功是企业实现可持续发展的关键,科学的制定创新型产品的价格是创新型产品商业化成功的关键影响因素。然而,部分企业在创新型产品完成初步开发后,没有充分考虑创新型产品的需求弹性问题,制定出的价格不够科学,不能使得创新投资最大程度的回收,致使创新型产品商业化的失败。因此,本文在充分考虑创新型产品需求弹性的基础上,提供一种创新型产品定价思路,为企业提供一种可供借鉴的创新型产品定价方法,来实现创新型产品商业化的成功,进而实现企业的可持续发展。本文在不确定性的框架下,基于对创新型产品特点的分析和理解,运用成本加成定价法、需求弹性理论和Bass模型,得出创新型产品的最优初始销售价格P*以及最优初始销售价格P*的持续时间[0,T*],为企业对创新型产品进行科学价格提供了一定的思路。

本文的研究也存在一些不足之处。第一,Bass模型没有价格变量,研究者首先必须在此模型中引入价格,然后才能求解最优定价策略[48]。因此,如果在Bass模型中引入价格变量的方法不适合,那么所获得的“最优”定价策略就不一定是最优的。第二,由于在时间T*之后的价格变动受到是否有二次创新、是否有替代品出现等诸多因素影响,导致创新型产品定价问题更加复杂。作者在今后的研究重点在Bass模型的理论基础上,对需求预测模型进行优化,对时间T*之后的价格变动情况进行具体的分析,进而得到更加准确的创新型产品定价策略。

[1] 陈立彬.创新产品消费者支付意愿分布变动成因研究:参考价格影响的视角[M].北京:经济科学出版社,2013:1-7.

[2] 周桦.中国万能寿险投资账户最低收益率保证与退保期权的定价研究[J].系统工程理论与实践,2013,33(3):557-568.

[3] 汤正洪,何建敏,尹群耀.保函证券化设计与定价——基于投资者视角[J].系统工程,2016(2):51-56.

[4] 史永东,赵永刚.信用衍生产品定价理论文献综述[J].世界经济,2007,30(11):80-96.

[5] 秦学志,胡友群,尚勤.基于转换点生存概率的或有可转债定价研究[J].管理工程学报,2015,29(2):182-189.

[6] 李丹.基于违约概率与违约损失相关的贷款定价[J].系统管理学报,2015,24(1):56-62.

[7] 郑海涛,秦中峰,罗淇耀.多因素下累积分红寿险合同的公允定价模型[J].管理科学学报,2014(12):60-74.

[8] 潘坚,肖庆宪.混合模型下具有随机回收风险的公司债券定价[J].系统工程,2016,34(7):1-7.

[9] 胡斌,史本山,胡艳萍.考虑借款人债务清偿结构的贷款保险定价模型——基于价差期权理论的应用[J].系统工程,2016,34(2):45-50.

[10] 郭军华,杨丽,李帮义.不确定需求下的再制造产品联合定价决策[J].系统工程理论与实践,2013,33(8):1949-1955.

[11] 官振中,任建标.不确定性需求下的易逝性高科技产品定价策略研究[J].系统工程学报,2011,26(1):113-120.

[12] 唐小我,马永开.需求不确定情形下的产品产量和价格的确定[J].中国软科学,2003(2):62-67.

[13] 王增武,汪圣明.结构性金融产品的定价与投资决策研究:不确定性方法[J].金融评论,2010,2(1):66-74.

[14] 范丽繁,王满四.基于Bertrand模型的双寡头商家的团购定价策略[J].系统工程,2016,34(4):62-69.

[15] 张小娟,王勇.预订团购期间零售商的最优定价决策[J].系统工程,2013,31(11):73-77.

[16] 唐方成,池坤鹏.双边网络环境下的网络团购定价策略研究[J].中国管理科学,2013,21(3):185-192.

[17] 唐尧,马士华.网络团购下的定价与持续时间决策[J].管理科学学报,2015,18(9):12-23.

[18] 刘晓峰,顾领.基于消费者转换行为的线上线下产品定价策略研究[J].管理科学,2016,29(2):93-103.

[19] 廖成林,杨毅,李忆.基于内部参考价格调整的新产品定价模型研究[J].商业时代,2014(18):58-59.

[20] GREENLEAF E A.The impact of reference price effects on the profitability of price promotions[J].Marketing Science,1995,14(1):82-104.

[21] Kopalle P K,Winer R S.A dynamic model of reference price and expected quality[J].Marketing Letters,1995,7(1):41-52.

[22] Fibich G,Lowengart O.Explicit solutions of optimization models and differential games with nonsmooth(asymmetric)reference-price effects[J].Operations Research,2003,51(5):721-734.

[23] Dye C Y,Yang C T.Optimal dynamic pricing and preservation technology investment for deteriorating products with reference price effects[J].Omega,2016,62:52-67.

[24] 刘晓峰,徐贤浩.消费者策略行为视角下短生命周期产品的定价机制研究[J].中国管理科学,2011,19(4):152-158.

[25] Gan S S,Pujawan I N,Suparno,et al.Pricing decision model for new and remanufactured short-life cycle products with time-dependent demand[J].Operations Research Perspectives,2015,2(1):1-12.

[26] 王宣涛,张玉林.考虑顾客行为与零售商公平关切的易逝品定价与供应链协调研究[J].管理工程学报,2015,29(1):89-97.

[27] 巩天啸,王玮,陈丽华.面对策略型消费者的产品创新换代策略[J].管理科学学报,2015,18(9):1-11.

[28] 牟博佼,肖勇波,陈剑.基于MNL选择模型的替代产品定价和库存决策研究[J].中国管理科学,2010,18(3):25-32.

[29] 魏轶华,胡奇英.考虑容量决策的多阶段存储定价模型[J].西安电子科技大学学报(自然科学版),2005,32(1):133-138.

[30] GALLEGO G,VAN RYZIN G.Optimal dynamic pricing of inventories with stochastic demand over finite horizons[J].Management Science,1994,40(8):999-1020.

[31] 魏玉.基于碳减排的创新型产品供应链优化研究[D].北京:北京交通大学,2014:10-40.

[32] 杨菊红,郝睿,王旭明.基于产品定价机制的博弈模型[J].复杂系统与复杂性科学,2013,10(2):44-51.

[33] 王华清,李静静.基于感知质量的自有品牌产品定价决策[J].系统工程理论与实践,2011,31(8):1454-1459.

[34] 王春苹,南国芳,李敏强.寡头市场信息产品与服务的最优定价策略[J].管理科学学报,2016,19(3):92-106.

[35] 杜荣,胡奇英,魏轶华.两方竞争情况下产品动态定价研究[J].管理工程学报,2003,17(1):20-24.

[36] Myklebust T G J,Sharpe M A,Tuncel L.Efficient heuristic algorithms for maximum utility product pricing problems[J].Computers&Operations Research,2016,69:25-39.

[37] Shioda R,Tuncel L,Hui B.Applications of deterministic optimization techniques to some probabilistic choice models for product pricing using reservation prices[J].Pacific Journal of Optimization,2007,10(4):767-808.

[38] Shioda R,Tuncel L,Myklebust T G J.Maximum utility product pricing models and algorithms based on reservation price[J].Computational Optimization&Applications,2011,48(2):157-198.

[39] 何龙飞,吕海利,赵道致.创新型产品供应网络运营最优控制与清晰联盟博弈协调[J].计算机集成制造系统,2013,19(5):1091-1104.

[40] Fisher M L.Whatis the right supply chain for your product[J].Harvard Business Review,1997,75(2):105-105.

[41] 马小雄.兰石锻造厂锻件定价方法研究[D].西安:西安理工大学,2009:27-55.

[42] 苏素.产品定价的理论与方法研究[D].重庆:重庆大学,2001:27-28.

[43] 伍希.需求价格弹性在商品定价中的应用研究[J].商场现代化,2011(23):13-14.

[44] Norton J A,Bass F M.A diffusion theory model of adoption and substitution for successive generations of high-technology products[J].Management Science,1987,33(9):1069-1086.

[45] 吕晓玲.消费者行为统计模型分析与案例研究[M].北京:清华大学出版社,2015:10-13.

[46] Varian H R.Intermediate Microeconomics:A Modern Approach[M].New York:WW Norton&Company,2010.

[47] 王真.高技术产品定价模型研究——基于TCO和TVO均衡的视角[J].北京工商大学学报(社会科学版),2016,31(2):117-126.

[48] Krishnan T V,Jain D C.Optimal pricing strategy for new products[J].Management Science,1999,45(12):1650-1663.