2016年高考天津理科压轴题简解的深度揭秘*
安徽省安庆市岳西县汤池中学 (246620)
刘先杨 杨续亮
2016年高考天津理科压轴题简解的深度揭秘*
安徽省安庆市岳西县汤池中学 (246620)
刘先杨 杨续亮
2016年高考天津卷理科第20题为:
设函数f(x)=(x-1)3-ax-b,x∈R,其中a,b∈R.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若f(x)存在极值点x0,且f(x1)=f(x0),其中x1≠x0,求证:x1+2x0=3;
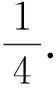
本文对试题的第三问作一探究,第(Ⅰ)(Ⅱ)问答案略.
一、参考答案的解法
(Ⅲ)证明:设g(x)在区间[0,2]上的最大值为M,max{x,y}表示x,y两数的最大值.下面分三种情况讨论:
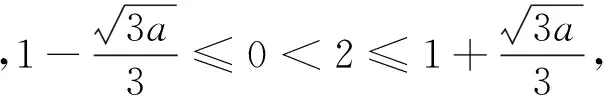
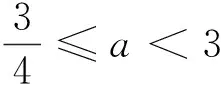
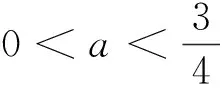
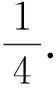
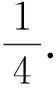
二、赋值法的简解
解法二:(Ⅰ)和(Ⅱ)同解法一.
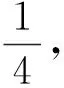
解法三:g(x)在区间[0,2]上的最大值为G,则
G≥g(0)=|f(0)|=|-1-b|,G≥g(2)
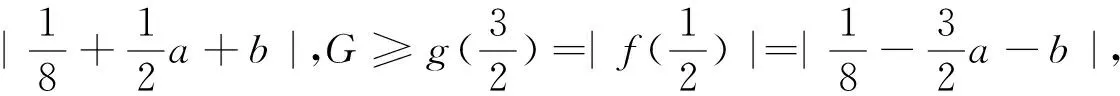
三、赋值法的质疑
我们来分析2010年全国高中数学联合竞赛一试第9题:
已知函数f(x)=ax3+bx2+cx+d(a≠0),当0≤x≤1时,|f′(x)|≤1,试求a的最大值.
参考答案给了两种解答方法,第一种解法是f′(x)=3ax2+2bx+c,由
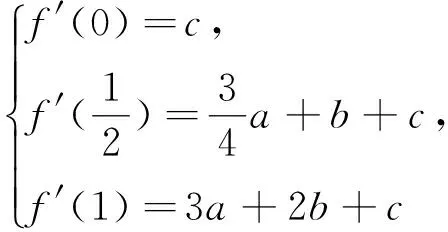
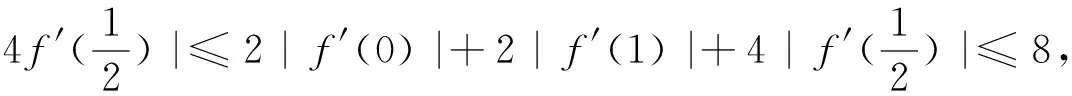
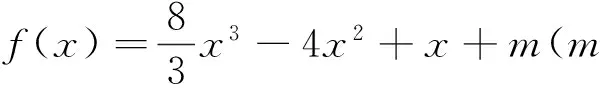
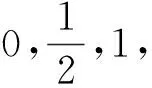
四、赋值的规律
通过分析可以得出一般的结论:
结论 一般地,已知函数f(x),当x∈[a,b]时,m≤f(x)≤n等价于m≤f(x)max≤n,m≤
f(x)min≤n同时f(x)max,f(x)min都是在区间的端点值和极值点处取得,故要确定f(x)的某些系数或者证明不等式,就可以用赋值法考虑给x赋那些值.
五、高考链接
(2015·浙江高考理科第18题)已知函数f(x)=x2+ax+b(a,b∈R),记M(a,b)是|f(x)|在区间[-1,1]上的最大值.
(1)证明:当|a|≥2时,M(a,b)≥2;
(2)当a,b满足M(a,b)≤2时,求|a|+|b|的最大值.
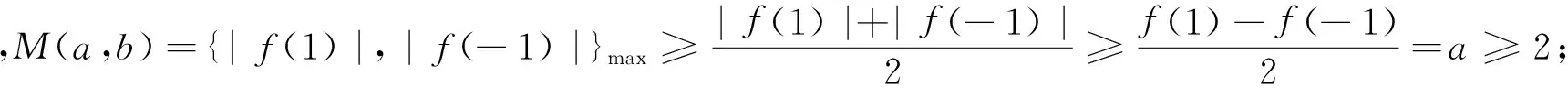
当a≤-2时,M(a,b)=
即当|a|≥2时,M(a,b)≥2.
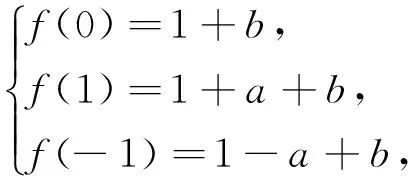
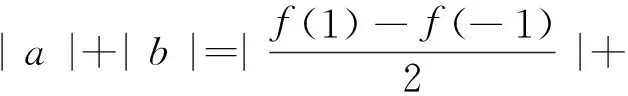
|f(1)+f(-1)|]+1=
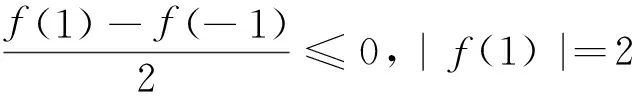
[1]2016年高考:数学试题创新解法赏析(续I)[J].中学数学教学参考.2016.8:56-56.
[2]丁云龙.2010年全国高中数学联合竞赛[J].中等数学.2010.12:24-28,45.
[3]张福俭,蒋红慧.一类赋值法赋值规律深度揭秘[J].数学通讯下半月(教师).2016.5.28-30.
*本文系安庆市教育科学规划课题“学生数学学习质疑能力的培养策略研究”(AJKT2015-82,主持人:杨续亮)的研究成果.

