数学教学应重视由特殊到一般的建构学习
江西师大数学与信息科学学院 (330027)
付奕玲*
数学教学应重视由特殊到一般的建构学习
江西师大数学与信息科学学院 (330027)
付奕玲*
1 引言
一般地,人们对特殊事物往往易于接受、理解,由特殊到一般是人们普遍的认识过程.同样的,学生数学学习过程也往往是在特殊条件下进行分析,然后再推广应用于相同属性的对象.这种从个别或特殊的事物所做的判断,再推广到同类事物的判断,即为从特殊到一般的推理.数学概念是建立在相关法则、公式及定理基础上的,所以要理解一个数学概念,就必须围绕这个概念逐步构建相应的概念网络,使概念之间形成网络节点,网络的结点越多、路径越丰富,概念理解相对就越深刻.数学定理是数学知识中的重要基础和工具,定理的证明和发现过程对培养学生的创新能力和逻辑思维具有不可替代的重要意义.数学学习中往往需要将把认知结构中已有特殊的概念和定理,与一般的概念和定理建立起合乎学生理解的逻辑关系,并努力形成实质性的联系,从而达到有意义的数学建构学习的目标.
2 案例
案例1 由函数关于原点对称推广到关于任意点对称
“数学科学特别展示了秩序、对称和极限,这些是美的最伟大的形式”.对称,是数学美的一种表现形式,这种对称美在函数知识内容里有充分的诠释.比如奇函数的定义为:对于函数f(x)的定义域D内任意一个x,如果都有f(-x)=-f(x),则称f(x)为奇函数.由定义可知奇函数图像关于原点对称.原点是一个特殊点,其本质特征是关于点的对称关系,如果将定义的特殊属性推广到一般条件下,最简单的就是关于任意点(a,b)的对称问题.
奇函数关于原点对称,从函数图像观察可知,就是函数中对应点的横坐标关于y轴对称,纵坐标关于x轴对称,验证关系式亦成立,由此猜想是否关于任意点(a,b)的对称也就是函数上的对应点横坐标关于x=a对称,纵坐标关于y=b对称.根据对称的性质,自变量关于x=a对称,设其中一点的横坐标为x,则另一个对称点的横坐标为-x+2a;对应点的因变量分别为f(x),f(-x+2a),其中一个自变量纵坐标为f(x),那么另一个关于y=b对称的对应点的自变量纵坐标的值应该是-f(-x+2a)+2b,即f(x)=-f(-x+2a)+2b,也可以变换为f(a+x)-b=-f(a-x)+b.这是分析和猜想的结果,要确定是否为此关系式,还需要经过验证.
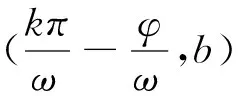
案例2 由勾股定理推广到余弦定理
勾股定理是数学内容中的“千年第一定理”,表示的是直角三角形斜边的平方等于两直角边的平方和,即c2=a2+b2.定理表示的是三角形边与边之间的关系,其中有一个特殊条件就是直角三角形,所以应该是边角之间的关系,自然地会猜想一般的三角形是否也存在类似的边角关系.因为特殊三角形的边角关系满足一般三角形的边角关系,所以一般三角形的边角关系式中不可能是在c2=a2+b2中的一项或几项中乘以某个数或式子,故一般三角形的边角关系式应该是在c2=a2+b2的基础上存在另外的项.
猜想 以其中一个角为30°的特殊直角三角形为例进行探索,如图1所示,∠C=90°,∠A=30°,c=2.
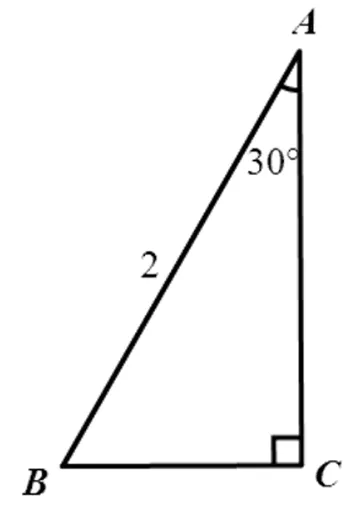
图1
猜想1c2=a2+b2+x(x表示未知项),当∠C=90°时,最后一项不存在,所以在未知项里面可能有cosC,即被求边的对应角的余弦值.
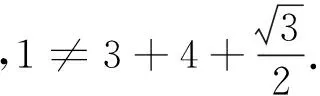
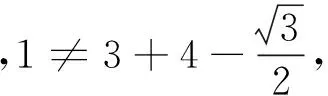
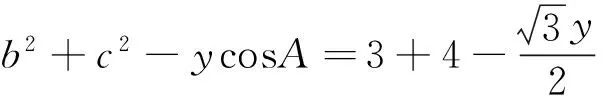
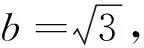

猜想7a2=b2+c2-c2bcosA,推理可知,在一般式中,b,c的地位应该是一致的,所以添加的一项中应该也只有一个c,所以z=2c更合理.
猜想8a2=b2+c2-2bccosA,如果猜想正确,即b2=a2+c2-2accosB也成立,将已知的边角的值代入最终猜想的一般式中,验算得出式子两边的值相等.
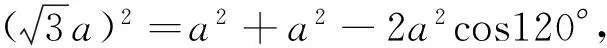
3.结语
由特殊到一般是数学建构学习的一种重要方式,这种学习方式要求教师在数学教学过程中应重视数学内容的特殊内涵分析、提炼,并作广泛迁移.教师不应该是把现成的结论教给学生,而是根据数学内容的发生发展过程,创设问题情境,充分利用各种方式方法,设计系列问题,增加辅助环节,并让学生通过大量的图形观察和实际问题的演算,使直观想象到发现猜想和归纳,最后进行结论的验证和理论证明,从而使学生亲历数学知识的建构过程,逐步掌握数学内容的本质方式和方法,提高学生学习兴趣和学习效率,真正发挥由特殊到一般的数学建构学习过程在数学教育中的育人价值.
*作者为2014级在读数学教育专业硕士研究生.

