变质量单自由度立方非线性振动系统动力学特性研究

徐　鹏

（辽宁省农业机械化研究所，沈阳 110161）

常系数微分方程广泛应用于物理学与工程学中系统的振动行为。虽然许多振动问题可以用这类方程进行充分描述，但是对于一般遇到的系统，需要采用带有时变参数的微分方程。Flores通过试验研究了一个线性变质量单自由度系统的振动特性。Nhleko在合并了两个通常用于描述带有可变参数的单自由度自由振动系统的独立方程之后，提出了一个一般形式上的控制方程。但以往文献很少涉及线性变质量单自由度立方非线性振动系统的动力学特性。

大多数的非线性微分方程没有精确的解析解，所以只能采用一些近似方法来解决，目前许多近似方法已经发展得很成熟。对于含有小参数的微分方程，近似解析方法包括Linstedt-Poincaré法、多重尺度法、平均法、Krylov-Bogoliubov-Mitropolsky法等；对于含有大参数的微分方程，近似解析方法包括修正的Linstedt-Poincaré法、谐波平衡法等。

根据拓扑学中的同伦，何吉欢提出了同伦摄动（HPM）方法，用以解决非线性问题。HPM方法的有效性和微分方程中是否存在小参数是没有关系的，该方法已经成功应用于许多非线性问题当中。

1　线性变质量单自由度立方非线性振动系统分析

本研究应用HPM求解线性变质量单自由度立方非线性振动系统的近似解，系统动力学方程为：

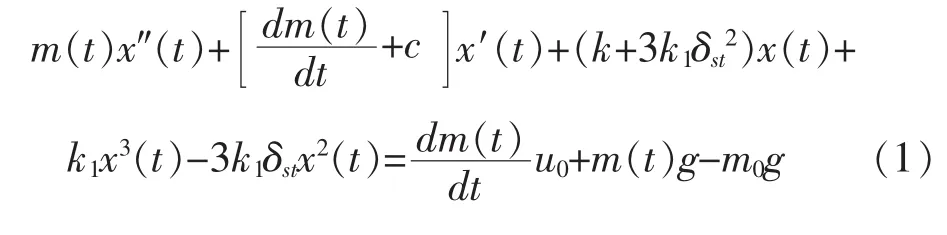
初始条件为：

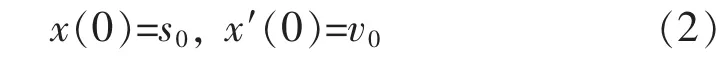
式中：x（t）为系统的位移响应；“′”为对时间 t的微分。

式中：m0和α均为实数；k为线形弹簧系数；k1为立方非线性弹簧系数，c为阻尼系数；δst为弹簧的静态变形。弹簧的静态变形可以由下面的公式解得：

线性变质量单自由度立方非线性振动系统如图1所示。

图1　变质量振子的力学模型Figure 1　Mechanical model of variable mass oscillator

2　求解过程

通过嵌入一个在［0，1］变化的参数 p，将变量x（t）转化为 X（t，p），这样方程（1）变为：

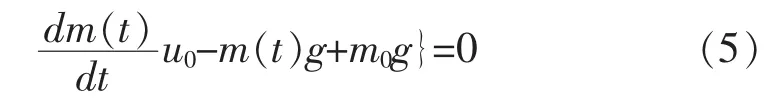
初始条件为：

式中：p 为同伦参数；x0（t）为方程（1）的初始近似解，且满足：

可以得到：

假设方程（5）的解为如下形式：

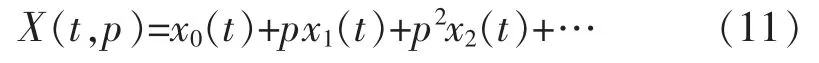
当 p＝1时，方程（1）的近似解为：

将公式（11）带入公式（5），并比较p的同次幂系数，可以得到：

由公式（7）得出 x0（t），然后带入公式（13）解得x1（t）。用相同的方法可以得到 x2（t）， x3（t）等。

3　各阶近似解

公式（7）表示一个单自由度变质量线性弹簧振子的动力学方程，为了获得初始解 x0（t），在公式（7）两边同时乘以 x0′（t），得到：

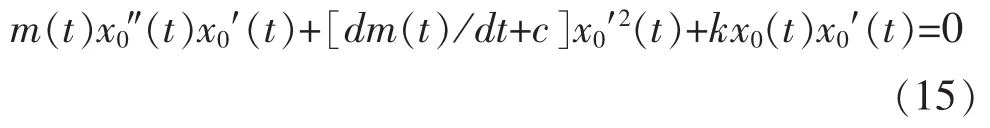
变质量线性弹簧振子的动能和势能可以写成：

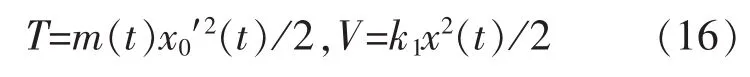
系统能量的微分为：

根据公式（15）和公式（17）可写为：

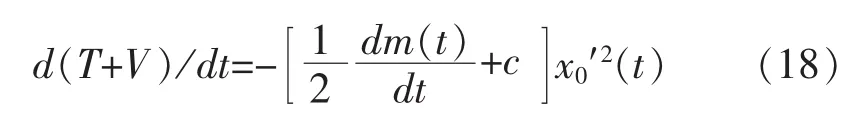
初始近似解 x0（t）表达为：

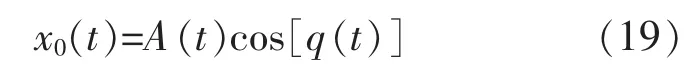
由于系统能量的变化仅仅是由质量变化引起的，所以：

x0′2（t）能够被一个振动周期内的平均速度代替：

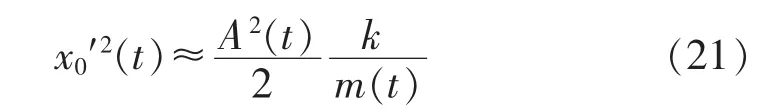
根据公式（18）、公式（20）和公式（21）可以得到：

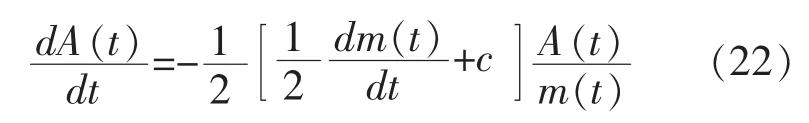
公式（22）的解为：

式中：A0为一个由初始条件决定的实数。

将公式（19）带入公式（7），可以得到：

将公式（23）带入公式（24），得到：

式中：α＝k/m0；b＝α2/16-c2/（4m02）。公式（25）的解为：

式中：θ为由初始条件决定的实数。根据初始条件，A0和θ可以解得：

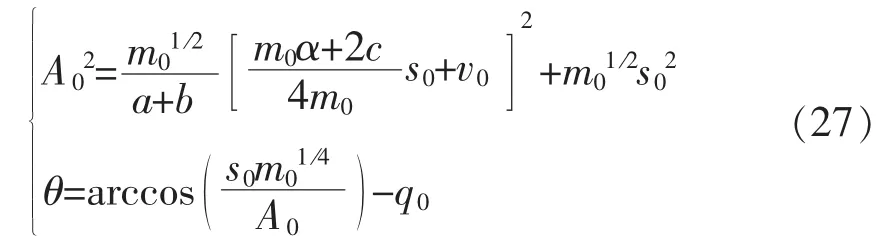
其中：

线性变质量系统的初始近似解为：

将公式（29）带入公式（13），可以得到系统的一阶近似解：

其中：

将公式（29）和公式（30）带入公式（14），可以得到系统的二阶近似解。在本研究中仅解到一阶近似解。

4　具体算例

为了说明上述方法的有效性，考虑m0＝1 kg，α＝0.01，c＝0.01 N·s/m，k＝2 500 N /m，u0＝1.0 m/s，s0＝1.0 m，v0＝1.0 m/s，g＝9.8 N/kg 的情况，假定 λ＝k1/k。 用上述方法得到的一阶近似解与由龙格库塔方法得到的数值解吻合的非常好，如图2所示 （图中：实线为HPM方法；带圈线为数值解）。

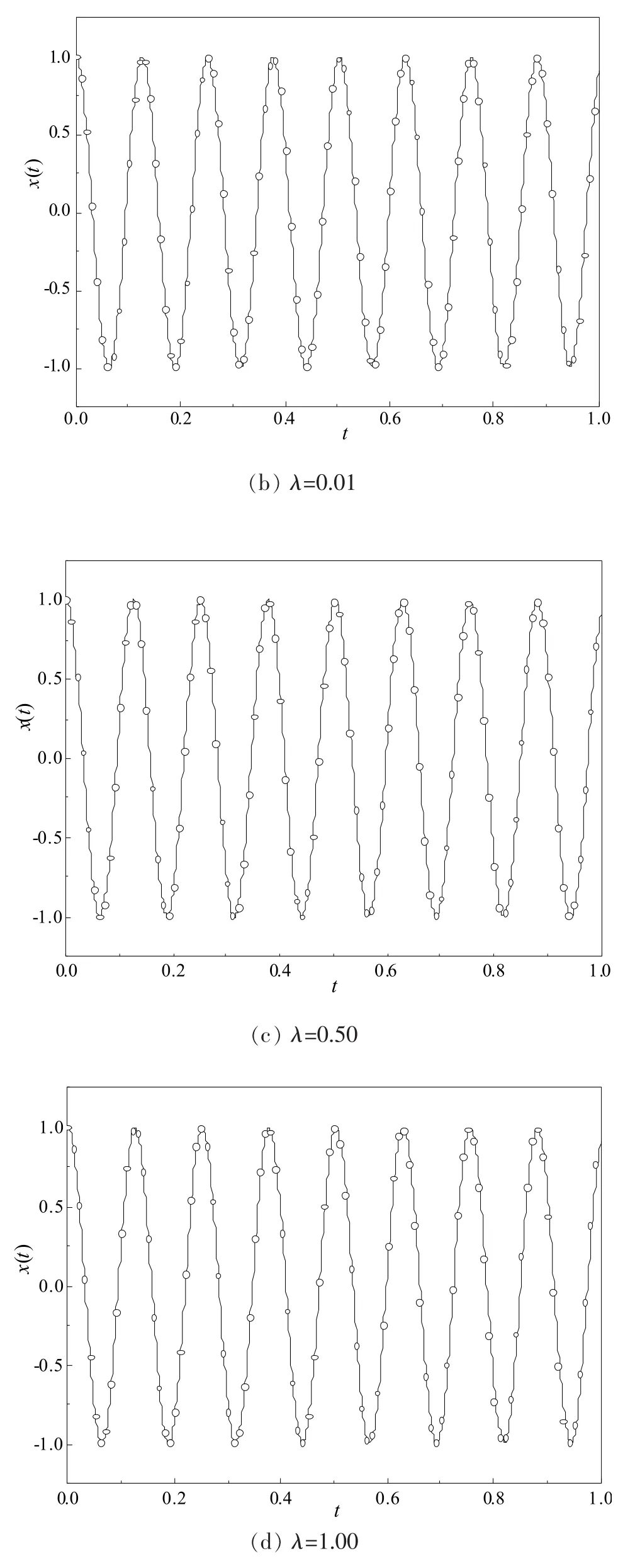
图2　不同λ值下，HPM方法的一阶近似解与数值解的比较Figure 2　The comparision of first approximation solution and arithmetic solution by HPMunder different λ value

不同α下相应的一阶近似解的相位图如图3所示（图中实线为HPM方法；带圈线为数值解）。

图3　不同α值下，HPM方法的一阶近似解相位图与数值解的比较Figure 3　The comparision of first approximation solution phase diagram and numerical solution by HPMunder different α value

5　结论

本研究应用HPM方法求得线性变质量单自由度立方非线性振动系统的近似解析解，并与数值解进行了比较，很明显地看到了HPM方法对更广泛的偏微分方程进行解析求解的有效性。

［1］NEWLAND，D.E..Mechanical vibration analysis and computation［M］.New York：Longman Science ＆ Technical，1989.

［2］TIMOSHENKO，S.Vibration problems in engineering［M］.London：Constable ＆ Company Ltd.，1937.

［3］NHLEKO S.，Free vibration states of an oscillator with a linear time-varying mass ［J］.Journal of Vibration and Acoustics，2009，131（5）：1-8.

［4］JOSE FLORES，GUILLERMO SOLOVEY，SALVADOR GIL.Variable mass oscillator ［J］.American Journal of Physics，2003，71（7）：721-725.

［5］P.J.MELVIN.On the construction of poincare-lindstedt solutions：the nonlinear oscillator equation ［J］.SIAMJournal on Applied Mathematics，1977，33（1）：161-194.

［6］A.H.NAYFEH.Perturbation Methods［M］.New York：John Wiley ＆ Sons，1973.

［7］G.S.LARIONOV，V.T.KHOANG.The method of averaging in nonlinear dynamical problems occurring in the theory of viscoelasticity［J］.Polymer Mechanics，1972，8（1）：31-35.

［8］T.KAKUTANI，N.SUGIMOTO.Krylov-bogoliubov-mitropolsky method for nonlinear wave modulation ［J］.Physics of Fluids，1974，17（8）：1 617-1 625.