层理性地层钻井稳定性分析模型

丁立钦，王志乔，3，王 瑜，刘宝林，吕建国

(1.中国地质大学〈北京〉工程技术学院，北京100083;2.国土资源部深部地质钻探技术重点实验室，北京100083; 3.国土资源部复杂条件钻采技术重点实验室，吉林长春130026)

钻探与钻井工程

层理性地层钻井稳定性分析模型

丁立钦1，2，王志乔1，2，3，王 瑜1，2，刘宝林1，2，吕建国1

(1.中国地质大学〈北京〉工程技术学院，北京100083;2.国土资源部深部地质钻探技术重点实验室，北京100083; 3.国土资源部复杂条件钻采技术重点实验室，吉林长春130026)

针对钻井工程常遇的层理性地层，以应力张量坐标转换关系和井孔应力集中方程为基础，引入弱面剪切滑动和岩体Mogi－Coulomb双强度准则，建立了分析层理性地层井壁稳定性的模型。对含层理弱面的典型油气储层中钻井的合理钻井液密度和安全钻井方向进行研究，结果表明:层理面的存在加剧了井壁围岩的破坏，且改变了围岩破坏的位置;水平井坍塌压力随着钻井方向变化而连续性变化，其在特定钻井方向取得最小坍塌压力;斜井取得最小坍塌压力的方位与层理面在空间中并不垂直，空间中关于主平面对称的斜井破裂压力相同;既可获得较大钻井液安全压力窗口又可取得较小坍塌压力的方向为优选钻井方向，在钻井液压力窗口变化大的倾向上钻井需严格控制钻井轨迹曲线。

层理;钻井液安全密度窗口;轨迹优化;井壁稳定性;模型

0 引言

井壁失稳是钻井工程中常遇的技术性难题，由井壁失稳造成的井壁垮塌、缩径、漏失等井下事故严重影响了油气资源勘采的施工效率和成本［1－2］。在钻井过程中井内原岩被钻井液取代，由此引发的井壁失稳问题一般包括井壁坍塌和井壁破裂两个方面:当钻井液密度较低时井壁围岩应力集中明显，围岩被压碎引起井壁坍塌;在过高的钻井液压力下围岩局部被拉裂，由此产生循环损失进而引起围岩强度降低等问题。因此钻井施工中确定井眼坍塌压力与破裂压力是维持井壁稳定的关键［3］。随着钻井工程逐渐向深部发展，钻遇岩层的复杂程度增加，而在油气资源广泛分布的储层区岩石的层理十分发育，由此引起岩石强度特征发生变化，进而增加了岩层中钻井稳定分析的复杂性。理论与实践证明，当井周围岩中存在层理软弱面时，多数岩体会沿层理面优先破坏［4－12］，因此研究井壁稳定问题需要充分考虑地层软弱面的影响。

为解决层理性地层井壁失稳问题，国内外学者进行了许多相关研究。Jaeger［4］和Chenevert［5］首先讨论了含软弱面岩石的强度特征，发现随着弱面角度变化岩石会发生不同形式的破坏;Aadnoy［6］建立了基于Mohr－Coulomb强度准则的单弱面强度各向异性井壁稳定模型;Okland［7］等利用厚壁圆筒实验验证了不同角度弱面存在对井壁围岩强度的弱化作用;金衍、刘向君［8－9］等分析了不同弱面产状对直井及斜井井壁稳定性的影响;Chen［10］、Lee［11］、马天寿［12］等分别用数值方法和半解析方法研究了岩体中的层理、裂缝对安全钻井钻井液密度设计的影响。以上工作多建立在传统Mohr－Coulomb准则基础之上，未结合岩体、弱面的双强度准则综合考虑并分析其差异性，同时也有必要具体研究水平井、斜井安全施工设计的方法、有效规避风险。为此，笔者建立了层理性地层全方位钻井综合分析井眼稳定性的模型，利用弱面与岩体双强度准则对围岩破坏进行控制，给出了计算井眼坍塌压力与破裂压力的方法与公式，并从钻井设计的角度对水平井及斜井合理钻井液密度选取与安全轨迹规划给出了具体建议。

1 含层理弱面岩体的强度弱化特征

围岩中含层理面时强度会降低，当应力方向与弱面夹角不同时围岩的破坏形式与强度也不相同。为验证含层理软弱面岩石的强度弱化特征，并为进一步的模型计算建立实验基础，选取含不同倾角(弱化面与加载方向夹角 ω分别取0°、30°、45°、60°、90°)软弱面的三组板岩岩样做单轴加载实验，加载速率为0.5 MPa/s。岩样破坏情况如图1所示，可以看到当加载方向与弱面夹角在30°～60°之间时岩样主要沿软弱面发生贯穿性剪切滑动破坏，而当加载方向与弱面夹角为0°或90°时岩样呈现出整体劈裂破坏与局部剪切破坏共存的破坏形式。

图1 单轴压缩实验中含不同角度层理面岩样的破坏情况

将赵文瑞［13－16］等选用不同种类的各向异性岩样进行单轴压缩的实验结果与本文实验结果(3组实验结果均值)表示在图2中。综合分析以上5种实验结果发现:尽管不同种类岩石单轴抗压强度(UCS)有所区别，但对于某种特定岩样的UCS值随弱面角度改变而变化的规律趋于一致性;实验结果均显示当加载方向平行或垂直于软弱面时(ω=0°或90°)，获得的UCS值最高，而当加载方向与弱面夹角取30°时岩样单轴加载强度最低;同时注意到除含灰页岩外其它岩石的UCS值随弱面倾角改变而变化很大，极值之差最高达94 MPa，说明特定产状的层理弱面对多数岩石的强度弱化作用显著。因此，当层理软弱面与加载方向具有特定的角度关系时，岩石中软弱面的剪切滑动是造成岩石破坏的主因，因此软弱面的稳定性可能会成为制约地下钻井工程安全稳定性的关键因素。

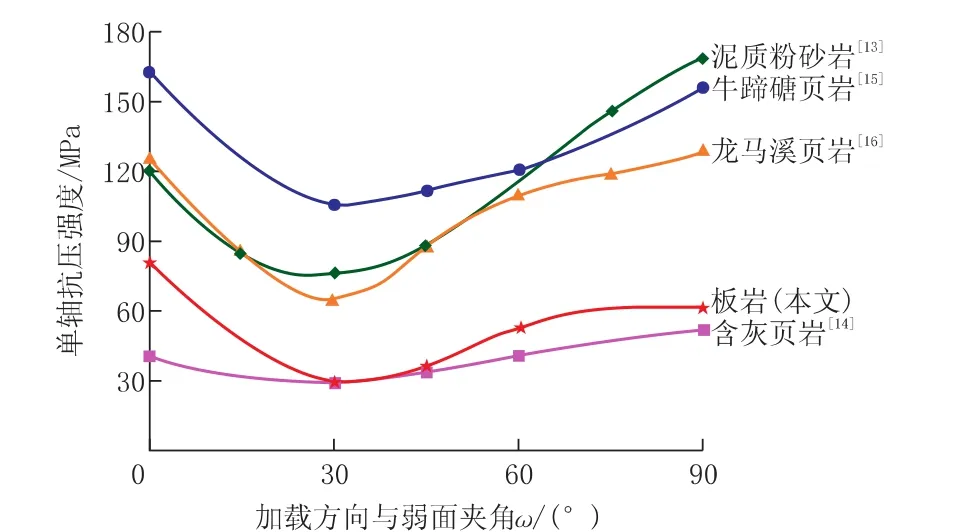
图2 本文实验及文献中各向异性岩样的单轴抗压强度

2 建立层理性地层井壁稳定力学模型

2.1 地应力坐标系、井筒坐标系与井壁应力集中

在实际钻井工程中，地应力方向、钻井轨迹、岩体层理面方位的组合关系具有任意性，需要建立井筒坐标系、层理弱面坐标系与地应力坐标系之间的应力转换关系，从而便于进一步的井壁围岩稳定性判断。地下深部岩体通常受到一个垂向上覆压力(σv)和两个水平主应力(σH≥σh)作用(见图3)，

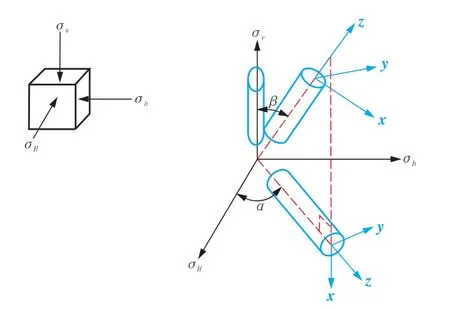
图3 井筒坐标系与地应力坐标系

某一地应力水平可表示为地应力坐标系下的张量形式:

式中:［σe］——地应力坐标系下的初始地应力张量，MPa。

为更有效地开发地下能源，水平井及斜井施工在钻井工程中应用越来越广泛，建立任意方向斜井的井筒坐标系如图3所示。任意斜井井筒坐标系由初始位置(x、y、z轴方向分别沿 σH、σh、σv方向，即垂直井孔)旋转到图3所示位置需要经过两个过程:首先以初始竖直z轴为中心将其旋转α角(倾向)，然后以y轴为中心将其旋转β角(倾角)，即可得到当前斜井井筒坐标系。水平井直角坐标系获得方法与斜井相类似，此时倾角β=90°(见图3)。由几何关系可知，地应力坐标系下应力张量［σe］向斜井井筒直角坐标系下转换可采用如下转换矩阵:

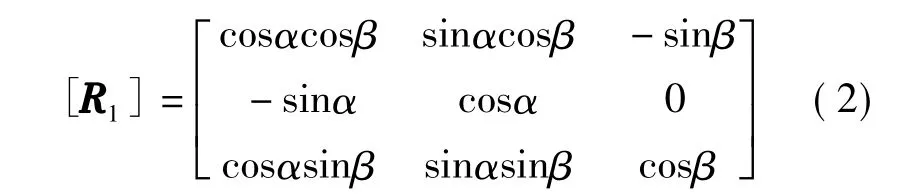
式中:α——井筒的倾向;β——倾角。

由此得到井筒直角坐标系下地应力张量［σb］为:

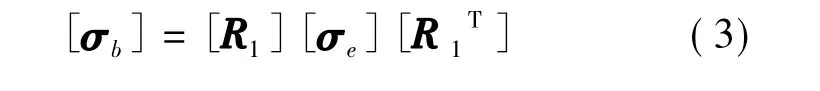
即:

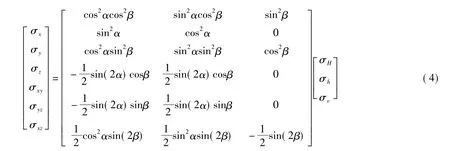
式中:σij——为［σb］的各分量形式，MPa，其中i，j∈(x，y，z)。

在钻孔形成过程中井内岩石被取出，在［σb］作用下井壁围岩产生应力集中效果(见图4)，在线弹性假定下Bradley［17］建立了不考虑流体渗透影响的井壁围岩应力集中方程:

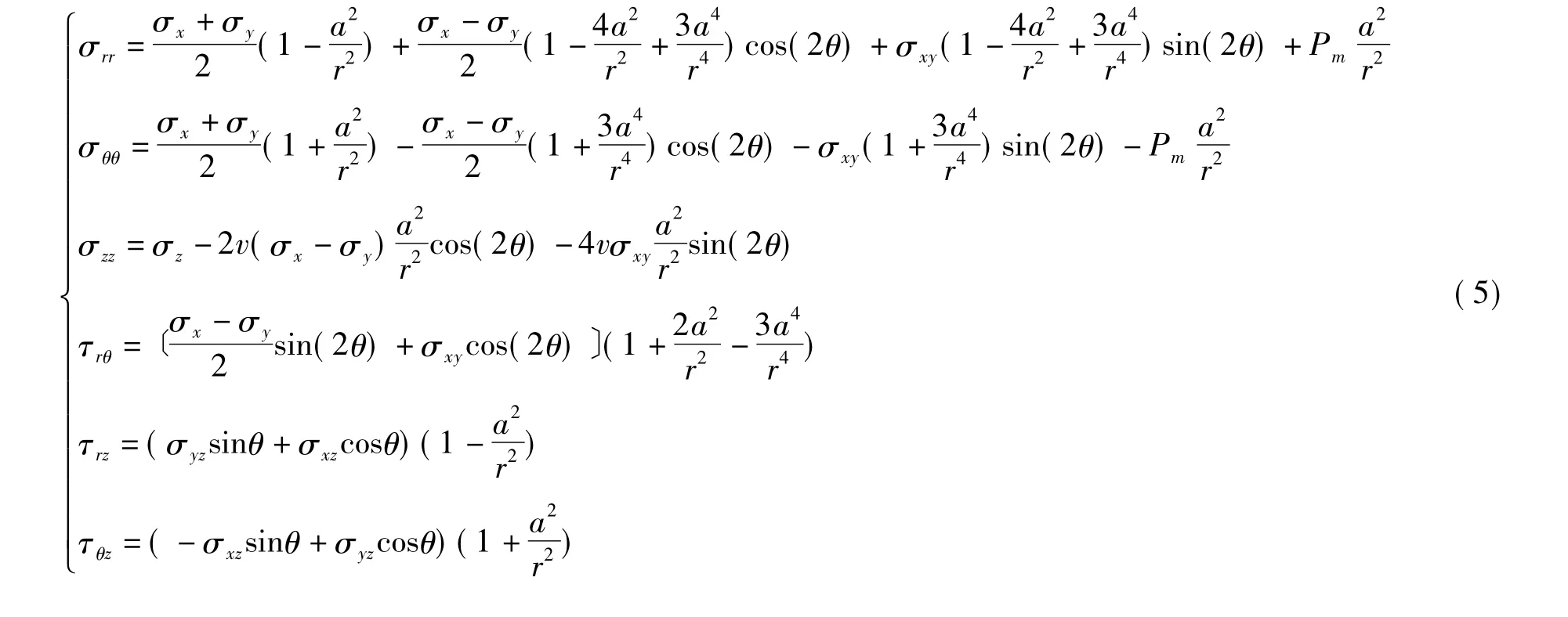
式中:σij——为井筒柱坐标系下集中应力张量［σc］的各分量形式，MPa，其中i，j∈(r，θ，z);a——孔半径，m;r——井周一点到井眼中心轴线的距离，m; θ——井壁上一点由x轴方向逆时针转过的角度(见图4)，(°);Pm——井内钻井液液柱压力，MPa; v——泊松比。

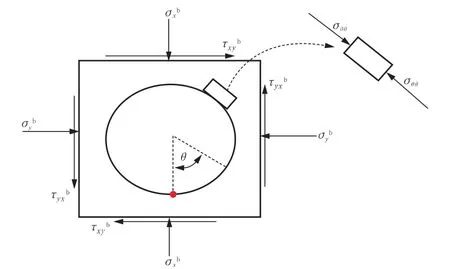
图4 井壁围岩应力集中情况

在井壁处(r=a)，式(5)可简化为:

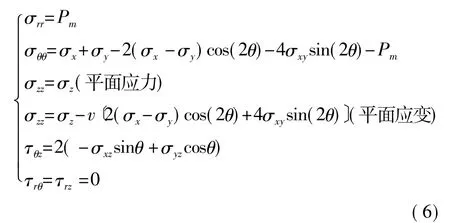
Zhang等［18］通过数值计算证明泊松比对井壁应力及破坏情况影响较小，为简化计算可忽略其影响(平面应力)。井壁围岩集中应力的主应力值可通过对式(6)所求［σc］求其特征值得到:

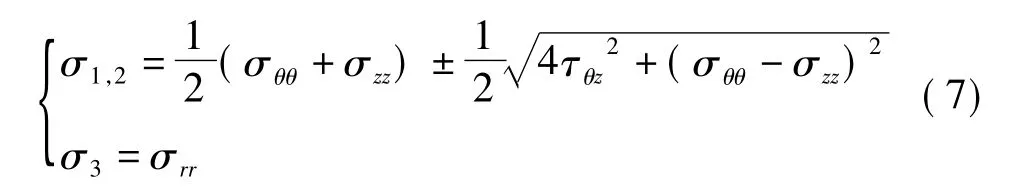
式中:σ1、σ2、σ3——围岩应力中的各主应力值(随井内压力变化其大小关系不确定)，MPa。

2.2 层理弱面坐标系

沉积岩体中通常发育一组平行结构层理面，当钻井工程钻遇此类岩体时需考虑层理面对井壁围岩强度的弱化作用，为充分考虑层理面方向与钻井方向的任意组合关系，并进一步进行井壁稳定性分析，需要首先建立层理弱面直角坐标系。

假设某一层理位于图5中B位置，为其建立图示oxyz坐标系，其中ox轴沿该层理弱面法线方向，oy、oz轴位于弱面内且oy轴方向与该弱面走向一致(即oy轴在水平面内，方向与弱面走向重合)。该弱面由初始A位置(走向沿σh方向、倾向沿σH方向、倾角90°的竖直面，弱面坐标系与地应力坐标系重合)旋转到任意B位置需要2个过程:首先将弱面A绕σv轴旋转δ角，然后绕oy轴旋转φ角，由此便得到走向沿oy方向、倾向沿ox'方向、倾角90°－φ的B位置任意方向层理弱面。由几何关系得层理弱面坐标系oxyz与地应力坐标系之间的应力张量转换矩阵为:

式中:δ——弱面的倾向，φ——弱面倾角的余角。

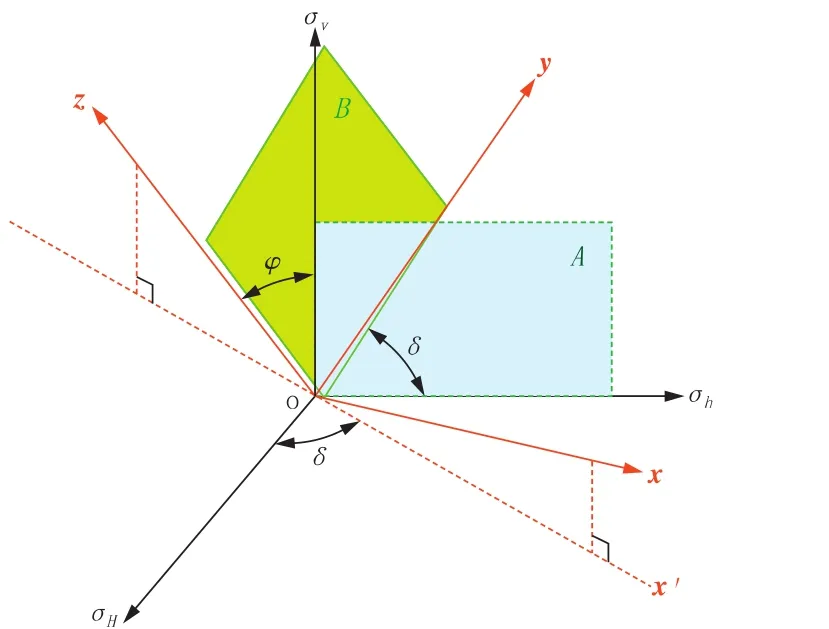
图5 地应力坐标系与层理弱面坐标系

为分析井壁围岩中层理面的稳定性，需要将式(5)或式(6)计算的井壁围岩集中应力张量［σc］转换到弱面坐标系oxyz下。柱坐标系下［σc］与其对应的直角坐标系应力张量的相互转换矩阵为:

式中:θ——直角坐标系由x轴方向逆时针转过的角度，(°)。

因此，式(5)或式(6)求得的［σc］向弱面坐标系oxyz下转换关系式如下:

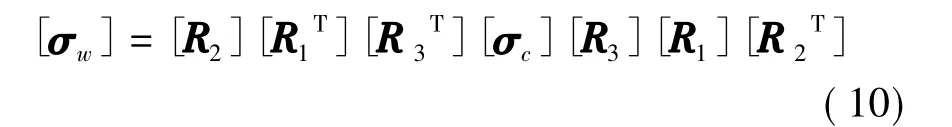
式中:［σw］——围岩集中应力在层理弱面坐标系下的张量表示，MPa。

综合应用式(3)、(4)、(5)、(6)、(10)即可计算在一定水平的地应力作用下，由于钻井开孔施工引发的应力集中效果在某一层理弱面坐标系下作用的应力张量。

2.3 层理弱面与完整岩体强度准则

在求得层理弱面坐标系(图5中oxyz坐标系)下应力张量［σw］后，根据柯西公式［19］可以方便地求得作用在该弱面内的剪应力τ和垂直于弱面作用的法向应力σn:

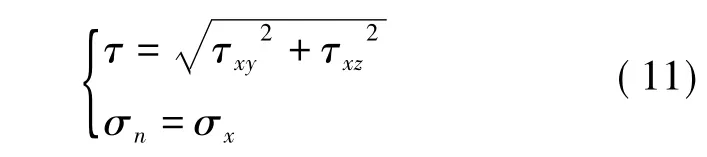
式中:τxy、τxz、σx——分别为［σw］中对应的各应力分量，MPa。

岩体中所含弱面的稳定性由Jaeger和Cook［20］给出的单弱面岩体剪切滑动准则判断:

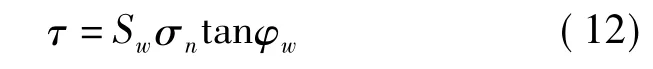
式中:Sw——围岩层理面所具有的粘聚力，MPa; φw——围岩层理面所具有的内摩擦角，(°)。

对于钻井常遇无弱面完整硬脆性岩体，Al－Ajmi等［21］通过真三轴实验证明Mogi－Coulomb准则具有较好的适用性。Mogi－Coulomb准则在常规三轴应力下(σ2=σ3)可退化为Mhor－Coulomb准则，其可视为Mohr－Coulomb准则在真三轴应力条件下的推广，因此理论应用范围更加广泛。Mogi－Coulomb准则形式如下:

各参数表达式如下:

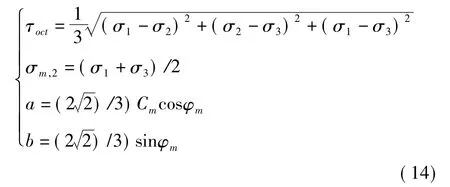
式中:σ1、σ2、σ3——式(7)所求围岩主应力;Cm——无弱面完整岩体的粘聚力，MPa;φm——无弱面完整岩体的内摩擦角，(°)。

工程上为测定Cm、φm值只需对井下具有代表性的完整岩体取样，并在室内做常规三轴实验或变角剪切实验即可。而为获得Sw及φw值，可取井下含层理面的岩样在一定围压下进行三轴实验，根据图2所示实验结果，岩样层理面与轴向加载方向的夹角宜选为30°左右，因为在此情况下岩样易发生贯穿层理的剪切滑动破坏，由此获得的强度参数值与层理面真实值较为接近。

2.4 坍塌压力与破裂压力计算

在给定井斜角(α、β)及层理面方位(δ、φ)条件下，井眼坍塌压力Pwc可利用式(12)或式(13)计算(考虑有效应力作用)。为提高计算效率，可借助编程软件利用迭代法计算井壁上不同点(考虑对称性，井周角θ=k，k的取值间隔固定，如k=0∶0.1∶180)维持稳定需要的最小钻井液压力值，最终Pwc等于井壁各点求得钻井液压力值中的最小值，这样便可保证井壁上各点均不发生坍塌。

井内钻井液压力过高时容易发生井壁破裂现象，此时钻井液随裂缝进入地层弱化围岩强度，进而引发多种井内事故。一般认为井壁发生破裂是由于井内钻井液压力过大，导致围岩中最小有效应力超过了岩石的抗拉强度(此时Pm=σr＞σ1＞σ2)，即:

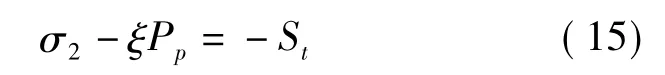
式中:ξ——比奥系数;Pp——孔隙压力，MPa;St——岩石抗拉强度绝对值，MPa。

将式(6)、式(7)代入式(15)，整理后可得到破裂压力Pwf的解析表达式:

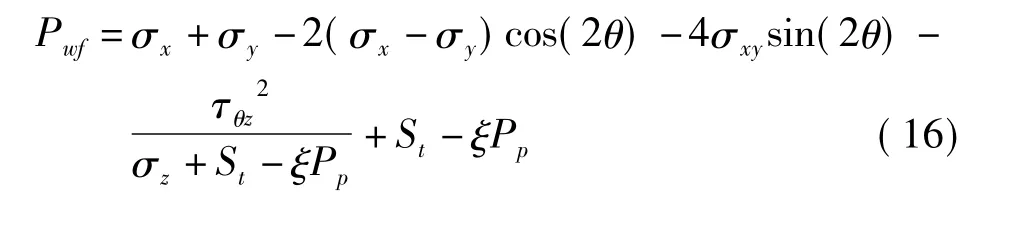
3 层理性地层水平井及斜井井壁稳定性分析

3.1 层理弱面加剧井壁围岩破坏

为了研究在层理弱面影响下的井壁围岩破坏特征，采用计算机软件编制了上文中介绍的分析井壁稳定性的计算程序，并根据油气产区地下岩体的一般特征假设计算所需要的地层基本参数为:深度3240 m，上覆地应力梯度23.0 MPa/km，最大水平地应力梯度26.5 MPa/km，最小水平地应力梯度18.7 MPa/km，孔半径0.15 m，泊松比v=0.3，比奥系数ξ =1.0，岩体粘聚力Cm=27.7 MPa，岩体内摩擦角φm=31.6°，层理面粘聚力Sw=7.2 MPa，层理面内摩擦角φw=20.1°，层理面倾向/倾角为60°/30°，选取地层为走滑断层地应力机制(σH＞σv＞σh)。

在工程钻遇上述层理性沉积岩体(层理面倾向/倾角为:60°/30°)的情况下，选用井内钻井液密度为1.0 g/cm3(相当于水)，分别计算考虑层理面与不考虑层理面影响时，沿最小水平主应力方向钻进水平井时的井壁围岩破坏情况如图6所示。从图中可以看出，考虑层理面影响的井壁围岩破坏严重，最大钻孔扩径达140 mm(相当于孔半径)，且井壁上多处破坏向纵深发展，其贯通后可能引发更为严重的井壁失稳问题;而不考虑层理面影响的井壁围岩在井内注水施工的情况下基本不会发生破坏。由此可以看出在钻井工程中，若地层岩体中存在一定角度的倾斜层理面，则由钻井开孔引起的应力集中导致的孔壁围岩沿层理弱面的剪切滑动是引发孔壁不稳定问题的主因，在钻井稳定性分析中应引起足够的重视。

图6 井壁围岩破坏情况

图7 为沿最小水平主应力方向钻进时的井壁围岩集中应力分布情况。可以看到即使在井内注水的情况下，环向应力σθ的极值仍明显高于地应力水平，井壁应力集中效果明显;同时发现σθ(同σz)取得极值点的位置(θ=0°，180°)与图6(b)所示井壁破坏中心位置相同，这说明钻孔产生集中应力与不考虑弱面影响的围岩破坏情况具有较好的一致性，也正是这种应力集中效果导致了井壁围岩被压碎。而对比图6(a)可发现层理面的存在明显改变了孔壁的破坏位置和破坏区域面积，使得孔壁出现“四叶片”状破坏区域且破坏向纵深发展。

3.2 水平钻井方向优化

图8为计算沿最小水平主应力方向“干孔”(井内无钻井液)钻进时，井壁集中应力在围岩中θ= 90°处随径向距离增加而变化的情况。可以看到:环向应力σθ、径向应力σr和轴向应力σz的数值在距井孔一定远处依次趋近于有效垂向地应力、有效最大水平地应力和有效最小水平地应力的大小;环向应力σθ在井壁处(r=0.15)取得极值(约为远场有效垂向地应力值的3倍)，应力集中效果最为明显，因此钻井施工中选用的钻井液密度若能保证井壁不坍塌则围岩内部就不会发生坍塌破坏，这样通过计算井壁上环向各点维持稳定需要的钻井液密度并取其最大值即为井眼坍塌压力。

图7 井壁集中应力分布情况

图8 围岩一点(θ=90°)应力随径距变化情况

将3.1节中地层基础参数值代入模型计算程序，考虑层理面存在的情况下计算水平井沿不同方向(由最大水平地应力方向开始，间隔为10°旋转)钻进时的井眼坍塌压力结果如图9所示。图9中的不规则包络线为井壁上环向各点(θ=0°～360°)压缩破坏时的临界钻井液密度，可以看出:当水平井倾向(α角)在0°～50°和120°～180°时，井壁上各点临界破坏钻井液密度包络线随水平井方向改变而产生有规律的连续性旋转变化;当α角在60°～110°时，包络线随水平井方向改变变化不大;井眼坍塌压力会随着水平井方向的连续变化而发生连续性变化。

当井眼坍塌压力较低时，维持井壁稳定需要的允许钻井液密度也较低，此时可在保证钻井安全的前提下适当调低钻井液密度来提高钻井施工的经济效益。将不同方向水平钻井的井眼坍塌压力值表示在图10中，从图中可以看到当水平井方向与最大水平主应力方向夹角为0°～30°和150°～180°时井眼坍塌压力值较小，在以上方向钻进水平井的安全性较高且能取得较好的经济效益;而在水平井与最大主应力方向夹角为70°～130°时发生井眼坍塌事故的风险较高、经济性较差，在工程规划中应避免此类方向钻井设计。

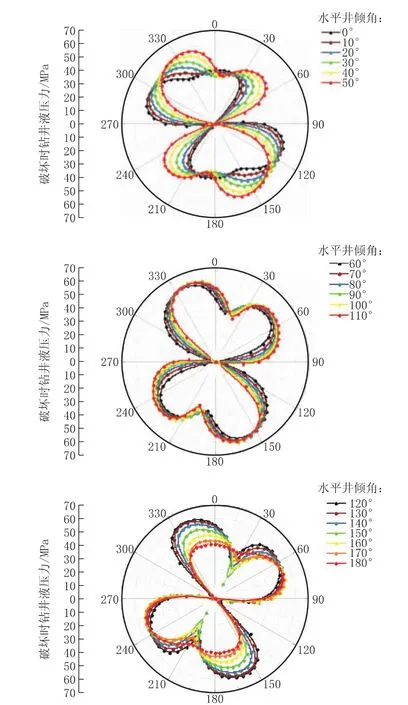
图9 不同方向水平钻进井壁上各点破坏时的钻井液压力

3.3 斜井轨迹优化与钻井液安全密度窗口

钻井液柱在井筒内产生的压力过小不能有效平衡井壁围岩的应力集中效果，会引起井眼扩径、坍塌、卡钻等事故，而当井内液柱压力过大时，井壁围岩集中应力被过分抵消而产生张拉应力，因岩石拉断产生的井壁破裂会使得钻井液渗入地层降低围岩强度，也会导致井壁失稳问题，井壁坍塌压力与破裂压力可采用2.4节中的方法进行计算。对于大斜度井而言，其井眼方位变化大，在层理弱面影响下，钻井轨迹的微小变化可能会影响对其稳定性的判断，因此需要在全方位上计算维持井壁稳定需要的钻井液安全压力。

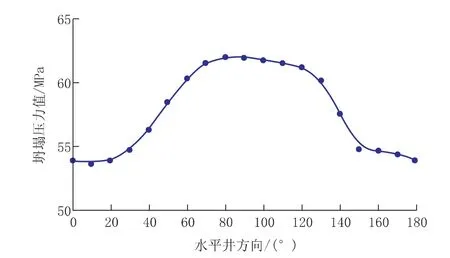
图10 不同水平钻井方向的井眼坍塌压力值

仍假设钻遇地层存在3.1节中层理弱面，计算在地应力坐标系下所有方向上钻进时维持井壁稳定需要的坍塌压力值如图11(a)、(b)所示(图中环向坐标代表井筒倾向、径向坐标代表井筒倾角)。图11(a)为式(12)的计算结果，其仅考虑了围岩层理面的强度破坏;图11(b)为式(12)与式(13)计算结果的叠加，其不仅考虑了围岩层理面的破坏，也考虑了完整岩体的强度破坏。由于在应力方向与弱面方向存在特定角度关系时弱面并不会发生剪切滑动(例如两者为垂直关系)，此时应利用岩体的Mogi－Coulomb破坏准则来给出围岩压剪强度界限，因此图11(b)的计算结果与实际情况更为相符。

分析图11(b)发现:在钻孔方向取30°/40°(倾向/倾角)左右方位区间时维持井壁稳定的坍塌压力值最小，该方位可作为降低工程预算成本时的优选方向;取得最小坍塌压力值的钻井方向在空间中并不垂直于层理面，这是由于其不仅与地层弱面有关还会受到局部地应力水平的影响，因此通过经验性的垂直关系来优选钻井方向的方法并不可靠;当倾向在60°～130°、240°～310°区间并采取高倾角钻孔施工时维持井壁稳定的坍塌压力值较高，在此类方向设计钻井应当慎重。

计算在所有井孔方向上的井壁破裂压力如图11(c)所示，因为考虑天然缺陷存在而忽略岩体拉伸强度(St=0)，可以看到井壁破裂压力并不受层理弱面存在的影响。同时可以看到井壁破裂压力值关于0°～180°轴、90°～270°轴(即最大、最小水平主应力方向轴)对称，这是因为当空间中井筒方向关于主平面对称时，井壁围岩应力也对称，故而井壁集中应力的极值也相同。

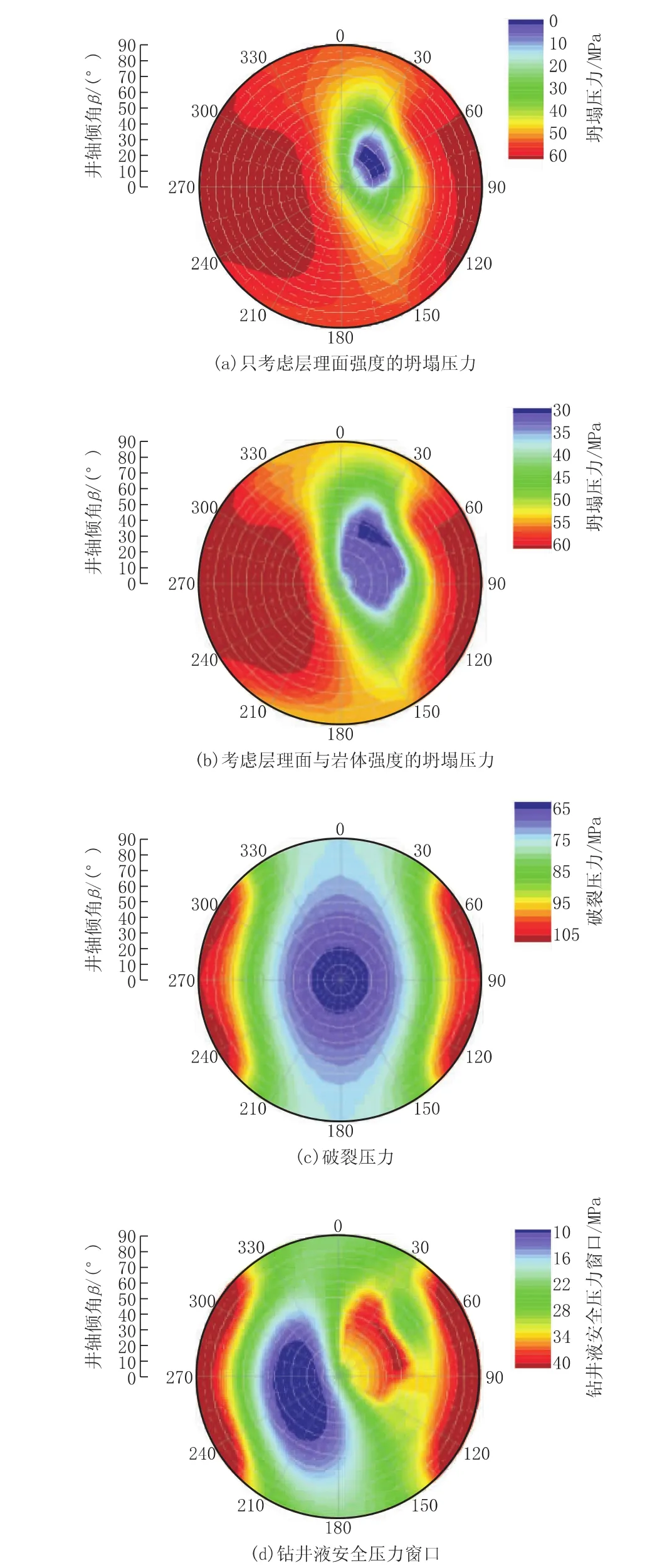
图11 全方位钻井的坍塌压力、破裂压力与允许钻井液压力窗口

在某一方向钻进的井壁破裂压力与坍塌压力之差即为该方向钻井的钻井液安全压力窗口，理论上窗口越大越有利于安全钻进，小窗口在一定干扰下容易丧失稳定性。图11(d)所示为计算得到全方位钻井的钻井液安全压力窗口，可以看到窗口最大出现在倾向45°～135°及225°～315°的近水平井位置和倾向/倾角为60°/40°附近位置处，而涉及到钻井安全及经济效益的双重考虑，取斜井倾向/倾角为60°/40°钻进是钻井设计的最优方向。在倾向255° ±60°、倾角30°±15°的斜井方向为最危险的钻井方向，一定程度的施工干扰可能会引发井壁失稳事故，此类钻井方向在施工设计时应当予以规避。同时注意到，在井眼倾向为225°～315°时，随着井眼倾角变化钻井液安全压力窗口变化幅度大，甚至由最大窗口向最小窗口过渡，因此在该倾向上进行斜井钻进时应尤其注意钻井轨迹控制。

4 结论

(1)通过室内实验及文献数据资料的对比，分析了含层理弱面不同种类岩石的强度弱化特征，结果表明含特定倾角弱面的岩石在加载时强度会明显降低，当加载方向与弱面夹角为30°时岩石强度最低。

(2)以不同坐标系下的应力张量转变关系和地层钻孔应力集中方程为依据，结合弱面剪切滑动准则和岩体Mogi－Coulomb强度准则建立了分析层理性地层井壁稳定性的模型，介绍了计算井眼坍塌压力和破裂压力的方法并给出了解析公式。

(3)计算分析了层理性地层水平井及斜井的安全钻井方向及合理钻井液密度，结果表明:层理面的存在明显加剧了井壁围岩的破坏，且改变了围岩破坏的位置;水平井坍塌压力随着钻井方向变化而连续性变化，在特定方向处取得最小坍塌压力;斜井取得最小坍塌压力的方位与层理面在空间中并不垂直，空间中关于主平面对称的斜井破裂压力相同;既可获得较大钻井液安全压力窗口又可取得较小坍塌压力的方向为优选钻井方向，在钻井液压力窗口变化大的倾向上钻井时需严格控制钻井轨迹曲线。

［1］陈勉，金衍，张广清.石油工程岩石力学［M］.北京:科学出版社，2008.

［2］吴纪修，张永勤，梁健，等.羌塘盆地天然气水合物钻探试验井工程井壁稳定性分析［J］.探矿工程(岩土钻掘工程)，2014，41 (6):8－13.

［3］Zoback M.Reservoir Geomechanics［M］.Cambridge University Press，2007.

［4］Jaeger J C.Shear Failure of anisotropic rocks［J］.Geological Magazine，1960，97(1):65－72.

［5］Chenevert M E.The deformation-failure characteristics of laminated sedimentary rocks［J］.Texas:University of Texas Press，1964: 87－123.

［6］Aadnoy B S.Modeling of the stability of highly inclined boreholes in anisotropic rock formations［J］.Society of Petroleum Engineers Drilling Engineering，1988，3(3):259－268.

［7］Okland D，Cook J M.Bedding-related borehole instability in highangle wells［C］//SPE/ISRM Rock Mechanics in Petroleum Engineering.Trondheim，1998，413－422.

［8］金衍，陈勉，柳贡慧，等.弱面地层斜井井壁稳定性分析［J］.石油大学学报(自然科学版)，1999，23(4):46－48.

［9］刘向君，陈一健，肖勇.岩石软弱面产状对井壁稳定性的影响［J］.西南石油学院学报，2001，23(6):12－14.

［10］ChenX，Tan C P，Detournay C.A study on wellbore stability in fractured rock masses with impact of mud infiltration［J］.Journal of Petroleum Science and Engineering，2003，38(3/4):145－ 154.

［11］Lee H，Ong S H，Azeemuddin M，et al.A wellbore stability model for formations with anisotropic rock strengths［J］.Journal of Petroleum Science and Engineering，2012，96/97:109－119.

［12］马天寿，陈平.层理页岩水平井井周剪切失稳区域预测方法［J］.石油钻探技术，2014，42(5):26－36.

［13］赵文瑞.泥质粉砂岩各向异性强度特征［J］.岩土工程学报，1984，6(1):32－37.

［14］李正川.岩石各向异性的单轴压缩试验研究［J］.铁道科学与工程学报，2008，5(3):69－72.

［15］陈天宇，冯夏庭，张希巍，等.黑色页岩力学特性及各向异性特性试验研究［J］.岩石力学与工程学报，2014，33(9):1772－1779.

［16］侯振坤，杨春和，郭印同，等.单轴压缩下龙马溪组页岩各向异性特征研究［J］.岩土力学，2015，36(9):2541－2550.

［17］Bradley W B.Failure of inclined boreholes［J］.Journal of Energy Resources Technology，1979，101(4):232－239.

［18］Zhang W D，Gao J J，Lan K，et al.Analysis of borehole collapse and fracture initiation positions and drilling trajectory optimization［J］.Journal of Petroleum Science and Engineering，2014，129 (5):29－39.

［19］Goodman R E.Introduction to rock mechanics，2nd Edition［M］.New York:John Wiley and Sons，1989:396－402.

［20］Jaeger J C，Cook N G W，Zimmerman R W.Fundamentals of rock mechanics，4nd Edition［M］.Chicester:John Wiley and Sons Ltd，2007:65－79.

［21］Al-Ajmi A M，Zimmerman R W.Stability analysis of vertical boreholes using the Mogi－Coulomb failure criterion［J］.International Journal of Rock Mechanics and Mining Sciences，2006，43 (8):1200－1211.

Analysis Model of Borehole Stability in Bedding Formations

/DING Li-Qin1，2，WANG Zhi-Qiao1，2，3，WANG Yu1，2，LIU Bao-Lin1，2，LU¨Jian-Guo1(1.School of Engineering and Technology，China University of Geosciences，Beijing 100083，China;2.Key Lab on Deep Geo-drilling Technology of the Ministry of Land and Resources，China University of Geosciences，Beijing 100083，China;3.Key Lab of Drilling and Exploitation Technology in Complex Conditions，Jilin University，Changchun Jilin 130026，China)

Bedding formations are often encountered in drilling operations.On the basis of the stress tensor coordinate transforming relation and the borehole stress concentration equation，both the weak-plane shear slip criterion and rock mass Mogi-Coulomb criterions are introduced to build an analysis model for borehole stability.Researches on the reasonable drilling fluid density and safe drilling direction in typical reservoirs show that the existence of bedding plane significantly aggravates the rock damage and changes the damage position on the borehole wall;the collapse pressure of horizontal well continually varies along with the changes of drilling direction，thus the minimum collapse pressure is obtained in a particular drilling direction;in the inclined borehole，the minimum collapse pressure direction acquired is not vertical to the bedding plane experimentally，while the symmetrical inclined boreholes about principal planes have the same fracture pressure in space;the optimum drilling direction is the one with both larger safe density window of drilling fluid and smaller collapse pressure，and the drilling trajectory curve should be controlled strictly in the azimuth where the density window of drilling fluid changes greatly.

bedding;safe density window of drilling fluid;trajectory optimization;borehole stability;model

P634.1

A

1672－7428(2017)03－0001－09

2016－07－19;

2016－09－04

国家自然科学基金项目“考虑热松弛效应的纳米结构材料热弹耦合行为研究”(编号:11472249)、“深孔高温硬岩中涡轮钻进粘滑振动及其抑制机理研究”(编号:41572360);中央高校基本业务费项目“热－力－化多场耦合作用下结晶岩力学特性表征及应用研究”(编号: 2652015080);国家科技支撑项目“农用机井成井设备研制与开发”(编号:2015BAD20B02);国土资源部复杂条件钻采技术重点实验室开放课题“超深孔结晶岩地层热－力耦合井壁稳定研究”(编号:DET201617)

丁立钦，男，汉族，1990年生，山东人，硕士研究生在读，地质工程专业，主要研究方向为与井壁稳定有关的岩石力学问题，北京市海淀区学院路29号，dlq891@163.com。

王志乔，男，汉族，1978年生，室副主任，副教授，博士，长期从事水力压裂及井壁稳定方面的问题研究，北京市海淀区学院路29号，zqwang@cugb.edu.cn。