桥式起重机金属结构的可靠性优化研究

叶青林邢舰艇赵丽华

（1．烟台特种设备检验研究院 烟台 265508）

（2．烟台市技术监督信息研究所 烟台 265508）

桥式起重机金属结构的可靠性优化研究

叶青林1邢舰艇2赵丽华1

（1．烟台特种设备检验研究院 烟台 265508）

（2．烟台市技术监督信息研究所 烟台 265508）

桥式起重机金属结构在设计阶段就需要兼顾轻量化与安全性能要求。以概率模型来简化影响结构可靠性的不确定因素，以可靠度来衡量结构的安全性，建立了桥机金属结构概率可靠性优化的数学模型，获得了兼顾轻量化和可靠性要求的最优解。可靠性优化设计方法既能实现桥式起重机金属结构的轻量化和安全可靠双重目标，是对优化设计方法的进一步创新，并弥补了优化设计的不足，既符合可靠性设计的要求，又能贴合绿色设计的节能环保理念。

桥式起重机 金属结构 可靠性优化 轻量化 安全性

起重机的固有可靠性水平是在设计阶段决定的，设计阶段是决定其是否安全的第一步，也是最重要的一步。如果设计的起重机结构可靠性水平不高，无论后天的管理、维修、保养水平多高，产品还是不安全的。桥式起重机作为常见的特种设备，其金属结构的故障较为频繁，稍有不慎极容易酿成重大事故，在设计阶段需要考虑可靠性要求；金属结构的质量约占整台起重机质量的60%～80%[1-2]，实现轻量化设计具有突出意义；现阶段，设计人员一般采用手工试凑法，做起重机金属结构设计时出于安全考虑，在校核强度、刚度和稳定性时一般会留有一定的设计裕度，而常规的优化设计为追求结构轻量化往往把强度、刚度和稳定性等许用值用到极限，这样做不能确保结构是否安全，其最优设计方案一般不会被起重机企业所采纳[3]。本文以概率模型来简化影响结构可靠性的不确定因素，以可靠度来衡量结构的安全性，建立桥机金属结构概率可靠性优化设计数学模型，探究了一种既能实现轻量化又能兼顾结构安全的可靠性优化方法。该方法可在设计阶段就能确定结构的固有可靠性，弥补了常规优化设计的不足，既符合可靠性设计的要求，又能贴合绿色设计的节能环保理念。

1 可靠性分析模型简化

1.1 不确定因素及其分布统计

影响桥机金属结构可靠性的不确定因素主要包括起升载荷、材料力学性能、几何尺寸的随机性因素[4-5]，并可以用概率模型来简化。定义影响桥机金属结构可靠性的基本随机变量：

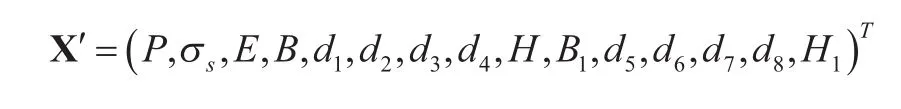
●1.1.1 起升载荷的随机性模型

起升载荷可认为近似服从正态分布，见式（1）：

式中：

μP、σP——起升载荷均值与标准差；

PQ——额定起升载荷。

●1.1.2 材料相关参数的随机性

1）材料的屈服极限。

在进行可靠性分析时，一般需要进行大量实验来估计材料屈服极限的分布，如果无法进行试验，可认为材料的屈服极限值近似服从正态分布，即：均值变异系数VS= 0.07[6]。

2）材料的弹性模量。

●1.1.3 主、端梁截面几何尺寸的随机性

如图1所示，金属结构主、端梁截面主要包括以下12个变量：主梁翼缘板宽度B、主梁上翼缘板厚度d1、主梁下翼缘板厚度d2、主梁主腹板厚度d3、主梁副腹板厚度d4、主梁腹板高度H、端梁翼缘板宽度B1、端梁上翼缘板厚度d5、端梁下翼缘板厚度d6、端梁左腹板厚度d7、端梁右腹板厚度d8、端梁腹板高度H1。

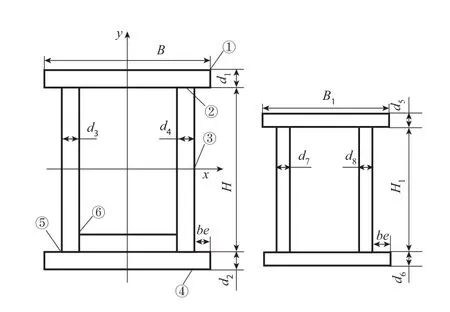
图1 主梁、端梁截面简图

工程应用中大部分钢板使用负偏差，有些负偏差甚至达到公称厚度的7%[7]。为了研究方便，以正态分布来简化主梁和端梁截面几何尺寸d1～d8的分布规律，设钢板厚度的公称尺寸为δ，上偏差为0，下偏差为Δδ，根据“3σ”原则，板厚的均值标准差Sδ= Δδ/6 。

一般认为由加工制造引起截面尺寸B，H，B1，H1的随机性也服从正态分布，按照“3σ”原则，根据上、下偏差可计算出几何尺寸的最大值xmax和最小值xmin，然后均值和标准差Sx分别按式（2）、式（3）计算：

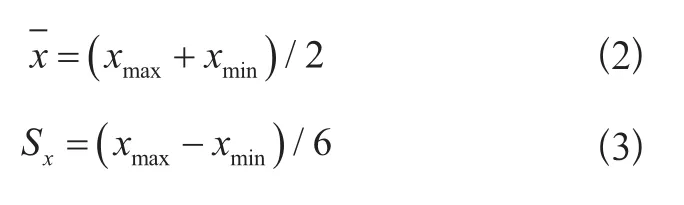
1.2 桥式起重机结构主要失效模式

根据桥架主梁和端梁承受的载荷特点，提出桥机金属结构系统强度、刚度、稳定性失效准则，根据失效准则可以确定相应的失效模式。设满载小车在主梁跨中产生的垂直弯矩为Mx、水平弯矩为My，主梁的垂直截面惯性矩Ix，水平截面惯性矩Iy，第i（i=1，2，3…）个验算点的横坐标xi，纵坐标yi。

1）主梁静强度失效准则：主梁危险截面验算点①、②、③、④处超过许用值，则认为失效，极限状态方程分别为：

①点处应力：

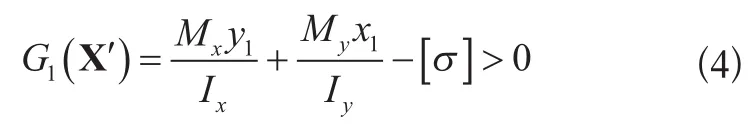
②点处应力：

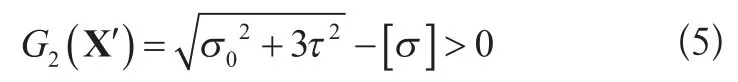
式中：

σ0——水平弯矩与竖直弯矩在②点产生的弯曲正应力；

τ ——腹板上边缘的切应力。

③点处应力：

式中：

Fc1——腹板上的垂直剪切力；

Tn——水平惯性力引起的扭矩；

hd——主梁跨端处腹板高度；

A0——主梁跨端截面面积。

④点处应力：

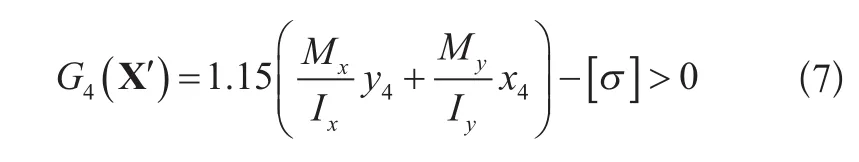
2）主梁疲劳强度失效准则：主梁危险点⑤、⑥处应力超过材料疲劳应力许用值，则认为失效，极限状态方程分别为：

⑤点处应力：

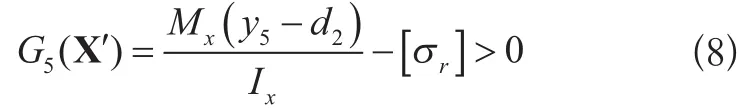
式中：

⑥点处应力：

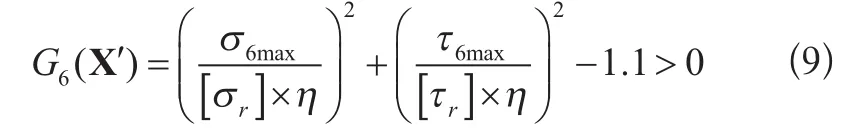
式中：

σ6max、τ6max——载荷组合A计算的大隔板下端与腹

板连接处焊缝的拉应力和切应力。

3）主梁刚度失效准则：主梁跨中满载静位移达到许用静挠度，或满载自振频率未达到自振频率控制值，则认为失效，极限状态方程分别为：

（1）静刚度失效：

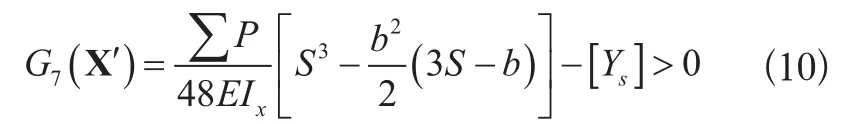
式中：

ΣP ——移动集中载荷之和；

S、b ——桥架跨度、小车轮距；

（2）垂直动刚度失效：

式中：

y0——额定起升载荷点产生的静位移；

λ0——额定起升载荷对钢丝绳产生的静位移；

β ——结构质量影响系数。

4）主梁稳定性失效：主梁的高宽比超过3，则认为失效，其极限状态方程为：

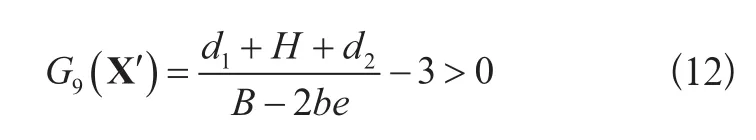
5）端梁强度失效：端梁危险截面1-1、2-2、3-3（如图2所示）应力超过许用值，则认为失效。

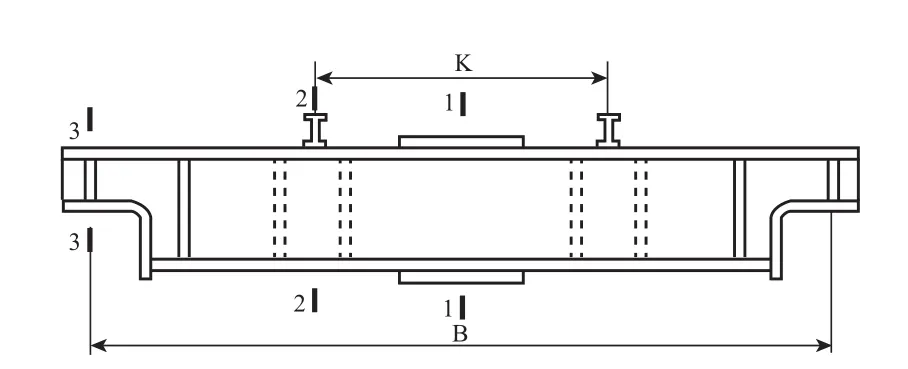
图2 端梁危险截面示意图

1-1截面应力：

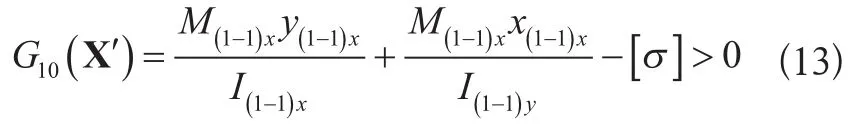
式中：

M(1-1)x、M(1-1)y——垂直载荷与水平载荷在截面1-1角点处产生的弯矩。

2-2截面应力：

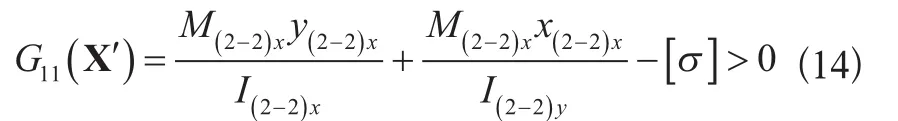
式中：

M(2-2)x、M(2-2)y——垂直载荷与水平载荷在2-2截面角点处产生的弯矩。

3-3截面应力：

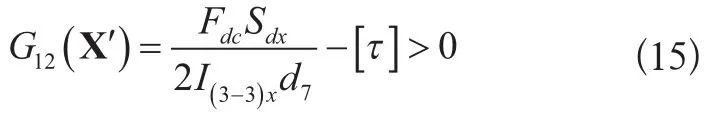
式中：

Fdc——截面3-3垂直剪切力；

Sdx——验算点以上截面对x轴的静距。

6）端梁稳定性失效准则：端梁高宽比超过3，则认为失效，其极限状态方程为：

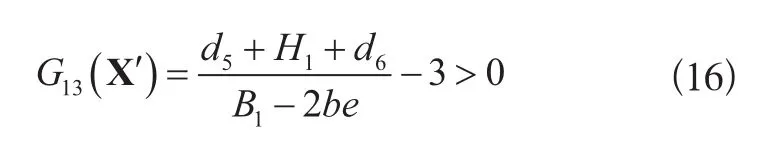
桥机金属结构各失效模式间式（3）～式（16）是“或门”关系，即任何一个失效模式的出现均会引起桥机金属结构的失效。

1.3 桥式起重机金属结构可靠性分析方法

由式（3）～式（16）可知，各失效模式的极限状态方程大都是隐式的非线性函数。此外，极限状态方程之间含有部分相同的随机变量，这导致各极限状态方程）之间存在相关性。因此，很难获取结构系统所有失效模式的联合概率密度函数，直接积分法计算结构系统可靠度的方法是不可行的。蒙特卡洛数值模拟法对各失效模式是否相关以及极限状态方程是否为非线性隐式的形式都没有要求，是一种被公认的相对精确且简单通用的可靠性分析方法[8-9]。

2 可靠性优化数学模型的建立

可靠性优化实现了常规优化设计与可靠性分析理论的结合，是基于可靠性的优化设计，能够实现轻量化与安全性双重目标。具体做法为：将常规优化设计定量变成服从一定分布的随机变量，将强度、刚度和稳定性等确定型约束变成可靠性约束。

2.1 概率可靠性优化随机设计变量

2.2 概率可靠性优化约束条件

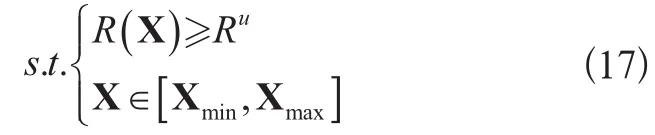
式中：

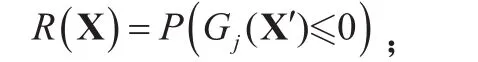
Rμ——结构目标可靠度值；

Gj——桥机金属结构的第j个失效模式的极限状态函数；

Χmin、Χmax——随机设计变量Χ的上、下边界值组成的向量。

2.3 概率可靠性优化目标函数

以桥机金属结构的重量作为目标函数，对于双梁桥机金属结构，可按下式计算：

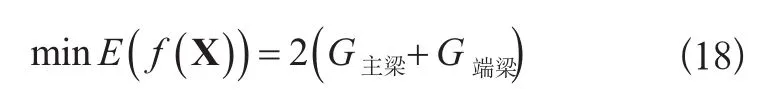
式中：

G主梁、G端梁——单根主梁、端梁的重量。

3 工程实例应用

3.1 实例一

以80t/28m（E7） 中 轨 双 梁 通 用 桥 式起重机金属结构为研究对象，基本随机变量各参

数均服从正态分布。其中：起升载荷均值E(Q ) = 64t，标准差σ(Q ) =0.3×E(Q ) = 19.2t；结构材料为Q235，屈服极限均值标准差Sσ= 18.095MPa；抗弯弹性模量均值标准差SE= 6.18×103MPa；钢板厚度d1，d2，d3，d4，d5，d6，d7，d8正偏差取0，负偏差取0．5mm；截面参数B，H，B1，H1正偏差取5mm，负偏差取5mm。

基于MATLAB软件进行优化计算，优化算法采用能够求解约束优化问题的改进粒子群算法[10-11]。基于蒙特卡洛法，目标可靠度分别取0．9、0．99、0．999，进行概率可靠性优化，并与原手工设计法设计方案、常规优化设计的最优解进行对比，详见表1，并绘制变化曲线如图3所示。

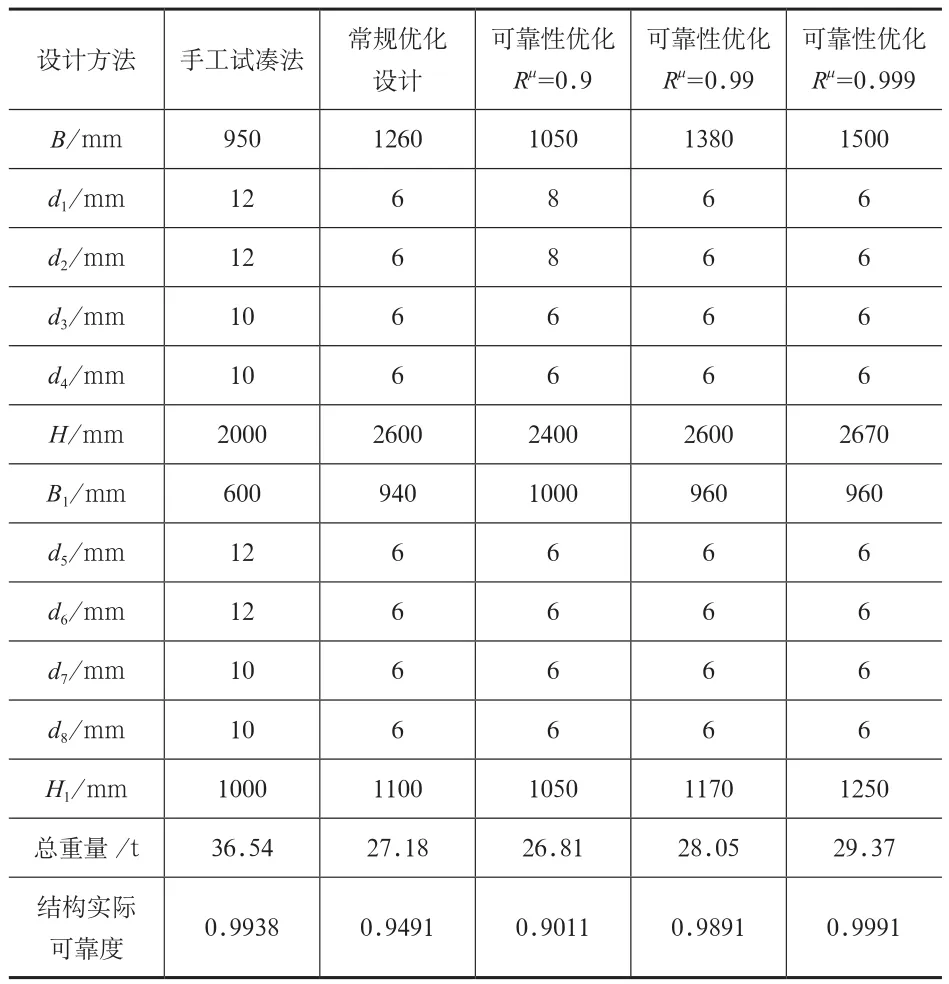
表1 80t/28m（E7）基于三种设计方法的设计方案对比

图3 80t/28m（E7）基于三种设计方法的设计方案对比图

3.2 实例二

以50t/37．5m（E5） 中 轨 双 梁 通 用 桥 式起重机金属结构为研究对象，基本随机变量各参数均服从正态分布，其中：起升载荷均值E(Q ) = 25t，标准差σ(Q ) =0.5×E(Q ) = 12.5t；其他参数与实例分析一相同。

基于蒙特卡洛法，目标可靠度分别取0．9、0．99、0．999，进行概率可靠性优化，并与原手工设计法设计方案、常规优化设计的最优解进行对比，详见表2，并绘制变化曲线如图4所示。

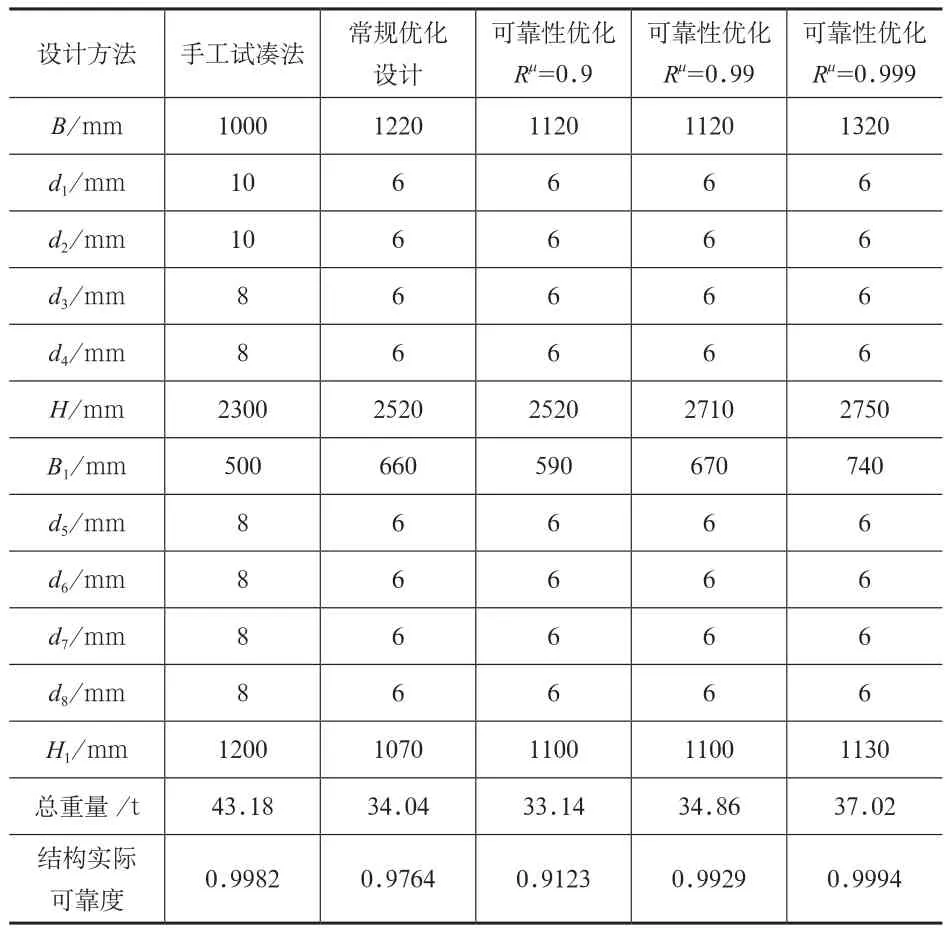
表2 50t/37.5m（E5）基于三种设计方法的设计方案对比

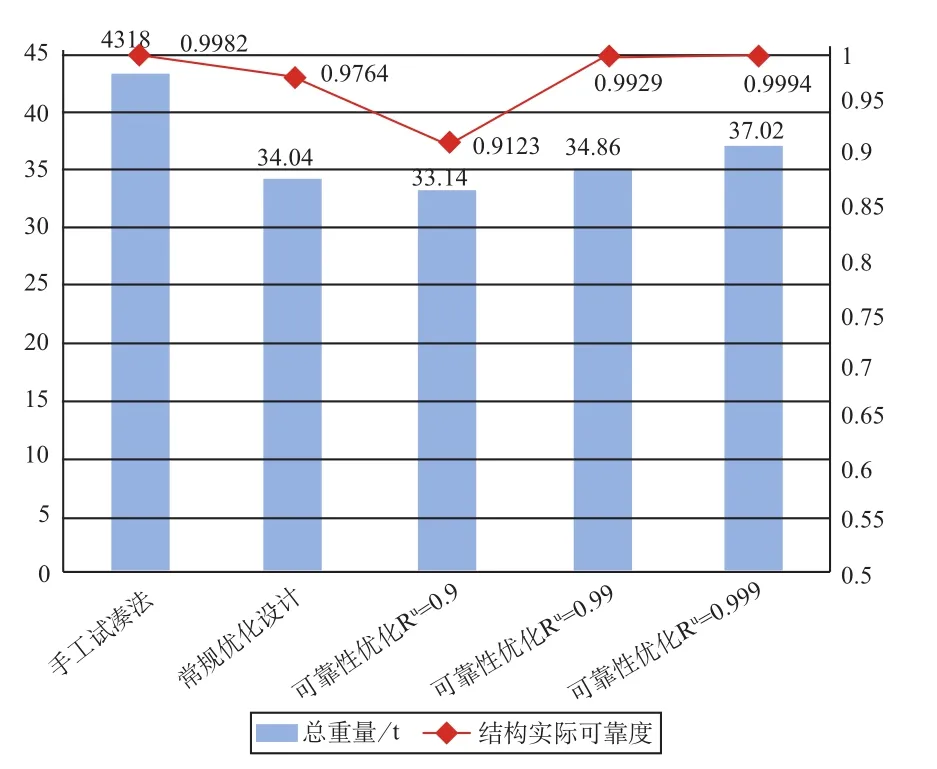
图4 75t/37.5m（E5）基于三种设计方法的设计方案对比图

3.3 实例分析

表1和表2中数据结合图3与图4的对比图，可发现：

1）传统的手工试凑法获得的设计方案一般具有较高的可靠度，即安全性较高，但获得的设计方案没有满足轻量化要求，一般不是最佳的设计方案，仍有改进的余地；

2）常规优化设计方法的设计方案能够满足轻量化的要求，但结构的可靠度达不到令人满意的效果，即不具备较高的安全性；

3）可靠性优化设计的方案能够兼顾结构轻量化与安全可靠性能要求。

4 结论

桥式起重机金属结构的可靠性优化设计方法既能满足轻量化要求、实现节能减排，又能兼顾结构的安全性要求、获得较高固有可靠性的金属结构设计方案。可靠性优化方法优于传统的手工试凑法和常规优化设计，为桥式起重机金属结构的设计开辟了一条新的方法，并且该方法是对现有结构优化设计方法的进一步创新，弥补了常规优化设计的不足，既符合可靠性设计的要求，又能贴合绿色设计的节能环保理念。

[1] 徐格宁．机械装备金属结构设计[M]．北京：机械工业出版社，2009.

[2] 张质文，虞和谦，王金诺．起重机设计手册[M]．北京：中国铁道出版社，2013：75-77.

[3] Hee Youb Kang，Byung Man Kwak．Application of maximum entropy principle for reliability-based design optimization[J]．Structural and Multidisciplinary Optimization，2009，38(4)：331-346.

[4] 张义民，孙志礼．机械产品的可靠性大纲[J]．机械工程学报，2014，(14)：14-20.

[5] 张义民，张雷．基于神经网络的结构可靠性优化设计[J]．应用力学学报，2005，22(1)：49-54.

[6] 闻邦椿．机械设计手册[M]．北京：机械工业出版社，2010：4150-4170.

[7] 喻颖．起重机械制造用钢板负偏差问题的探讨[J]．起重运输机械，2012，(03)：98-100.

[8] 安伟光，赵维涛，安海．随机结构系统综合有静强度、刚度和疲劳的多失效模式的可靠性分析[J]．中国科学，2009，37(4)：516-526.

[9] 唐家银，何平，赵永翔，等．应力-强度相关性干涉下的随机安全系数与零件可靠性设计[J]．机械设计与制造，2011，(12)：16-20.

[10] 叶青林，陶元芳．粒子群算法结合惩罚函数用于桥式起重机主梁优化[J]．起重运输机械，2015，(4)：46-49.

[11] Yuanfang Tao，Chaofei Hong．User-oriented and visualized optimization for crane design[C]．Proceedings of China Modern Logistics Engineering: Inheritance，Wisdom，Innovation and Cooperation，2015：209-216.

Reliability-based Optimization for Overhead Traveling Crane Metal Structure

Ye Qinglin1Xing Jianting2Zhao Lihua1
(1. Yantai Special Equipment Inspection and Research Institute Yantai 265508)
(2. Yantai Technical Supervision Information Research Institute Yantai 265508)

In the design of overhead traveling crane metal structure, lightweight and reliability requirements need to be considered all together. Based on probabilistic model to describe the uncertain factors of the structure, and the reliability to measure the structural safety, mathematical model of probabilistic reliability-based optimization design is established, and then the optimization solution with the requirement of lightweight and reliability is obtained. As the further innovation of the conventional optimization, reliability-based optimization realized both structural lightweight and safety, which makes up for the deficiency of the conventional optimization. Reliability-based optimization for overhead traveling crane metal structure not only meets the requirements of reliability design, but also fts the concept of green design for energy-saving and environmental protection.

Overhead traveling crane Metal structure Reliability-based optimization Lightweight Security

X941

B

1673-257X（2017）03-0032-05

10．3969/j．issn．1673-257X．2017．03．006

叶青林(1989～)，男，硕士，检验员，从事电梯、起重机械、场内机动车辆的研究工作。

2016-09-01）