六自由度双臂机器人动力学分析与运动控制

吴 俊

(1.北方工业大学计算机学院，北京 100144；2.大规模流数据集成与分析技术北京市重点实验室，北京 100144)

六自由度双臂机器人动力学分析与运动控制

吴 俊1,2

(1.北方工业大学计算机学院，北京 100144；2.大规模流数据集成与分析技术北京市重点实验室，北京 100144)

人形机器人运动过程中稳定持物是机器人领域的一个关键研究内容，作为人形机器人中的重要研究方向，六自由度双臂机器人合作抓持重物的稳定性和安全性难以保证。通过对机器人持物运动过程中的受力和运动分析，提出了基于配置构型评估和动力学分析的控制方法，有效解决了持物过程中的稳定性问题。通过对轨迹点的局部最优调整抓取姿态，利用双臂操作过程中受力分析，借助典型的LuGre摩擦模型，构建摩擦力和滑动接触数理模型，并进行动力学分析，在此基础上，提出了相应的控制方法。通过数值仿真，验证了在此控制方法下六自由度双臂能够平稳有效的持物运动。

六自由度；双臂机器人；抓取质量评估；LuGre摩擦；动力学分析

0 引言

在家用和工业机器人繁荣发展的今天，人类对机器人的需求也更加多样。其中双臂机器人包络抓取在工业、救援、看护、军事等方面有着越来越广泛的需求。双臂抓取是一种利用多关节表面操作一个物体的一种操作，在人形机器人研究领域受到广泛关注。之前的很多研究人员用具有很多自由度的连杆来实现对物体的操作，但却很容易由于外界的干扰和故障而失败。相比而言，用多个机械臂包围抓取一个物体即包络抓取，却能在保证操作稳定性和健壮性的同时抓取更大更重的物体，它能通过把重力分散到各个接触点从而减小关节所需的驱动力，而且在很多情况下，包络抓取是唯一的解决办法。尽管有很多优点，由于“包络抓取”在操作中接触点不停在变的这一特性，可能会导致抓取不稳定而不能抵抗外力的影响。

文献[1][2]中用了多种方式来评估抓取质量，得到每个位置的最佳抓取配置构型，但由于实验对象较轻而并没有重点考虑动力学特征，使运动的不可靠性增加。Kazuki Tamura等人对机器臂抓取圆柱形物体受力与运动进行了分析与研究，利用LuGre摩擦模型对双臂和目标物体之间接触点的摩擦动力学进行建模[3]，但仅针对平面二自由度。

基于以上问题和研究现状。为使六自由度双臂完成抱球情况下的轨迹运动，提出了以抓取质量评估和动力学建模为基础的控制方法，从全局和局部分别考虑了如何达到预期的效果，在全局的角度，有了路径之后，分别计算选取了整个路径上每一点（路径点密度相关）的最优配置构型。在局部的角度，为了从初始条件到达每一步，需要通过动力学模型的解算来求出关节力矩的表达式，然后通过比例增益的方法以得到合适的力矩，从而驱动每一步。

第二部分讲述了如何选取合适的配置构型，第三部分是动力学模型的解算，第四部分根据第二部分和第三部分的内容提出了控制算法并给出数理仿真与实验结果分析。第五部分总结。

1 配置构型的选取和抓取效果评估

配置构型即抓取矩阵的计算依赖于物体的重心位置、各个接触点位置、基坐标、各个关节的位移和承重，具体的计算过程参照Domenico Prattichizzo, Jeffrey C.Trinkle在Springer机器人手册中关于抓取的章节[4]。

在计算出每个点的配置构型之后，需要根据抓取质量的评估方法来选出最终的配置构型。在[1][5]中有抓取质量测量方法的广义集合。抓取质量用来评估抓取的效果和抓取稳定性，重力存在的情况下，有两个抓取质量评估方法对于一个稳定的包络抓取至关重要，在这里把它们分别以二分之一的权重相结合以完成配置构型的选取：

（1）最小惯性区域：这里采用的区域选择法的评价标准是使弥补重力和惯性力所需要的力能够最小。典型做法是通过缩小物体重心和抓取中心的距离，其中抓取中心是以接触点为顶点形成的多面体的体心。理想情况是接触力的方向和物体重心方向相交从而能抵消重力和惯性力。

最小惯性区域是物体表面的某些部分，这些部分的摩擦锥包含物体重心。在这些区域的接触点有更强的能力来弥补惯性力。最小惯性区域定义为满足以下条件的点的集合[1][5]，

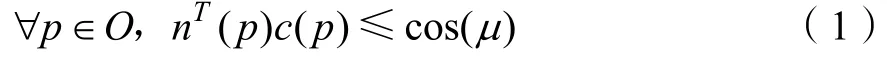
O是物体表面所有点的集合，n(p)是内向物体表面的单位法向量，c(p）是从p指向物体重心Cm的单位中心向量，μ是摩擦系数。

（2）重力补偿系数

为了减小抓取和操作物体所需的力矩，尽可能的减小物体所受到的内力是很有必要的。在与环境没有任何碰撞的情况下，物体所受到的最大的外力是重力，若能使接触点法向量与重力反向，则会非常有利。为了这个目的，定义了以下的抓取质量评估方法：

g是重力的单位向量。理想的情况是当接触点法向重合于重力时，关节应用很小的力矩就能抵消重力的作用，此时此项系数为零。

（3）最终抓取排名和配置构型选择：分两步完成理想接触点和理想配置构型的选择：第一步，假设物体一开始放在理想的位置，在物体表面，通过前一个接触点的相邻位置找到最小惯性区域。然而，考虑到双臂机器人自由度较少，有可能没有可行的配置构型包含这个接触点。因此，需要通过求解逆运动学，从而在最小惯性区域内找到包含此接触点的可行的配置构型。值得注意的是，在实时应用场景中，由于以矩阵为运算单位，计算量大，为了减少计算时间，可以根据时间限制减少每一步的候选配置构型数。第二步，所有通过第一步评估的配置构型将进行重力补偿系数的评估。最终综合上述两个指数定义了全局质量评估指数：

qi和 qi,init分q别是评估指数和初始值，Wi是权重参数。根据两个质量评估方式的权值确定了最终的全局质量指数（需要正规化），这个指数是最终选择合适构型的基础。

2 动力学分析

在选取了每个位置较优的配置构型后，需要合适的力驱动双臂使整体达到相应的配置构型并完成每一步的运动。这里采用经典的拉格朗日动力学分析方法分析来解决系统的动力学问题。

2.1 六自由度双臂系统

图1展示了抱有球形物体的六自由度双臂系统的实体建模和坐标设置。

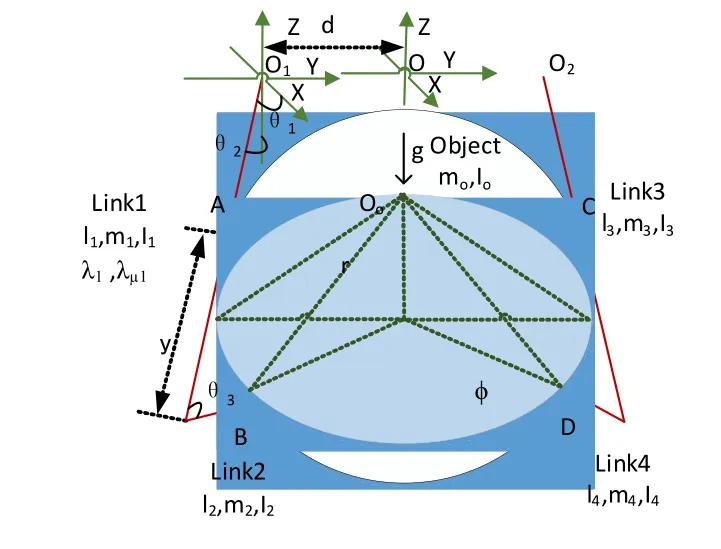
图1 抱球六自由度双臂系统Fig.1 6-DOF dual-arm with a ball

假设以下条件成立：

（1）机器人两个手臂都由2个刚性连杆和3个活动关节；

（2）把刚性球作为大而重的物体来考虑；

（3）在两个手臂上的4个接触点考虑静态和动态摩擦力；

（4）机器人关节摩擦力忽略不计；

假定抱定的物体是质量均匀的球体，所以两个手臂同步一致。

各个记号的定义如下：

l1和l2分别是连杆1、3和2、4的长度,m1，m2和m0分别是连杆1、3，连杆2、4和物体的质量,I1,I2和I0是关节1、3，关节2、4和物体的转动惯量，r是物体的半径。

依据机器人在关节空间中的动力学方程封闭形式的一般结构式。它反映了关节力或力矩与关节变量、速度和加速度之间的函数关系。机器人的运动方程和带有静态和动态摩擦力的系统的动力学建模如下：

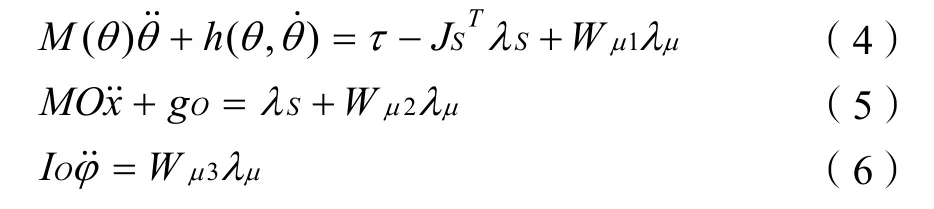
简要的表示为：

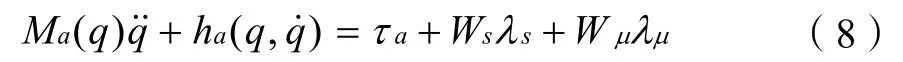
2.2 静态和动态摩擦力分析

这里采用LuGre摩擦模型，该模型用两个接触面间弹性刚毛的平均偏移来表征摩擦力的动态行为。接触点的静态和动态摩擦力定义为以下单一的等式[5][6]。产生的摩擦力用以下式子计算：

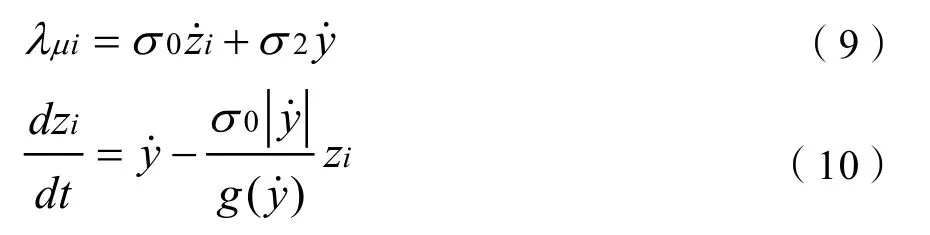
σ0和σ1分别是刚毛的刚性和弹性，σ2是流体粘性摩擦系数，z是平均刚毛形变，y是机器人手臂的肘与接触点之间的距离，y˙是机器人相对于物体的滑动速度。下标i（=1，2）表示是linki的变量。速度无关函数。

FC和FS分别是库仑摩擦力和静态摩擦力。参数vs是Stribeck速度，决定了g(y˙)以多快的速度接近FC。当y˙（滑动速度）很快时，摩擦力收敛到FC，相反则收敛到FS。

四个接触点 A, B, C, D选取A, B分析，其余两点相似，则A,B相对于原点O可以表示为：

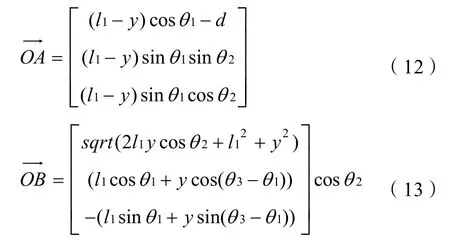
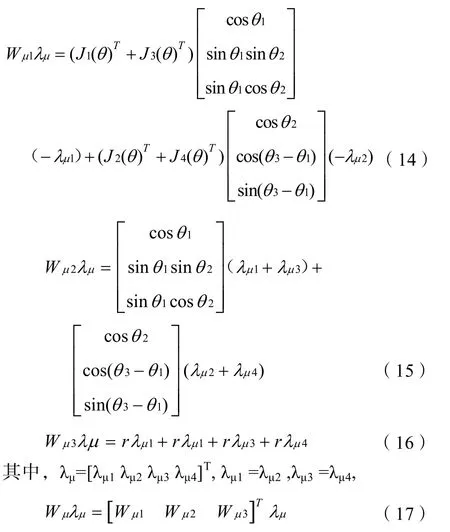
2.3 接触力分析

接下来重点描述滑动接触的细节，球心也就是

其中Bz是接触点 B的 z轴坐标，又有 r/y=tan(θ/2)所以y=r/tan(θ/2)代入上式并对其关于时间求导数，能够得到

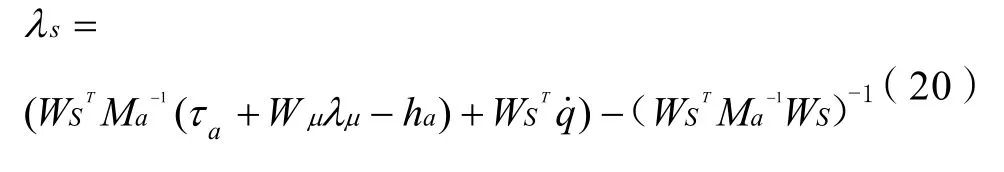
3 控制算法与数理仿真

3.1 控制算法

通常，静态和动态摩擦是不能实时计算的，这一点对于进行数值仿真是很重要的。控制算法如下：

第一步：路径和抓取姿态选取

1）给出理想的路径。在目标路径上选择 m个离散点作为子目标，子目标之间的连接形成了对数理路径的模拟逼近，m的大小取决于路径跟踪的精度。

2）基于物体在每一点的位置信息，通过求解逆运动学，得到相应点可靠的配置构型。

第二步：动力学模型解算

2）把计算出来的Wμμλ作为外力带入式（8），并通过式（24）计算接触力（完整约束力）向量 Sλ 。

3）利用 Sλ 和Wμμλ 计算角加速度矢量

其中τ是控制输入。

第三步：控制输入

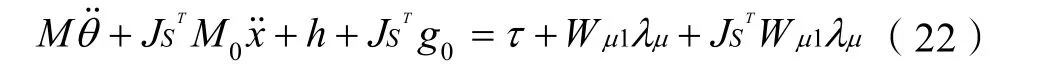
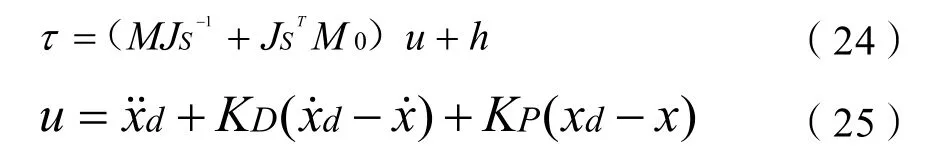
其中xd是理想轨迹，并且KD∈R2X2, KP∈R2X2两者分别是导数和比例增益矩阵。

3.2 参数设置与仿真

在路径的离散点上找出相应的离散点，并找到相应位置最佳的配置构型，得到相应位置的抓取矩阵，假设摩擦系数µ1=µ2=µ3=µ4=0.1，理想路径是[0.3+0.11cos((2π/T)t)-0.1+0.11 sin((2π/T)t)],系统的其它参数包括l1=l2=0.5 m, m1=m2=10.0 kg ,m0=20.0 kg,其中与 LuGre摩擦模型相关的参数设定为 σ0= 5000 N/m，σ1=632 kg/s,σ2=0.0 kg/s，υs=0.001 m/s, 综合质量抓取方法中的ϖ1=ϖ2=1/2。

利用matlab完成了仿真实验，图2和图3分别展示了当KD=30I2,KP=225.0I 2和当KP=50I2的情况下抓取物体的重心运动轨迹曲线，可以看出采用这里提出的控制方法在两种参数设置下走出的实际运动曲线都很接近理想曲线从而证明具有很好的稳定性。

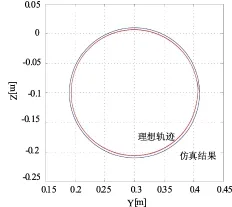
图2 KP=225.0I2效果图Fig.2 The effect picture when KP=225.0I2

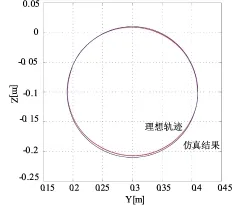
图3 KP=50I2效果图Fig.3 The effect picture when KP=50I2

4 结论

首先分析了针对本系统运动过程中的最佳抓取位姿信息，然后详细分析了六自由度双臂操作系统的动力学特征，其中利用了LuGre摩擦模型对复杂的摩擦力进行分析，最后进行了数理仿真验证了基于抓取f质量和动力学分析控制方法的有效性。

未来将针对控制力矩的输入做更多的研究，并将动力学分析应用到自由度更灵活的系统上。

[1]Behzad Talaei, Farzaneh Abdollahi, H.A.Talebi.Whole Arm Manipulation Planning Based on Grasp Dynamic Properties and Sampling-Based Algorithms with Kinematic Analysis[C]//20th Iranian Conference on Electrical Engineering (ICEE2012), Tehran, Iran: IEEE, 2012: 963-968.

[2]R.Suarez, M.Roa, and J.Comella.Grasp quality measures[R], Technical Report, Technical University of Catalonia, 2006.

[3]Kazuki Tamura, Fumihiko Asano.Whole Arm Manipulation with Effects of Static and Dynamic Friction on Body Surface[C]//11th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI).Kuala Lumpur, Malaysia: IEEE, 2014: 273-278.

[4]Bruno Siciliano Prof., Oussama Khatib Prof.Springer Handbook of Robotics.Springer Berlin Heidelberg.2008: 671-702.

[5]B.Talaei, H.A.Talebi, F.Abdollahi.Whole arm manipulation planning and control[D].M.Sc.thesis.Tehran, Iran: Department of Electrical Engineering, Amirkabir University of Technology, 2012.

[6]Anderson DO, Moore JB.Optimal filtering[M].Prentice-Hall; 1979.

[7]M.Ding, R.Ikeura, T.Mukai, H.Nakashima, S.Hirano, K.Matsuo, M.Sun, C.Jiang and S.Hosoe.Comfort estimation during lift-up using nursing care robot-RIBA[C]//Proc.of the First Int.Conf.on Innovative Engineering Systems.Alexandria, Egypt: IEEE, 2012:246-250.

[8]D.Prattichizzo and J.C.Trinkle.Springer Handbook of Robotics: Chapter 28, Grasping[M], pp.647-669, 2006.

[9]Anderson DO, Moore JB.Optimal filtering [M].Prentice-Hall; 1979.

[10]D.Hoshino, M.Izutsu, N.Kamamichi and J.Ishikawa.Friction compensation control based on the LuGre model[C].JSME Conference on Robotics and Mechatronics: No.11-5.Okayama, Japan, 2011: 2A2-K08 (1)-2A2-K08 (4).

[11]K.J.Astrom, C.Canudas De Wit.Revisiting the LuGre friction model[J].IEEE Control Systems Magazine, 2008, 28(6): 101-114.

[12]Li Y, Tong S, Li T.Adaptive fuzzy output feedback control for a single-link flexible robot manipulator driven DC motor via backstepping[J].Nonlinear Analysis Real World Applications, 2013, 14(1): 483-494.

[13]Dimaio SP, Salcudean SE.Optimal selection of manipulator impedance for contact tasks[C]//Proceedings of IEEE international conference on robotics and automation, 2004, 5: 4795-4801.

Dynamic Analysis and Grasp Control Method of 6-DOF Dual-arm Robot

WU Jun1,2
(1.College of Computer Science and Technology, North China University of Technology, 100144; 2.Beijing Key Laboratory on Integration and Analysis of Large-scale Stream Data)

Steady grasp of humanoid robot under motion conditions is a key research field.As a new research direction of humanoid robot, the steady and secure grasp of huge and weight object of 6-DOF dual-arm robot is still difficult to guarantee.With the analysis of load and motion in the grasp process, proposed a new method based on configuration evaluation and kinematic analysis, using force analysis and conventional LuGre friction model, built model of friction and sliding friction, using kinematic analysis, based on all above, new control method proposed.It was verified that using the method, the 6-DOF dual-arm’s grasping option can be stable and effective.

6-DOF; Dual-arm robot; Grasp quality evaluation; LuGre friction; Dynamics analysis

TP24

A

10.3969/j.issn.1003-6970.2017.03.026

吴俊(1993)，男，硕士，研究生，主要从事分布式系统，多机器人系统。

本文著录格式：吴俊.六自由度双臂机器人动力学分析与运动控制[J].软件，2017，38（3）：128-132