电网异常条件下的DFIG转子位置观测器

赵梅花，杨奎民，林立，杨勇

(1.洛阳理工学院 电气工程与自动化学院，河南 洛阳，471023；2.邵阳学院 多电源地区电网运行与控制湖南省重点实验室，湖南 邵阳，422000；3.苏州大学 城市轨道交通学院，江苏 苏州，215137；)

电网异常条件下的DFIG转子位置观测器

赵梅花1，杨奎民1，林立2，杨勇3

(1.洛阳理工学院 电气工程与自动化学院，河南 洛阳，471023；2.邵阳学院 多电源地区电网运行与控制湖南省重点实验室，湖南 邵阳，422000；3.苏州大学 城市轨道交通学院，江苏 苏州，215137；)

论文根据双馈感应发电机(DFIG)在电网异常条件下的数学模型，提出一种滞环转子位置观测器来获得转子位置角。该观测器的实现主要依据实际转子电流和估算转子电流正序分量的相位偏差，采用滞环控制器来调节估算转子位置。此观测器结构简单，无需调节任何参数，实现方便；所提出的观测器既适应于理想电网条件下DFIG的运行控制，也适用于电网异常情况下DFIG的故障穿越运行。搭建了双馈风力发电系统仿真模型，对提出的控制策略进行仿真验证。仿真结果验证了所提方案的可行性和正确性。

双馈感应发电机；电网异常；无度传感器；滞环转子位置观测器

双馈感应发电机(Doubly-fed induction generator,DFIG)因能实现变速恒频运行，在风力发电系统中备受关注。在该系统中，DFIG定子直接与电网相连，转子通过双PWM变换器进行交流励磁，实现DFIG输出有功和无功功率的解耦控制。

DFIG控制策略的研究要用到转子位置角θr。θr可通过速度传感器获得[1]，也可采用无速度传感器控制技术获取[2]。无速度传感器技术无需安装和维护转子位置传感器，系统成本低，可靠性高，适应于在恶劣环境下工作。因此，无速度传感器控制在双馈风力发电中的应用越来越受到国内外学者的重视。文献[3-5]提出基于转子电流的模型参考自适应(Model Reference Adaptive System，MRAS)转子位置观测器，采用PI调节器作为自适应控制器。该观测器的估算精度受PI参数和电机参数影响；上述文献均在αβ坐标系下用定子磁链估算转子电流，定子磁链的估算误差将直接影响转子电流的估算精度。现有的双馈风力发电系统无速度传感器技术的研究成果均适合于理想电网条件下DFIG的运行控制，对于电网异常条件下转子位置观测器的研究尚未看到相关文献。

本文提出一种不平衡电网电压条件下基于滞环控制(Hysteresis control,HC)的转子位置观测器。此观测器依据实际转子电流和估算转子电流正序分量相位偏差估算转子位置。为避免文献[12-13]中采用定子磁链观测器估算转子电流所带来的估算误差，所提出的观测器在正转同步旋转dqP坐标系下用定子电压和电流的正序分量直接估算转子电流正序分量，提高了电流估算精度。仿真研究验证了所提策略的可行性和正确性。

1 电网电压不平衡条件下DFIG的等效模型

定子按发电惯例、转子按电动惯例。DFIG在同步旋转坐标系下电压和磁链矢量方程为

(1)

(2)

下标“+”表示正序分量，“-”表示负序分量，“s”表示定子，“r”表示转子，上标“P”表示正转，“N”表示反转；us,ur,is,ir,ψs,ψr分别为定子、转子电压、电流及磁链矢量；Lm,Ls,Lr分别为定、转子同轴等效绕组间的互感、定子等效两相绕组的自感和转子等效两相绕组的自感；ω1为电网电压同步旋转角频率，ωr为转子旋转角频率，ωslip+=ω1-ωr为正转转差角频率。

DFIG正转同步坐标系下等效电路如图1所示，其中Lσs,Lσr为定、转子漏感。

图1 正同步旋转坐标系中DFIG等效电路Fig.1 The equivalent circuit of DFIG in positive synchronous rotating coordinate

2 基于转子电流的转子位置估算原理

2.1 dq坐标系下转子电流正序分量估算模型

(3)

由式(2)与式(3)可得

(4)

将式(4)改写为正负序分量可得

(5)

由式(5)估算转子电流时，包含转子电流负序二倍频分量，可采用二阶陷波器滤除二倍频分量，二阶陷波器传递函数为：

(6)

式中ω0=2ω1=200πrad/s为截止频率；ξ为衰减系数。实际系统中考虑到滤波效果和控制系统稳定性，取ξ=0.707。二阶陷波器伯德图2所示。

图2 二阶陷波器伯德图Fig.2 The bode diagram of the second order notch filter

由上图可知，在频率为2ω1附近，其增益很小，可以滤除二倍频的负序分量。式(5)经二次陷波器分离出转子电流在dqP坐标系下的正序分量为

(7)

(8)

将式(8)代入式(7)中得

(9)

(10)

图3 转子电流估算模型

图3中的PLL为电网电压锁相环。

2.2 转子位置偏差函数εr的构建

(11)

在dqP坐标系下，εr的模表示为：

(12)

3 滞环转子位置观测器

图4 HC观测器结构Fig.4 Schematic of observer based on the HC controller

图5 HC原理图Fig.5 The diagram of hysteresis controller

图5中，H为滞环宽度。本文选取几个不同的H值进行仿真，对仿真结果进行分析，得出最佳滞环宽度为H=0。H=0时的滞环控制规律为

(13)

4 电网电压不平衡条件下HC观测器仿真

本文采用Matlab仿真技术验证提出的HC转子位置观测器在电网故障条件下实现的正确性和可行性。

仿真时转子侧变换器及DFIG控制策略采用电网电压不平衡条件下的PIR矢量控制策略[6]，基于滞环转子位置观测器的DFIG PIR矢量控制结构如图7所示。

图7 电网不平衡条件下DFIG PIR矢量控制策略框图Fig.7 The PIR control strategy of DFIG unbalanced network conditions

仿真时DFIG并网线电压为270V。仿真条件为：①电网电压单相跌落25%，故障发生时段为[0.6s 1.2s]；②DFIG风电机组运行转速为1000r/min；③定子输出平均有功、无功功率参考分别为2800W和0Var;网侧变换器直流母线电压200V。仿真波形如图8～9所示。

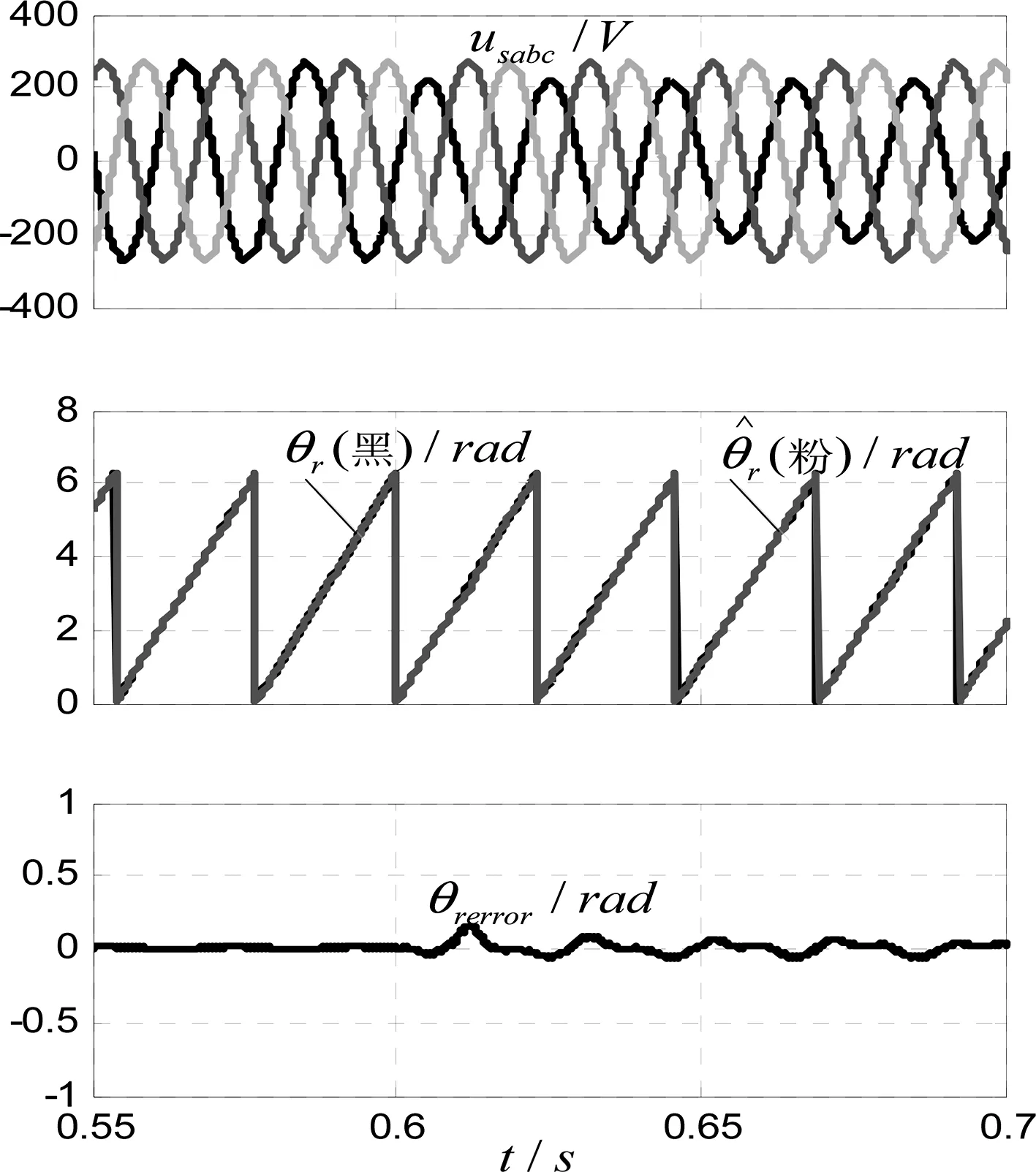
图8 单相跌落25%实际与估算转子位置仿真波形Fig.8 Simulation waveform of the actual and estimated rotor position with 25% of single-phase voltage drop

图9 电网电压单相跌落25%时DFIG主要物理量仿真波形Fig.9 Simulation waveform of DFIG with 25% of single-phase voltage drop

图9为电网电压下不平衡条件下基于HC转子位置观测器的DFIG PIR控制策略仿真波形。由图9可知，在故障发生的整个时段[0.6s 1.2s]内，在基于HC转子位置观测器的DFIG PIR策略控制下，DFIG定子电流和转子电流正弦度好、平衡度高，定子输出功率Ps,Qs和电磁转矩Te均在允许的误差范围内可控。

仿真验证了所提出的HC转子位置观测器在电网发生故障时能正确估算转子位置；基于HC转子位置观测器的DFIG PIR矢量控制策略具有良好的故障穿越能力。

5 结 论

本文对提出适合电网电压不平衡条件下的HC转子位置观测器进行了分析和讨论。通过仿真研究验证了在电网电压不平衡条件下，HC观测器均能准确估算转子位置。

[1]刘其辉,王志明.双馈式变速恒频风力发电机的无功功率机制及特性研究[J].中国电机工程学报，2011(3):82-89.

[2]康忠健，吕学志，陈天立，等.基于转子电流的模型参考自适应模糊控制双馈风力发电机转子位置观测器设计[J].电力系统保护与控制,2010,38(21):72-82.

[3]Monhammed O，Liu Z,Liu S.A novel sensorless control strategy of doubly fed induction motor and its examination with the physical modeling of machines[J].IEEE Trans on Magnetics,2005,41(5):1852-1855.

[4]Marcetic D P,Vukosavic S N.Speed-sensorless AC drives with the rotor time constant parameter update[J].IEEE Trans on Industrial Electronics,2007,54(5):2618-2625.

[5]高乐,周有庆,徐隆亚,等.基于转子电流的双馈感应电机无速度传感器控制[J].电力系统自动化，2010,34(13):61-65.

[6]Hu Jia bing,He Yikang,XuLie,et al.Improved control of DFIG system during network unbalance using PI-R current regulators[J].IEEE transactions On Industrial Electronics,2009,56(2);439-451.

The rotor position observer design of DFIG under unbalanced network conditions

ZHAO Meihua1，YANG Kuimin1，LIN Li2，YANG Yong3

(1.Luoyang Institute of Science and Technology,Luoyang 471023，China；2.Shaoyang University，Hunan Provincial Key Laboratory of Grids Operation and Control on Multi-Power Sources Area，Shaoyang 422000，China；3.School of Urban Rail Transportation,Soochow University,Suzhou 215137，China)

A hysteresis rotor position observer was presented to acquire the rotor position angle based on mathematical model of the doubly-fed induction generator(DFIG)under unbalanced network conditions.The observer estimated the rotor position and speed by hysteresis controller to adjust the phase deviation between actual rotor current and estimated positive sequence component of the rotor current,the system structure is relatively simple,without adjusting any parameters,easy to achieve.Simulation model for wind energy generation system-with DFIG is set up.The simulation results show that the control strategy is feasible and efficient.

doubly-fed induction generator;unbalanced network conditions;sensorless;rotor position hysteresis observer.

1672-7010(2017)01-0076-06

2016-09-12

国家自然科学基金青年基金项目(51407124);.河南省高等学校重点科研项目(16A470012);湖南省科技计划项目(2016TP1023);湖南省教育厅科学研究重点项目(16A191)

赵梅花(1966-)，女，河南西平人，副教授，博士，从事新型电力电子变换及新能源发电技术研究；E-mail:zhaomh2013@126.com

TM46 < class="emphasis_bold">文献标志码：A

A