一类n阶常微分方程的周期边值问题

刘兴元,张亚平

(邵阳学院 理学与信息科学系，湖南 邵阳，422000)

一类n阶常微分方程的周期边值问题

刘兴元,张亚平

(邵阳学院 理学与信息科学系，湖南 邵阳，422000)

本文利用Mawhin延拓定理研究一类n阶常微分方程的周期边值问题，获得了其解存在的充分条件。

n阶常微分方程；周期边值问题；存在性；充分条件

对于二、三阶常微分方程的周期边值问题，已有许多研究,见文献[1-10],使用的方法是Banch空间中锥拉伸、压缩定理以及上、下解方法。

对于n(n≥4)阶微分方程的周期边值问题的研究相对较少，仅见文献[11-15]，在文[12]中研究了周期边值问题

(1)

获得了(1)存在正解的充分条件。

文[11]研究了一类奇周期边值问题

(2)

建立其解的存在准则。

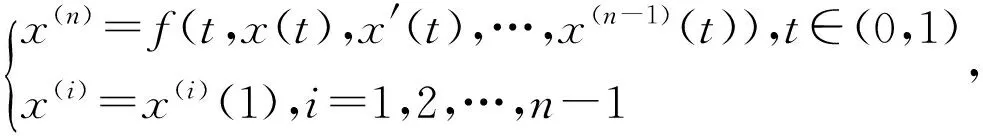
(3)

这里f:[0,1]×Rn→R是连续函数，n≥1是一个整数，我们的目的是建立问题(3)存在解的充分条件。本文所有符号若没特别说明，均参见文献[4]。

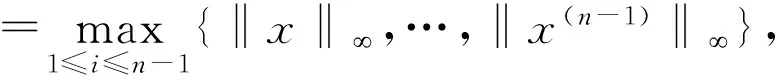
分别定义线性算子L和非线性算子N如下

L:X∩domL→Y,Lx(t)=x(n)(t),x∈X∩domL

N:X→Y,Nx(t)=f(t,x(t),x′(t),…,x(n-1)(t)),x∈X

其中L的定义域domL={x∈Cn[0,1],x(i)(0)=x(i)(1),i=0,1,…,n-1}。

1 几个引理

为了证明下列定理，先给出几个引理

引理1[4]下面的结论成立

(ⅰ)KerL={x(t)≡c,t∈[0,1],c∈R};

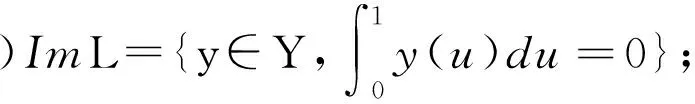
(ⅲ)L是零指标Fredholm算子；

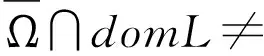
(ⅴ)x(t)是问题(3)的解当且仅且x是算子方程Lx=Nx在domL上的解。

(ⅰ)Lx≠λNx，其中(x,λ)∈[(domLKerL)∩∂Ω]×(0,1);

(ⅱ)对任意x∈KerL∩∂Ω,有Nx∉ImL;

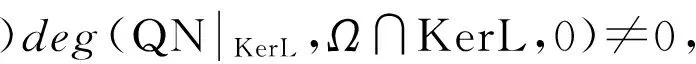
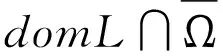
2 本文主要定理及证明

定理1 假设下面的条件成立

(A1)存在连续函数e(t)和非负连续函数gi(t,x)(i=1,2,…,n-1)，使得f满足

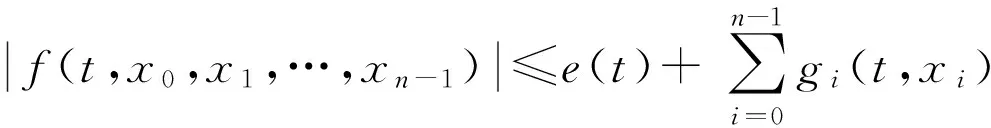
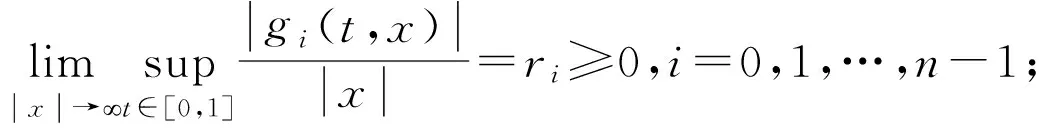
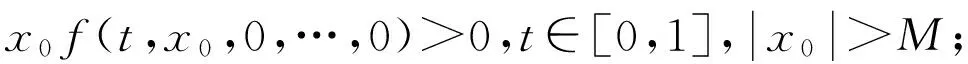
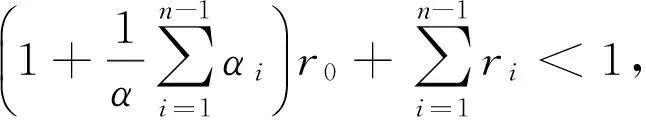
(4)

则问题(3)至少有一个解。

证明 第一步 令Ω1={x∈domL/KerL,Lx=λNx,λ∈(0,1)}，对于x∈Ω1,容易看出存在ξi∈[0,1],使得x(i)(ξi)=0,i=1,…,n，于是

……………

(5)

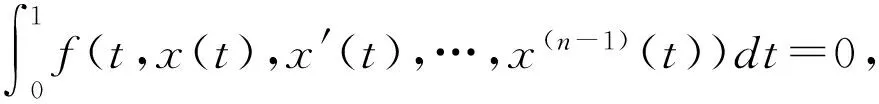
从而

(6)

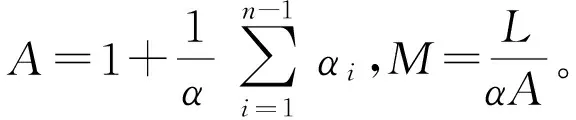
x(n)(t)=λf(t,x(t),x′(t),…,x(n-1)(t))，

(7)

对上式从ξn-1到t积分，并使用(A1)，可得

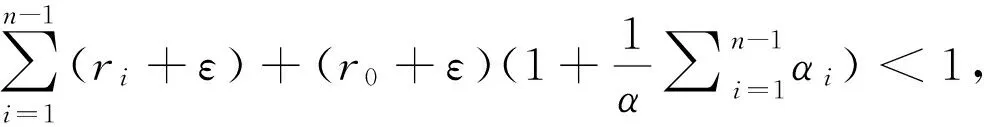
对于i=0,1,…,n-1，记

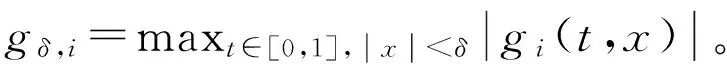
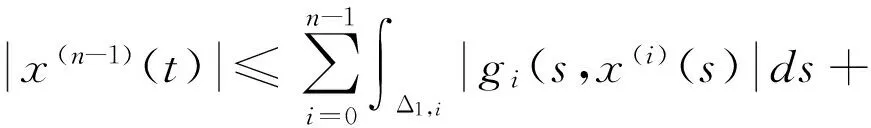
应用(5)和(6)式有

‖e‖‖e‖。

因此

‖x(n-1)‖

‖x(n-1)‖+

(r0+ε)A(M+‖x(n-1)‖)+‖e‖。

第二步 令Ω2={x∈KerL,Nx∈ImL}，设x∈Ω2,则x(t)=c∈R,

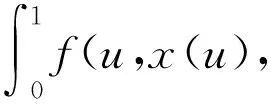
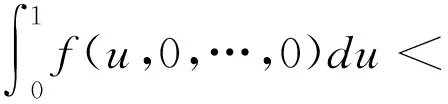
第三步 令Ω3={x∈KerL,λΛx+(1-λ)QNx=0,λ∈[0,1]}，其中Λ∶Y/ImL→KerL

设xn(t)=cn∈Ω3,而且当n→时，则有数列λn∈[0,1]使得

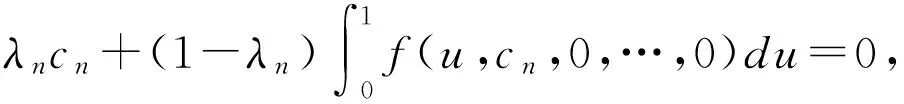
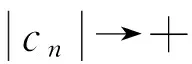
若cn→+，则对充分大的n有cn>M；应用(A2)，有0，矛盾。

若cn→-，则对充分大的n有cn<-M；应用(A2)，有0，矛盾,故Ω3有界。

(a)对任意的x∈(domL/KerL)∩∂Ω,λ∈(0,1)有Lx≠λNx；即引理2中条件(i)成立；

(b)对任意x∈KerL∩∂Ω,有Nx∉ImL，即引理2中条件(ii)成立。

事实上，令H(x,λ)=λΛx+(1-λ)QNx，

其中Λ:Y/ImL→KerL

按Ω的定义知道对于x∈∂Ω∩KerL,有H(x,λ)≠0，由度的同伦性有

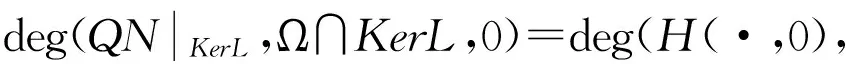
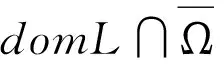
定理2 设下列条件成立

(B1)定理1中的(A1),(A2)成立；

(B2)存在常数M>0，使得问题

(8)

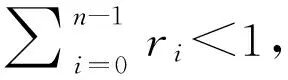
证明：令Ω1={x∈domL/KerL,Lx=λNx,λ∈(0,1)}，对于x∈Ω1,我们得到

x(n)(t)=λf(t,x(t),x′(t),…,x(n-1)(t))。

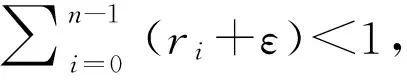
这样

于是，存在常数H>0，使得‖x(n-1)‖≤H,从而‖x‖≤M+H。证明的余下部分与定理1的相对应的部分完全相同，略。

例 考查周期边值问题

(9)

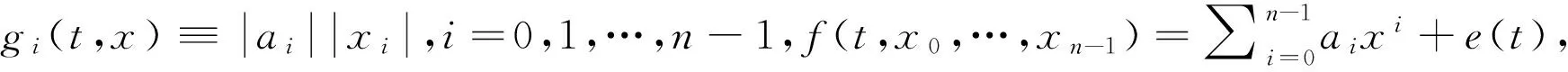
将上三式与定理1对照比较知定理1中的条件(A1)，(A2)，(A3)成立，由定理1知

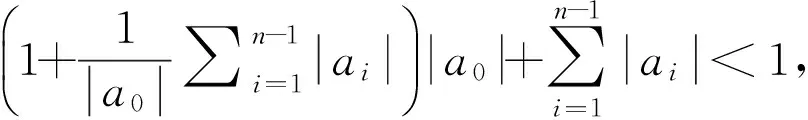
[1]Agarwal R P.Boundary value problems for higher order differential equations[M].Word Singapore：Scientific,1986.

[2]Agarwal R P.Focal boundary value problems for differential and differential equations[M].London：Kluwer academic publishers，1998.

[3]Agarwal R P，O’Regan D,Wong P J Y.Positive solutions of differential,difference and integral equations[M]. Dordrecht：Kluwer Academic Publishers,1999.

[4]郭大均,孙经先,刘兆理.非线性常微分方程泛函方法[M].济南：山东科学技术出版社,1995.

[5]钟承奎,范先令,陈文原.非线性泛函分析引论[M].兰州:兰州大学出版社,1998.

[6]Rachunkova I.Existence of two positive solutions of a singular periodic boundary value problems[J].J.comput.Appl.Math,2000,113:27-34.

[7]Rachunkova I.On the existence of more positive solutions of periodic boundary value problems with singularity[J].Appl.Anal,2001,79:257-275.

[8]Yang X.Upper and lower solutions for periodic problems[J].Appl.Math.Comput,2003,137:413-422.

[9]Kong L,Wang S,Wang J.Positive solutions of singular nonlinear third-order periodic boundary value problem[J].J.Comput.Appl.Math,2001,132:247-253.

[10]Li Y.Positive solutions of fourth-order periodic boundary value problems[J].Nonl.Anal,2003,54:1069-1078.

[11]Njoku F I，Omari P,Singularly perturbed higher order periodic boundary value problem[J].J.Math.Anal.Appl,2004,289:639-675.

[12]Cabada A.The methods of lower and upper solutions periodic boundary value problems[J].J.Math.Anal.Appl,1995,195:568-589.

[13]刘雪琴,黄永奎,裴明鹤.一类n阶常微分方程周期边值问题的可解性[J].北华大学学报(自然科学版),2013,14(2):22-27.

[14]刘兴元,具p算子方程非齐次混合型二阶微分方程多点边值问题[J].邵阳学院学报(自然科学版),2013,10(2):1-4.

[15刘兴元.具p-laplacica 算子的混合边值问题正解的存在性[J].邵阳学院学报(自然科学版)，2010,7(02),6-10．

Existence of solutions for periodic boundary problems for n-order ordinary differential equation

LIU Xingyuan，ZHANG Yaping

(Department of Science and Information Science,Shaoyang University,Shaoyang 422000,China)

In this paper,usingMawhinextension theorem,we discuss the existence of periodic boundary value problems forn-order ordinary differential equation,we obtain some several sufficient conditions.

n-order ordinary differential equation;periodic boundary value problem;existence;sufficient condition

1672-7010(2017)01-0010-06

2016-11-01

湖南省教育厅一般项目(12C0864)

刘兴元(1963-)，男，湖南邵阳人，教授，从事常微分方程边值问题研究

O175.1 < class="emphasis_bold">文献标志码：A

A