“分数的基本性质”教材比较研究

◇葛素儿

分数的基本性质在分数教学中占有重要的地位，在小学数学学习中起着承前启后的作用。它既以分数的意义、分数的大小比较为基础，又与整数除法及商不变的性质有着内在的联系，更是分数约分、通分的依据，也是进一步学习分数加法和减法计算、比的基本性质的基础。教材提供了怎样的教学思路呢？我们对现在使用的人教版、浙教版、北师大版、苏教版、青岛版和西师大版等六套教材进行梳理与分析，并由此作出思考。

一、六套教材引入部分学习素材的比较

学习素材决定学习活动，不同的学习素材预示着不同的教学路径，会产生不同的教学效果。我们对六套教材的引入部分进行比较，得出以下结论：在“分数的基本性质”的编排上，传统教材突出的是“结果”和“计算”，现行教材则“重视过程和体验”。

解读这些教材，共性之处在于：

1.尊重学生的朴素经验，注重直观图的应用，基于“寻找相等分数”展开观察与操作，注重学生的过程体验。

不同之处在于：

1.北师大版教材的相关教学安排在五年级上学期进行，其他教材均安排在五年级下学期。

2.人教版、浙教版和苏教版教材通过学生的动手操作引入，在涂一涂、折一折等活动中发现分子、分母的变化规律（如图1）。而北师大版、青岛版和西师大版教材则直接从观察入手，引导学生发现规律（如图2）。

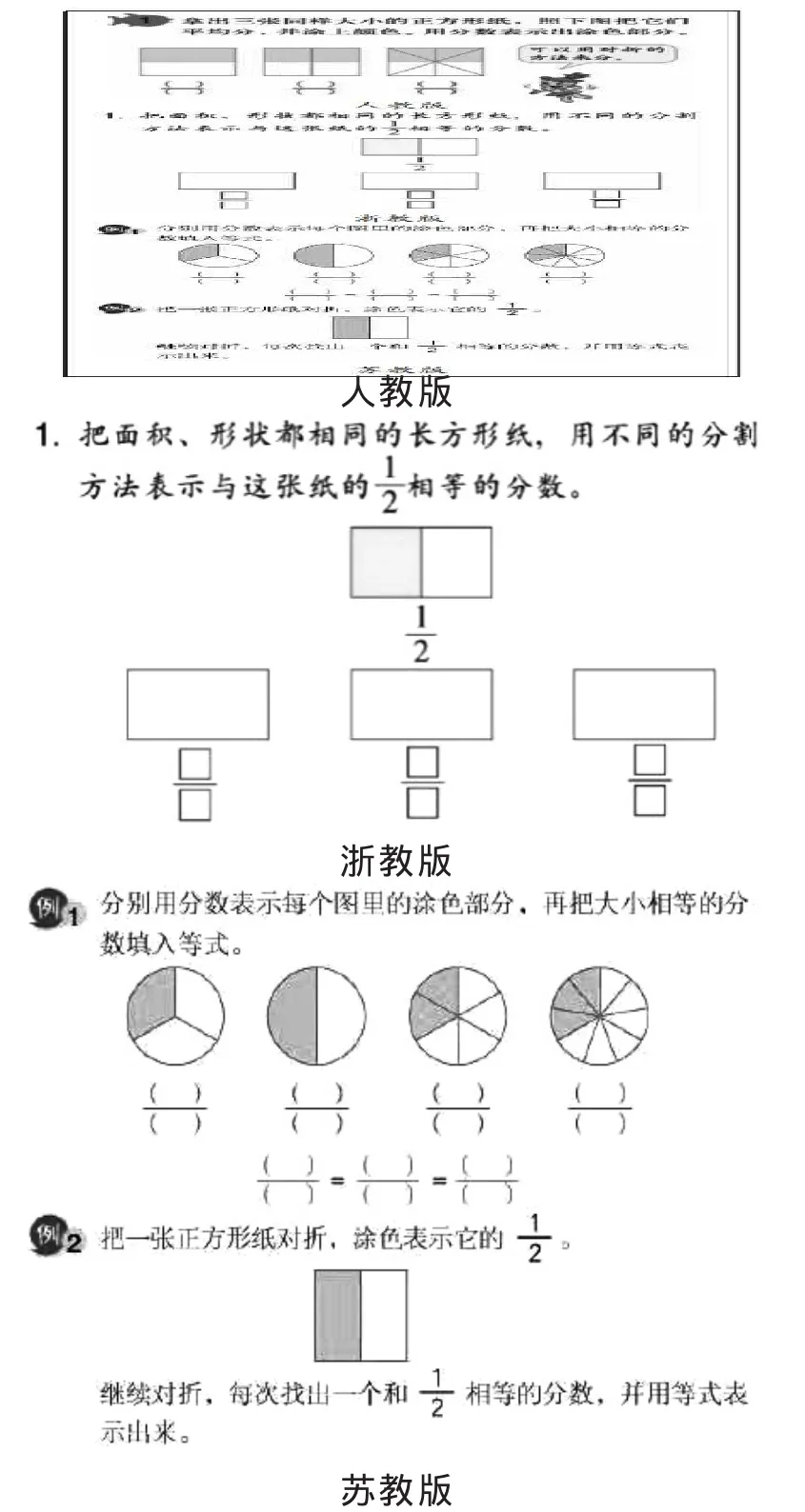
图1

图2

3.从所用个例看，浙教版、苏教版、西师大版教材呈现的分数更丰富些，不仅有分母是2、4、8的相等分数，还有分母是3、6、9、16的相等分数。不同的表达方式、不同类型的数，会让学生对分数基本性质的体会更深刻。

二、六套教材教学路径与核心要素的比较

不同教材提供了不同的学习素材，在活动的设计上也不尽相同，但大体的教学路径基本上是一致的。由此，学生的学习活动大体相同，比如，观察、猜想、验证、发现、概括。对六套教材的教学核心要素进行比较，可得出如下结论：

1.不管哪套教材，都注重直观模型的提供，鼓励学生从直观角度主动地观察和发现，在讨论交流的基础上认识分数的基本性质。其中，浙教版和青岛版教材中出现了数线这样半抽象的线段模型，北师大版教材中出现了抽象的线段模型。

2.各套教材都注重让学生经历知识的形成过程，一般在课堂上都引导学生经历这几个活动：创设情境（现实情境或纯数学情境）发现相等关系→观察分子、分母的变化过程与规律，引发猜想→验证，概括总结结论→知识应用。其中，浙教版教材的设计更为细腻、深刻一些（如图3）。

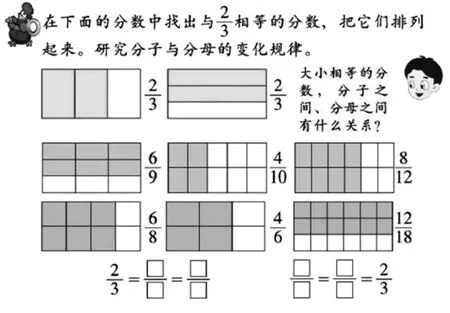
图3

3.分数的基本性质与商不变规律有着密切的联系，以往的教材中是利用商不变的规律，单纯从数的角度学习分数的基本性质。这六套现行教材，无一例外在引入环节回避了商不变性质，都是从几何直观的角度探索分数的基本性质。在得出结论之后，人教版、浙教版和苏教版教材的设计中有与商不变性质问题沟通的环节，其中浙教版教材以“在□中填数”等式变形的方式呈现，而人教版、苏教版教材是以纯问题的形式出现的。

三、由教材对比引发的思考

1.学习方式的选择：注重几何直观。

新课标强调让学生动手实践、自主探索、合作交流，亲历知识的形成过程，各套教材的设计都体现了这一理念，且都凸显了“几何直观”这一元素，体现出它是学习分数的重要方式。因此，“分数的基本性质”的教学一般是以图像为支架的。在教学中，应从儿童的视角出发，以图像为支架，将学习数学知识的过程、方法和结果用图像进行概括，勾勒出将图形、文字、符号等多种数学语言相互转化的视觉学习过程。在北师大版教材中，对引导学生自主表征、表达有着很好的渗透（如图4）。

图4

2.教学难点的突破：聚焦分数单位。

通过前测发现，学生对分数的基本性质知晓率达90%以上（有185名学生认为相等），那么这节课对学生来说是不是就一点难度也没有了？当然不是。“分数的基本性质”是自然数情况下商不变性质的延伸，它的出现引起了分数表示的不唯一性，等值分数的理解与寻找是教学的难点。

分数的基本性质起着“承上启下”的作用，其核心在于“分数单位”。基于“量的守恒”，聚焦分数单位，在“度量”中寻找等值分数，可能会使教学豁然开朗。在这个过程中，一个重要的几何载体即线段模型应发挥作用。浙教版、青岛版及北师大版教材中均出现了半抽象或抽象的线段模型(如图5)。我认为，在新知探究环节，半抽象的数线模型应占据重要的地位；在知识应用环节，抽象的线段模型也应有一席之地。

图5

3.知识体系的建构：合情推理与演绎推理相互印证。

分数的基本性质、商不变性质及比的基本性质，事实上是用不同的形式表示相同的规律，本质相同而形式不同，主要是适应不同的情境。那么，我们如何将分数的基本性质与商不变性质联系起来呢？学生会用什么样的方式联系？老师A就“证明相等”做过一次前测，结果如表1所示。

表1 分数的基本性质前测统计表（单位/人）

在检测中，我们发现仅有2名学生能够和商不变性质联系起来。可见，尽管两条性质本质相同，但要将两者联系起来，对学生来说存在一定的困难。在六套教材的新知探究环节，我们发现它们都放弃了原先从商不变性质引入的做法，而是从直观图示或动手操作入手，在操作、观察、比较中发现相等关系，再通过观察分子、分母的变化规律引发猜想，然后通过验证得出结论。这个过程渗透了不完全归纳的思想，是对学生合情推理能力的培养过程。如果说学生概括分数的基本性质的过程是合情推理的话，那么学生根据分数与除法的关系，以及整数除法中商不变的规律来说明分数的基本性质，则是演绎推理的过程。两种推理相互印证，才能加深学生对分数的基本性质的理解，完成知识体系的建构。这层意思，在人教版和苏教版教材中均有体现。比如，苏教版教材中的问题是：“根据分数和除法的关系，你能用整数除法中商不变的规律来说明分数的基本性质吗？试着在小组里说一说。”但问题在于，学生会如何用商不变性质来说明分数的基本性质呢？我想，浙教版教材的设计可能更符合学生的认知水平（如图6）。

图6

在学习和理解课程标准的基础上，对某一主题的教学内容尽可能多地参考不同版本的教材，这样可以使我们更好地分析、消化和处理教材中的相关学习内容。阅读不同版本的教材对教师而言有一个显而易见的好处，即教师不再把教材神圣化，而是实现了和课程标准的直接“对话”。